> Техника, страница 59 > Магнетооптика

Магнетооптика

Магнет00птика, учение о воздействиях магнитного поля на оптические явления. Попытки обнаружить действия магнитного поля на распространение света в пустом пространстве, производившиеся Фарадеем, и повторяющиеся до последнего времени, давали всегда отрицательный результат. Магнитное поле оказывает однако влияние на процесс излучения и поглощения света и на распространение света в веществе. Таким образом магнетооптич. явления по существу вторичны: магнитное поле изменяет состояние вещества (атомов и молекул), вследствие чего меняются и его оптич. свойства.

Явление Зеемана. Основным магнетооптич. эффектом, к которому в конце концов сводятся все остальные, является зависимость излучаемого и поглощаемого· спектра от наложенного на источник или на поглощающее тело внешнего магнитного поля. С несомненностью это явление впервые было обнаружено в 1896 году Зееманом. Влияние магнитного поля на излучение носит название прямого явления Зеемана, влияние на спектр поглощения называется обратным явлением Зеемана. B первых опытах Зеемана источником света служило натронное пламя, помещаемое между полюсами сильного электромагнита (поле около 10 000 гауссов). Спектр исследовался при помощи большой вогнутой роуландовской диффракционной решетки. Наблюдение производилось перпендикулярно силовым линиям (поперечный эффект) и вдоль силовых линий (продольный эффект). В простейших случаях в поперечном эффекте первоначальная неразложен-ная спектральная линия с частотой колебаний V распадается на три линии (нормальный триплет), причем частота средней линии остается прежней v, но излучаемый свет линейно поляризован, колебания электрического вектора происходят параллельно полю (фигура 1, где 1—направление поля, 2— неразложенная линия, 3—поперечный эффект, 4—продольный эффект). Две другие линии симметрично смещены от цен-* тральной на расстояние ±Δν, при-

I чем поляризованы так, что колеба-I ² ния электрич. вектора перпендикулярны полю. В поляризационном I I з отношении первый компонент носит s «-* * название π-компонента, а два i i другие «-компонентов. При

i J продольном наблюдении видны толь-

Фиг i ^{ко две линии}> смещенные от первоначального положения на ±Δν, обе линии поляризованы по кругу, причем знак вращения у компонента с положительным смещением +Δν совпадает с вращением тока, образующего магнитное поле. Разложение линий указанного типа (т. наз. н о р-мальный эффект Зеемана) наблюдается в немногих исключительных случаях т. наз. сингулетных линий. Обычно результат разложения значительно сложнее (аномальный эффект Зеемана).

Теория нормального эффекта на основании классическей электронной теории дана Лоренцом. Пусть электрон с зарядом е и массою т, колеблющийся в атоме, помещен в однородное магнитное поле Н. Выберем ось Ζ параллельно Н. Компоненты магнитных сил, действующих на электрон, согласно законам электродинамики будут:

^=-сft^H’ ^Fy=-cTt^H> ω

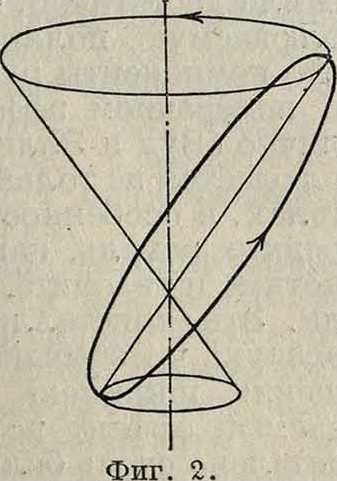
τ. е. перпендикулярны как направлению компонента скорости, так и полю. Силы такого рода в первом приближении вызовут вращательное прецессионное движение всей системы (например электронной орбиты) вокруг оси, параллельной полю и проходящей через ядро атома (фигура 2); направление вращения, если смотреть по направлению силовых линий, будет происходить против часовой стрелки. Соответствующ. сила Кориолиса, возникающая при вращении осей системы с угловой скоростью и, будет иметь компоненты:

^dx F_z=0. (2)

F_x=2 mu —,

F_y=— 2mu

dt

Сравнивая (1) и (2), находим u=H, куда число об/ск.

ω=~^~Н.

от-

(3)

Любое эллиптич. движение электрона можно разложить на одно линейное колебание, параллельное полю, и на два круговых с вращением вправо и влево в плоскости, поперечной полю. Из ур-ия (1) ясно, что первая слагающая не испытает никаких изменений в магнитном поле, но будет излучать свет линейно поляризованный, с колебаниями параллельно полю вдоль силовых линий, то есть при продольном наблюдении этот компонент не может давать излучения. Частота двух круговых колебаний изменится соответственно на ± ώ, причем при поперечном наблюдении (при рассматривании круговых колебаний в профиль) излучаемый свет будет линейно поляризован с колебаниями, поперечными полю. Так как со=и Δω=— ,^с2 ΔΑ, то изменение длины волны в нормальном явлении Зеемана должно иметь величину

ΔΛ=± ^Л2 -, - ^е-Н. (4)

- - Алтс² ni ^{ν 7}

Соотношение (4) точно подтверждается на опыте для случая нормального триплета. При наблюдении вдоль поля, согласно изложенной теории, будут наблюдаться только два измененных круговых колебания в соответствии с опытом.

Полная физич. теория как нормального, так и аномального явления Зеемана дается на основе теории квантов (смотрите). По основному постулату теории квантов частота излучаемой или поглощаемой спектральной линии определяется условием-Бора:

Еа Е

^ν=Τ~Ύ’ ©

где Е{, Е_к—энергии стационарных состояний атома и h—универсальная квантовая постоянная. Появление новых линий в магнитном поле м. б. истолковано только как

Е-h

ном поле. Изменение частот Αν должно равняться изменению термов:

Av=^-^=Av_i-Av_1{. Щ

Возьмем случай движения электрона по эллипсу; по второму постулату теории Бора (смотрите Кванты) момент количества I движения для этого случая должен равняться

Ah ВИШИ.·

_2π, где j—целое число 0, 1, 2, 3. Для эллиптической орбиты

I=mm sin (v, г)=~,

где ν—орбитальная скорость электрона, г— радиус-вектор, проведенный от ядра к электрону. Вследствие прецессии электронной орбиты в магнитном поле возникнет добавочная энергия вращения:

АЕ=2πω·Ι cos (I, Η)=2πα>) ~ cos (I, Η), τ. e.

Δν=^Δ®= ω) cos (I, Η). (V)

Опыт показывает, что в реальном газе с беспорядочно расположенными орбитами, следовательно и векторами 1, при разложении в магнитном поле, получаются совершенно отчетливые компоненты; это значит, что

) cos (J,H)=m _ (8),

не может иметь любых значений от —j до +)

*13

(в противном случае получилось бы не расщепление, а размытие спектральной линии). В связи с этим возникает необходимость ввести новое квантовое число, называемое магнитным или экваториальным; оно определяет прерывность возможных пространственных положений орбиты в магнитном поле. По определению т (8) видно, что оно может принимать ряд целых значений, лежащих между j и—j, всего следовательно 2j + 1 значений. Из (6) следует таким образом, что

. Δν=ω(»Β,· — т_к), (9)

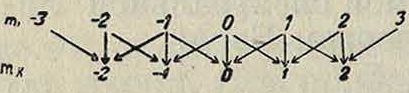
причем ω имеет значение (3), вытекающее из классич. теории. Для выяснения поляризации и интенсивности компонентов разложения в теории Бора необходимо установить соответствие с классич. теорией. Такой принцип соответствия приводит к следующим выводам: возможные значения изменения магнитного квантового числа должны удовлетворять условию Ат=+1 или 0; случай Ат=0 соответствует π-компонентам, случай Δт=± 1—а-компонентам. Эти «правила отбора», вытекающие из принципа соответствия, ограничивают число компонентов, возможных по формуле (9), и приводят к нормальному триплету. В виде примера возьмем случай, когда квантовое число j в начальном состоянии достигает значения 3, а в конечном 2, тогда возможные значения магнитных квантовых чисел т_г и т_к будут определены согласно фигура 3, но между ними будут комбинироваться и давать компоненты расщепления только пары, связанные стрелками, согласно вышеуказанному правилу. Получается всего 15 компонентов, однако, поскольку разности m,· — m_k=± 1 или 0, они стягиваются в нормальный триплет, то есть получается тот же результат, что и в классич. теории. Причиною такого совпадения является предположенное в формуле (9) тождество со как в начальном, так и в конечном состоянии. Более глубокий анализ магнитных условий в атоме показывает, что такое тождество возможно только в том случае, если магнитный момент внешних электронов в атоме компенсируется собственным магнитным моментом вращающихся вокруг своих осей электронов (электронный «спин»), что достигается для случая так называемым сингулетных спектральных линий (в отличие от муль-типлетных). В общем случае терм

^ЗА^=Д v=mg, (10)

где д—т. наз. «магнитный фактор расщепления». Для нормального явления Зеемана он равен 1, для аномального отличен от 1. По-луэмпирич. теория сложного аномального явления Зеемана развита Ланде, По этой теории, прекрасно совпадающей с опытом,

_п_ j 3 (i 4~ 1) + ^s (^s 4-1) — I (I + 1) ΓΙΉ

У - Г i- ₂j 0 _{+ х)} ·

Здесь s—квантовое число, характеризующее собственное вращение электрона (спин), I—т.наз.побочное квантовое число, соответствующее моменту импульса орбитального движения электрона. В атомной модели д тесно связано с отношением магнитного и механич. момента в атоме. Для общего случая явления Зеемана формула (9) должен быть заменена следующей:

Av=a>(m_ig_i-m_k д_к), (12)

причем попрежнему должен быть соблюдено условие Ат=+1 или 0. Квантовая теория явления Зеемана объясняет ряд эмпирич. закономерностей, наблюдаемых в аномальном эффекте: 1) все члены одной и той же спектральной серии дают одинаковый тип аномального эффекта; 2) гомологическ. линии (то есть полученные при одинаковой комбинации спектральных термов) обнаруживают одинаковый тип расщепления (правило Престона); 3) смещение Αν каждого компонента аномального явления Зеемана находится в простом отношении к смещению в нормальном триплете со, например для линии D₂ натрия Αν=± |со, ³ со, | со (правило Рун-ге); 4) интенсивности компонентов магнитного расщепления находятся также в целочисленных отношениях. ν

В сильных магнитных полях аномальный эффект резко изменяет характер (эффект Пашена-Бака), приближаясь к нормальному триплету с уширенными компонентами, причем смещение перестает быть пропорциональным полю. Это происходит в том случае, когда частота собственной прецессии электронной орбиты становится соизмеримой с частотой прецессии во внешнем магнитном поле; при слабых полях последняя значительно меньше первой. Абсолютная величина смещения в явлении Зеемана незначительна, например для синей линии водорода происходит расщепление на 0,8 А в очень сильном магнитном поле в 45 000 гауссов. Непосредственное спектральное наблюдение эффекта возможно поэтому только с помощью наиболее совершенных диф-фракционных и интерференционных спектроскопов. Явление Зеемана легко обнаруживается однако косвенными оптич. методами, например по влиянию магнитного поля на степень поляризации резонансного излучения ртути; даже слабого магнитного поля земли достаточно, чтобы резко изменить наблюдаемую поляризацию вследствие того, что компоненты расщепления в продольном и поперечном эффекте поляризованы различно (Вуд и Эллит). Явление Зеемана наблюдается не только в газах, но и в твердых телах, в особенности в крист нек-рых редких земель, например в минералах ксе-нотиме и тизоните, содержащих редкие земли. Эти кристаллы дают при ί° жидкого воздуха чрезвычайно тонкие полосы поглощения шириною в несколько А. Наблюдаемый эффект всегда аномальный и относительно очень большой (в^ксенотиме получаются смещения до 10 А при силе поля в 27 000 гауссов).

Явление Фарадея. Исторически первым обнаруженным магнетооптич. эффектом было вращение плоскости поляризации (смотрите) телами, находящимися в магнитном поле. Явление это открыто Фарадеем в 1846 г. Если в поле сильного электромагнита помещать стекло, различные твердые и жидкие прозрачные тела, то, при наб-

Фигура з. людении параллельно магнитным силовым линиям, происходит вращение плоскости поляризации падающего поляризованного света. Между двумя скрещенными николями в отсутствии магнитного поля свет не проходит, при наложении же поля свет проникнет, и для того, чтобы снова получить темноту, окулярный николь придется повернуть на нек-рый угол; этот угол и служит мерою вращения плоскости поляризации. Фарадей нашел, что /_а, на к-рый поворачивается плоскость поляризации, пропорционален силе поля И и длине слоя I, через к-рый проходит параллельный пучок света: a^R-1-Щ (13)

постоянная В (постоянная Верде) зависит от природы вещества, агрегатного состояния, ί° и длины волны. В табл, приведены значения для нек-рых веществ для 3 длин волн.

Значения R для нелоторых веществ.

Вещество	656 Ύημ	589 m/1	486 πιμ
Вода (25°). Сероуглерод (25°). Кварц.	0,0102 0,0319 0,0136	0,0130 0,0415 0,0166	0,0196 0,0667 0,0250
Водород.	0,0430	0,0537	0,0805
Железо. Никель.	217° 92°	195° 75°	145° 64°

Примечания

}при

1=1

УСС.

1=1 сантиметров Н=1 гауссу давлении в 1 atm =1 сантиметров и Н =10 000 га-

! ί=ο,οοι сантиметров Н=15 000 гауссов (насыщение).

Направление поворота плоскости поляризации обычно совпадает с направлением тока, возбуждающего электромагнит. Вследствие того, что направление вращения определяется только направлением поля, знак вращения не меняется, если луч отразить на выходной грани тела и направить обратно, а возрастет вдвое, так как путь I увеличился вдвое. Этим свойством, которого нет у естественных оптических активных тел, Фарадей воспользовался для усиления эффекта, заставляя слегка наклоненный световой луч несколько раз отражаться внутри испытуемого тела до выхода наружу. Явление Фарадея практически безинерцион-но, по измерениям Абрагама и Лемуана оно возникает после наложения поля во всяком случае не позднее, чем через 10~⁸ ск. Попытки применения эффекта для модуляции света в технике наряду с электрооп-тическим эффектом Керра практического успеха до сих пор не имели.

С теоретич. точки зрения явление Фарадея может рассматриваться как необходимое следствие эффекта Зеемана. Факт вращения плоскости поляризации математически эквивалентен тому, что две волны, противоположно поляризованные по кругу, являющиеся синонимом одной плоскополяри-зованной волны, распространяются в среде с различными скоростями, именно:

2πν · I

(14)

где V — частота световых колебаний, с — скорость света в пустоте, μ_± иμ₂—показатели преломления¹ волн, поляризованных по кругу вправо и влево. Скорость света в среде, а следовательно и показатель преломления, определяется по теории диспер сии (смотрите) собственными частотами или линиями поглощения данного вещества. В магнитном поле линии поглощения изменяются, расщепляются, в чем и состоит эффект Зеемана, причем для нормального эффекта (ср. выше) при продольном наблюдении (как это имеет место при магнитном вращении плоскости поляризации) два симметрично смещенных компонента поляризованы по кругу вправо и влево в спектре излучения. В спектре поглощения один компонент будет влиять на скорость распространения волн, поляризованных по кругу вправо, другой на скорость волн, поляризованных по кругу влево, в результате чего с необходимостью по формуле (14) появится вращение плоскости поляризации. Для спектральных областей, далеких от линий поглощения, можно в первом приближении написать:

2}-"+*£· <¹⁵)

где со имеет величину (3) и соответствует частоте прецессии электройной орбиты в магнитном поле. Вставляя (15) и (3) в (4) и переходя от частот ν к длинам волн Я, получаем основную формулу в теории явления Фарадея (ф-ла Беккереля):

^α=2^·^λ·%·^Η· (16)

Формула (16) не только объясняет функциональный вид эмпирического уравнения Фарадея (13), но и позволяет теоретически предвычислять постоянную R, если известна дисперсия вещества,

то есть Полное согласие опыта с формулой (16) получается однако только для газообразного водорода; для остальных веществ правилен только порядок величины вычисляемой постоянной. Определение по опытным данным из ф-лы (16) отношения заряда электрона е к массе т дает для водорода правильную величину 1,75 -10⁷, для воды 1,58-10⁷,для кварца 1,31-10⁷, для бензола 0,99-10⁷ и т. д. Расхождение теории и опыта объясняется тем, что теория развита в предположении газообразной среды, состоящей из атомов, дающих нормальный эффект Зеемана, но для большинства исследованных объектов эти условия не удовлетворяются. Ф-ла (16) выведена на основании приближенного соотношения (15), которое м. б. справедливым только для областей, далеких от полос поглощения. Возможно однако построить более строгую и полную теорию явления (Друде, Фохт, Лоренц и друг.) на основе общей теории дисперсии. От обычной теории дисперсии эта теория отличается тем, что вводится нек-рая внешняя магнитная сила (1), действующая на электрон и вызывающая прецессионное вращение. Получаемые ф-лы в общем случае весьма сложны; соотношения упрощаются для областей, близких к какой-либо определенной линии поглощения. В этом случае с достаточным приближением можно принять:

No e³1Н

Л 2?П²С² (1Y)

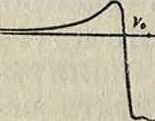
т где N₀ — число диспергирующих электронов, соответствующих данной спектральной линии, μ₀—показатель преломления среды в том случае, если бы в данной спектральной области не находилось линии с частотой ν₀ (практически μ₀—показатель преломления вдали от данной полосы поглощения). Формула (17) показывает, что в области полосы поглощения- по мере приближения к ν₀, а испытывает аномальный ход. На фигуре 4 изображена кривая, показывающая теоретич. измене-•V ние а в области полосы поглощения.Такое аномальное изменение найдено впервые на опыте Макалузо и Корбино и носит название эффекта Макалузо и Корбино. Произвести измерения внутри самой линии (или точнее—дублета расщепления) до сих пор не удалось, в соседних областях теория вполне совпадает с опытом. В последнее время аномальным вращением часто пользуются для определения числа диспергирующих электронов Ν₀, соответствующего данной спектральной линии.

Некоторые растворы и кристаллы редких земель, солей железа и других веществ вращают плоскость поляризации в магнитном поле в направлении противоположном вращению тока, возбуждающего электромагнит. К этой группе относится много парамагнитных тел, почему и самое вращение иногда называют парамагнитным в отличие от обычного магнитного. По Дорфману и Ладенбургу эффект Фарадея определяется, вообще говоря, двумя причинами. Одна из них, на основе которой и построена изложенная теория, сводится к тому, что электронная орбита совершает прецессионное вращение в магнитном поле. Другая состоит в том, что магнитное поле ориентирует атомы благодаря ранее существовавшему в них магнитному моменту. Ориентированные таким образом атомы будут различно реагировать на свет, поляризованный по кругу вправо и влево, и следовательно число электронов, отвечающих на одну и другую волну, будет несколько различным; к этому сводится объяснение парамагнитного вращения. В общей квантовой теории (Френкель) разделение двух факторов, диамагнитного и парамагнитного, строго говоря, является недопустимым; теория в конце концов должна целиком основываться на характере явления Зеемана для данного вещества. Однако для слабых магнитных полей такое разделение целесообразно и в квантовой теории.

Магнетооптическое вращение плоскости поляризации при излучении. Тесно связано с эффектом Зеемана и Фарадея явление, открытое Ган-ле, Вудом и Эллетом в резонансном излучении паров ртути и натрия (смотрите Люминесценция). При возбуждении как поляризованным, так и неполяризованным светом резонансное излучение, рассеиваемое в стороны, также частично поляризовано. При наложении слабого магнитного поля (0.5—10 гауссов) перпендикулярно возбуждающему пучку и электрич. вектору све

товых колебаний можно в направлении поля наблюдать вращение плоскости поляризации излучения и одновременно снижение степени поляризации. Явление объясняется тем, что процесс излучения происходит не мгновенно, но через некоторое время т, соответствующее длительности возбужденного состояния атома (смотрите Люминесценция). Среднее т для паров натрия равно 1,56 ·10~⁸ ск. В магнитном поле атом начинает совершать прецессионное вращение, вследствие чего произойдут зееманов-ское расщепление линий и эффект Фарадея. По формуле (3) можно рассчитать период прецессии; для поля в 1 гаусс этот период равен 7)5· 10^-7 ск., для 10 гауссов 7,5-10^-8 ск. Т. о. за один период прецессии возбужденный атом успеет значительно повернуться, прежде чем он излучит квант; ориентировка его станет иная и плоскость поляризации излучаемого света повернется. При этом т величина статистическая, различная для разных атомов, вследствие чего отдельные атомы будут излучать в моменты различных фаз прецессионного вращения, и в результате степень поляризации понизится. При возрастании поля, а следовательно уменьшении периода прецессии вращение и деполяризация должны возрастать.

Магнитное двойное лучепреломление. Вращательный эффект, обнаруженный Фарадеем, относится к случаю наблюдения вдоль магнитн. силовых линий; в этом направлении компоненты зеемановского расщепления поляризованы по кругу. В поперечном зеемановском эффекте компоненты поляризованы линейно параллельно и перпендикулярно полю(фигура 1). Магнитное поле не влияет на компонент колебаний электрона, параллельный силовым линиям, но влияет на поперечный компонент. Вследствие этого, аналогично циркулярному двойному лучепреломлению в продольном эффекте (эквивалентному факту вращения плоскости поляризации), в поперечном эффекте, вообще говоря, должно наблюдаться обычное двойное лучепреломление, эквивалентное тому, что выходящий свет будет эллиптически поляризованным. Это следствие теории эффекта Зеемана указано Фох-том, причем для величины ожидаемого двойного лучепреломления (для случая области, близкой к линии поглощения атомного газа) ожидаемый эффект, то есть разность показателей преломления обыкновенного и необыкновенного луча, выразится так:

Около самой полосы поглощения двойное лучепреломление по формуле (18) должно обнаруживать аномальный ход и приобретает большую величину. Это следствие теории вполне подтвердилось опытами Фохта и Коттона при поперечном наблюдении натронного пламени в магнитном поле и в позднейших опытах с другими парами и газами. Вдали от полосы поглощения величина эффекта, как это и следует из теории, чрезвычайно мала и практически не м. б. наблюдена. Наряду с указанным магнит-

ным двойным лучепреломлением, являющимся неизбежным следствием эффекта Зеемана, существует магнитное двойное лучепреломление совершенно другого типа (эффект Коттона и Мутона), весьма близкое по своим особенностям к электрооптич. эффекту Керра (смотрите Керра эффект). При поперечном наблюдении ряд органич. жидкостей, обнаруживающих большой эффект Керра, вместе с тем становится слегка дво-якопреломляющим и в магнитном поле. Эффект очень мал и обнаруживается только весьма чувствительными методами. Возникающая разность показателей преломления (для слоя толщиною в 1 см)

μ_π - /fa=C_mlW (19)

(С_т—постоянная, характерная для данного вещества), то есть подчиняется тому же закону, как и эффект Керра. Для нитробензо-лаС_т при 20° равно +2,4· 10¹², для моно-бромнафталина +2,3-10^-12, для сероуглерода—0,42-10^-12. Как и эффект Керра, эффект Коттона и Мутона сильно зависит от температуры.

Для объяснения эффекта Коттона и Мутона м. б. полностью использована современная теория эффекта Керра. Как уже упомянуто, в отношении парамагнитного вращения помимо прецессионного движения атома магнитное поле может проявлять еще ориентирующее действие. Под влиянием поля может происходить намагничивание анизотропных молекул, различное в различных направлениях. Вследствие этого анизотропные молекулы будут стремиться стать по направлению поля. Такому стремлению противодействует тепловое движение молекул: чем <° ниже, тем ориентировка будет более выраженной. Помимо наводимого момента в молекулах могут существовать готовые магнитные моменты, не зависящие от поля, также способствующие-ориентировке. До известной степени моделью такой теории ориентировки может служить большое магнитное двойное лучепреломление в коллоидальных растворах солей железа, открытое Майораной (эффект Майораны). В этом случае магнитное поле действует не на молекулы, а на сравнительно большие частицы из ферромагнитного вещества.

Магнетооптический эффект Керра. Влияние магнитного поля на преломление света в среде должно принципиально сказаться и на отражении света, поскольку теоретически преломление и отражение неразделимы. Такой магнетооптич. эффект отражения найден Керром в 1877 г. при отражении света от металлическ. ферромагнитных зеркал в магнитном поле. При наложении поля меняются фазы и амплитуды компонентов падающего света. Для наблюдения эффекта при нормальном падении применяется следующая установка (фигура 5). Поляризованный николем Ν_τ луч света отражается от стеклянной пластинки р, проходит через пробуравленный полюс магнита, отражается от ферромагнитного зеркала S и проходит обратно через пластинку р и николь Ν₂ к наблюдателю. Наблюдение эффекта именно на ферромагнитных мет связано с огромной величиной постоянной Верде у последних (см. табл, на ст. 393—4). При сильном намагничивании зеркала при отражении происходит вращение плоскости поляризации против вращения тока, возбуждающего электромагнит, и одновременно свет становится слегка эллиптически поляризованным. Опыт пока-.

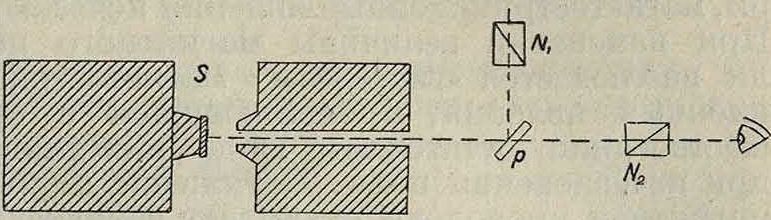
Фигура 5.

зывает, что величина эффекта вращения а пропорциональна намагничиванию I, а не полю Н:

α= Ы. (20)

При косом падении лучей эффект становится значительно больше и сложнее. Теория, в значительной мере только формальная, дана Друде, Гольдгаммером и в наиболее полной форме Фохтом. Для исчерпывающей теории явления нехватает полной теории ферромагнетиков.

Лит.: Хвольсон О. Д., Курс физики, т. 5, Б., 1923; Введенский Б. А. и Ландсберг Г. С., Современное учение о магнетизме, М.—Л., 1929; М и Не г-Р о и i 1 1 e t, Lehrbuch der Physik, 11 Auli., В. 2, Η. 2, T. 2, Brschw., 1929; V olglW., Magneto- u. Elektrooptik, Lpz., 1908; Handbuch d. Elektrizitat u. Magnetismus, hrsg. v. L. Graetz, B. 1, Lpz., 1918; Handbuch d. Radiologie, B. 6, Lpz., 1925; BackE.u. Lands A., Zeemaneifekt u. Multiplett-struktur d. Spektrallinien, B., 1930; Zeeman P., Researches in Magneto-Optics, L., 1913; Wood R., Physical Optics, New York, 1921; Frenkel J., Zur Theorie des Faradayeffektes, «Ztschr. f. Phys.», B., 1926, 36, p. 215. С. Вавилов.