Масса

Масса, постоянное для данного тела отношение между силою, действующей на тело, и вызываемым ей ускорением, характеризующее степень динамич. инертности тела. Пусть на нек-рую материальную точку действует cmi&F и пусть сопутствующее действию силы ускорение точки будет а. Экспериментальным путем доказано: 1) что величина силы F прямо пропорциональна величине ускорения а, 2) что направление силы F совпадает с направлением а. Обозначая постоянный фактор пропорциональности между F и а через т, имеем:

^F=m, (1)

F=та. (2)

Величина т и есть М. данной материальной точки. Из самого определения видно, что т есть величина скалярная и существенно положительная. В частности, если действующая на материальную точку сила есть сила веса Р, а сопутствующее этому воздействию ускорение—д, то аналогично (1) и (2) имеем:

Р —=т, о.	(10
jP=шд	(20
Из (2) и (Г) имеем также:
F=— а. 9	(3)

Пусть, далее, одна и та же сила F действует последовательно на две различные материальные точки, принимающие под воздействием этой силы ускорения «ги <*₂. Т.к.из (1) имеем при этом где т_г и т₂—М. соответствующих точек, то т₁: т₂=а₂: а_и (4)

то есть чем больше М. точки, тем меньше ее ускорение. Таким образом М. материальной точки есть постоянная для данной точки величина, характеризующая степень ее динамической инертности при воздействии сил на нее, вследствие чего М., определенную вышеприведенным образом, называют также коэфициентом инерции или инертной М., в отличие от тяжелой М., рассматриваемой при наличии напряжения поля тяготения (см.-Относительности теория). М. тела обладает аддитивным и свойствами: М. тела равняется сумме М. его частей независимо от способа разделения тела на части. В частности, М. тела равняется сумме М. всех его материальных точек.

Если материальные точки, заполняющие объём V, имеют общую М. т, то средней удельною М. объёма, или средней объёмною плотностью, р_ер. называется масса, приходящаяся на ед. объёма:

Объемной плотностью μ тела в данной его точке А называется предел отношения М. бесконечно малой части тела, окружающей точку, к объёму этой же части при бесконечном приближении последнего к рассматриваемой точке, то есть

/Д т dm.

^д^Ы^У (в)

В общем случае μ — нек-рая ф-ия положения точки А в самом теле, то есть μ=μ(χ, у, г), где х, у, г—координаты точки А по отношению к системе осей координат, связанных с самим телом. Если, в частности, плотность во всех точках тела одна и та же, то тело называется однородным; в противном случае тело неоднородно. В первом случае средняя плотность для любой части тела равняется плотности в любой точке его. Йз (6) имеем для общего случая:

m= Iμ(χ, у, г)· dV. (7)

(V)

Для однородного же тела, т. к. μ=Const, из (7) имеем:

m=yV. (7)

Если материальные точки заполняют определенную поверхность или линию, то аналогичным образом определяются средние поверхностная или линейная плотности, а также поверхностная или линейная плотности в данной точке. Пусть имеется система точек А > А%, .·., А_п, массы которых-равны т₁, т₂, ., ш_п и положения которых по отношению к некоторой системе отсчета с началом О определяются радиусами -векторами г_ъг₂, .,г_п (смотрите фигура). Центром массы или центром инерции данной системы точек называется точка С, положение которой определяется радиусом-вектором г_с, так что

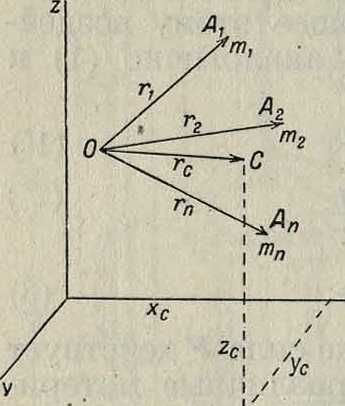
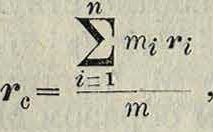
(8)

где m=2 ^тс В декартовых координатах

_ΣηηΗ. _ bЩМ /о

Ус ~ ™ ’ ⁴с т имеем вместо (8)

ZnijXf

О роли центра М. в динамике см. Механика теоретическая. Центр М. совпадает с ц. т. системы. Если материальные точки заполняют нек-рый объём V, то вместо (8) имеем:

I* dm г

(V)

(9)

где dm—М. какой-либо точки или элемента объёма, а г—радиус-вектор, определяющий положение этого элемента. О размерности и единицах измерения М. см. Абсолютная система мер.

Лит.: Felg6ntraeger W., Massenmessung, Handb. d. Physik, hrsg. v. II. Geiger u. K. Scheel, B. 2, Berlin, 1926; Weinstein B., Handb. d. physi-kalischen Massbestimmungen, B. 2, Berlin, 1888; cm. также Механика теоретическая и Относительности теория. М. Серебренников.