> Техника, страница 60 > Мачта антенная

Мачта антенная

Мачта антенная, сетевая опора, сооружение, воздвигаемое для натягивания и поддерживания проводов антенн (смотрите), применяемых в радиотехнической практике. Существуют два главные типа М. а.: свободностоящие и на оттяжках. Свободно-стоящие М. а. (башни) обычно делают из железа как материала долговечного, но их можно строить также и из дерева. Железные антенные мачты очень тяжелы, дороги, но зато они не требуют за собой никакого ухода (кроме окраски) и занимают сравнительно немного места. М. а. на оттяжках строятся как из железа, так и из дерева. Они сооружаются быстрее и легче, и первоначальная стоимость их меньше; к недостаткам их относится то, что они требуют: 1) больше места, 2) более крупных фундаментов, 3) постоянного надзора (лишний штат такелажников), 4) в нек-рых странах (Америка) периодич. смены всех тросов через 5—7 лет. Последнее обстоятельство уничтожает все преимущества первоначальной низкой стоимости, так как после первой смены тросов стоимость этих М. а. становится приблизительно равной стоимости М. а. башенного типа. М. а. на оттяжках бывают жесткого типа, когда отношение длины L всей мачты к радиусу инерции г_г всего сечения L г_г=120 А-150* а I :г_{=10 -f-12, где I—длина участка между ближайшими точками прикрепления тросов. Гибкий тип этих мачт будет при I: г_га;80-Р200. М. а. жесткие

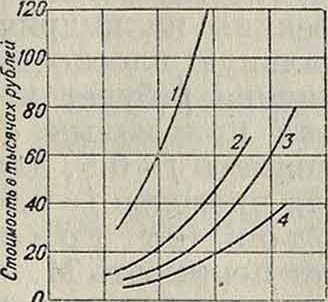
О 50 too ISO 200 250

Высота в uerrwa*

Фигура 1.

По Балырору И Старая φ ηαρ·0,122νί			7	7
/И Но	ая cp-ficp-O.W3
		/А
		/
L*		I

Скорбеть ветра V м/ск

Фигура 2.

выполняются обычно в виде решетчатой фермы. Приблизительную стоимость М. а. можно определить по графику фигура 1. Из него видно, что иапр. при высоте 100 метров железные мачты на оттяжках 3 в полтора раза, трех-опорные 2— в два, шуховские 1 —в шесть раз дороже деревянных 4. Стоимость деревянных мачт при каждом увеличении их высоты на25 метров (начиная от 40 м) увеличивается примерно в 1,4—1,5 раза.

Нагрузка от ветра. Помимо полезной нагрузки (натяжения антенны) мачта должна выдерживать давление ветра. Давление ветра в килограммах/л³ дано в графической форме на фигуре 2. Кривая III, удовлетворяющая ур-ию р=0,1 V-, может быть признана наиболее верной. Для центральной полосы СССР скорости наиболее сильных ветров заключаются в пределах 30—40 м/ск, под тропиками они доходят до 60 м/ск. Пользуясь этими скоростями, легко определить верхний предел давления ветра на М. а. Однако практич. нормы, принятые в раз-

личных государствах, довольно резко разнятся между собою. Это различие наблюдается не только в области максимального давления, но и во взглядах на то, как меняется скорость ветра с высотою. Метеорологией с несомненностью установлено, что скорость ветра с высотою увеличивается. Однако это касается только слабых, а тайнее средних ветров. При сильных ветрах уже на сравнительно небольшой высоте скорость ветра такая же, как и на весьма значительных высотах, вследствие чего давление ветра должно быть принято равномерным снизу и доверху. Расчетная норма, принятая теперь в СССР, р=250 килограмм/м²·. Такая же норма принята и для расчета под тропиками. Для наших широт она конечно велика и безопасно могла бы быть принята в 200 килограмм/м² или даже еще ниже, в особенности для мачт высотою в 100 метров и ниже, для которых уверенно можно допустить р=150 килограмм/м². Для мачт не выше 40 м, если они применяются на радиостанциях не первостепенной важности, можно было бы принять р=75 килограмм 1м², что соответствует буре, граничащей со штормом. Давление ветра на неплоские и несплошные поверхности учитывается введением особого коэфициента обтекания. На него надо помножить величину давления, приходящегося на проекцию внешнего контура поверхности М. а. на плоскость, нормальную направлению ветра. Наир, на круглый цилиндр высотою h, диаметром d давлением ветра Р определяется ф-лой:

Р=· р · d · h,

где /—коэф. обтекания, р—выбранная норма давления в килограммах/м² поверхности, нормальной к ветру, a dh—проекция цилиндрич. поверхности на эту нормальную плоскость. В зависимости от d величина f будет меняться, заметно возрастая при малых d. Для d > 0,5 метров можно принимать — 0,5, для d < 0,5 метров берут=0,66; для проводов /= 0,9.

Нагрузка проводов от гололеда. Обледенение может покрывать М. а. тем больше, чем выше над землей находится то место, где происходит осадка этого обледенения. Поэтому верхушка мачты нагружается гололедом сильнее. Кроме того для различных географических мест размеры гололеда различны. Точно разработанных норм не имеется. Принимают, что мачта равномерно покрывается со всех сторон коркою льда, толщиною 2 см, полагая уд. вес гололеда равным 0,9 и давление ветра > 36 килограмм/м². Для проводов с диам. d принимается следующая норма: при d <4 миллиметров толщина корки льда берется 2 см, при d < 4 миллиметров внешний диаметр гололеда Л=4d.

Натяжение проводов и тросов. Нагрузка тела мачты от веса антенны, равно как и нагрузка его оттяжками (в случае мачт на оттяжках) должен быть определена отдельно из условия крепости проводов и тросов. Провода и тросы рассматриваются как гибкие упругие нити. Будучи подвешены за две точки (например на одной высоте над горизонтом), они располагаются по т. н. цепной линии (фигура 3), ур-ие к-рой

(X X»

е^с+е ^Cj^:=cch

Параметр с входящий в ур-ие (1), определяется чисто механич. данными:

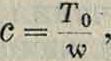
где Т₀— натяжение нити в точке О, a w— вес п. м нити. Чем сильнее натянута нить, тем больше с. Из свойств цепной линии следует, что натяжение в какой-либо точке х T_x=wy,

откуда

Г та х Г₀ К) (у _Гоах У mill) ⁼ (~)

т. о. разница в натяжениях в наинизшей точке и в точке привеса равна весу провода, имеющего длину, равную стреле провеса f. Максимальное натяжение Т_тт можно определить также и по ф-ле:

Т„_шх=Уть + (swf,

где $—длина провода между точками О и В. Угол а определяется по ф-ле:

. $ sw Q с _/оч

tg α= -=_т=г~, или cos α= -, (3)

где 2Q—вес всего провода.

Длина дуги s определяется из ф-лы:

^с)=с sh * (4)

Разлагая в ур-ии (1) eh * в ряд, получим:

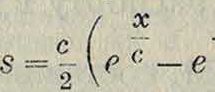
»~[Η·έ©*+*Θ·*·»]·

откуда легко определить провес какой-нибудь точки х:

“,-»—5|ι+!0τ+ί©4.]

Максимальный провес при х — ¹-, где I— пролет,

В электротехнике вообще и в частности в радиотехнике стремятся провода натянуть

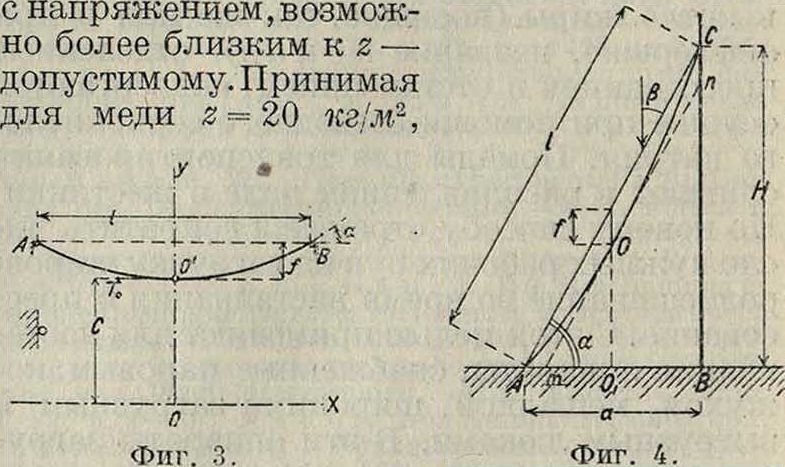
найдем, что например при нагрузке собственным весом w —у F, где F—сечение провода, а у—единичная нагрузка= 0,009 килограмм/м, то есть веси, м провода, приходящийся на 1 миллиметров,² поперечного сечения,

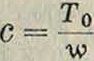
^zi^F У · F

_20

0,009

= 2 222 метров.

В этом случае даже для больших пролетов (I=300 м, I: с=300 : 2 222=0,135):

= 5,06 [1 + 3,8 10-“+5,8 · 10-« + .]. Вёёь ряд в скобках в ур-ии (5) можно принять за единицу и считать, что стрела про-

СО

веса f определяется всегда только первым множителем

Легко заметить, что отношение I: с равноценно отношению f :1. Следовательно замена ряда единицей возможна всегда, когда : I величина малая. Замена ур-ия (5) ур-ием (6) по существу обозначает, что вес провода считается пропорциональным не длине дуги, по которой он располагается, а ее проекции на ось X, или иначе, что вес провода пропорционален длине пролета, над которым он натянут. Это допущение приводит к тому, что цепная линия заменяется параболой. Из ур-ия (6) следует, что

£

I

V>

8То

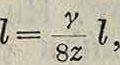
то есть допустимая стрела провеса, при которой провод не перегружается, выраженная в долях пролета, не есть константа, как это часто на практике принимают, но увеличивается пропорционально пролету. Таким же приемом, разлагая ур-ие (4) и умножив его на 2, получим 8—полную длину провода из формулы:

^S=l + 2icz [¹⁺ «о (с) + -]·

Принимая ряд в скобках за единицу, получим:

S=i[l

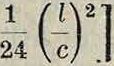
— Ϊ + «

Второй член дает величину, указывающую, насколько провод длиннее своего пролета. Он вообще мал при всех рассматриваемых случаях, благодаря чему S=l, и следовательно провод будет нагружаться не только от поперечной нагрузки wl, но и от колебаний 4°.

Если провод при темп-ре ij подвешен к двум точкам, расстояние между к-рыми I, с некоторой стрелой провеса, соответствующей его поперечной нагрузке и напряжению z_ltкаким провод в этот момент обладает, то можно вычислить новое напряжение провода г, когда изменяются одновременно 4, I и поперечная нагрузка. Перечислим обозначения: w—поперечная погонная нагрузка, которая слагается из собственного веса, веса гололеда и давления ветра; Q=wl— полное поперечное усилие, действующее на о весь провод; q=^ —полная поперечная на т грузка единичного провода; z=р—напряжение провода; Е—модуль упругости провода (но не материала его); а—коэфициент линейного расширения(длямедиа=1,68 · 10~⁵). Пользуясь этими обозначениями, можно показать, что самое полное соотношение для определения напряжения при изменении условий будет:

q²2e

г₂ —

24z²

242?

здесь t₂ и 4_Х—температуры в °С, ΔΪ—удлинение пролета, вызванное например отклонением точки провеса (отклонение вершины мачты). Из этого соотношения, зная начальные г_г, гд, 4_t и £, можно определить новое г₂ при новых t₂, q₂. и 1₂. Определив z_t, одхо-дим по ур-ию (6) новую стрелу провеса.

Для определения, когда провод сильнее будет нагружен—при изменении 4° или при изменении поперечной нагрузки, вводят понятие критического пролета. Если .взятый пролет меньше критического, расчет надо вести по изменению 4°, если же больше—по изменению q. Величина 1_кр — критического пролета определяется следующим соотношением:

кр. ~ Zfmn. i/" 24 Δ4 --_г —j- i (9)

г max min

где Δ4 — разность между 4° при гололеде (равной —5°) при у_тах и 4° наибольшего холода (—30°).

Если провод несет посредине сосредоточенную нагрузку Р, то горизонтальная со-. ставляющая натяжения провода определится из формулы:

гп _ wi² Р1

^1о~ 8 ⁺ Ϊ7

Наибольшее натяжение провода будет у точки привеса и определится из ф-лы:

т_тах=/т² + [^яу

В соответствии с нормами нагрузка провода определяется ф-лами (d, F и D приведены в миллиметров): при d< 4 миллиметров

γ,.=—---р------ кг/м миллиметров²;

при d < 4 миллиметров

γ= 0,136 килограмм/м миллиметров^г.

Давление ветра (без гололеда на проводах): У“. =0,18 Jr;

давление ветра при гололеде;

Уел.=0,0235 §· ·

Результирующая нагрузка при ветре без гололеда:

У рее. - УУсб. + у!. ;

при гололеде же:

Урез. ~ У (Усб. 4“ У г.)² “Ь У гл,. · Поперечную нагрузку получим, умножив γ на длину пролета 4, так как q=γί.

Схема расчета антенных проводов сводится к следующему. Предварительно выясняют величину критич. пролета по ур-ию (9) для заданных z_d, γ _б γ_υ при гололеде и ветре и ij=—5° и ί₂ ’= —30°. Его величина укажет, чтб для провода будет опасным— охлаждение или поперечная нагрузка. Узнав опасные условия, по назначенному уже допустимому напряжению ζ (запас прочности обыкновенно выше 3 не берут) и по ур-ию (8) вычисляют то напряжение ζ₀, с которым провод должен быть подвешен. По ζ₀ вычисляем’ стрелу провеса f₀ (с которой ставится в момент подвешивания провод), пользуясь ур-ием (6). придав ему вид:

/0=^· (10)

При обычных в практике длинах антенны для обычно применяемых антенных канатиков расчетной нагрузкой является почти всегда гололед или ветер, а не температурное сокращение проводов.

Мачта на оттяжках. Оттяжка (фигура 4) являетсй тросом, подвешенным не горизонтально, как то было для антенны, а наклонно. Пролетом здесь будет АВ=а, то есть проекция троса на плоскость, перпендикулярную к действующим на него силам. Основное уравнение напряжения такого троса:

q$COS²a₂E Q^COS²ctj E, ME

^Ζ2 24ζ| ~^Ζΐ 24 ζ I

Угол а есть дополнение к углу β между оттяжкой и действующей на нее силой; остальные обозначения те же, что и для горизонтального провода. Так как q cos а—слагающая, действующая поперек провода, то смысл этого ур-ия тождествен с ур-ием для горизонтального провода. Эта поперечная нагрузка определяется как произведение величины а на величину погонной результирующей нагрузки на трос. Трос располагается по параболе. Наибольший провес у него будет посредине пролета—в точке О. Для этой точки имеем следующие выражения, определяющие: Т_гор—горизонтальную составляющую, P_eepm.—вертикальную составляющую и Т_полн,—полное натяжение:

т=п -Q- р — т т Q · т — 7 -Q.

-* гор. $f ^{9 метров ee}P^m· ~ 8 ’ пот. ⁰ %f

Касательная в точке О параллельна линии АС, соединяющей точки привеса. Заметим, что такими же ф-лами будут определяться натяжение и его составляющие Т-образной антенны в середине ее полупролета. Величиною Р_верт. будет тогда половина веса снижающихся проводов Р_с. и ®/₄ веса горизонтальной части Q, расположенной над всем пролетом I между точками привеса. Стрела провеса антенны определится ф-лой:

j_ Ql i Pp.l

¹ ~ 8To 4Tо

Если вдоль мачты действует усилие Р_ж, то для сохранения ей прямолинейной формы необходимо, чтобы тросы были натянуты с напряжением г, к-рое удовлетворяет следующему условию:

12

у²а²Е EFh cos² а

I^е

V 2 Р_м.а

-г где h обозначает расстояние вдоль по мачте между точками прикрепления оттяжек (между узлами). Основное ур-ие для троса показывает, что при больших напряжениях провес перестает играть заметную роль и сложная (кубическая) зависимость напряжения троса от перемещения Δ точки привеса приближается к зависимости линейной. Наличие прямолинейной части графика позволяет сделать заключение, что здесь трос работает как стержень, у которого сечение равно сечению троса с весьма плавно меняющимся модулем упругости Е_ф., величина которого определяется из ур-ия:

тт _ _^_ гр

^ΛФ (<2COSa)2E

^{1 +} 12Z®

где q cos a—величина поперечной нагрузки, Е—модуль упругости троса (без поперечной нагрузки) и z—напряжение, при к-ром определяется Е_ф, Из этого ур-ия следует, что выгоднее брать возможно тонкий трос и ставить его с возможно большим напряжением, так как при этом скорее достигается работа на прямолинейной части и Е_ф. будет больше (мачта не будет качаться из-за наличия «слабины» в тросах). Можно пока-

(Q COS α)²Ε

зать, что член — 3—увеличивается при-

близительно пропорционально d“, где d— диаметр троса.

Поперечная нагрузка для наклонно повешенных тросов при изменении ветра меняется весьма значительно. На фигуре 5 показан способ нахождения новой поперечной нагрузки. Первоначальная погонная нагрузка q_c6_, поперечная от нее ар, q_e,—погонная нагрузка от ветра; очевидно, что q_e=— р sin а, где р—принятая норма погонного давления на провод, подвешенный нормально к ветру. На наш провод действует лишь нормальная слагающая ас. Полная результирующая нагрузка q_pe3_ и поперечная ср=са+ар. Пролет, под которым теперь располагается провод, уже не а, но а_х; при этом а_х берется под прямым углом к q_pe3_ Очевидно, что ср 1=q_pe3. а_х. Одну из оттяжек ветер будет нагружать, другую разгружать. На фигуре 6, как и раньше, аВ—мачта, а А и аА_г— оттяжки; ab=q_c6., ас—нормальное к оттяжке давление ветрα= р₀ sin² a. Результирующая нагрузка q_pe3_=ad. При обратном движении

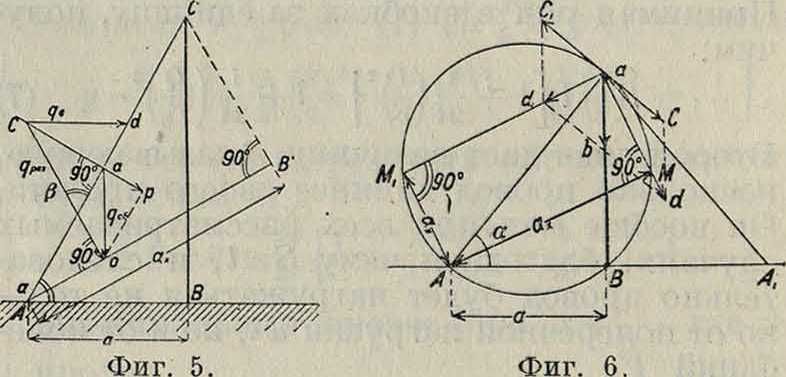
ветра q_pe3.=ad_u Описав окружность на оттяжке, как на диаметре, найдем новый пролет для нагруженной оттяжки AM, а для разгруженной АМ_г. Поперечная нагрузка будет для первого троса AM - ad, а для второго АМ_г ad_u Так определяется поперечная нагрузка для тросов продольных, то есть лежащих в плоскости ветра. Определение поперечной нагрузки для тросов поперечных, то есть лежащих в плоскости перпендикулярной к направлению ветра, дано на фигуре 7 методом начертательной геометрии, как наиболее быстро приводящим к цели. Здесь ху линия пересечения плоскостей проекций, О А—вертикальная и АА_г—горизонтальная проекции поперечной оттяжки. Движение ветра—вдоль по оси XY. Оа—вертикальная проекция погонного собственного веса (проектируется без сокращений); горизонтальная его проекция—точка А. Проекции погонного давления ветра р_в_ даны отрезками ОЬ и А. Так как провод перпендикулярен направлению ветра, то р_е. равно принятой норме давления ветра на провода. Проекции результирующей—Ос и АЬ_г. Чтобы найти новый пролет, из нижней точки крепления оттяжки, из точки A At опускаем перпендикуляры на результирующую Ос— Ab₃. Проекции его будут АВ и A_tB₁. Проведя окружность из центра О, радиусом ОО_х, равным истинной длине оттяжки, найдем истинную длину А₃В_х перпендикуляра АВ,

к-ргя выразится отрезком СВ; он и выражает величину нового расчетного пролета. Поперечная нагрузка будет определяться как СВ- Ос. Аналогичными методами определяется поперечная нагрузка для случая, когда ветер дует по направлению между оттяжками. Для примера на фигуре 8 даны полярные диаграммы поперечной нагрузки для оттяжек из железного телеграфного провода

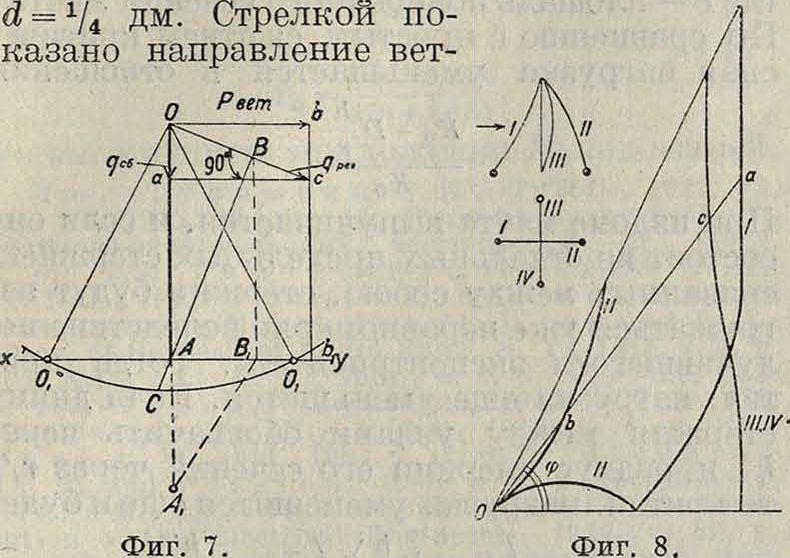
ра. Если тройы подвешены под углом φ к горизонту, поперечная нагрузка первого троса выразится отрезком Оа, второго—Оb и третьего—Ос. Соответственно этому натяжение тросов будет велико у I, III и ΙΥ и слабо у II. Напряжение каждого из этих тросов определяется по основному ур-ию. Фигура 9 дает ход изменения напряжения любого из этих тросов с изменением поперечной нагрузки, если тросы подвешивать с различным первоначальным напряжением 2_Хпри начальной поперечной нагрузке 0,16.

Выбор тросов для М. а. ведется по ур-иям, связывающим прогиб мачты с натяжением оттяжек и с горизонтальным усилием в рассматриваемом узле мачты, где крепятся эти тросы. Горизонтальные усилия Q создаются давлением ветра как на самую мачту—Q_M_, так и на тросы Q_mp.; Q.u.—давление, действующее на мачту вблизи узла О, на длине, равной половине расстояния до смежного узла (в каждую сторону от узла О); Q_mp.—половина всего давления на тросы, прикрепленные к узлу О. В самом верхнем узле, где крепится антенна, действует еще горизонтальное усилие от нее. Слагая (геометрически) все эти усилия, найдем их сумму, которую разложим на две составляющие: по мачте—<2ι и нормально к ней—Q₀. Усилие Q₀ воспринимается соответствующей парой тросов. Запас прочности тросов берется ~3 (для неответственных М. а. можно брать 2,5 и даже 2). Первоначально сечение троса определяют приближенно, задавшись размерами мачты и определив примерно величину Q₀. Тогда сечение троса определится из ф-лы:

F =

___0»__

^^доп· 3) COS ci

Проверив и исправив величину Q₀, переходят к более точному расчету. Легко видеть (фигура 10), что

Т_г COS а — Т₂ COS α= (Jo,

или

At=Т₁

_ Гр ___ Qo ² COSH

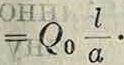
лн;

Величина Q₀ ~ известна всегда, когда известны размеры мачты и троса (известно Q₀). Отклонение мачты Δα связано с удлинением расстояния АС между точками привеса троса следующим образом:

Величиною Аа задаются. От правильного выбора ее зависит по существу то давление, которое будет испытывать мачта от тросов: чем Аа больше, тем давление меньше. Величину Аа обыкновенно берут 1—2% от высоты h; ее следует в расчетах уменьшать для тех узлов, которые лежат ниже, так чтобы ось мачты была прямой линией. Правильнее было бы однако ось мачты располагать по окружности, т. к. мачта обычно защемлена у основания, переносить же весь прогиб книзу—значит увеличивать напряжение в наиболее опасном месте. Брать Аа большим не следует, так как мачта получается «жидкой» и, несмотря на свою гибкость, все же может получить чрезмерные напряжения, тем более, что давление ветра вдоль мачты, хотя и сохраняет в среднем свою величину, но в каждый момент времени м. б. различно в различных точках. Поэтому лучше брать Аа ближе к 0,01-1-0,0125 h. Необходимые для расчета величины связаны следующими соотношениями:

II 1 «s4	T i - T 2 F	Qol. : a ’	(11)
q E	ql E	ME	(12)
,=Zn -	--Ч +
242 j	azl	l
qlE 242-2 °	qIe 242q	ME T ’	(13)

Здесь ζ₀ и q₀—напряжение и поперечная нагрузка тросов до появления ветра и возникновения усилия q₀ z_x и q_t—те же величины при ветре для нагруженного троса, а «з и 5, для разгруженного ."В этих ур-иях, (11), (12) и (13) имеются величины 2₀, г₁₍ 2,

Z
				z1
			k	У
		k
	0.16

О 0.1 0.2 03 0.4 0.5

Поперечная нагрузка

Фигура 9.

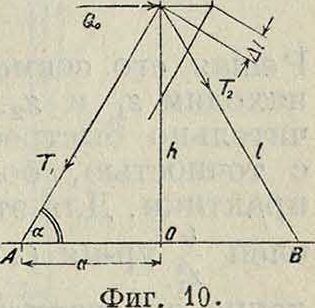
Az и А1. Задаваясь двумя из них, определяют три остальных. Наилучшим решением было бы то, которое дает наибольшее z_u равное допустимому г_доп_. При тяжелых тросах это однако обходитсядовольно дорого, т. к. мачта получается наиболее жесткая, а потому и тяжелая. Поэтому тросы с большим запасом прочности ставить не следует.

Рассмотрим три наиболее существенных случая. 1) Наиболее жесткая мачта. Это будет при наибольшем напряжении наветренного троса, так как прогиб мачты будет наименьшим. Поэтому допускаем для работы этого троса максимальное z_mm, сле-довательно Zt^z._dM/, Az= — =. Ищем z₂.

qlE	Ζχ + ζ2	_ i [«!»,«!£ 2 24 zj 24 zf
24z0	2
II Ез < 1 —	Z1 — Ζ2	1 (4ΪΕ «1Ε
	2	2 24 ζ 24 ζ

z₀ и M. Определяем натяжение ζ₂ подветренного троса:

ζ₂=ζ₁ — Δζ.

Складывая и вычитая ур-ия (12) и (13), получим:·

₊ (М)

(15)

Правые части этих уравнений известны, так как и уже определены. Поэтому легко определяются начальное напряжение z₀ и ΔΙ, а по ней отклонение мачты Да. Так как все тросы (поперечные и продольные) ставят с одинаковым начальным напряжением z₀ (иначе мачта не будет прямолинейна), то легко найти напряжение z₃ поперечных тросов при ветре. Для этого пользуемся уравнением (8), полагая в нем ΔΪ=fj — f₂=0 и беря ζ₀ из ур-ия (14):

(16)

__ QjE _ <Ц]Е

³ *4*1 ~ 244

Зная напряжение всех тросов, определяем слагающую вдоль по мачте. 2) Проверка троса на предельную нагруз-к у Q₀. Дано (выбираем): г_г=z_dm/, Δα равно максимальной допустимой величине. Вычисляем: по Δα величину Δ1= Δα. Зная

ΔΙ и z_lt по ур-ию (15) определяем z₂. Зная г_х и г₂, определяем предельное горизонтальное усилие, Q₀, которое м. б. воспринято тросами при прогибе мачты, не превосходящем допустимой величины:

Q.⁽; ΔΓ—г Ρ&ι-*ύ·

ζ₀ находим по ур-ию (14) и г₃ по ур-ию (16).

3) Точный выбор рабочих напряжений тросов. Дано Δα и Δζ=$¹ ;

г CL

Z i — Ζο

Δ Ζ

ΊΓ

(17)

Тогда определяем ζ_λ=Δ ζ + ζ₂ и

Подставляя эти значения в уравнение (15), получаем:

а Ь ^ζ *i

Решая его совместно с ур-ием ζ₂ — ζ₁= Δζ, находим и г₂. Задача эта решается значительно быстрее приближенным способом с точностью, более чем достаточной для практики. Для этого обратим внимание, что член _а ур-ия (17) изменяется весьма мед-^ζι

ленпо по сравнению с другим членом. Задавая ему наиболее вероятное значение, превращаем ур-ие (17) в квадратное, к-рое легко решается.

Расчет тела мачт. Выяснив нагрузки на тело мачты, можно подобрать нужные его размеры, пользуясь ф-лами строительной механики. Отметим здесь лишь следующее. С достаточной для практики точностью расчет М. а. можно вести, считая, что в местах прикрепления оттяжек имеется шарнир. Обозначив расстояние между узлами через h, для расчета пользуемся ф-лой Тетмайера, которая дает величину критич. напряжения в виде к_кр,=К₀ -J-·!) ^

и приложима, пока 10 < ^h < (100 4-105).

^гг

Здесь г,· — радиус инерции всего сечения мачты, К₀ — временное сопротивление на сжатие (для железа К₀=3100 килограмм 1см², D=11,4; для дерева Д₀= 293 тег/см² и D= 1,97). Разрушающая нагрузка будет

P_Kp.=F-k_Kp.=F(K₀-D§,

гдеF—площадь поперечного сечения мачты. По сравнению с простым сжатием критическая нагрузка уменьшается в отношении

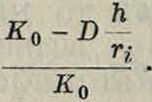
При изломе мачта выпучивается, и если она состоит из отдельных предельных стержней, связанных между собою, стержни будут нагружаться уже неравномерно вследствие получившегося эксцентриситета. Тогда крк-тнч. нагрузка еще уменьшится. Если длину стержня между узлами обозначить через h и радиус инерции его сечений через r_t то критич. нагрузка уменьшится еще и будет

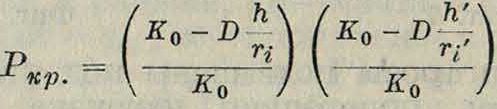
Необходимо считаться с эксцентриситетом, получающимся от неравномерного подведения нагрузок. Т. к. тросы при ветре натянуты неодинаково, то нагрузка мачте передается с эксцентриситетом, к-рый при изломе увеличивается еще больше. Расчет связей (прокладок или решеток) делается на общих основаниях.

Расчет фундаментов и фундаментных кольев. Допускаемое напряжение грунта а_х увеличивается с глубиной по формуле (в т/м-у.

^σχ — Ttg² ^45 + I j=fc ж,

где Г—вес земли в т/м³, 4—угол естествен, откоса, х—высота засыпки до рассматриваемого сечения в м, к—фактор пропорциональности. Величина реакции от грунта (при выворачивании) Р_й_ определяется по ф-ле: ahxl Ф-=— ’

где х₀=~, h—глубина погружения фундамента (или кола), а—ширина фундамента (или кола). Момент, действующий на фундамент (или кол) со стороны грунта, М определится из ф-лы:

М =

akh³ 24

9_

16

ьРф.·

Зная Ж, мол-сно узнать силу Р_х, больше которой нельзя передать фундаменту:

где х₀+У—плечо силы Р_х. Ширина фундамента а связана с выворачивающим моментом соотношением:

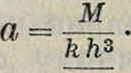
24

Если учитывать расширение сдвигающихся слоев, то новый момент М„ определится из уравнения:

М_д=ψΜ,

где

Ч> =

’2(10 + 12/3h -1-302 h2)

5(4 + 30fl)

β=·

tg

(^{45 +} l)

Следовательно где

p,=

4α y> M

Λ-ο + У 4 /i + 3 β h ²

° 2 (3+2 β h)’

у—высота точки приложения Р_х над землей.

Лит.: Т у р л ы г и н С. Я., «ТиТбП», 1922, 13, стр. 266, 1925, 28, стр. 33; Виноградов Η. И., «Технико-экономический вестник», М.—П., 1922,

3, стр. 273; Тимофее в-Р а д з и в и л л В. И., «ТиТбП», 1922, 15, стр. 489; его же, «Жизнь и техника связи», Москва, 1924, 11; W e a g a n t 11. А., «Ргос. of the Inst., of Radio Eng.», N. Y., 1915, v. 3, p. 135; Elwell C. F., ibid., v. 3, p. 161, 1920, v. 8, p. 193; Davis G. S., ibidem, 1915, v. 3, p. 171; Milieu er Fr. H., ibidem, 1918, v. 6, p. 192; Buel A. W., ibid., 1924, v. 12, p. 29; Mlcehiar-d i B. and P e s s i о n, ibid., v. 8, p. 156; Bour-seire M., «GC», 1923. 4 aoiit; «Journal of the Institution of the Electrical Engineers». 1929, v. 67, p. 229. Приводимая библиография касается лишь мачт на оттяжках или специфических условий работы свободностоящих башен. С. Турлыгин.