> Техника, страница 60 > Маятник

Маятник

Маятник, твердое тело, качающееся около горизонтальной оси под действием силы тяжести. Различают М.: математический (или простой) и физический.

I. М. математический, или простой,—Материальная точка, вынужденная перемещаться без трения по окружности, расположенной в вертикальной плоскости. В частности, это вынужденное движение могло бы быть осуществлено при помощи невесомой нити, один конец которой укреплен в неподвижной точке, а к другому концу подвешена тяжелая материальная точка.

Если О—центр окружности, по. которой перемещается точка, I—радиус окружности (длина нити), О В—вертикаль, проходящая через О, В—начало отсчета дуговых перемещений а точки по окружности, А—гна-

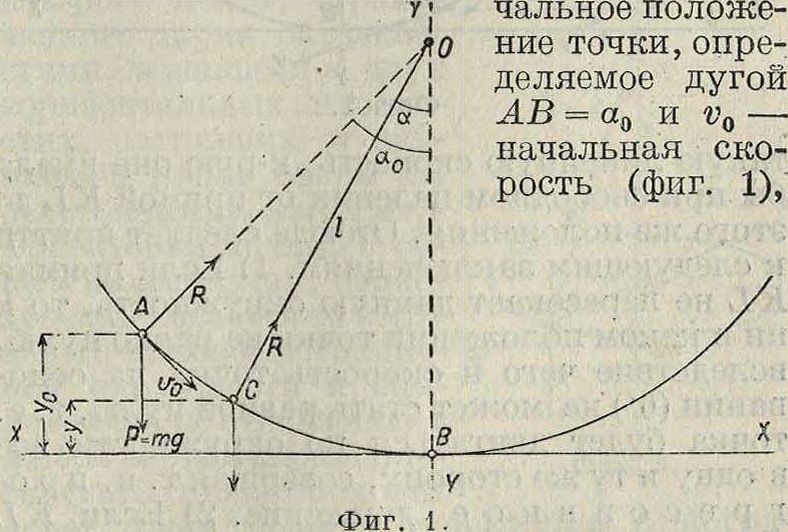
то уравнение движения точки, выражающее функциональную зависимость параметра а от времени 1, будет:

1Й + Г sm«-=0 (1)

[см. Колебательное движение, ф-ла(17)]. Во время движения точки на нее действуют сила веса P=mgr и сила реакцйи связи В, причем, т. к. последняя нормальна к траектории в любой ее точке, то работа силы В равна нулю, так что работу совершает только сила Р. Применяя к рассматриваемому случаю теорему живых сил (смотрите Механика теоретическая), имеем:.

й р™²)=dT=Y dy=—Р dy=— mg dij (2) или

d (v²)=—2(7 dy. (3)

Интегрируя (3), имеем следовательно:

v²=— 2ду + Const. (4)

Если в начальном положении А точки, определяемом у₀, скорость равнялась v₀, то

Const=vl + 2 ду₀, (5)

так что имеем из (4):

v²=- 2ду + vl + 2ду₀=2д (7t₀ +у₀- у), (6) где /г₀—высота, на которую поднялась бы точка, брошенная вертикально вверх со скоростью v₀ из положения А, так как высота у2

К определяется из равенства h₀=⁰. Про-

"9

ведя на расстоянии fe₀ от А прямую KL, параллельную XX (фигура 2), получим, что в положении С точка находится от KL на расстоянии h=h₀ + у₀ — у, так что из формулы (6) имеем:

v²=2gh. (6)

Т. о. при своем движении по окружности точка будет иметь в любом своем положении

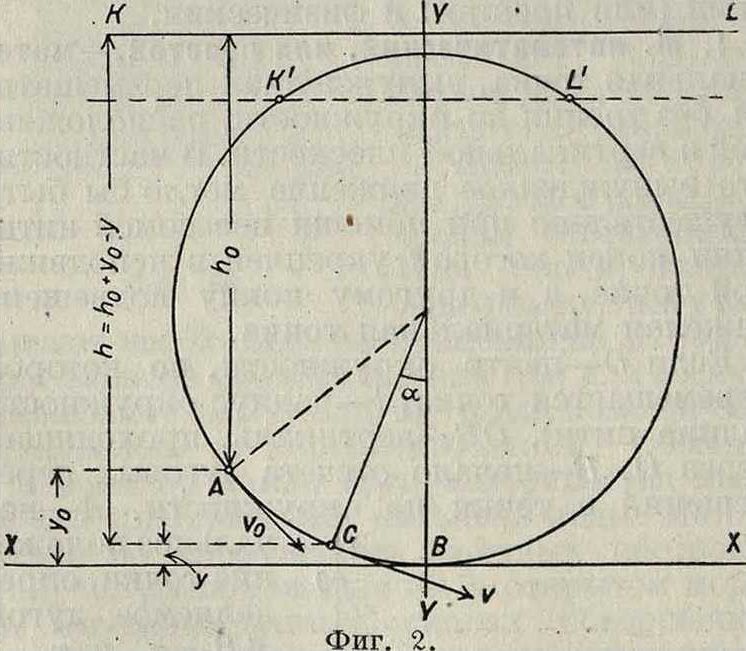
такую линейную скорость, к-рую она имела бы при свободном падении от прямой KL до этого же положения. Отсюда следует прийти к следующим заключениям. 1) Если прямая KL не пересекает данную окружность, то h ни в каком положении точки не равно нулю, вследствие чего и скорость точки на основании (6) не может стать равной нулю, то есть точка будет двигаться по окружности все в одну и ту же сторону, совершая т. н. прогрессивное движение. 2) Если KL пересекает окружность в точках К и L, то, т. к. в этих точках h=0, при достижении движущейся точкой этих положений скорость ее становится равной нулю, меняя в дальнейшем свой знак на обратный. Точка в этом случае следовательно совершает колебательное движение. 3) Если KL касается окружности, то движение будет асимптотическое. Обычно, когда говорят о математическом М. в узком смысле слова, то подразумевают наличие условий, при которых имеет место колебательное т движение. Для определения полупериода „

колебательного движения, то есть промежутка времени, истекшего между Двумя крайними положениями точки, имеем из (1):

(Д ⁼ ~ - cos и₀. (7)

dt=-г/~- — ^da.~,

* 2д ) cos а - cos а₀

откуда, если /₀—промежуток времени от начальн. положения А до положения В, имеем: ίο _ “о

^Т-=2 fdt=i/~~ Р— ^da--- (8)

“ “ V Q О i cosa — COSan

О 0 ’ "

Интеграл в правой части (8) м. б. преобразован еще и следующий образом. Заменим переменное а переменным и, связанным с а соотношением:

sin -|·=и sin “° (9)

Диференцируя последнее равенство, получаем:

cos “ da=sin ~ du=k du, · (10)

. где k=sin ”°. Кроме того имеем: cos а — cos a₀=2 (k² — sin² ) =2(fc²—u²k²), (11)

cos .-,=11— u²k².

(12)

Принимая во внимание равенства (10), (11) и (12), а также и то, что при изменении a от а₀ до 0 переменное и изменяется от 1 до 0, имеем из (8):

1

^du (13)

^=2ιΛ⁷ L

2 V 9 J ] (! _ 0

М2) (l-fe2«2)

Интеграл правой части (13) представляет собой эллиптич. интеграл 1-го рода. Разлагая --¹-. в ряд по биному Ньютона. ] 1

имеем:

со

(1 - к²и²)=2 С_пк^2п

(14)

где п=0 1-3-5.(2п - 1)

Ό - 2-4-6 .2п

Подставляя (14) в (13), получаем:

(п > 0).

СО 271

du

(15)

η=0 0

и так как интеграл правой части (15) равен то следовательно имеем: Т=2луЛУ 2 Clk-

(16)

или в развернутом виде:

Т=2я/{! + (‘)⁵

sin·

2 _i_

+ - + (4^“)^2sin2B ?+··} a-)

При достаточно малых значениях а₀ все члены последнего ряда за исключением первого ничтожно малы, так что в этом случае имеем:

Т=2π у^Г‘ (18)

В последнем случае очевидно период Т М. не зависит от величины начального угла отклонения а₀ (аномалии, амплитуды). Такого рода движение М. называется изохронным. В общем случае, как видно из (17), движение М. не будет изохронным. При а₀ < 22° ошибка при пользовании ф-лою (18) менее 1%. Практически можно пользоваться для определения величины Т следующей ф-лой, дающей ошибку менее 1% при а₀< 70°:

Τ=2πγ^Γ-_д [1+ 0,0019 ("₀°)²J · (19)

Все приведенные выше ф-лы были выведены в предположении отсутствия сопротивляющейся среды. Если же точка движется в среде, оказывающей противодействие, прямо пропорциональное линейной скорости V точки, то, так как угловая скорость

da

со=jj- пропорциональна v, аналогично та-

кому же случаю прямолинейного движения [см^ Колебательное движение, формула (32)] нужно будет к левой части ур-ия (1) прибавить член 2п ~, так что ур-ие движения примет вид:

~ + 2п ~ -]- fc² sin α= 0, (20)

где к=У ? · При достаточно малых колебаниях ур-ие (20) м. б. заменено ур-ием:

aS + 2»ar + ^fc,e-o· (2D

В последнем случае период колебания

Т =.

У&²-П²

(22)

Аналогично случаю прямолинейного движения последовательные амплитуды а₀ будут составлять убывающую геометрич. про-

πη

j/fe2_n2,

грессию со знаменателем, равным е так что колебательное движение М. будет затухающим.

Если находящаяся в вертикальной плоскости кривая, по которой вынуждена пере-

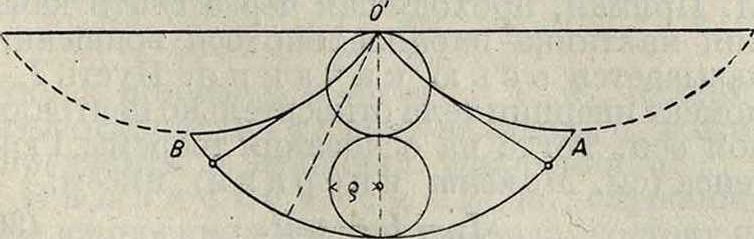
о

Фигура 3.

мещаться точка, представляет собой циклоиду, то М. называется циклоидаль-н ы м. Так как кривая циклоиды представлена yD-ием

s²=8 еу, (23)

где ρ—радиус круга, образующего циклоиду (фигура 3), то имеем:

%=й=^С0*У’ (2⁴)

где у есть угол, образованный вертикалью с касательной, проведенной к циклоиде в сторону возрастающих дуг. Проектируя обе силы В и И на направление касательной,

имеем, по основной формуле динамики и принимая во внимание (24):

d²s

m -

mg cos у=_dti

или

di² 4ρ

откуда имеем для периода колебания:

(25)

(26)

Из последнего равенства видно, что период колебания циклоидального М. не зависит от начальной аномалии а₀, вследствие чего он называется М-.изохр онным или таутохронным.

Известно, что развертка ЛОВ циклоидыИОВ есть также циклоида,

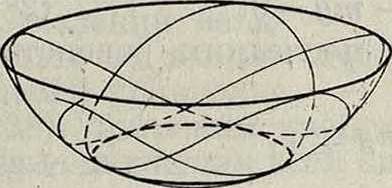
Фигура 4.

Фигура 5.

равная данной. Пользуясь этим, можно осуществить изохронный М. длиною ϊ=4ρ, заставив гибкий стержень ОО при своем качании около точки О огибать поочередно две ветви циклоиды АО и ВО. Точки направляющих ветвей циклоиды являются мгновенными центрами вращения при качании маятника. Попытки практическ. применения циклоидальных М. для часов положительных результатов не дали.

Сферический маятни к—материальная точка, вынужденная перемещаться по шаровой поверхности. Если точка в начальный момент начинает свое движение в горизонтальном направлении, то она движется по шаровой поверхности внутри нек-рого пояса, ограниченного двумя окружностями, лежащими в двух горизонтальных плоско- *

стях, отстоящих от наи-низшей точки сферы на расстояниях^ иг₁(г₂>г₁).

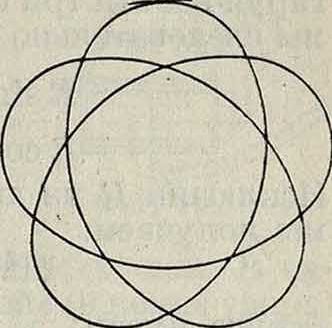
Траектория точки, в общем незамкнутая, периодически касается то верхней то нижней погранич-ной окружности и симметрична по отношению к любой вертикальной плоскости, которая проходит через точки йасания траектории с пограничными окружностями (фигура 4). Нижняя пограничная окружность лежит всегда в нижней полусфере. Проекция траектории на горизонтальную плоскость имеет вид, представленный на фигуре 5. В частности можно придать сферич. маятнику начальную горизонтальную скорость такой величины, что точка будет перемещаться равномерно по окружности, лежащей в горизонтальной плоскости. В этом случае маятник называется коническим.

Пусть будет радиус сферы ОА=I (фигура 6); радиус окружности, по которой точка пере-

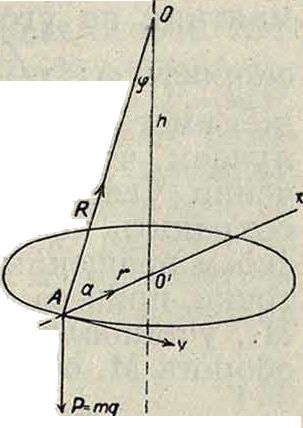
мещается, 0А=г; φ—угол, образованный радиусом сферы О А, проходящим через данное положение А точки, и вертикалью. Т. к. точка движется по окружности равномерно, то полное ускорение а все время направлено по радиусу к центру окружности (смотрите Механика теоретическая)·, вследствие этого сила инерции I точки при ее движении также направлена по радиусу, но в сторону противоположную а. Во время движения точки на нее действуют сила веса Р=тд и сила реакции связи R. Если бы к этим силам прибавить силу инерции 1= — m^v* а_1г то точка находилась бы в равновесии. Проектируя все эти три силы на прямые АО и 00, мы следовательно имеем:

Rsm<p— ™²=0, (27)

R cos φ — mg=0. (28)

Исключив R из двух последних равенств, мы получаем:

mv²,

—=mg tg φ,

откуда имеем:

V=V gr tg ψ=г/£, (29)

где h=00. Угловая скорость, с которой точка перемещается по окружности, будет равна

(30)

г У h У I cos φ ⁴ ·,

Т. о. для того, чтобы точка А равно-мерно перемещалась по горизонтальной окружности сферы, необходимо ей сообщить начальную горизонтальную скорость, равную r |. Из (30) видно, что каждому оп ределенному значению ω соответствует определенная величина угла φ, причем с увеличением ω увеличивается и φ. Для того чтобы φ=90°, следовало бы придать точке угловую скорость ω=οο. Если, отклонив маятник на угол φ, придать ему угловую скорость ω <.

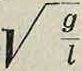
то равенство (30) не мо жет иметь места, так как в этом случае получаем, что cos^>l. Т. о. при таком значении угловой скорости угол ψ не может сохранить постоянной величины и М. при своем вращении будет также качаться около точки привеса по закону движения сферич. М., установленному выше. Период полного оборота М. очевидно равен гг, 2л icos ϊ q Z h /Q1

Τ= _ω=2π| _g=2πγ _g. (31)

Конич. маятники имеют большое технич. применение в т. н. регуляторах (смотрите), применяемых для того, чтобы известная часть машины сохраняла во все время работы некоторую постоянную и необходимую для данных условий работы скорость (центробежные регуляторы Ватта, Портера, Фарко, Гроссмана и прочие).

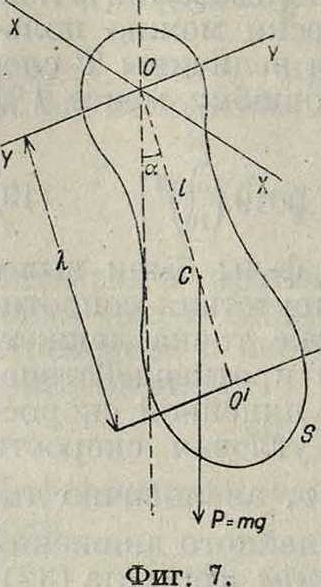
2. Физический маятник—твердое тело, свободно качающееся около горизонтальной оси под действием силы тяжести. Так как осуществить математический М. со всей строгостью невозможно, то в действительности существуют лишь физич. М. Пусть имеем тело S массы т, подвешенное к горизонталь ной оси YY, не проходящей через ц. т. тела (фигура 7). Координатная плоскость XOZ пусть проходит через центр тяжести С тела. Если отвести тело на некоторый угол а_а в сторону от положения равновесия и предоставить его самому себе, то тело начнет колебаться около оси, причем имеет место равенство (смотрите Механика теоретическая):

sI_v-M_y, (32) где ε — угловое ускорение, I — момент инерции тела относительно оси вращения Υ, М_у—сумма моментов относительно оси Υ всех внешних сил, которые действуют на тело. Внешними силами, действующими на тело, являются в данном случае сила веса тела JP== тд и силы реакции оси. Так как момент последней силы относительно оси равен -нулю, а момент первой силы в положении тела, определяемом углом а, равен PI sin а, где I— расстояние от С до оси У, то из (32) имеем: el_y=mgl sina, (33)

откуда получаем:

dm mglsina roor

Найдем далее длину Я такого математич. маятника, к-рый качался бы точно так же, как и данный физич. маятник, то есть к-рый имел бы в положении, определяемом углом а, такое же угловое ускорение, как и тело. Аналогично (33) имеем:

ем Я²=mgl sin a, (34)

где т—масса математического Из (33) и (34) имеем:

маятника.

(35)

Длина Я называется приведенной длиной физич. М. Отложив на прямой ОС от точки О отрезок 00=Я в сторону С, получим т. н. ц е н т р качания физич. М. Прямая, проходящая через центр качания маятника параллельно оси вращения, называется осью качания. Пусть 1_С— момент инерции тела относительно центральной оси. Тогда на основании теоремы Гюйгенса (смотрите Момент инерции) имеем:

1_у=1_с + тР. (36)

Из (35) и (36) имеем далее:

Х ₌ к±г^1₌Ш₊1. (37)

ml ml

Так как ~ > 0, то Я > Z, то есть приведенная длина физич. М. больше, чем расстояние от оси привеса до центра тяжести М. Нетрудно доказать, что если ось качания сделать осью вращения М., то прежняя ось вращения станет осью качания. Это свойство физич. М. послужило для устройства т. н. оборотного М., впервые предложенного Катером (фигура 8) для более точного определения ускорения д силы тяжести.— При помощи соответствующего регулирования достигают того, что периоды качания

М. около двух осей 00 и ОО равны между собой. Расстояние между осями дает тогда приведенную длину Я физич. М. Зная же период качания и приведенную длину Я, определяют у из (18).

Свойствами физич. М. пользуются в технике при практич. определении моментов инерции тел методом качания (смотрите Момент инерции). Качания физич. М., состоящего из тяжелого шара, подвешенного на длинной нити, послужили Фуко для доказательства суточного вращения земли около своей оси. Плоскость качания М., сохраняя неизменным свое положение по отношению к звездному пространству, меняет однако это положение по отношению к земной поверхности. Угол поворота плоскости качания в течение суток равняется Ζπ sin φ, где φ — географич. широта данного места. На полюсе следовательно в течение суток эта плоскость сделает полный оборот, а на экваторе она останется неизменной. Для тех же целей маятник Фуко был усовершенствован впоследствии Кам-мерлинг-Оннесом. Маятником в виде шарика, подвешенного на нити, пользуются также для определения величины ускорения движущегося тела, к которому М. для этой цели и подвешивается (маятник Дедуи). Если подвесить например в вагоне поезда М., то при неравномерном движении поезда М. отклонится в сторону, противоположную направлению ускорения. При этом на шарик действуют сила В, натяжения нити и сила веса его Г. Если приложить силу инерции I=—та, где а—ускорение поезда (фигура 9), то все эти силы, по началу Даламбера (смотрите Механика теоретическая), должны взаимно уравновеситься, вследствие чего равнодействующая сил I и JP должна иметь направление, совпадающее с направлением нити М. Если нить отклонена от вертикали на угол а, то мы следовательно имеем:

откуда получаем a=gtga. Т. о., измерив угол отклонения а и зная величину д, можно определить и величину ускорения а.

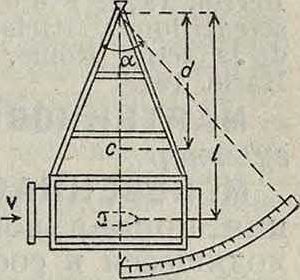
Баллистический М., служащий для измерения скорости снаряда, состоит из металлич. цилиндра, наполненного землей или песком и открытого с одного конца. Цилиндр помещается в раме, могущей качаться на призме О (фигура 10) около горизонтальной оси. Для измерения скорости υ снаряда последний направляют так. обр. чтобы он попал в цилиндр в горизонтальном направлении и там застрял. Измеряя угол отклонения а всей системы от положения ее равновесия при ударе снаряда, можно определить величину V следующим образом. В течение очень короткого, но конечного промежутка удара снаряда о баллистич. М. можно пренебречь всеми внешними силами (весом тела, реакцией опоры и тому подобное.) по сравнению с силами внутренними (смотрите Удар).

Обозначая расстояние от центра тяжести снаряда до оси вращения О через ί, а моменты инерции снаряда и цилиндра относительно той же оси через I я Г, имеем, применяя ко всей системе теорему о моменте количества движения (смотрите Механика теоретическая) и принимая во внимание, что сумма моментов внутренних сил равна нулю:

ωΐ + ωΐ — mvl=0, (38)

где co(I + I)—сумма моментов количества движения в конце удара, со—угловая скорость вращения всей системы в этот же момент, mvl—момент количества движения в начале уда- __тра и ж·— масса г снаряда. Для определения величины со, ВХОДЯ- Фигура 9. Фигура 10.

щей в уравнение

(38), применим теорему живых сил. В начале движения всей системы (в конце удара).

общая живая сила равна “² (I + J), а в конце движения равна нулю. Работа внешних сил, то есть сил тяжести снаряда и маятника, равняется

Mgd (cos а — 1) + mgl (cos α — 1), где Μ—масса Μ., d—расстояние от ц. т. его до оси О. Приравнивая приращение живой силы системы работе внешних сил, имеем:

— ψ{1+1)=Мgd (cos а—1)+mgl (cos a — 1), (39)

о

откуда

,=*(40)

Подставляя значение (40) в (38), получаем: 2sin“__________.

«-> _mVg(Md + ml)(l + r) (⁴¹)

Для измерений, не требующих особой точности, можно снаряд принять за материальную точку, так что в этом случае Г=т1². Величину I можно предварительно измерить упомянутым выше методом качания.

М., длительность полного размаха которого (полупериод) равняется 1 ск., называется секундным. Длина Я математического секундного М. определяется из уравнения (18), приняв ί=1:

Так как ускорение силы тяжести g зависит от географической широты φ места, то и Я есть функция φ. Наблюдениями установлена следующая функциональная зависимость Я от величины φ:

λ_φ=Д₄₅°- 0,002536 cos 2φ= 0,991026 +

+ 0,0050719 sin²?), (43)

где λ_φ·—длина секундного математич. М. в метрах на широте φ. Таким образом имеем: Яо°=99,103 сантиметров (наэкваторе), Д₄б°=99,3563 см, Яэо°=99,610 сантиметров (на полюсе). О конструкции и роли часовых маятников см. Часы. Горизонтальный маятник см. Сейсмические приборы и Колебательное движение. См. также Гравиметрия.

Лит.: см. Механика теоретическая; Эйхен-

вальд А. А., Теоретическая физика, ч. 2, М., 1930; О а 1 i 1 е х &., Discorsi, Leiden, 1638; нем. пер. «Ostwalds Klassiker d. exakt. Wissenschaft», Lpz., 11, p. 75—83; Huygens Ch., Horologium oscillato-rium, P., 1673; Euler L., Mechanica sine motus scientia, СПБ, 1736; Newton I., Philosophiae naturalis principia mathematica, 1687; «Enzykl. der mathem. Wiss.», B.—Lpz., 1901—08, B. 4, T. 1, Abt. 1, Heft 4, p. 504 (с библиографии, сведениями); Gray A., Treatise on gyrostatics and rotational motion, Theory a. Applications, L., 1918; M о u 1 t ο n F. R., «Rendiconti dei circolo mathematico di Palermo», Palermo, 1911, 33,-p. 338; Webster A.,The Dynamics ot particles, B.—Lpz., 1925; Gramm el R., Die mechanischen Beweise fiir die Bewegung der Erde, Berlin, 1922; Foucault L., Recueil des traveaux scientiiiques, Paris, 1878; Hagen I., La rotation de la terre, Rome, 1911; Giebel K., Das Pendel, Halle, 1928’. 1YI. Серебренников.