> Техника, страница 60 > Мембрана

Мембрана

Мембрана, диафрагма, очень, тонкая и совершенно гибкая пленка, растянутая между какими-нибудь опорами. М. может быть закреплена по некоторой замкнутой пространственной или плоской кривой, или частично по некоторым линиям, или в нескольких точках (минимум трех). Натяжение т М. на 1 см² м. О. различно в различных точках. Практически интересен и особенно полно разработан случай плоской М. с равномерным натяжением т по всей поверхности (смотрите статью Граммофон; натяжение там обозначено р и названо модулем упругости). В противоположность мембране, под пластинкой подразумевается плоское тело произвольного контура и некоторой толщины d, обладающее некоторой жесткостью, то есть сопротивляющееся изгибу. Коэф-т жесткости пластинки

N=—, где Е—модуль Юнга, s—плот ность и μ—коэф-т Пуассона.

Практически М. и пластинку трудно разграничить, ибо существует довольно постепенный переход от совершенных М. (мыльный пузырь, резиновая пленка) через М. с малой жесткостью (бумага, кожа, ткани, тонкие листди металла) к пластинкам в буквальном смысле слова (металлические и де-

ревянные пластинки, как то: деки музыкальных инструментов, гонги, «мембраны» электроакустических излучателей). Общепринятое название «мембрана» телефона, микрофона или граммофона, строго говоря, не точно, т. к. здесь мы имеем дело с пластинками довольно значительной жесткости. Закрепление пластинок м. б. различных родов: 1) неподвижное закрепление по замкнутой кривой, ограничивающей пластинку (например прочный зажим по окружности) или неподвижное же закрепление, но частичное по нек-рым незамкнутым линиям (например две стороны прямоугольника); 2) закрепление, подобное первому, но оставляющее свободу вращения около граничных линий (свободно опертые пластинки); 3) закрепление в одной или нескольких точках или областях конечной площади и наконец 4) совершенно свободная пластинка (практически трудно осуществимый случай).

Уравнение колебаний М. [^х]. Большой практический интерес представляют поперечные колебания М., находящейся под действием равномерного натяжения τ на 1 см². Если через w обозначить смещение М. от плоскости равновесия (ж, у), а через у> (ж, у, t) вынуждающую силу на 1 см² поверхности М., то для случая малых колебаний зависимость смещения w от ж, у и времени ί определится диференциальным уравнением:

, 9²w (d^vi. d³v>. f , _мч

^s · т - ^τ Ы + W) + ^ψ(*’ ^y’⁽¹⁾

где s—масса 1 см² поверхности М. Силы трения в этом уравнении не учтены. Величина с ^г,- определяет скорость распространения поперечных волн по М. Для случая собственных периодических колебаний М. (с круговой частотой со) получается, полагая ψ(χ, y, t)=О, уравнение:

дх²

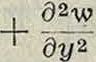
+ κ4ν=О,

(2)

В полярных координатах (г и <р)

где κ=₍уравнение это примет вид:

dw, 1

3²U 1

at-² "г _{r r2}

S+^=o.

(3)

Для случая статической нагрузки М. мы получим диференциальное уравнение упругой поверхности, полагая=0:

/92W дЯ²

или в полярных координатах для случая равномерной нагрузки Р на 1 см³: dvo Р

/d²-w. д²ч>., л

(^Г + 7S7iJ+V(®.»)-0

(4)

d²vo, 1 ~дг² г dr

(5)

Прямоугольная и квадратная М. [Ч. Общее решение ур-ия (2) для собственных колебаний прямоугольной мембраны со сторонами: а по оси ж и & по оси у имеет вид:

СО СО

w=2 2 ^cos "м⁴ +

h ^ 1 k .·= 1

_ · НпХ · /?.7iW /л

+ Bhlc^{sln ω}1Λ0 ^sin и " ’ ^sm ь "

Круговая частота обертона порядка h, к выражается следующей формулой:

(Онк=^у^Г% + ^г (7)

Суммирование производится два раза, а именно при каждом данном h производится суммирование по к от 1 до оо и затем все эти выражения суммируются при значениях h от 1 до аз. Постоянные А и В определяются из начальной формы М. при f=0 и из пограничных условий.

Если стороны а и Ь несоизмеримы, то при данных h и к каждый из множителей sin —~

и sin ^к*^у обращается в нуль при значениях координаты ж=α·” (η=1, 2,., h) или у=b _k (п=1, 2, ., к). При этих значениях ж и у получаются линии покоя, или узловые линии, па- _nv_j

раллельные сторонам прямоугольника. Если а и b соизмеримы, то могут возникать узловые линии более сложной формы. Этот случай резко выступает при α= Ь, то есть в квадратной мембране. В случае квадрата

frd-t

Фигура 1.

Яг“

Фигура 2.

Яо-З Фигура 3.

®М=“|^fW+k³, (Г)

откуда очевидно, что частота не меняется при перестановке чисел h и 7с; однако для решения w_hk и w_k1l получаются два различных выражения, налагающихся друг на друга. Подобные тоны М. носят название д в о й-

В=-со β=-2 В=-7 β=-±- β=

B=i~ β=7 β=2 β=οο

K=2, UJIU κ=1.

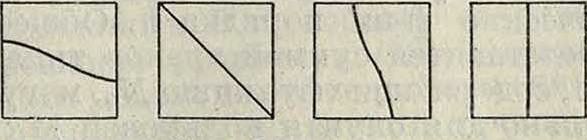
Фигура 4.

η ы χ тонов. Форма узловых линий для случая h=к=1; h=к=2; h=k=3 дана на фигуре 1, 2 и 3; в этих случаях Ник показывают число стоячих полуволн в направлении оси ж и оси у. Для случая h=1, fc= 2 или h=2, к= 1 получается одинаковая частота: о>₁₂=со₂₁=Vb, в ]/~ Р^аз большая, чем для основного тона ω_η. В этом случае две серии колебаний ео₁₂ и о>₂₁ налагаются друг на друга и выражение для w при частоте ω₁₂ м. б. приведено к виду:

w=A sin ^π“- · sin у [sin (со₁₂ ΐ + #₁₂) +

+ В sin (ω₁₂ + #2i)], (8)

где В—отношение амплитуд колебаний.

-Я-12

Уравнение узловой линии получим, приравнивая нулю выражение в скобках. Только при #21^12 или #2ΐ=^ΐ2+^π УР-ие узловой линии не содержит время t и получаются устойчивые узловые линии (фигура 4 и 5).

В общем же случае узловая линия в течение периода изменяет свой вид, проходя через все формы, указанные на фигуре 4, и единственной точкой покоя (узел) является центр. Картина узловых линий для

β——со в=-г в=- e=~j- в-о

/)=/, к=3,.или_Л /7=3, к=/,

frrze-f

B=j- β=1 В=2 в=°°

ο

Ο 0

Фигура 5.

двойного тона, при h= 1 и при 7г=3 или при h= 3 и ie=l, дана на фигуре 5. В табл. 1 дается с [⁴] обертонов квадратной М. в первых трех октавах, принимая высоту основного тона за 1.

Таблица 1,—Обертойы квадратной М. в первых трех (I, II, III) октавах.

I II III

2,000	8,000	4,000	5,000	6,000	7,000
2,286	3,162	4,123	5,099	6,042	7,071
2,550	3,536	4,301	5,148	6,083	7,106
	3,606	4,472	5,385	6,325	7,211
	3,808	4,528	5,523	6,403	7,280
		4,743	5,701	6,519	7,382 i
			5,831	6,671	7,517
				6,708	7,616
				6,964	7,649
					7,810
					7,906

Круглая М. Отдельные члены решения ур-ия (3) для круглой М. (смотрите Граммофон) [*] даются выражением:

w=А_Л sin ()ιφ + φ₀) [I_h (xr) +

+ i_hNb (κτ)] sin (xot + #), (9)

где I_h и N_h—бесселева и нейманова цилиндрические ф-ии порядка h. Общее решение представится суммой членов типа (9). Члены, содрржащие функцию N_h, могут входить только для случая кольцевой М.; для круговой М. параметр λ должен быть равен нулю. Постоянные А_р, Яр, κ и <р₀ определяются из граничных условий и начальной формы М.; число h определяет число узловых диаметров (смотрите Граммофон, фигура 10); при данном h параметр частоты κ может иметь целый ряд значений в зависимости от числа (внутренних) узловых кругов р. Важный прак-тич. случай колебания М., зажатой по окружности радиуса R и не имеющей узловых диаметров, соответствует 7ι=0, 1=0, и ур-ие колебаний принимает вид:

№=^Aloixr) sin (xct +&), (10)

причем κ принимает следующий ряд значений [²]:

2,405

5,52.

*“-ΊΓΪ

8.65

*3=- _гу- и Т. Д.

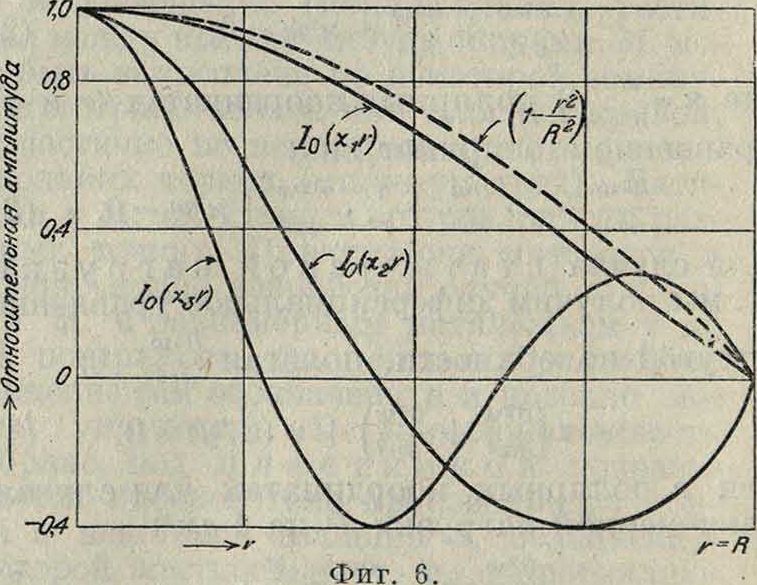
Форма М. при колебаниях (при трех первых значениях параметра κ) приведена на фигуре 6. Колебание при основном тоне (и_г), как видно из чертежа, очень близко к форме упругой поверхности М. при статической равно мерной нагрузке Р на 1 с.и²; в этом последнем случае из ур-ия (5) получается ур-ие упругой поверхности:

где

А

PR 2 4τ

(11)

Период основного колебания круглой М. равен

При наличии коэф-та трения <5 (на 1 см²) высота основного тона

ψ-ay· <*>

Высоты обертонов в первых трех октавах даны в таблице 2, причем высота основного тона принята за 1.

Таб.тг. 2,—В ысогн с о б с т в тонов круглой К.в первых трех октавах (I, II, III).

I	II		III
1,00	2,13	3,15	4,06	5,07	6,02	7,06
1,59	2,29	3,50	4,13	5,12	6,15	7,18
	2,65	3,60	4,22	5,42	6,154	7,31
	2,92	3,65	4,60	5,53	6,21	7,40
			4,61	5,54	6,48	; ,4-i
			4,83	5,66	6,52	7,50
			4,90	5,97	6,67	7,60
					6,74	7,66
					6,83	7,86
					6,94	7,89

Плоские М. более сложной формы. Имеются теоретич. исследования М. кольцевых, эллиптических параболических, секторовид-ных [³]. Гельмгольц применил теорию секторовидной М. к исследованию колебаний «основной» М. лабиринта уха [⁴].

Применения М. Благодаря легкости, М. обладают большим коэф-том затухания,

что обусловливает .размытость резонансной кривой. При частотах значительно ниже основного тона М. дают относительно одинаковую амплитуду под действием вынуждающей силы любой частоты. Для конденсаторного микрофона (смотрите), сконструированного Венте [⁵], применяется например М., настроенная выше 16 000 колебаний в ск., и поэтому все частоты в области речи и музыки передаются микрофоном почти без искажения. М. применяются в целом ряде звукоприемников,

например: фонодейк Миллера [*], мембраны военных звукометрических станций и др. В музыкальных инструментах М. применяется в барабане (кожа). Барабанная перепонка уха есть М., близкая к конической форме, причем натяжение ее неравномерно, в виду чего законы ее колебания весьма сложны [⁴].

Поршневая М. [⁷]. Под этим названием подразумевают плоский совершенно негибкий поршень, колебания которого происходят в направлении нормали к его поверхности, причем он движется весь как одно целое. Такого типа М. очень важна теоретически, т. к. для нее легко рассчитать излучаемую мощность. Практические М. и пластинки разных типов в отношении излучения стремятся свести к эквивалентной поршневой М. (смотрите Звук). М. поршневого типа применяются в новых типах громкоговорителей (Blatthaller—Сименса и Гальске). В телефонах типа Брауна поршневая мембрана имеет вид конуса, сделанного из очень тонкого алюминия; в центре она возбуждается электромагнитным способом, края ее соединены при помощи тонкого бумажного кольца с круглой оправой; весь конус колеблется как одно целое.

Конические М. (фигура 7) очень распространены в различных типах громкоговорителей; чаще всего их делают из толстой бумаги (тип «Рекорд» и другие) и они имеют диаметр наружного отверстия в несколько десятков см. Конич. мембрана может колебаться как одно целое только при самых низких частотах, при более высоких на ней образуются стоячие волны, затухающие от центра к окружности [⁸].

Пластинка [*]. Диференциальное уравнение колебаний плоской пластинки для случая малых колебаний (при отсутствии затухания) будет 4-го порядка:

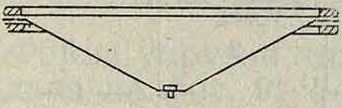
Фигура 7.

--- + N ( 0(2 ^ Ч.

У d*vo ^ дх“ду ²

ду

y=9(x,y,t),(HY)

где s—плотность, d—толщина пластинки; N—коэфициент жесткости и ψ(χ, у, t)—вынуждающая сила на 1 см² поверхности пластинки. Собственные колебания подчиняются уравнению:

d² v

Ίη*

+ W-

cHw Ox

) d*w дх’ду²·

+

dy*

H’

(14)

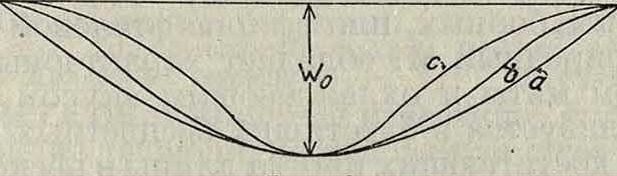
где

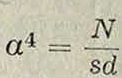
_ E((2 J2s(l-ii2)

(15)

Для случая периодических колебаний круговой частоты ω уравнение (14) распадается на два уравнения 2-го порядка:

d² v дх² d² v дх²

где **-.·£ (16)

Первое из них тождественно с ур-ием М. [²], второе разнится от него знаком при κ², то есть интеграл его получится из интеграла ур-ия (2) заменой я через гя, где г= V—I· Полный интеграл уравнения (1б) составится из суммы отдельных решений, умноженных каждое на произвольную постоянную. Строгое решение ур-ий (16) м. б. проведено только для круглой пластинки [*]. Для собственных колебаний круглой пластинки получится из (16) в полярных координатах два ур-ия:

0² гч. 1 0w, 0га л" Г‘ дг Л"

,0²W

± я²У)=0.

(17)

Ур-ие упругой поверхности при статич. нагрузке пластинки определится из диферен-циального ур-ия:

d* v _{( 0} d*vo. d*v? ψ(χ, у, t) ~дх^ ‘ ^ дх“ ду“ ^ ~ду“ ~ N

(18)

Квадратная пластинка. Удовлетворительное решение уравнений (16) для квадратной пластинки получено Ритцем в 1909 году [⁹] при помощи рядов. Это решение, гораздо более сложное, чем для М., исследовано Ритцем для случая совершенно свободной (незакрепленной) квадратной пластинки. Форма узловых линий для простейших обертонов дана на фигуре 8. 4-й по

/г/г,4з к‘2б,4о к’Злго λ=βο,β

Фигура 8.

высоте обертон является двойным тоном (смотрите выше—квадратная М.) и для него узловые линии меняют свою форму в течение периода; на фигуре 8 даны для этого случая узловые линии в два разных момента периода. Высоты собственных тонов квадратной пластинки определяются из формулы:

<¹⁹⁾

Значения λ для 4-х первых обертонов (для μ =0,225) даны на чертеже. Изучение колебаний квадратной пластинки имеет гл. обр. теоретический интерес и практич. применений не имеет. Опытное исследование колебания пластинки произведено Хладни [¹⁰]; по его имени именуются сложные фигуры узловых линий, получающиеся при колебаниях пластинки. Упругая линия прямоугольной пластинки, нагруженной равномерным давлением Р и свободно опертой по краям [решение уравнения (18)] выражается сложным рядом, первое приближение которого (практически достаточно точное) [“]:

Ра“

^w=т

4 +.

лЬ

sh^:

th ^:

, лb ей. — 2 а

-ch—

(20)

Круглая пластинка f¹]. Для этого важного практически случая уравнение собственных колебаний (17) решается вполне строго при помощи цилиндрич. ф-ий: w=A sin (hq> + φ_α) [I_h(xr) + λI_h{ixr) +

+ X’N_h(xr) + X"N_h(vcr)J sin (я²аЧ + &). (21) Так как функции N_h(0) при любом h обращаются в оо, то для круглых пластинок следует положить V=λ"=0. Для кольцевых пластинок Я и λ" конечны. Для совершенно свободной круглой пластинки [¹²] основной тон соответствует колебаниям с образованием двух узловых диаметров (1г=2, р=0). Два более низких тона, соответствующие

Я=0 и h=1, при р=0 возникнуть не могут. Более высокие обертоны образуют такого же вида узловые линии, как и для М. (смотрите Граммофон, фигура 10). Высота тона обертонов определяется по формуле:

4 (xR)²d __ Е гоо

I 4лД2 У 3s(l — Л*²)

Для очень высоких обертонов получается приближенно [*] (Калене):

xR=(h+2p)”·

Для первых обертонов значения (1-я

Хоризонтальная строчка) и относительную высоту тонов (2-я горизонтальная строчка) дает табл. 3 (д при вычислении принято равным 0,25).

Таблица 3.—3 начения ( ^ ) ^{и 0 тонн 11 0 с и} ’^{г е л ь}"

нал высота тонов для совершенно свободной круглой пластинки.

h	0	1	2	3	4	5
РX
0			1,38	3,187	5,58	8,54
	—	—	1,00	2,31	4,05	6,20
1	2,222	5,102	8,22	13,29	18,45	24,29
	1,613	3,70	6,40	9,64	13,39	17,63
2	9,584	14,93	21,09	28,00		_
	6,96	10,84	15,31	20,33
3	21,91 15,90			_	_	_
			~

Радиусы узловых кругов (отличны от таковых ясе для круглой мембраны) даны в таблице 4 (а также и для μ=0,25). Для круглой пластинки, закрепленной в центр е, возможны все виды колебаний

Таблица 4.—Р адиусы узловых кругов для совершенно свободной круглой пластинки.

	0	1	2	3	4	5
1	0,609	0,781	0/821	0,845	0,861	0,873
2	0,391 0,842	0,498 0,871	0,560 0,887	0,604 0,899	-	-
3	0,257	—	—	—	—	—
	0,591	—	—	—	—	—
	0,894	—	—	• —	—	—

с любым числом узловых колец р и диаметров h. Соутвелл [^,3] вычисляет параметр частоты (xR) для случая различных радиусов (6) внутреннего зажимающего круга; для Ь=0 параметр xR дан в таблице 5. Частоты

Таблица 5.—Значения параметра *Д.

	0	1	2	h Р >4	0
0	1,937	(0—1,2)	2,35	2	7,79
1	4,573			3	10,94

обертонов вычисляются по формуле (22) (сталь, /4=0,3). Случай пластинки, закрепленной в центре, интересен практически для изучения колебаний в турбинах, прядильных машинах и т. и.

Круглая пластинка с зажатым наружным краем имеет большое практическое значение в электроакустике. Диференциальное уравнение (17) колебаний имеет для нее решение [¹⁴]: w=A sin (h<p + φ₀) [I_h(xr) +

+ ZI_/t(ixr)] sin (x²a4 + #). (23)

Параметр частоты (xR)=z определится из трансцендентного ур-ия, получаемого из граничных условий гр,. _{= л}=0 и ⁼ 0^;

Ш (²⁴)

Частота f_hp находится по ур-ию (22). Значение параметра частоты z=xR (1-я горизонтальная строчка) и относительные частоты (2-я строчка) для круглой пластинки, зажатой по окружности, приведены в таблице 6[¹⁶]; в скобках даны соответственные значения для круглой М.

Таблица 6. — Значения параметра z и относительной частоты для круглой пластинки с зажатым наружным краем.

h РХ^	0	1	2	3
0	3,196	4,611	5,906	7,143
	1,00 (1,00)	2,08 (1,59)	3,41 (2,13)	β,ΟΟ (2,65)
1	6,306	7,799	9,197	10,537
	3,90 (2,29)	5,96 (2,92)	8,30 (3,50)	10,87 (4,06)
2	9,439,	10,958	12,402	13,795
	8,72 (3,60)	11,74 (4,22)	15,03 (4,83)	18,70 (5,42)
3	12,577_ 15,50 (4,90)	14,108	15,579	-
		19,50 (5,53)	23,70 (6,15)

Для обертонов высших порядков параметр z приближенно вычисляется по ф-ле: z=[h+ +2(p+l)j · Радиусы узловых кругов даны в таблице 7 (в скобках те же радиусы для М.).

Таблица 7.—Величины радиусов узловых кругов.

X	0 1	2	7ι p	0
1	0,38 (0,44) 0,49 (0,55)	0,54(0,61)	3	0,19
2	0,26 (0,28). 0,35	_		0,44
	0,58 (0,64) 0,64	-		0,68

Высота основного тона круглой пластинки, закрепленной по краям (fe=0, р=0),

/о,о=0,47^|Л _йД₂₎· (25)

Для железной пластинки (Е=2 · 10¹² —; μ=0,28; s=7,8)

/о,о=0,25 · 10⁶=10⁶

(D—диаметр пластинки, d—толщина пластинки). Опытное исследование колебаний круглых пластинок сделано Шульце [¹⁶].

Пластинки сложной формы. Плоские пластинки прямоугольной формы по методу Ритца, а также пластинки ромбические, трехугольные и эллиптические исследовали Е. Гольдман [¹⁷], Шуллер [¹⁸], и Терада [¹⁹].

Криволинейные пластинки. Релеем разработана теория цилиндрич. и шаровых пластинок [*]. Много исследований посвящено колебаниям колоколов. В колоколах при колебаниях образуются узловые линии двух типов: одни—сечением плоскостями, проходящими через ось, другие— перпендикулярно оси. Колокола применяются для получения сильных звуков в воздухе и под водой [²⁰].

Статическая нагрузка круглой пластинки, зажатой на краях. Ур-ие упругой линии для статической нагрузки (18) имеет для случая равномерной нагрузки Р г/см² решение:

— «9

для случая точечной нагрузки Р в центре пластинки Г²¹]:

w

16π1Υ V

7*2

R*

• TL

Да

(27)

Форма упругой линии для статич. нагрузки дана на фигуре 9; b—вычислено по формуле (26), с—по формуле (27), причем максимальные откло-

М о п

Фигура 9.

нения в центре w₀ (стрела прогиба) приняты равными. Для сравнения приведена форма упругой линии для М. (а).

Вынужденные колебания пластинки исследованы для круглых пластинок Дебаем [²²] и Франке i.²³]; случай мембраны телефона изучен Кеннеди и Тэйлором [²⁴] и Крэндаллом ί²⁵]. Теоретически этот вопрос чрезвычайно сложен. Для случая возбуждения с частотою значительно ниже основного тона, задача решается с удовлетворительным приближением при помощи ур-ий для статич. нагрузки (26), (27) и амплитуды различных точек пластинки при колебаниях соответствует фигура 9. Колебания кристаллических пластинок исследованы Фохтом [²⁶].

Лит.: р Rayleigh, Theory ol Sound, 3 ed., v. 1, chapt. 9 и 10, L., 1929; К a 1 a h n e A., Hand-buchd. Physik, hrsg. v. H. Geiger u. K. Scheel, B. 8, t>. 216—260, B., 1927; Miiller-Pouillets, Lehr-buch d. Phvsik, 11 Aufl., В. 1, T. 3, p. 186—206, Brschw., 1929; ³) Crandall, Theory ot Vibrating Systems a. Sound, v. 1, L., 1927; ³) Voigt W., «Getting. Nachrichten», Gottingen, 1907, P- 17 1 u. 34 1; Mathieu E, «Liouvilles .Tourn.». P., 1868, p. 137; ReinsteinE. «Ann. d Phys.», Lpz., 1911, Folge4, B. 35. p 109; ⁴) H e 1 m li о 11 7. H., Die Lehre von den Tonempfindungen, 6 Aufl., Braunschweig, 1913; ») Wente E., «Phys. Rev.», N. Y„ 1922, s-ries 2, v. 19, p. 498;·) Miller D., Science of Musical Sounds, p. 78, N. Y., 1922; ) A i g n er F., Unterwasserschall-iechnik, p. 114, B., 1922; ^s) Wagner K., Wiss. •Griindlagen d. Rundfunkempfang, p. 136—139, B., 1927; ⁹) R i e t z, «Ann. d. Phys.», Lpz., 1909, B. 28,

p. 737; >°) Chladni, Akustik, Lpz., 1802; ⁿ) NA-dai A., Elastische Platten, B., 1925; ^,!) Kirel-li off G., «Journ. f. relneu angew. Mathematik» (Crel-les Journal), B., 1850, B. 40, p. 5 I;¹³) South well R.,«Proc. of the Royal Soc. of London». L., 1922,111 A, p. 133; ^1J) Rayleigh, Th ory of Sound, v. 1, § 221a, L., 1-929; “) C a r r i n g t о n, «The Phil. Magazine a. Journ. of Science, L., 1925, si r. 6, p. 1261; ”) S c h u 1-7. e F., «Ann. d. Phys.», Lpz., 1907, B. 24, Folgi 4, p. 785; ·’) Goldmann E., Inaugural-Diss., Breslau, 1918; ^Ia) Schuller A., «Ann. d. Plrvs.», Lpz., 1908, B. 32, p. 245; “) Terada T., ibid., p. 509; •°) Aigner F., Unterwassprschallt chnik, p. 1, 6, 8, 44,-146, 265, Berlin, 1922; ²¹) N & d a i A., Elastische Platten, В., 1925, p. 56 u. 61; ^M) Debye, «Ann. d. Phys.», Lpz., 1908, B. 25, Folge 4, p. 849; “) Fran-ke G., «Ann. d. Phys », Lpz., 1929, Folge 5, B. 2-, p. 649; ³‘) Kennel у a. Taylor, «Proc. of the Amrr. Philos. Soc.», Philadelphia, 1905, v. 44, p. 96; “)C r a n d a 11, «Journ. of the Am»r. Inst. Electr. Eng.», N. Y., 1921, v. 40, p. 791; ³») Voigt W., «GrOtt. Nachr.», Getting n, 1915, p. 345; ^ST) Giebe E. u. S c h e i b e A., «Jahrbuch d. drahtlosen Telegr. u. Teleph.», B., 1930, B. 35, p. 16§. С. Ржевкин.