Механизмы

Механизмы, системы тел, в которых перемещение одного тела (ведущего) вызывает совершенно определенные перемещения остальных тел системы. Одно из тел механизма рассматривается при этом как неподвижное и перемещения остальных тел определяются относительно этого неподвижного тела, называемого стойкой; остальные тела М. называются звеньями М. Обычно в состав М. входят твердые неизменяемые тела, но встречаются М., в состав которых входят растягиваемые гибкие тела (ремень, канат, цепь) или жидкости под давлением. Изучением состава М., путей различных точек их, скоростей и ускорений этих точек занимается прикладная механика в узком смысле этого слова, или кинематика М. Вместе с возникновением прикладной механики как науки (1800 г.) вырабатывается классификация М., основанная сначала на принципе «превращения движений и преобразования скоростей». В книге Виллиса [¹] эта классификация получила свое завершение. Классификация Виллиса сохраняется в нек-рых учебниках прикладной механики и до сих пор; в ее основу положена мысль о том, что назначением М. является преобразование величины или направления скорости движения, причем упускаются из виду остальные кинематич. элементы движения— путь и ускорение. Виллис различает три случая изменения соотношений величины и направления скорости ведущего и ведомого звена: 1) соотношение направлений и величин скоростей остается постоянным; 2) соотношение направлений остается постоян ным, соотношение величин скоростей изменяется; 3) соотношение направлений движения М. изменяется, соотношение величин скоростей либо изменяется либо сохраняется постоянным. Соответственно этим трем случаям различаем 3 класса М.: 1-й класс— клин, винт, цилиндрич., конич. и гиперболо-идальные зубчатые и фрикционные колеса, червячная передача, групповые приводы и эпициклические приводы зубчатых колес, передачи гибким телом (ременная, канатная и цепная), гидравлич. передача и тому подобное.; 2-й класс—некруглые зубчатые колеса, колеса с неполным числом зубцов, гуков шарнир, нек-рые шарнирные М., и прочие; 3-й класс— кулачные М. и большинство шарнирных М. Классификация Виллиса обладает значительными недостатками; в основу ее положен случайный признак — соотношение скоростей; один и тот же тип М., например шарнирный четырехзвенный М. при одном соотношении длин звеньев оказывается во 2-м,при другом— в 3-м классе; в один и тот же класс входят М. самой различной структуры как плоские, так и пространственные; научно-механич. исследование М., расположенных по классификации Виллиса, требует многократных повторений и вообще отличается бессистемностью; классификация Виллиса совершенно не приспособлена к исследованию более сложных М., например шарнирных с числом звеньев более четырех. Поэтому ее нужно считать устаревшей.

Труды Р е л о [²], особенно Бурместе-р а [³], дали принятую в современной науке классификацию М., которая в основных чертах основывается на структуре М. Согласно этой классификации, кинематику М., как и всю теоретич. кинематику, разделяют на кинематику плоских М. и кинематику пространственных М. Пути всех точек звеньев плоского М. располагаются в одной плоскости или в плоскостях взаимно параллельных, без искажения проектирующихся на плоскость чертежа; кроме того и относительная траектория, то есть путь какой-нибудь точки одного подвижного звена относительно плоскости или пространства, неразрывно связанных с другим подвижным звеном, есть также плоская кривая, расположенная в плоскости чертежа. Пути точек пространственного М. могут быть плоскими или пространственными кривыми (например сферическими); во всяком случае пути эти не должны лежать во взаимно параллельных плоскостях или относительные траектории их не должны быть .плоскими кривыми или располагаться во взаимно параллельных плоскостях. Примером пространственного М. может служить пара конических зубча-• тых колес; каждое колесо вращается вокруг своей оси и его движение—плоское, однако плоскости движения шестерни и зубчатки не параллельны между собою, а относительные траектории, на изучении которых основано правильное профилирование зубцов, суть сферич. кривые (смотрите Зубчатые колеса).

Первым этапом в изучении М. является знакомство с кинематич. парами, то есть с простейшими кинематическими сочленениями, которые разделяются на низшие и высшие сочленения. Низшие

сочленения плоских М. суть: цилиндрич. шарнир и ползун; низшие сочленения состоят из стойки и подвижного звена и обладают свойством обратимости; это значит, что если подвижное звено превратить в стойку, то от этого кинематич. характеристики (пути, скорости и прочие) не изменятся. Четыре звена, соединенные между собою шарнирами или ползунами, представляют собою простейший шарнирный М., известный под именем четырехзвенной цепи, или четырехзвенного М., или четырехшарнирного М., или шарнирного четырехугольника. Высшие сочленения плоских М. образуются непосредственным соприкосновением двух тел. Примером высшего сочленения двух тел является неприменяемое в машиностроении сочленение дугового двуугольника в равностороннем тр-ке (фигура 1), обладающее одной степенью свободы,т.к. при

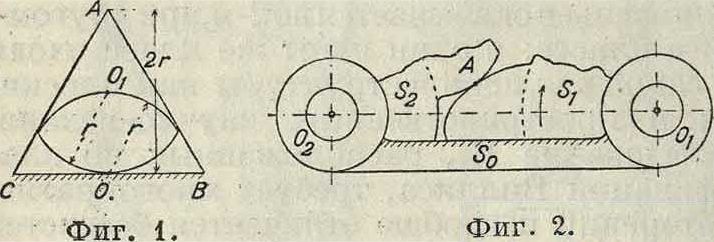
всяком положении двуугольника имеем три точки касания; чечевицеобразный вырезок OO_t, ограниченный двумя цилиндрич. поверхностями радиуса г, катится без скольжения по одной грани полой равносторонней призмы АВС, сечение которой имеет высоту 2 г, скользя ребрами по двум другим граням. В машиностроении распространено другое высшее сочленение (фигура 2), состоящее из трех звеньев: стойки 0₂0, с двумя цилиндрическими шарнирами и двух звеньев S, и S₂, которые совершают вращательные движения. Эти звенья соприкасаются в точке А, и ведущее звено, наир. S_lt заставляет двигаться ведомое непосредственным соприкосновением передающих движение профилей, причем один профиль скользит по другому; передача движения прекращается, когда профили перестанут соприкасаться; такое сочленение, или такая кинематич. пара, в которой передача движения не вполне обеспечена, называется незамкнутым сочленением или п а-ройс неполными связями. Для обеспечения принужденного движения должен быть приняты какие-либо меры для замыкания цепи; наиболее Фигура з. распространенным явля ется замыкание с ил о й,например для замыкания сочленения (фигура 2) при ведущем звене S, вращающемся по часовой стрелке, достаточно снабдить звено S₂цилиндрич. барабаном с намотанным на него гибким телом, к концу которого подвешена гиря, обеспечивающая прижимание S₂ к S_x. Б кулачковых М. (смотрите Кулак) замыкание производится пружиной; в зубчатых колесах (смотрите) профили зубцов двусторонни, и, если сделать зазор достаточно малым, то

система имеет полные связи. Групповые приводы из зубчатых колес и эпициклич. приводы являются примерами сложных М.,образованных из высших сочленений.

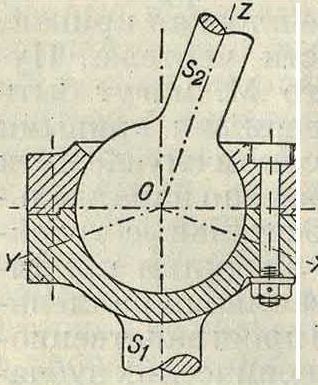
Для сочленения пространственных М. служат часто те же элементы, что и для плоских: цилиндрич. шарнир, ползун, передача непосредственным соприкосновением, но иногда применяются и особые пространственные сочленения: 1) цилиндрический ползун в полом цилиндре, имеющий две степени свободы—поступательное движение вдоль оси цилиндра и вращение вокруг нее; 2) шаровой шарнир (фигура 3), имеющий три степени свободы—вращение вокруг неподвижной точки О, слагающееся из трех вращений вокруг взаимно перпендикулярных осей ΟΧ, ΟΥ, OZ; 3) винт и гайка (смотрите Болт)—сочленение, имеющее только одну степень свободы, обладающее свойством обратимости и потому относимое к низшим сочленениям.

Итак, при помощи соответственных сочленений можно получить простые М., плоские

.1 |L

Фигура 4.

или пространственные. Из всего многообразия возможных при этом комбинаций Рело первый подметил общие черты при кажущемся разнообразии форм и этим указал простейшие пути образования новых М. без увеличения числа звеньев. Если изображать М. схематически, то часто два на вид различных М. имеют тождественные схемы и следовательно представляют собой один и тот же М. Отметим следующие часто встречающиеся методы преобразования М.

1) Изменение стойки. Как пример рассмотрим прежде всего схему М. зубчатого зацепления (фигура 2); если неподвижно звено S₀, то имеем обычную зубчатую передачу; если сделать неподвижным одно из зубчатых колес S, или S₂, получим схему М. эпици- фигура 6.

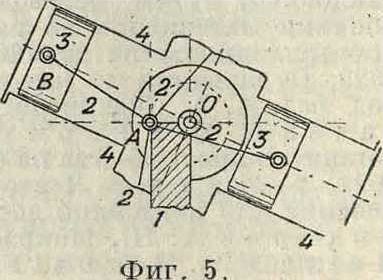
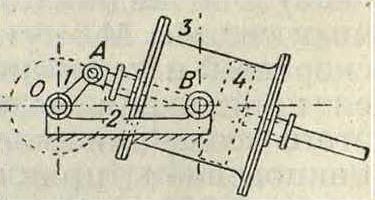
клич, привода. Еще ярче можно иллюстрировать возможное разнообразие на кривошипном механизме (смотрите Кривошипный механизм). На фигуре 4 изображена схема кривошипного механизма обычной поршневой машины (двигателя или насоса) простого действия; стойкой служит звено 4 прямолинейной направляющей. На фигуре 5 изображен тот же кривошипный механизм в схеме авиационного двигателя «Гном» со звеном 1 в качестве стойки и с несколькими цилиндрами (изображено их схематично два), вращающимися вокруг оси О. Наконец в схеме пароходной машины с хгачающимся цилиндром 3 (фигура 6) стойкой служит звено 2, кривошип 1 попрежнему приводит во вращение коренной вал, а пор-

шень 4 с поршневыми скалками совершает сложное движение.

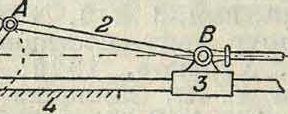
2) Замена коромысла кулисой и обратно. Всякое коромысло, то есть звено, вращающееся вокруг неподвижной оси и совершающее неполный оборот, м. б. заменено

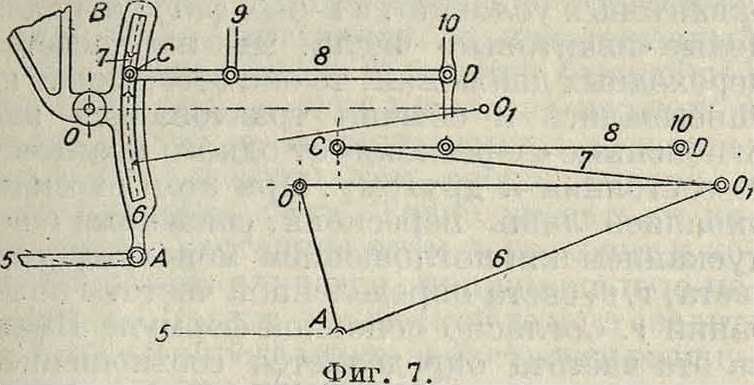
кулисой, то есть круговым ползуном,—отрезком цилиндрич. кольца, скользящим между двумя цилиндрич. поверхностями. Для примера на фигуре 7 кулиса ОАВ реверсивного парораспределения Гейзингера, очень распространенного в современных паровозах, е плотно ходящим в ней ползуном С заменена на схеме в нижней части фигура 7 неизменяемым тр-ком АОО_г (звено б), а ползун (камень 7) заменен звеном СО_г.

3) У ш прение шипов и изменение размеров звеньев. Внешний вид М. может быть изменен до неузнаваемости изменением размеров звеньев. Так например,если в кривошипном М. (фигура 4) увеличить размер шипа О звена 1 настолько, чтобы его

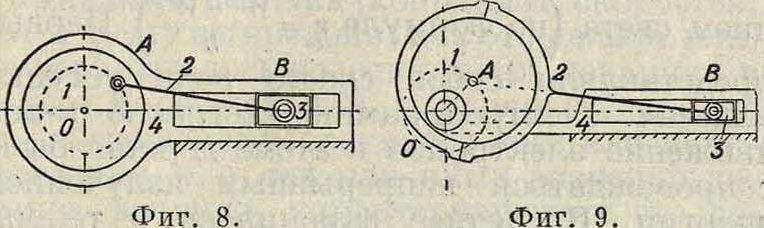
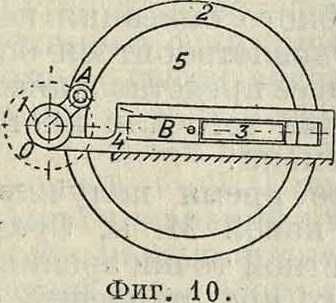
радиус стал больше радиуса кривошипа, то получим М., изображенный на фигуре 8. Если подобным же образом увеличить размер шипа 1, то получим изображенный на фигуре 9 эксцентриковый М., составляющий весьма важную часть большинства распределительных М. На фигуре 10 изображен ползун 3 и жестко связанный с ним диск 5, центр которого находится в В; при движении ползуна по его направляющей центр В движется вместе с ползуном вдоль направляющей. Диск охвачен кольцом 2, к-рое шарнирно сочленено с пальцем А кривошипа J, вращающегося вокруг неподвижной оси О. Этот М. получен следовательно увеличением размеров шипа В. На фигуре 11 изображен тот же

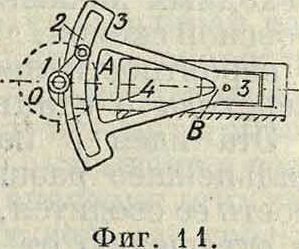
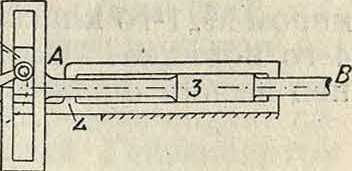
кривошипный М. (фигура 4), но звено 3 снабжено кулисой радиуса А В, а шатун АВ превращен в маленький ползун этой кулисы (камень 2). Наконец на фигуре 12 представлен случай, когда кулиса прямолинейна, то есть когда радиус А В бесконечно велик; но АВ есть длина эквивалентного шатуна кривошипного М., следовательно на фигуре 12 изображен кривошипный М. с бесконечно длинным шатуном.

Перейдем теперь к самой трудной части— классификации многозвенных шарнирных М.

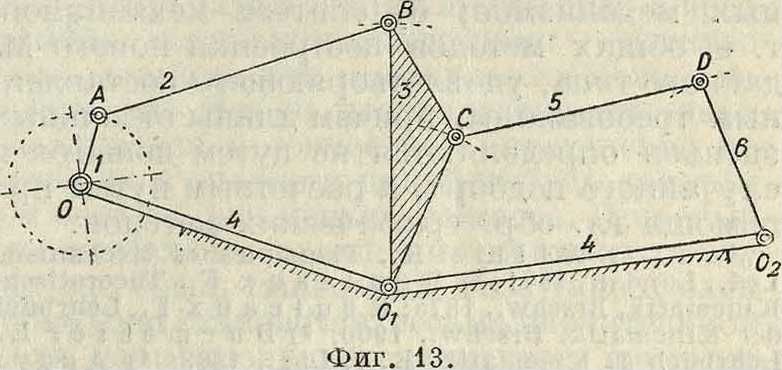
Здесь можно отметить ряд неудачных iА предложений, например: шарнирные М. т с числом звеньев более четырех объединить под общим названием—сложные шарнирные М.; или сложные шарнирные М. разделить на шести-, восьми-, десятизвенные механизмы и т. д. Такая классификация чисто формальна и не облегчает работу исследования. Наиболее рациональной из предложенных надо признать классификацию сложных шарнирных М., предложенную проф. Л. В. Ассуром [⁴]. Рассмотрим обычные методы увеличения числа звеньев шарнирного М., исходя из простейшего четырехзвенного (фигура 13); для этого проще всего взять еще два звена 5 и б, соединенных шарниром (двухповодковую группу),и сочленить звено 5 с какой-либо точкой, например С, одного из трех подвижных звеньев, например 3. Звено б присоединим шарнирно к какой-либо точке, например 0₂, стойки; анализируя добавку к основному четырехзвенному М., замечаем, что она представляет собою также четырехзвенный М. OfiBOi, кинематич. исследование которого представляет собой повторение методов исследования М. ОАВОЕсли бы звено 5 было шарнирно присоединено к какой-либо точке звена .2, то это также не осложнило бы исследования. Прибавляя к полученному М. еще сколько угодно раз по два звена, можем создать М. с каким угодно большим числом звеньев, не осложняя его

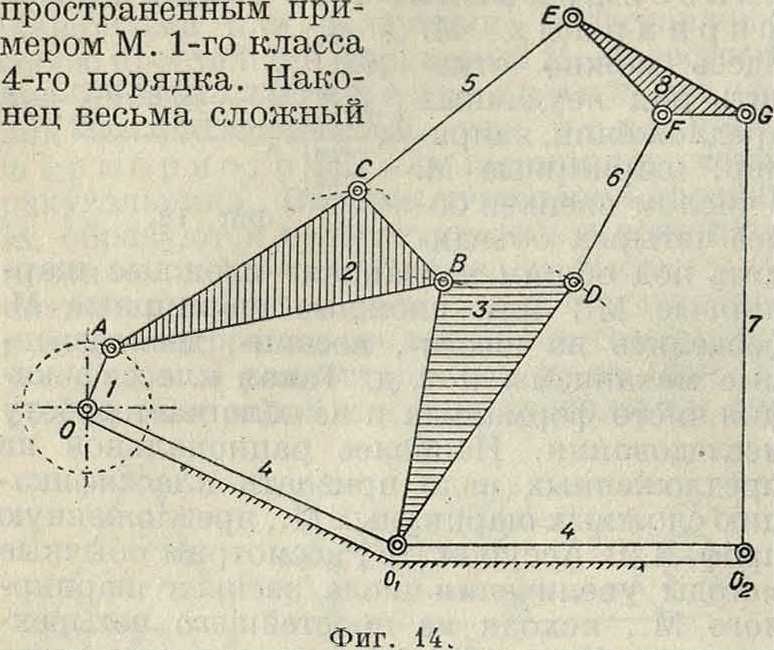
исследования. Осложнения начнут возникать только тогда, когда к М. присоединим трех поводковую группу (фигура 14), состоящую из одного трехшарнирного звена EFG (звена 8) и. трех поводков 5, б и 7, сочлененных шарнирно с различными движущимися или неподвижными звеньями М., в данном случае с движущимися точками С и D и с неподвижной точкой 0₂. Согласно классификации, предложенной Л. В. Ассуром, простые разомкнутые М., образованные присоединением групп различной сложности, суть М. 1-го класса, которые, смотря по наиболее сложной группе сочленения, входящего в них, подразделяются на порядки. Большинство применяемых в машиностроении

М. суть М. 1-го класса 2-го порядка. Кроме того можно отметить ряд М. 1-го класса 3-го порядка, а именно кулисные М. сист. Стефенсона, Гуча и Аллана, т. к. они содержат одну или две трехповодковые группы. М. кулисы Гейзингера содержит четырехповодковую группу и является весьма рас-

М. кулисы, изобретенной русским машинистом Савельевым, относится к М. 3-го класса 6-го порядка. Кроме совершенно новых и оригинальных методов кинематического исследования этих весьма сложных М. в работе Л. В. Ассура намечены также пути образования самых сложных шарнирных М. (замкнутых цепей) и указаны методы графич. построения скоростей и ускорений их точек.

В новейших трудах [⁵] германских ученых по теории М. (Грюблер, Альт и др.) кроме очерченных выше задач анализа М. (структура, пути различных точек, их скорость, ускорения, центры кривизны путей, центры скоростей, центры ускорений и прочие) поставлены в общем виде и новые задачи: а) кинематики и динамики пространственных механизмов; б) синтеза механизмов, то есть общих методов построения нового М. · данного типа, удовлетворяющего поставленным требованиям, причем длины отдельных звеньев определяются не путем попыток и случайного подбора, а расчетным путем при помощи гл. обр. графических методов.

Лит.: ) Willis К., Principles of Mechanism, led., London, 1841; 2) Reuleaux F., Theoretische ICinematik, Brschw., 1875; Reuleaux F., Lehrbuch dor Kinematik, Brschw., 1900; ³)Burmester L., Lehrbuch d. Kinematik, В. 1, Lpz., 1888; ⁴) Accyp Л. В., Исследование плоских стержневых механизмов с низшими парами с точки зрения их структуры и классификации, «Известия С.-Петербургского политехнич. ин-та», СПБ, 1913, т. 20, стр. 329—3S5 и 581—635, 191 4, т. 21, стр. 187—283 и 475—573; 5) «Ζ. d. VDI», 1927, р. 164, 1928, р. 1933; Зернов Д.С., Прикладная механика, Л., 1925. К. Рерих.