> Техника, страница 61 > Механика квантовая

Механика квантовая

Механика квантовая, или волновая, представляет собой дальнейшее развитие теории квантов (смотрите), созданной Планком, Эйнштейном и в особенности Бором, который применил ее к строению атомов и молекул. При этом Бор ввел представление о двух типах физич. процессов: процессов стационарных, соответствующих определенному «состоянию» атома (или молекулы) и образующих некоторое прерывное многообразие, и процессов переходных, представляющих собой переходы от одного состояния к другому. В теории Бора стационарные состояния описывались при помощи обыкновенной «классической» механики, причем энергия, момент количества движения и другие постоянные движения фиксировались при помощи определенных «квантовых условий», в которых фигурировали целые «квантовые» числа. Что же касается переходных движений, то они совершенно не описывались и обычно трактовались как мгновенные «перескоки» от одного квантового состояния к другому. При этом рассматривались лишь перескоки, связанные с испусканием или поглощением монохроматич. света, то есть света определенной частоты колебаний г. Согласно основной формуле Планка эта частота определяется соотношением

V =, где W и W" — энергии началь ного и конечного состояний, a h= 6,55·10^-27 эрг/ск.—постоянная Планка. Эта формула в связи с представлением Бора о квантовых стационарных состояниях дала возможность расшифровать закономерности в строении спектров атомов и молекул и на основании этих спектров определить энергию, а также другие константы движения, характеризующие их стационарные состояния.

Переходные движения делились на два типа: 1) самопроизвольные (или «спонтанные»), сопровождающиеся испусканием света, то есть уменьшением энергии атома, и 2) вынужденные, могущие сопровождаться как испусканием, так и поглощением света (по формуле v=^V--_h^1V j. Первые представляли собой своего рода уступку классич. электродинамике, согласно которой движение электронов в атоме должно было сопровождаться непрерывным излучением энергии. Последнее заменилось, в теории Бора рядом перескоков вниз по энергетической лестнице через одну или сразу через несколько ступеней, и, лишь достигнув наи-низшей ступени, соответствующей «нормальному» состоянию, атом успокаивался и переставал излучать. Однако из нормального состояния он мог перейти в одно из высших или «возбужденных» состояний под действием света надлежащей частоты колебаний.

Существенно отметить то обстоятельство, что теория Бора не только не описывала переходных движений, но не давала никакой возможности установить причину или момент их наступления или окончания. Это обстоятельство ощущалось многими физиками как. неполнота теории Бора. Лишь в 1917 году Эйнштейн предложил отрешиться от попыток более подробного описания переходных движений и удовлетвориться воровской схемой, дополнив ее представлением о вероятности наступления того или иного перехода в единицу времени.

Эта идея в настоящее время получила дальнейшее развитие в новой М. к. Сущность ее сводится, с известной точки зрения, к отрешению от обычных представлений о. движении не только в случае движений «переходных», но и в случае движений «стационарных», то есть следовательно в случае вообще всякого вида движений, и к замене этих представлений, связанных с точным пространственно-временным описанием соответствующего движения, некоторой вероятной схемой последнего. Для лучшего уяснения смысла этой схемы рассмотрим сначала вкратце применение ее к переходным движениям. Представим себе атом, находящийся в начальный момент в некотором и-ом стационарном состоянии и подверженный действию излучения. В течение ближайшей единицы времени атом может перескочить в любое другое m-ое стационарное состояние как с поглощением, так, вообще говоря, и с испусканием света. Точно указать, в какое именно состояние атом перескочит и когда именно это случится, принципиально невозможно. Задача физической теории сводится только к определению вероятности различных мыслимых переходов п-+т, спонтанных или же вызванных излучением. Эти вероятности могут быть определены и экспериментальным путем, если рассматривать не один атом, а множество одинаковых атомов или же множество экземпляров одного и того же атома, находящихся в начальный момент ί=0 в одном и том же п-ом состоянии. Вероятность перехода п-^т за данное время может быть при этом измерена относительным числом атомов (или экземпляров), перешедших за это время в состояние т.

Совершенно аналогичным образом трактуются в новой М. к. стационарные и всякие другие движения. Вместо того чтобы определить ход движения, то есть описывать непрерывное изменение характеризующих его динамич. величин (координат, скоростей, сил и т. д.) во времени, как это делала или, вернее, пыталась делать старая механика и теория Бора, новая М. к. ставит себе задачу об определении вероятности того или иного состояния, то есть тех или иных значений динамич. величин, характеризующих это состояние в функции времени. При этом предполагается, что одному и тому же начальному состоянию могут соответствовать, вообще говоря, любые конечные состояния. Это предположение находится на первый взгляд в полном противоречии со всеми нашими представлениями о детерминизме физических явлений как об однозначной определенности следствий причинами или конечного состояния начальным. Рассматриваемое противоречие смягчается однако тем обстоятельством, что новая М. к. исключает возможность точной характеристики состояний в том смысле, как это делается старой механикой. Так например, исследуя движение материальной частицы, например электрона, в данном «внешнем» силовом поле (например вокруг положительного ядра атома), старая механика фиксирует состояние частицы заданием шести величин: трех координат частицы х, у, г и трех проекций ее скорости v_x, v_y, и_гдля некоторого начального момента времени {=0. При этом путем интегрирования уравнений движения оказывается возможным точно определить значения этих величин для любого последующего или предыдущего момента времени. Таким образом вероятность состояния, определяемого этими значениями,при данном исходном состоянии оказывается равной единице (вероятность «1» означает достоверность), а вероятность всякого другого значения — равной нулю (невозможность).

Если М. к. не знает этих двух крайностей —· достоверности и невозможности — и считает все конечные состояния возможными (хотя и не одинаково вероятными) при одном и том же начальном состоянии, то это по крайней мере отчасти объясняется тем, что рассматриваемые «состояния» (как начальное, так и конечное) фиксируются ей не вполне определенным образом. Этот принцип неопределенности (в характеристике состояний), впервые вскрытый Гейзенбергом в 1927 г. (уже поеле формулировки основных законов М. к.), может быть формулирован в простейшем случае следующим образом: чем точнее ф иксируется положение материальной частицы, тем менее точно может быть определена ее скорость, и, наоборот: чем точнее фиксируется скорость частицы, тем менее точно м. б. определено ее положение. В своем обосновании принципа неопределенности Гейзенберг исходил из анализа экспериментальных условий, в которых происходит наблюдение движения материальных частиц. При этом он отметил тот факт, что всякое наблюдение частицы, имеющее целью определение ее положения, неизбежно связано с нек-рым воздействием на нее (например воздействием света, если наблюдение осуществляется визуально), к-рое вызывает неконтролируемое изменение скорости частицы в момент наблюдения; аналогичным образом воздействие, требуемое для измерения скорости, неизбежно вызывает неконтролируемое изменение положения.

Естественно возникает вопрос: если дело обстоит таким образом, то почему же физики этого раньше не замечали? Ответ весьма прост: раньше физики занимались изучением макроскопических явлений, в которых участвуют большие количества материи и энергии; принцип же неопределенности, формулированный выше, дает себя чувствовать-лишь в том случае, когда имеют дело с чрез вычайно маленькими частицами — электронами, атомами или молекулами. Можно показать, что степень неопределенности, вкрадывающаяся в совместное определение положения и скорости какой-нибудь частицы, тем больше, чем меньше ее масса. При обычных массах она совершенно ничтожна, в случае же очень маленьких масс (масса электрона) она становится весьма значительной. Если например координата х частицы измеряется с точностью Аж (то есть заключена между х и ж+Аж), то неконтролируемое изменение в скорости v_x частицы, по оси X, вызываемое измерением ж, лежит (приблизительно) в пределах Av_x=^- · так что Дж-Д»_ж=^_. Здесь

h обозначает постоянную Планка, т—массу частицы. Для электрона т=9 10^-28 г, и следовательно Дж · Δг>_хз=1, между тем как для частицы с массой в 1 г Дж · Av_xsi 10~²⁷.

Величины, которые нельзя одновременно точно измерить, называются (канонически) сопряженными. Подобную сопряженную пару образуют между прочим энергия и время. Отсюда следует, что, фиксируя энергию атома в каком-нибудь стационарном состоянии, мы тем самым лишаемся воз можности говорить о времени, к к-рому относится то или иное положение электронов в атоме или, другими словами,—о конфигурации этих электронов в данный момент времени.

Итак, задача М. к. как учения о поведении элементарных частиц материи заключается в определении вероятности тех или иных состояний или событий в мире этих частиц, то есть тех или иных значений величин, характеризующих эти состояния или события, при определенных значениях других величин, которые могут быть одновременно измеренными, и характеризующих условия, при которых исследуется рассматриваемая система частиц. Решение этой задачи было найдено еще до того, как она была правильно поставлена, и притом двумя совершенно различными путями. По одному пути, проложенному Бором, к этому решению, в несколько схематической форме, пришел Гейзенберг, отчасти в сотрудничестве с Бором и Иорданом. По другому пути, который был намечен еще в 1905 г. Эйнштейном, к нему пришли де-Бройль и Шредингер. Этот последний путь на первый взгляд не имеет ничего общего с рассматриваемой проблемой и относится к совершенно другой стороне квантовых явлений, которой в теории Бора уделялось очень мало внимания,—именно к вопросу о природе излучения, испускаемого (или поглощаемого) атомами при переходе из одного состояния в другое. Тот факт, что испускание и поглощение света осуществляется не непрерывным образом, а в виде отдельных «актов», был установлен Планком еще в 1900 году. Планк же установил основное соотношение ε=Τιν между энергией e=W— W", теряемой (или приобретаемой) атомом, и частотой v—испускаемого (или поглощаемого) света. Сосредоточив свое внимание на атомах, Бор вывел отсюда свое представление о существовании прерывного ряда стационарных состояний. Эйнштейн же, сосредоточив свое внимание на испускаемом или поглощаемом свете, пришел к мысли о прерывной корпускулярной структуре последнего. Таким образом Эйнштейн вновь возродил ньютоновскую теорию света как потока частиц особой «световой субстанции». При этом однако для характеристики этих частиц Эйнштейн исходил уже не из ньютоновской механики, а из им же самим (в том же 1905 г.) установленной механики, теории относительности, в которой масса какой-либо частицы не является постоянной величиной, но зависит от скорости v ее движения по отношению к наблюдателю по фор-мулет=———, где т₀ — так называемая

ν-%

«покоящаяся» масса (при υ=0), а с—скорость света. Для «световых» частиц, движущихся по определению со скоростью v=с, масса т может иметь конечное значение только в том случае, если «покоящаяся» масса т_аравна нулю. Этим свойством, с точки зрения теории Эйнштейна, отличаются световые частицы, или кванты, от частиц обыкновенной материи (для которых ж₀>0). Отсюда следует, что световые частицы имеют эфемерное существование, ограничивающееся временем их полета от одного атома, которым они испускаются, до другого атома, к-рьш они поглощаются; в первом они «рождаются» за счет его энергии, а во втором погибают, превращаясь в его энергию.

Согласно эйнштейновской механике, частица массы т обладает (собственной) энергией ε=тс² и количеством движения д= mv. В случае световых квантов, v=c и д=тс,

то есть д=—. Полагая, по Планку, ε=hv и принимая во внимание, что c=v, где λ—длина волны света (с точки зрения волновой теории), мы получаем 0=^, или, заменяя длину волны волновым числом=равным числу волн в 1 см, подобно тому как v=ψ равно числу периодов в 1 ск. _гмы получаем соотношения:

ε=h v и д=h к. (1)

Второй особенностью эйнштейновской теории света, отличающей ее от теории Ньютона и непосредственно выраженной в предыдущих соотношениях, является неразрывная связь корпускулярных представлений с волновыми. Введя представление о световых лучах как о потоке световых квантов, Эйнштейн отнюдь не отбросил прежнего представления о них как о линиях распространения световых волн, но пытался трактовать оба представления как два различных аспекта одного и того же физического явления. При этом соотношения (1), характеризующие «качество» света (то есть частоту колебаний, или длину волны, с волновой точки зрения, и энергию, или количество движения квантов, с корпускулярной), были дополнены им следующим вполне естественным соотношением, характеризующим «количество», или интенсивность, света: концентрация световых квантов, то есть число их п в единице объёма, пропорциональна квадрату амплитуды ψ₀ световых колебаний в соответственной точке:

η ~ ψ₀. (2)

Двойственность представлений, введенную А. Эйнштейном в учение о свете, долгое время тщетно пытались устранить. Если такие явления «классической» оптики, как интерференция (смотрите) и диффракция (смотрите) света, находились в противоречии с корпускулярным представлением о свете, то ряд новооткрытых явлений, как например фотоэлектрический эффект, эффект Комптона (смотрите Рассеяние света) и т. д. находились в совершенном противоречии с волновым представлением и, наоборот, весьма естественным образом интерпретировались с точки зрения корпускулярной теории, и только через 20 лет после появления ее Л. де-Бройль в 1925 году впервые понял, что корпускулярно-волновой дуализм, введенный А. Эйнштейном в учение о свете, неустраним, что он является новым фундаментальным принципом физики и что он должен относиться не только к свету, но равным образом и к обыкновенной материи.

Простейшими элементами материи являются электроны. В свободном состоянии электроны наблюдаются в виде катодных лучей

(смотрите Лучи корпускулярные). Со времени их открытия в конце 90-х годов и вплоть до 1925 года катодные лучи трактовались как корпускулярное явление, то есть как поток частиц, летящих от катода (отрицательного полюса) разреженной трубки. Де-Бройль дополнил это корпускулярное представление волновым, предложив рассматривать катодные лучи как особого рода волны, аналогичные световым, и связав частоту v и длину

λ=-j этих «катодных волн» с энергией ε=тс²

и количеством движения g=mv соответствующих частиц (электронов) теми же самыми соотношениями (1), которые были установлены Планком и Эйнштейном для света. Определяя произведение νλ=ιυ как скорость распространения катодных волн, мы получаем для нее формулу w — ^. Таким образом волновая скорость оказывается обратно пропорциональной корпускулярной. Длина волны катодных лучей, вычисленная по формуле де-Бройля для лучей, обычно при меняемых на практике, оказывается такого же порядка величиной, как и для рентгеновых лучей. Отсюда естественно было ожидать, что при отражении катодных лучей от кристаллов или прохождении их через очень тонкие пленки кристаллич. или микро-кристаллич. вещества должны получаться такие же интерференционные и диффракци-онные явления, как и в случае рентгеновых лучей. Это предсказапие теории блестяще подтвердилось в опытах Дэвисона и Джер-мера, Г. П. Томсона, Е. Руппа и др. В ча- » стности Руппу удалось наблюдать диффрак-циот катодных лучей от обыкновенной оптич. диффракционной решетки, причем измеренная им длина волны в точности совпадала с теоретической. Заметим, что скорость катодных лучей v м. б. вычислена из разности потенциалов V, примененной для их ускорения, по ф-ле: кинетическая энергия с² · т — с² · т₀=в²

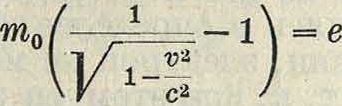
У,

где е—заряд электрона. В случае не слишком быстрых катодных лучей (υ мало в сравнении с с) точное, релятивистское выражение для кинетической энергии можно заменить обычным Imv², что дает (mv)²=2meV, и следовательно

Я=·

yzmeV

Выражая V получаем:

в вольтах, а λ

JM

w

в ангстремах,

Предыдущая формула представляет собой частный случай связи менаду длиной катодных волн и потенциальной энергией соответствующих частиц. Обозначая через W полную энергию одной из частиц, а через U (ж, у, г)—по-енциальпую энергию ее в точке (ж, у, г), имеем ~ =W—U я так. обр.

Распространение световых волн в какой-нибудь прозрачной среде определяется ди-ференциальным ур-ием:

, β³φ. дц> __ i _ дЦ,.

дх² ду“ dz² w²·αt² ’ ^

где ψ представляет собой колеблющуюся величину (например электрическое напряжеЕше), a w—скорость распространения волн в данном месте. В случае монохроматич. колебаний зависимость ψ от времени выражается множителем е~^г2лН (или cos2nvt, или же sin2?№{), так что ~=— 4π²ν²ψ. Замечая,что

v 1 _//4Ч

—=д, получаем в этом случае вместо (4):

(5)

Это «волновое» ур-ие, установленное для световых волн, было по аналогии распространено Шредингером в 1926 году на волны де-Бройля. Подставляя в (5) выражение (3) для длины их как функции координат, получаем таким образом основное ур-ие Шре-дингера:

д“у. дх²

Вопрос о физич. смысле волновой функции Ψ, фигурирующей в этом ур-ии, был выяснен несколько позднее Борном. По аналогии с соотношением (2) для световых волн можно было бы рассматривать квадрат амплитуды колебаний, то есть квадрат абсолютного значения (модуля) ψ, как меру числа электронов в единице объёма вблизи данной точки. Эта интерпретация вполне естественна в том случае, когда ур-ие (0) применяется к б. или м. интенсивным катодным лучам, то есть к большому числу электронов, при условии конечно, чтобы действием их друг на друга можно было пренебречь, ибо потенциальная энергия Ό(χ, у, г) характеризует лишь действие внешних сил на электрон, находящийся в точке (ж, у, г). По существу однако ур-ие (0) должен быть применимо и к предельному случаю «одного катодного луча», образованного движением одного электрона в заданном внешнем силовом поле. В этом случае величину |ν»|², то есть квадрат модуля функции ψ, следует трактовать, согласно Борну, как меру вероятности нахождения электрона в соответствующей точке. В случае большого числа экземпляров электрона, не действующих друг на друга, относительное число электронов в объёме dV=dx-dy-dz должно 6е>еть пропорционально вероятности I ψ !² dV нахождения одеюго из них в этом объёме. С этой точки зрения волны .материи оказались волнами вероятности. Вместе с тем оказался решенным и вопрос о фактич. определении вероятности, по крайней мере в простейшем частном случае, к к-рому относится шре-дингеровское ур-ие (6), то есть в случае движения одной частицы с постоянной энергией в постоянном (не зависящем от времени) силовом поле.

Решения ур-ия (6) имеют вид:

гр=у>° (ж, у, z) · е^г2лг1, (!)

где частота v=^m°^c^⁺ — представляет собой «волновую» меру энергии движения (в слу-

чае покоящейся частицы эта энергия сводится к постояннойт₀ · с²).Вероятность,или,вернее, «объёмная плотность» вероятности v>j²===|yi°|², не зависит следовательно от времени. То обстоятельство, что время не входит в характеристику движения, непосредственно связано с точным определением энергии последнего. Во многих случаях ур-ие (6) допускает регулярные решения, то есть такие решения, для которых функция ψ остается конечной, однозначной "и непрерывной для всех значений х, у, z, лишь при определенных дискретных значениях энергии W. Эти дискретные значения (образующие бесконечный ряд) или, вернее, связанные с ними функции у>, и соответствуют «стационарным движениям» или «квантованным состояниям» теории Бора. В других случаях значения W и ф-ии Ψ образуют непрерывный ряд, соответствующий ряду движений непериодического характера, которые в теории Бора вовсе не рассматривались. Так например, в случае электрона, тяготеющего к неподвижному положительному заряду с потенциальной энергией U=—^Zp (г—расстояние и Z—атомный номер), квантованным эллиптическим движениям соответствует дискретный ряд энергий:

W_n=-²^^^m (»-1, 2, 3, .—«главное квантовое число») с волновыми ф-иями вида:

Г

y>³=fn-i(r) е ~ап · у_е(в, φ),

ll 2

ίη—ι полином (w-l)-fi степени, a=—

радиус первой квантовой орбиты теории Бора, а y/β, φ)—шаровая ф-ия 1-го порядка (1=0, 1, — 1) от углов Θ и φ, опре деляющих направление радиуса-вектора г]. Гиперболическим движениям электрона соответствует непрерывный ряд энергий W от О до оо, с непрерывным рядом ф-ий у>, изображающих (набольшихрасстояниях) стоячие шаровые волны определенной длины.

К важнейшим обобщениям и дополнениям предыдущих результатов относятся: а) Н е-стационарные процессы. Если в уравнении (6) заменить множитель W при ψ эквивалентным ему в виду (7) оператором з!> ^{то оно} приобретает вид:

д²у>. д“у, д²у> Алгт дх² ду² "И дг². h

8л²т _{ТТ Л}

- *г νψ-Ο.

(8)

Это уравнение представляет собой непосредственное обобщение ур-ия Шредингера (6), применимое к случаю движения частицы в переменном силовом поле (зависящем от времени). Отметим, что это ур-ие по своей форме существенно отличается от обобщенного волнового уравнения (4). В частном случае постоянного силового поля общее решение ур-ия (8) имеет вид:

Ψ =2 ^СЛ> (9)

П

где ψ_η—частные решения вида (7), то есть вида:

г2л ₂

Ψη=Ψ°η (®, У, 2) ^{е h m}°^C”

W_n)t

Коэфициенты с_п в (9) характеризуют относительные вероятности соответствующих стационарных состояний. Нормируя ф-ии ψ_ηсогласно условию J ψ„² dV=1, мы получаем в силу свойства «ортогональности» этих ф-ий (ортогональность ф-ий ψ_η и у_т выражается равенством нулю интеграла J y>„y>_m dV)

J W?dV=Y_i |c„:².

Т. о. при условии 2 Ю=1, величину |с_п ² можно трактовать как вероятность и-го состояния (при любом положении частицы).

Квадрат модуля ψ получается умножением этой ф-ии на величину, с ней комплексно сопряженную ψ, то есть получающуюся из нее заменой i=V— 1 на —г. Имеем следовательно:

ψ:²= 2 Κί²Λΐ² +

η

i2nW_n-W_m.

+ 2 S ^h (¹⁰)

n=f=m

T. о. «плотность вероятности» слагается в рассматриваемом случае из ряда постоянных членов и из двойного ряда членов, гармонически колеблющихся с частотами: _v _ W_n-W_m

^vn,m _h · ·

(11)

Согласно теории Бора этой ф-лой выражается частота света, испускаемого или поглощаемого электроном (атомом) при переходе из n-το состояния в т-е (илинаоборот). С волновой же точки зрения v_{n m} представляет собой как бы частоту «биений» между п-м и т-м колебаниями при одновременном их «звучании». Исходя из этого обстоятельства, Шредингер попытался восстановить классич. (волновую) теорию испускания и поглощения света, заменив точечный электрон волновым электроном, электрич. заряд которого распределен в пространстве с объёмной плотностью, пропорциональной ψ ²=ψψ. Эта точка зрения не может считаться вполне правильной; однако в известных пределах она позволяет весьма просто интерпретировать квантовые законы излучения. Прежде всего из нее непосредственно следует, что, находясь в определенном стационарном состоянии, электрон не может давать излучения, т. к. при этом он эквивалентен объём-номуэлектрич. заряду с постоянной во времени плотностью. Далее интенсивность излучения, испускаемого при суперпозиции двух колебаний, соответствующих двум разным стационарным состояниям пят, оказывается пропорциональной сумме квадратов модулей величин

Хп,т=f ΧψηΨηι dV и т. д. (12)

Этот результат приводит в простейших случаях к «правилам отбора», найденным полу-эмпирич. образом в теории Бора. Величины типа (12) называются матричными элементами (или компонентами) величины х по отношению к рассматриваемым состояниям. Совокупность этих элементов образует матрицу, заменяющую в М. к. «классическую» величину х.

Гейзенбергу удалось формулировать законы М. к. независимо от Шредингера и несколько ранее последнего, совершенно не вводя волновой функции и пользуясь исключительно матричными элементами различных величин. Заметим, что с корпускуляр-

ной точки зрения одновременное осуществление двух различных стационарных состояний с разными энергиями (W_n и W_m) представляется немыслимым. Соответственно этому испускание света частоты», ,, должно трактоваться ей как результат перехода из и-го состояния в т-е (или наоборот). Матричные элементы x_Ki,_nили, вернее, квадраты их абсолюта, значений являются с этой точки зрения мерой вероятности подобных переходов. Что касается вынужденных переходов, связанных с поглощением или испусканием света или же с какими-нибудь другими возмущающими действиями, то их вероятность определяется квадратом абсолютных значений матричных элементов той дополнительной энергии, к-рою характеризуется это возмущение, по отношению к соответствующим невозмущенным состояниям (или, вернее, волновым функциям, их характеризующим). При п=т матричные элементы представляют собой среднее значение соответствующей величины в состоянии п=т. б) Переход к обычной (классической) механике. Предыдущие результаты относятся не только к элементарным частицам материи—электронам, но и к сколь-угодно сложным частицам, поскольку можно отвлечься от их внутреннего строения и трактовать их как материальные точки с определенной массой т. Поведение системы подобных «точек» характеризуется уравнением:

С у ~(—Y °² + ϋ + ϋι л.

[в“* oyl ‘ о4 ‘

+ и(х_и ?д,«!,., х_п, у_п, г_п - А ψ=0. (13)

Если положить в нем

· 2 лЗ

ψ — е ^ίι, (14)

то оно приобретает вид:

_ XI ^h /d²S I 92S, d*S

_ду β*ϊ)

β=1

Если для всех рассматриваемых частиц от-

h

ношение —· очень мало, как это имеет место

Щг для частиц обыкновенной материи, то первой суммой в левой части предыдущего уравнения можно пренебречь. При этом оно сводится к известному диференциальномуур-ию Гамильтона-Якоби:

iiKS’+dr+din+f+n-o.ae)

к — 1

в к-ром ф-ия & представляет собой т. н. «действие». Это уравнение описывает движение множества экземпляров рассматриваемой системы в координатном пространстве х₁₉.z_n при этом «плотность» множества (соответствующая вероятности ψ ²) не играет существенной роли, т. к. из него всегда оказывается возможным выделить один определенный экземпляр и проследить за его движением с помощью соотношений:

dxjc dS dyjf. dS dzk OS

dt dxk*

I]. — >

“ dt 0щ

^m* Ail ~

dt dzi_c

(17)

определяющих скорости частиц данной системы в произвольно избранной ее конфигурации. В случае ур-ия (15) подобное точное определение скорости при данной конфигурации оказывается невозможным, причем мерой неопределенности является для каждой частицы отношение ~ (ср. Гейзенберговский «принцип неопределенности»). Поэтому оказывается невозможным и выделение одного какого-либо экземпляра из всего континуума,—и, вместо того чтобы следить за движением подобного экземпляра, мы оказываемся вынужденными ограничиться определением относительного числа экземпляров, находящихся в заданной конфигурации, то есть, другими словами, вероятности этой конфигурации Что касается скоростей, то им соответствуют в волновой механике «операторы»

V=^р4* - ^{h 9 Р}*У ^{h д},.

^к’^х mjc Znimic дх_п ’ т“ 2та-т“ дук ’ " * ’

определяющие «вероятные значения» этих скоростей («математические ожидания») по формулам:

Vjc.x=- · Jv y>)dv₁. dv„. (18)

Аналогичными формулами определяются вероятные значения всех других динамически величин, характеризующих рассматриваемую систему. Все эти величины представляются в волновой механике, вообще говоря, диференциальными операторами (наир, оператор энергии); в частном случае операторов «нулевого порядка» получаются простые множители при у> (как наир, в случае координат или потенциальной энергии).

Лит.: Гааз А., Волны материи и квантовая механика, пер. с 2 нем. изд., М.—Л., 1930; Ш редин г е р Э., Принципы волновой механики, «УФН», М.—Л., 1928, т. 8; Д а р р о у, Волновая механика, там же, 1929, т. 9; Гааз А., Основания квантовой химии, перевод с нем.,М.—Л., 1930; Иордан П., Гипотеза световых квантов, «УФН», М.—Л., 1930, т. 10; Френкель Я., Происхождение и развитие волновой механики, «Природа», Л., 1930, январь; Frenkel J., Einfiihrung In die Welleamechanik, В., 1929; S ommerleU A., Wellenmechanischer Erganzungs-band z.um «Atombau undSpektrallinien», Braunschweig, 1928; В ornM.u. Jordan P., Elementare Quanten-mechanik, Berlin, 1930; Thirring H. und H a 1-pern O., Prinzipien der Welienmechanik, «Ergeb-nisse der exakten Naturwissenschalten», Berlin, 1928, B. 7, 1929, B. 8; Jordan P., Die Liciitquantenhypo-these, «Ergebnisse d. exakten Naturwissenschalten», Berlin, 1928; de В г о g 11 e L., Introduction a la mechani-que ondulatoire, 1929; Wey 1 H., Gruppentheorie u. Quantenmechanik, Lpz., 1928; Heisenberg W., Die physikalischen Prinzipien d. Quantentheorie, Leipzig, 1930; Dirae P. A., Quantenmechanik, Leipzig, 1930. Я. Френкель.