> Техника, страница 61 > Механика прикладная

Механика прикладная

Механика прикладная, наука о машинах, механизмах и сооружениях, основанная на принципах теоретической механики. Задача М. и. в этом более узком смысле • состоит в том, чтобы предсказать, как будет происходить то или другое движение части механизма или машины, какие пути будут описывать их отдельные точки и как велики будут у них скорости и ускорения. На основании полученных величин можно сделать. заключение о тех силах, которые необходимы, чтобы увеличить или уменьшить кинетич. энергию механизма или машины. Если присоединить сюда еще исследование влияния внешних сил, ускоряющих или задерживающих движение той или другой части машины, то тем самым будет дан первый очерк явлений,

с которым имеет дело М. п. в том объёме, какой подразумевается под этим наименованием в СССР. М. п. отличается от теоретической механики по своему методу тем, что в большинстве изучаемых ей вопросов не имеется математически точной зависимости одних величин от других, а потому нельзя применить строгого математического анализа, и приходится довольствоваться графическими построениями с целью дать разрешение поставленной задачи.

За последние 30 лет целый ряд выдающихся ученых (Гартман, Виттенбауер, Тол-ле и др.) дали образцы графич. построений, позволяющих с большой точностью и в то же время с большой простотой и ясностью выявить особенности задач из области М. п. Разберем в виде первого примера те явления, какими сопровождается работа пневматического зубила (фигура 1 и 2), положив в основание исследования диаграмму (фигура 3) пути по времени, записанную на быстро вращающемся барабане штифтом, прикрепленным к поршеньку, дви-

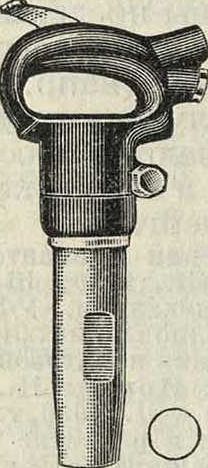
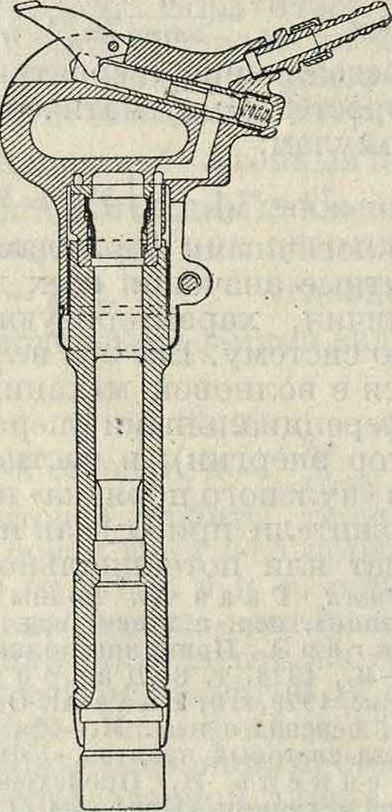
Фиг." i.

Фигура 2.

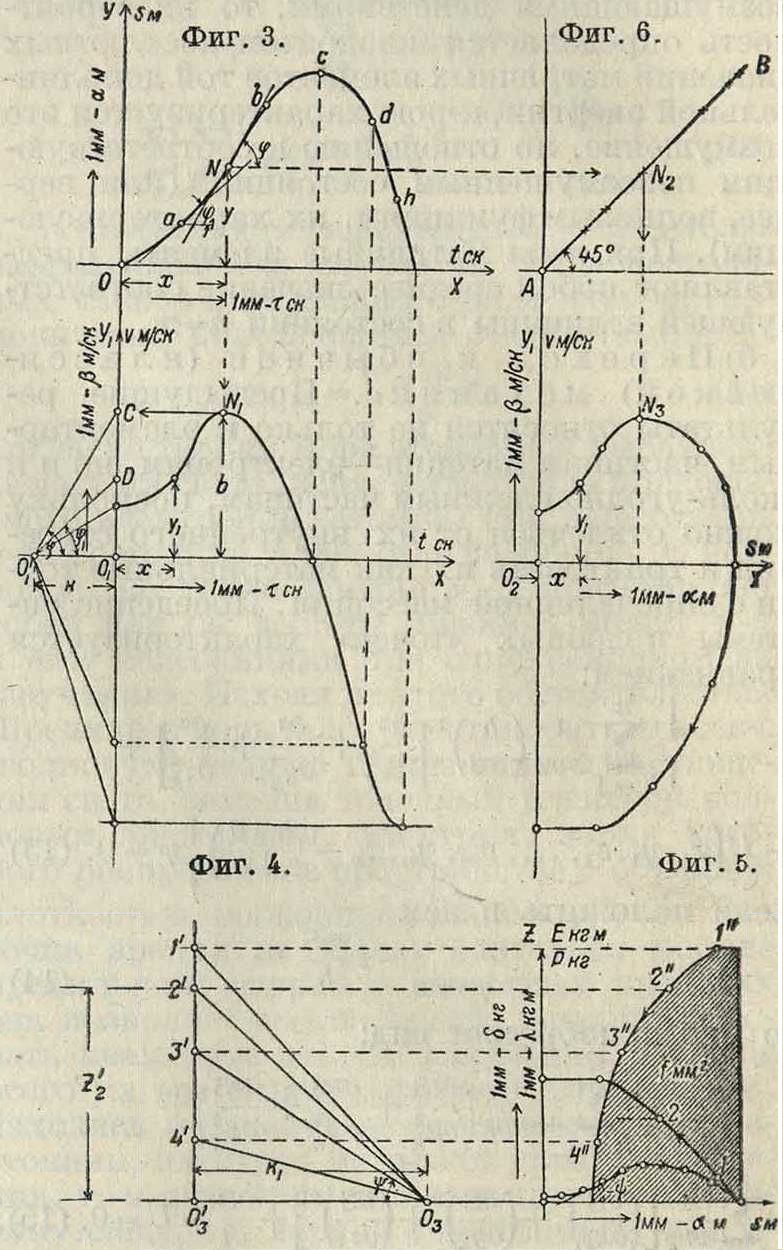
гающемуся в цилиндре под влиянием сжатого воздуха. Диаграмма (s, ί) имеет масштабы: по оси ординат 1 миллиметров—а м и по оси абсцисс 1 миллиметров—т ск. Проводя в точках О, а, b, с d и h касательные к кривой, получаем соответствующую величину скорости поршенька в м/ск:

ds а V=,1 I =

dy

dt τ dx r ^tg<P Максимальная скорость при подъеме поршенька будет в точке перегиба N кривой. Примем, что эта скорость выражена на диаграмме (фигура 4) отрезком Ь миллиметров, и построим эту диаграмму, отложив на оси ординат отрезок О_хС=Ь и проведя через точку С параллель к касательной в точке N к кривой st до пересечения с осью абсцисс в точке 0[. Из тр-ка С0[0₁ имеем: О_хС=U₁0₁ tg φ, или b=k tg φ, а потому

ih

b м/ск.

Для любой точки, взятой на диаграмме (s, <)> можно провести с достаточной точностью касательную, а через точку 0 ей та параллельную линию. Соответствующая величина скорости для выбранной точки а:

где у_х=0[D= k tg ψ_χ.

Соединив вершины ординат у сплошной линией, мы получим диаграмму (», ί), причем масштаб по оси ординат в=-2- м1ск в 1 миллиметров.

^r zh ¹

Построим далее диаграмму («,s) (фигура 5), соединяя диаграммы (s, ί) и (г>, ί) при по

фигура 8, Фигура 7.

мощи вспомогательной .линии АН (фигура 6), проведенной под углом 45° к оси абсцисс; при этом масштабы пути и скоростей остаются прежними. Диаграмма (v,s) дает возможность составить представление об изменении кинетич. энергии поршенька при его подъеме и опускании. Воспользуемся известным выражением

Е =

7TV²

где ш—масса поршенька, и заменим скорость V через равную ей величину βy₁:

Е =

777 /32

-. я·

В виду того, что нам предстоит начертить диаграмму (E, s) кинетич. энергии по пути поршенька, необходимо заменить площадь квадрата у через площадь равновеликого прямоугольника az, где отрезок а следует выбрать таким образом, чтобы при у_1тах,

^гтая был равен величине, удобпой для построения диаграммы (Е, s):

Е =

τηβ²

τνβ²α 2

ζ=λζ,

где λ=(кгм в 1 миллиметров)—масштаб кинетической энергии. При помощи вычислений или простых геометрии, построений мож но найти величину ζ=~ и построить по точкам диаграмму (E, s) (фигура 7). Изменение кинетич. энергии на величину dE происходит под влиянием внешней силы Р на пути ds. В данном случае сила Р получается от сжатого воздуха, поступающего в цилиндр из подводящей трубы, соединенной с компрессором. Так как dE=P ds, то

_P=dE

ds

ИЛИ

Р =

λ dz adx

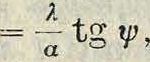
где ψ есть угол, образуемый касательной к кривой (E,s). Для графического построения ординат кривой (Р, s) проведем через точку 0₃ (фигура 8), лежащую на оси абсцисс, ряд линий, параллельных к касательным к кривой (В, s), причем построение выполним лишь для той ветви кривой (E, s), которая соответствует обратному ходу поршенька непосредственно перед ударом его о зубило. Проведенные через точку 0₃ линии отсекают на вертикали Οί, восставленной перпендикулярно к оси абсцисс, ряд отрезков: ОД, 0₃2 и т. д., пропорциональных силам Р_г, J?₂, ., так как из прямоугольного треугольника 0₃20₃имеем: 0₃2=z₃=k₁ tg у>, следовательно

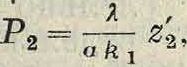
или

Р₂=δ ζ_%,

где (5=--масштаб сил диаграммы (Р, s)

(фигура 7). Отложим полученные отрезки z, z .г- оси абсцисс на соответствующих ординатах диаграммы (E, s), затем соединим вершины отрезков линией 1”2"3"4"; полученная кривая дает зависимость между силой Р, ускоряющей поршенек, и пространством, пройденным им от того момента, когда скорость поршенька равнялась нулю. Заштрихованная площадь диаграммы пропорциональна работе и имеет масштаб: 1 миллиметров² — ад кгм. Измерив площадь f в миллиметров²· и помножив на масштаб, мы получим ту работу А=fad кгм, которую поршенек мог бы отдать на перемещение режущей кромки зубила, если бы не было упругих деформаций как самого зубила, так и бойка, в который ударяется поршенек. Указанные упругие деформации, аккумулируя часть работы во время удара, отдают ее обратно бойку, отбрасывая его со скоростью г₀ м/ск, причем v₀ можно определить по диаграмме (υ, f), а потерянную кинетическую энергию по диаграмме (E, s) или непосредственно по формуле Е=^т^’. Проверкой правильности построения диаграмм (E, s) и (Р, s) служит равенство:

-л mv?, о

~ 2 ^— ’

откуда можно получить величину скорости поршенька перед самым ударом и сравнить ее с той же скоростью, но полученной из диаграммы (г, <). Если величину dE получить аналитически, диференцируя выражение кинетической эпергии Е=”^², то можно составить ур-ие:

dE=mv dv=m~dv=P ds,.

откуда х> dv.

Р ~т _dt =mj;

поэтому диаграмма (Р, s) дает также и зависимость величины ускорения j поршенька от пути, причем масштаб ускорений в

Υ

м1ск² в 1 миллиметров.

Инж. Гределем были сняты при помощи оптич. индикатора диаграммы давлений воздуха под и над поршеньком. Эти диаграммы (уменьшенные вдвое) даны на фигуре 9; масштабы: по оси ординат: 1 миллиметров—Vs кг/см² и по оси абсцисс: 1 миллиметров—0,002 м, следовательно 1 миллиметров² площади диаграммы представляет работу 4 ·1Ο^_4·Εκ0Λ, причем вэтом выра

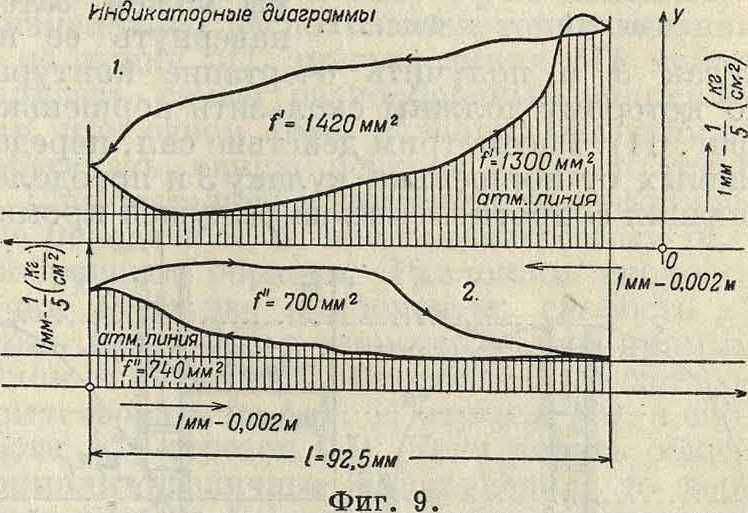
жении F — площадь поперечного сечения цилиндра в см². Измеряя площади индикаторной диаграммы в миллиметров² и помножая полученный результат на Fad, мы найдем величину работы, затраченной на получение одного удара. Величина же полученной работы м. б. вычислена по формуле:

ei та mvf-mvS

Ει-ϋ₀=-г--

Отношение полученной работы к затраченной носит название коэфициента полезного действия η. В данном случае величина η по Гределю равна 0,9.

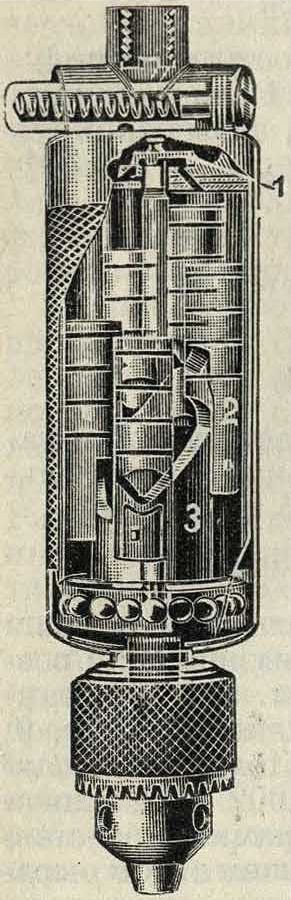
. Вторым примером будет служить сверлилка англ, системы Desoutter. В этом аппарате непрерывное вращательное движение сверла получается в результате возвратно-поступательного движения поршеньков, скользящих в каналах под действием сжатого воздуха, поступающего через гибкую трубу с торца аппарата и распределяющегося надлежащим образом по каналам благодаря вращающемуся диску 1 (фигура 10). Каждый из поршеньков при своем движении скользит своим нижним концом, отмеченным на той же фигура 10 цифрой 2, по краю кулака 3, заставляя вращаться его ось

ныл

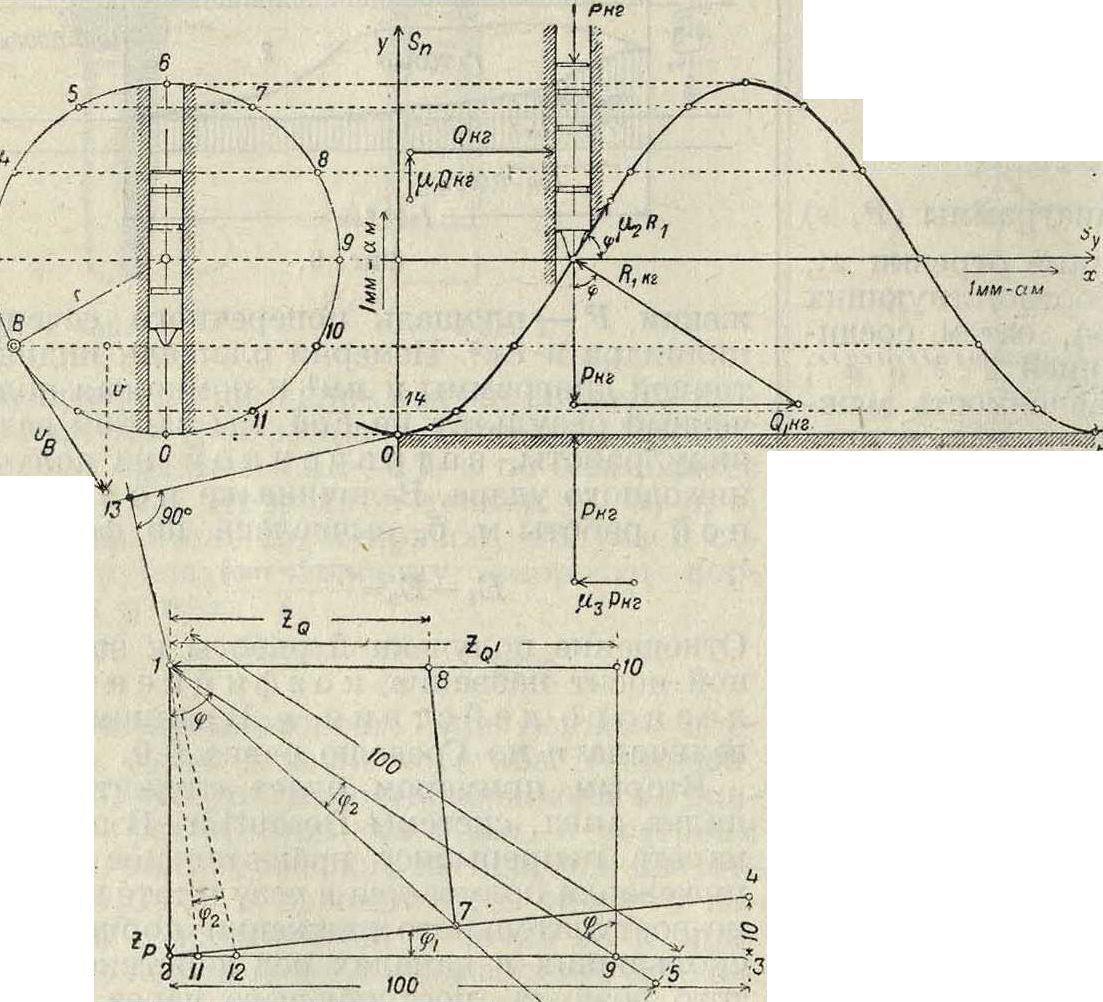
Предположим, что иа поршенек в его среднем положении давит сжатый воздух с силой Р кз (фигура 12); разложим эту силу на две компоненты: на силу Q₁ кг, действующую горизонтально, и на силу кг, действующую по нормали к поверхности соприкосновения поршенька с кулаком 3. При этом разложении силы трения пока не были приняты во внимание. Обозначим силу трения на поверхности соприкосновения поршенька с цилиндром, в к-ром он двигается, через кг, силу трения между поршеньком и наклонной поверхностью кулака — через μ₂Ρ кг, а силу трения между опорой кулака 3 и кожухом сверлилки—через μ₃Ρ кг. Коэфициенты μ₁, μ₂ и μ₃ м. б. заменены величинами: tgy_t, tg<p₂, tg?>3> где Ψ— угол трения. Выбрав подходящий маештаб сил: 1 миллиметров—δ кг, отложим на фигуре 13

— р вертикально отрезок 1,2=Ζ_Γ= -_д-мм. Проведем через точку 1 параллель нормали к косинусоиде в точке соприкосновения поршенька с нзделонной поверхностью кулака 3, а через точку 2 — параллель основной линии косинусоиды ОН и отложим на этих линиях отрезки по 100 миллиметров, а под прямым углом к этим отрезкам отложим в точке 5 отрезок 5,6 длиной в 15 миллиметров и в точке 3—отрезок 3,4 длиной в 10 дм, что будет соответствовать выбору коэфициента трения

μ_ι=tg ψχ=ОД И μ₂=tg φ₂=0,15.

Фигура 12.

Проводя линии 1,6 и 2,4, мы получим точку пересечения 7, а через эту точку проведем линию 7,8 параллельно гипотенузе 7, 8 отдельно начерченного на фигуре 14 прямоугольного тр-ка с катетами 100 миллиметров и 10 миллиметров, что соответствует коэф-ту трения /t₃=tg <р₃=--= 0,1. Отрезок 8,i=Zq дает величину горизонтальной силы реакции согласно формуле Q — 6Zq кг. Предположим, что все коэфициенты трения μ_ν μ₂ и μ₃ одновременно превратились в нуль;тогда силе реакции Q₁ соответствовал бы отрезок Ζψ, равный отрезку 1 ,Τθ, т. к. линия 9/До пошла бы в этом случае параллельно отрез-icy Ζρ. Вычислим кпд рассматриваемой передачи сил, определив работу полученную и работу затраченную. Полученная работа, отнесенная к 1 ск., м. б. представлена формулой

А_п=Qw кгм/ск,

а работа затраченная дается формулой

A_n=Pv кгм/ск,

по часовой стрелке. Предположим, что для движения поршеньков изобретатель принял гармонии. движение, и найдем профиль верхней кромки кулака 3, ис,ходя из равномерного вращения сверла. Гармонии. движение, как известно, можно получить, проектируя точку, двигающуюся равномерно по окружности, на диаметр этой окружности. На фигуре 12 представлена косинусоида, описываемая точкой, двигающейся по диам. круга гармонии. движением, причем сам круг двигается равномернопоступательно в направлении оси абсцисс. Если же при вычерчивании косинусоиды принять ее шаг, ОН, рав-окружности кулака 3, то, вырезав эту косинусоиду из бумаги,

,. мы можем затем

Фигура ίο. Фигура и. _навер_Ну_{ТЬ ее} на

.кулак 3 и получить очертание контура, по которому должны скользить поршеньки (фигура 11). Рассмотрим действие сил, передаваемых от поршенька кулаку 3 и преодолевающих сопротивление на режущей кромке еу/о г

Фигура 14.

Масштаб /мм - ёкг

Фигура 13.

сверла, а также сопротивление трения на всех поверхностях, где имеется относительное скольжение или трение качения. где гс—окружная скорость точки соприкое-новения поршенька и кулака 3, a υ—соответствующая скорость поршенька. Следовательно кпд η будет иметь вид:

η =

Qw

но

w =

и V

dt dt

ds_n

dt

a

dy dt ’

поэтому где

_ ^ZQ dx _ ^ZQ 1 ^η~ Zp dy ~ Z_p tg φ ’

tg φ —

dy dx ’

a φ есть угол наклона касательной к косинусоиде", проведенной в точке касания поршенька фасонной поверхностью кулака 3. Этот угол образуют также линии 2,9 и 1,2 на фигуре 13. Следовательно

Zq Zq Zp Zq

tgy=у--, а потому η=Д

- Ζ_ρ Z_p Z_q- Zq

Кпд в данный момент времени зависит от положения поршенька. При среднем положении поршенька получаем наибольший кпд; для других положений поршенька он будет меньше. Не трудно установить тот наибольший наклон касательной к косинусоиде, при котором кпд передачи делается равным нулю. Т. к. в этом положении Zq=О, то проведем через точку 1 линию 1,11 параллельно линии 7,8 и отложим от этой линии угол φ₂, соответствующий углу трения, заключенному между линиями 2,5 и и 1,6. Полученная линия 1,12 параллельна нормали в искомой точке косинусоиды, а проводя к линии 1,12 под прямым углом касательную к кривой 23,24, мы получим ту точку 24, в которой η=0. Следует наконец отметить, что в действительном приборе все коэфициенты трения — μ₂ и в особенности ц₃ — значительно меньше, чем были взяты нами, чтобы сделать построение многоугольника сил более понятным.

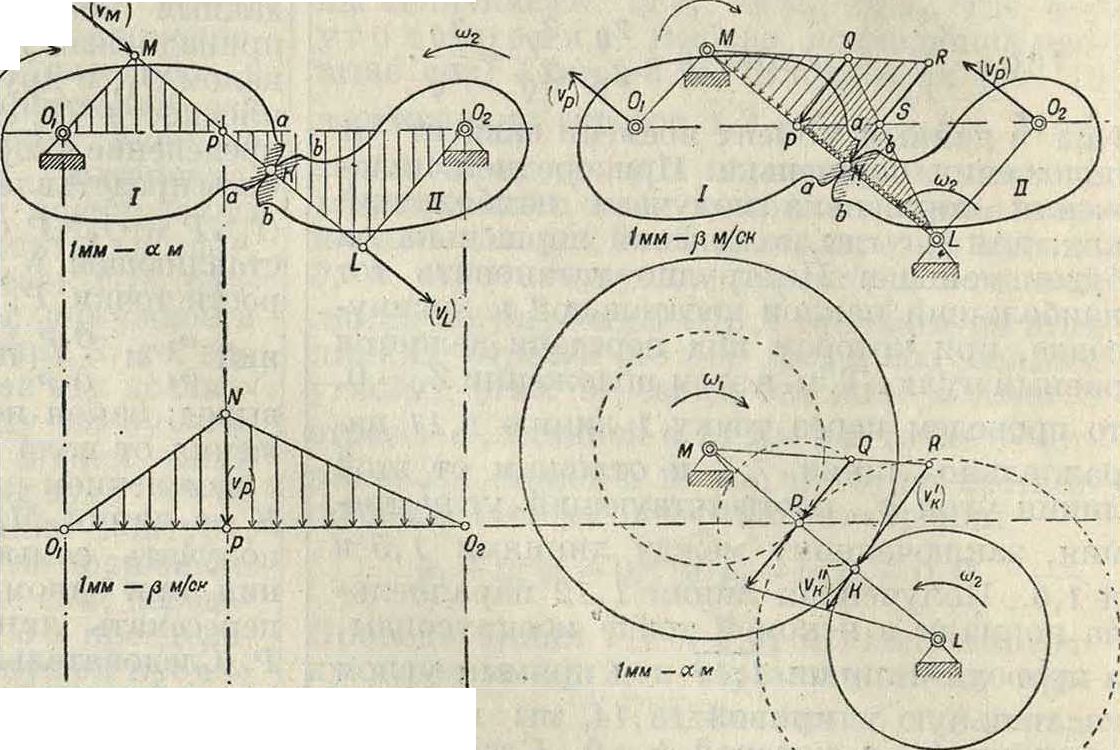
Передача вращательного движения между параллельными осями составляет одну из наиболее важных областей М. п. Ограничимся указанием на самые основные, руководящие положения и дадим соответствующие графич. построения. Предположим, что требуется передать вращение от вала О_х к параллельному с ним валу 0₂так, чтобы отношение их угловых скоростей ωχ и со₂ было равно ёаданной величине. Это отношение м. б. величиной постоянной или переменной. На фигуре 15 представлены две плоскости I и II, перпендикулярные к осям О_х и О а и вращающиеся вместе с ними. Предположим, что обе плоскости ограничены контурами аа и Ьb и касаются друг друга в точке К, причем нормали в точке соприкосновения должны совпадать друг с другом. Опустим на эту общую нормаль перпендикуляры из геометрии, центров вращения Οχ и 0г и обозначим точки пересечения этих перпендикуляров с нормалью через Ми L. Скорость точки Μ, ν^α-ΟχΜ·ω_χ, а скорость точки L, v_L=a- 0₂L ω₂, где а— масштаб чертежа. Основное условие, при котором оба контура, аа и bb, будут иметь точку касания К, состоит в том, чтобы скорости точек М и L, как лежащих на об щей нормали, были равны: v_M= v_L, или О_гМ ω₁=0₂L ω₂, откуда

to₂ __ ο χ м <°ι~ o₂l

Обозначим буквой Р точку пересечения общей нормали ML и линии О_х0₂ и, пользуясь подобием тр-ков ОД?М и 0₂РЬ, заменим в основном уравнении отношение О_гМ : 0₂L равным ему отношением О_хР : 0₂Р; тогда или со₂ Οχ Р ^ωι о1р со₂ а 0₂Ρ=ω_χ а ОД?=ν_ρ м/ск, где ν_ρ—скорость точки Р, совмещающей в данный момент как бы две точки: одну, принадлежащую плоскости I, связанной с валом Οχ, и другую точку, принадлежащую плоскости II, связанной с валом 0₂. Распределение скоростей на линии 0χ0₂ мож-т быть представлено на фигуре 16 двумя тр-ками О_хИР и 0₂ИР с общей стороной ΝΡ, представляющей в масштабе 1 миллиметров—β м/ск скорость точки Р, то есть ν_ρ. Равенство отноше ний -- и °¹ позволяет сделать Следующий “1 О_гР

вывод: закон передачи вращательного движения от вала Οχ к валу 0₂ не изменяется с изменением расположения точки касания К на линии ML, причем линия ML может получать самые разнообразные направления, при одном лишь условии: она должна пересекать линию центров 0_Х0₂ в точке Р. Следовательно конструктивное оформление передачи м. б. произведено самым разнообразным образом. Разложим скорость точки Р на две компоненты: скорость vp вдоль линии ML и скорость vp под прямым углом к линии ML. Скорости v_P будет соответствовать на фигуре 17 отрезок NQ, а скорости v"p—отрезок QP. Если давать общей нормали различные направления, то вершина вектора NQ, точка Q, будет описывать окружность диаметра, равного ИР, как это указано на фигуре17. Скорость ν_Ρ равна скорости точки М и скорости точки L:

»р=«ж=v_L,

так как эти точки лежат на одной и той же прямой, совпадающей с общей нормалью к контурам в точке соприкосновения. Дадим всем точкам нашей системы скорость равную, но противоположно направленную скорости v’p. Точки М и L делаются при этом новом движении центрами вращения плоскостей I и II, причем угловые скорости этих плоскостей остаются прежними: ω_χ и ω₂. На фигуре 18 дано построение тр-ка скоростей для линии МК и тр-ка скоростей для •линии KL. Скорость точки К, как принадлежащей контуру плоскости I, представлена отрезком RK. а скорость той же точки К как принадлежащей контуру плоскости II, представлена отрезком SK, а так как масштабы скоростей одинаковы (1 миллиметров—β м/ск), то разность этих отрезков Ϊ1Κ—8Κ =118 пропорциональна относительной скорости скольжения одного контура по другому. Уничтожить это относительное скольжение можно лишь в том случае, если поместить точку соприкосновения контуров, то есть точку К, в точку Р.

Инж. Бонди предложил изучать трение в зубчатых зацеплениях экспериментальным путем, заменяя действительные зубчатые колеса двумя дисками, представленными на фигуре lit. Радиусы этих дисков соответственно равны МК и KL, а их окружные скорости м. б. получены по ф-ле:

Vg= ω,α МК мск, ν’χ=oj₂a LK м/ск.

Эти диски могут приводиться в движение при помощи двух нормальных зубчатых колес, показанных на фигуре 19 пунктиром. Радиусы этих колес МР и PL, а окружная скорость одна и та же vj>. Если дис- ^ ки будут прижиматься друг к другу той же силой, которая передается по нормали от плоскости I к плоскости II, то изнашивание дисков будет происходить так же, как и контуров но и bb плоскостей I и II. Предположим, что с вала I на вал II передается момент Μχ кгм; если обозначить силу, передаваемую по нормали к контурам, буквою U, то можно составить следующее уравнение:

М₇=Ϊ7 · а (Щ, откуда т-г Мг

U=—= кг, a · О i М

следовательно сила трения в точке соприкосновения будет иметь величину μϋ, где μ—коэф. трения, а секундная работа трения м. б. дана ф-лой:

А=μΐΙ(ν^— νκ) кгм/ск.

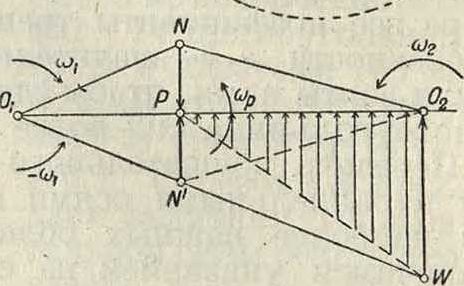
Эту формулу можно упростить, вводя угловую скорость в относительн. движении для плоскости 11 по отношению к плоскости I. Дадим всей. системе вращательное движение относительно вала О, с угловой скоростью (— ар); при этом плоскость I сделается неподвижной, а плоскость Л будет вращаться в данный момент относительно точки Р (полюса мгновенного вращения в относительном движении) с угловой скоростью ω_ρ. Пользуясь фигура 20, мы можем составить выражение скорости a-0₂W самой оси 0₂:

^ о₂ ⁼ (^{— ω}ι) ^α ’ ΟχΟ%=со_р - a Ρ0₂, откуда

А=— μ-U a РК (ω_ί -f cu₂) кгм/ск. Предыдущий анализ движения предполагал вращение параллельных валов Οι и О, в разных направлениях; если же вращение ар и ар должен быть осуществлено в одном направлении, то полюс Р выйдет за пределы линии 0,0г, а угловая скорость ω_ρ в относительном движении равна разности угловых скоростей ωχ и ар. Поэтому выражение секундной работы трения будет иметь вид: Α=—μ·ΙΙ·α· ΡΚ(ω₁ — 0)₂) кгмвК.

Эта формула показывает, что работа трения в передачах с одноименным вращением меньше (при равенстве всех других условий),

I I |ч^>	i
i ч !
-β м/сн J
|0 Р*	ίΝ. Λ

I

о,о,

со=— COi —Li.

^р РОД

следовательно о,р но ОА=Ο,Ρ + 0*Р,

Φ+i).

— ₀ μ со(, поэтому ω_ρ=- К + со_а). Скорость относительного скольжения равна a РК · ω_ρ, а потому секундная работа трения выразится так:

Фигура 15, 16, 17, 18, 19 и 20.

чем в передачах с разноименным вращением. Рассматривая вращательное движение за длительный промежуток времени, мы можем установить тот факт, что полюс Р остается в одной и той же точке на линии 0,0₂, если отношение скоростей ар и ар—величина постоянная. В этом случае геометрнч. место точек, принадлежащих плоскости I и плоскости 11, последовательно совпадающих при вращении этих плоскостей с полюсом Р, дает окружности, описанные радиусом О_гР относительно центра Οχ, и радиусом 0₂Р относительно центра 0₂. Если же отношение скоростей ар к ар меняется в зависимости от времени, то полюс Р перемещается по линии 0,0 ₂, а соответствующие геометрич. места точек плоскости I и II, совпадающих при вращении с полюсом Р, образуют сложные кривые и м. б. найдены в большинстве случаев лишь графически.

Рассмотрим случай передачи вращательного движения между параллельными осями

ΐΜΜ²—57.3τσ

при переменном отношении угловых скоростей, причем примем, что диаграмма изменения ω_ι по времени имеет вид синусоиды, .а соответствующее изменение <ю_а по времени дает диаграмму из ряда наклонных линий, как указано на фигуре 21. Расположим диаграммы (со, I) и (ω₂, ί) так, чтобы их начало координат совпадало с геометрия, центром вращения оси О,и О _г.Масштабы для диаграмм выбираем одинаковыми: 1 миллиметров—тек. по оси абсцисс и t миллиметров—σ ек.^-1 по оси ординат. Проектируя ординаты, соответствующие одному и тому же моменту у времени ί=τ,г, на оси ординат и соединяя полученные точки, мы получим на линии 0ι0₂ точку пересечения Р, т. к. из основного ур-ия мы будем иметь:

<о₁_ 0,Р

"1 ~~ ид ’

из подобия же треугольников О! W Р ,з и О aIIР₁₃получим:

о I Р13 ОIVV ОУ2 _

77^Р,з (Дн °Vi “I На фигуре 21 построены этим методом точки Р₁₃ и Р₂, при- —

чем точка Р₁₃ служит полюсом для момента времени=тг_л и для момента времени (₃=т.г₃ благодаря сим-.

метрик диаграмм (cu_u ί) и (со₂. ί). Точки плос-.костей 1 и h, совпадающие в рассматриваемый момент в точке Р₁ на линии Οβχ, находились за ί, ск. до этого момента в точках Pi и Р/. Эти точки м. б. найдены, во-первых, потому, что они лежат на дугах, описанных из О_г и О г радиусами: ОД и ОД, а во-вторых, потому, что углы, образуемые линиями OjPi и О_гР[ с линией центров 0,0₂, пропорциональны площадям /, и //, взятым над абсциссами х[ и х" на диаграммах (о»!, ί) и (cu₂, t). На основании ур-ия:

dq> ^ω ~ ~dt

можем определить величину угла, ί

φ=J ω dt,

о считая, что угол, соответствующий t=О, тоже равен нулю; в нашем случае г¹

φ[=στ Ух dx=στ/i радиан,

Положение точки Р на линии ()_{О_г при t — О в нашем случае не м. б. построено, так как при этом у_г=у_%= 0; поэтому можно применить приближенное построение, заключающееся в том, что полученные полоиды Ρ₂Ρ[άΡ"ΡΙ продолжают до пересечения с ли

1мм^г — <гг радиан

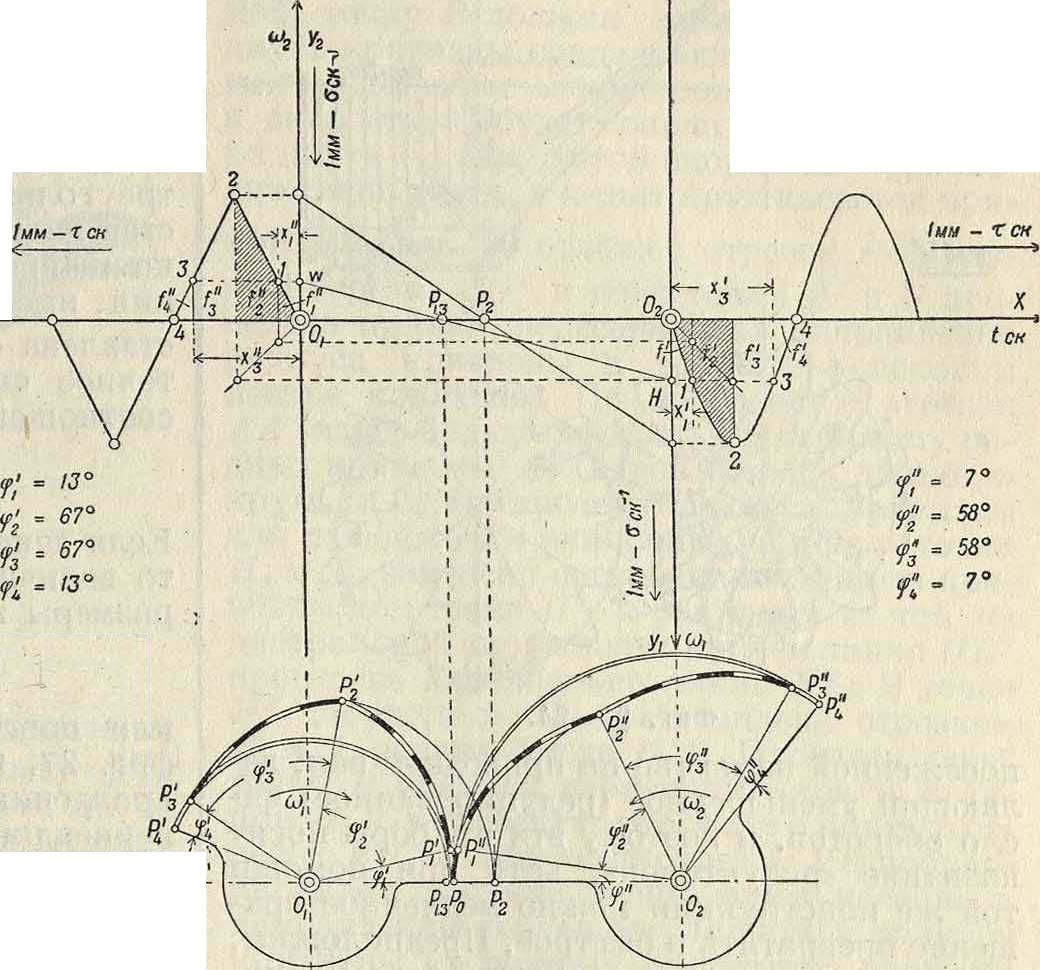
Фигура 21—22.

JL

"=στ J y₂dx=στ/"

Ψ

Вводя множитель 57,3, мы можем определить углы в градусах. Аналогично указанному определены на фигуре 22 радиусы и углы точек (Pi, Р₃) и (Pi, Р^) и построено геометрическое место полюсов Р в относительном движении. Эти кривые носят название полоид или центроид. нией О jO 2 в одной и той же точке Р₀, причем касательная, проведенная к одной полоиде в точке Р₀, должен быть касательной и к другой полоиде в той же точке. Основным свойством полоид является то обстоятельство, что движение одной полоиды по другой совершается без скольжения, а это свойство ставит требование, чтобы длина полоиды Р„Р£ была равна длине полоиды Р₀Р". Полученные полоиды в большинстве случаев не м. б. непосредственно использованы для передачи вращательного движения между параллельными осями. Чтобы создать передачу конструктивно правильной формы, необходимо снабдить полоиды зубцами так же, как это делается у обыкновенных ци-линдрич. зубчатых колес (смотрите). В нашем первом примере полоиды получились в виде двух разомкнутых кривых, совершающих колебательное движение относительно центров валов Οχ и 0₂. Второй пример, указанный на фигуре 23 и 24, дает замкнутые полоиды, приспособленные для вращения в одном и том же направлении. Па фигура 24 показаны также зубцы, профиль которых получен методом циклич. зацеплений. Зубчатые колеса этого вида носят в М. п. название «некруглые колеса».

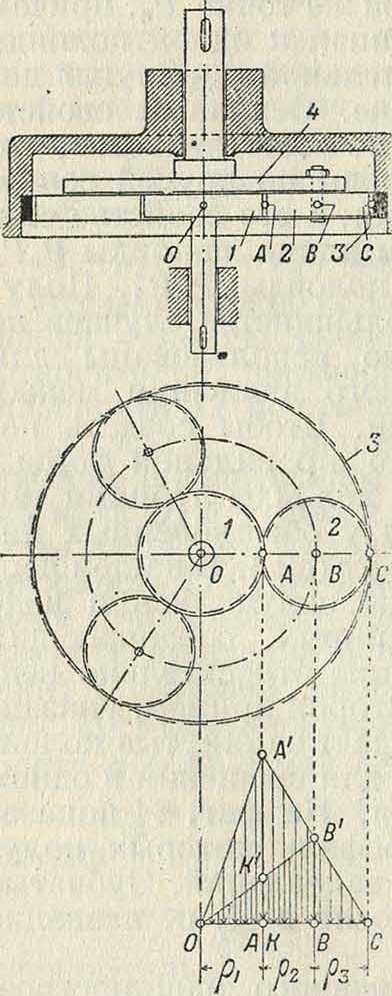
В практике современного машиностроения большое распространение получили так называемым «планетные передачи», вытесняя громоздкие ременные или обыкновенные зубчатые передачи. Схема такой «планетной передачи» простейшего типа дана на фигуре 25. Шестерня 1, соединенная намертво с валом, делающим большое число оборотов,

сцепляется с зубчатым колесом 2, а это колесо катится по зубчатому венцу 3. Ось зубчатого колеса 2 укреплена на шайбе 4,

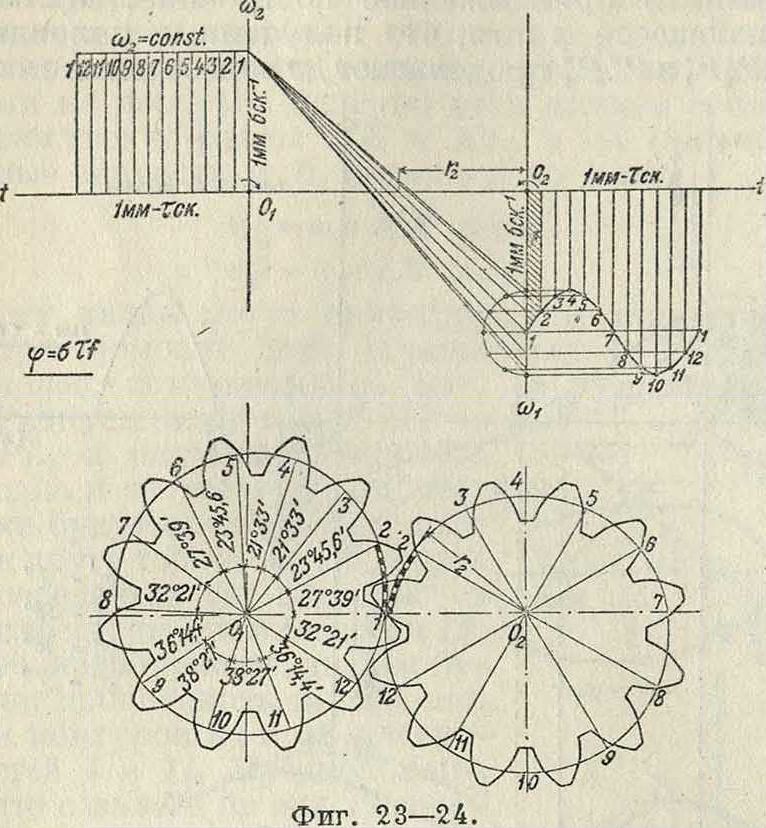
посаженной намертво на приводной вал, делающий уменьшенное (редуцированное) число оборотов, и поэтому эти приборы носят название «редукторов», хотя при помощи той же конструкции можно медленное вращение превратить в быстрое. Предположим, что угловая скорость шестерни ί нам дана, а также известны радиусы всех зубчатых колес. Обозначим точку соприкосновения первой шестерни с зубчатым колесом 2 буквой А, ось зубчатого колеса 2 буквой В, а точку соприкосновения зубчатого колеса 2 с зубчатым венцом буквой С. Скорость точки А ν_Α= ρ₁ω₁ представим на фигуре 26 отрезком./!^ миллиметров, затем соединим точку А с точками О и С. Распределение скоростей на радиусе <?, будет давать треугольник О А А, а распределение скоростей на диаметре зубчатого колеса 2 дает тр-к А А С, причем точка С скорости не имеет, являясь в данный момент полюсом мгновенного вращения _ при качении колеса

Фигура 25-26. /_внутри венца 3.

Скорость точки В пропорциональна отрезку BB, а этот отрезок равен половине отрезка АА, т. к.-точка В делит сторону АС треугольника пополам, а сам отрезок ВЬнаправлен параллельно линии АА. Поэтому

^νΛ 6⁽⁰1

^VB=2 ⁼ V ^М/СК’

но точка В соединена намертво с шайбой 4, а потому угловая скорость этой шайбы а>₂найдется из ур-ия:

νη ρ,

ω.,=—в—=со, ———г · βι+β₂ ¹2(βι +е₂)

Следовательно, передаточное число _ε _ ^2 __et__

“1 2,Cl + ρ,)

Соединим точку В с точкой О. Полученный треу голыш к OJ3Bдает распределение скоростей на радиусе шайбы 4. Точка К, взятая на шайбе на расстоянии ρ, от оси вращения, имеет скорость г_к=д,о)₂ и м. б. представлена отрезком КК, а потому передаточное число е м. б. определено также из соотношения:

^ _ ριω₂ _ V>K _ Ε Κι 6ι^ω i VA ΑΑι

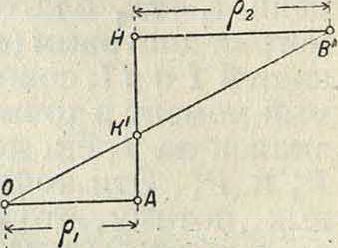
Если дано передаточное число ей радиус ρ_ΐ7то величина радиуса ρ₂, а следовательно и размеры венца, м. б. найдены по ф-ле:

Фигура 27.

или простым построением, указанным на фигуре 27. Отложим по горизонтальному направлению радиус и проведем к нему перпендикуляр через точку А; на этом перпендикуляре отложим выбранный отрезок

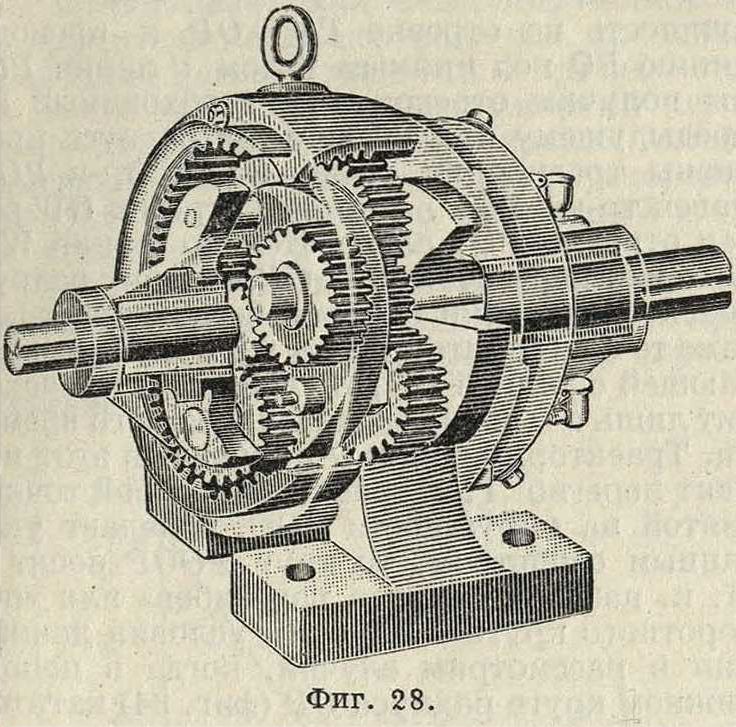
АК и вычисленную величину АН=: проводя затем через точки О и К наклонную линию, а через точку II параллель радиусу мы найдем величину ρ₂ в виде отрезка НВ. Рассмотренная система редуктора дает небольшие конструктивы. размеры только при уменьшении числа оборотов не больше, чем в восемь раз. Если требуется большое уменьшение угловой скорости, то помещают один редуктор за другим (в одном кожухе), причем дают в одном редукторе уменьшение в четыре раза, в другом редукторе в пять раз. В результате работы сдвоенного редуктора мы получим уменьшение скорости в 20 раз. Общий вид двойного редуктора системы Гень-шау дан на фигуре 28.

Перейдем теперь к рассмотрению траекторий, описываемых различными точками какой-нибудь системы, и к определению их радиусов кривизны. Для разрешения этой задачи мы будем пользоваться, как основным приемом исследования, методом проф. Гартмана, применяемым с успехом в тех случаях, когда полюс мгновенного вращения легко получить в пределах чертежа; во всех других случаях решение можно найти методом нормальных ускорений. Рассмотрим наиболее простой случай: круг катится без скольжения по прямой линии; требуется определить траекторию одной из точек окружности и построить для различных точек, взятых в плоскости круга, радиусы кривизны траекторий этих точек. Возьмем круг некоторого определенного дио метра АР=d миллиметров и развернем его окружность, равную r.d миллиметров, в прямую линию KL (фигура 29). Разделим эту длину на 24 равные части и перенесем эти деления взят равным ВВ. Проведем линию АВ и продолжим ее до пересечения с линией АВ. Точка пересечения, отмеченная буквой С, даст искомый центр кривизны. В рас

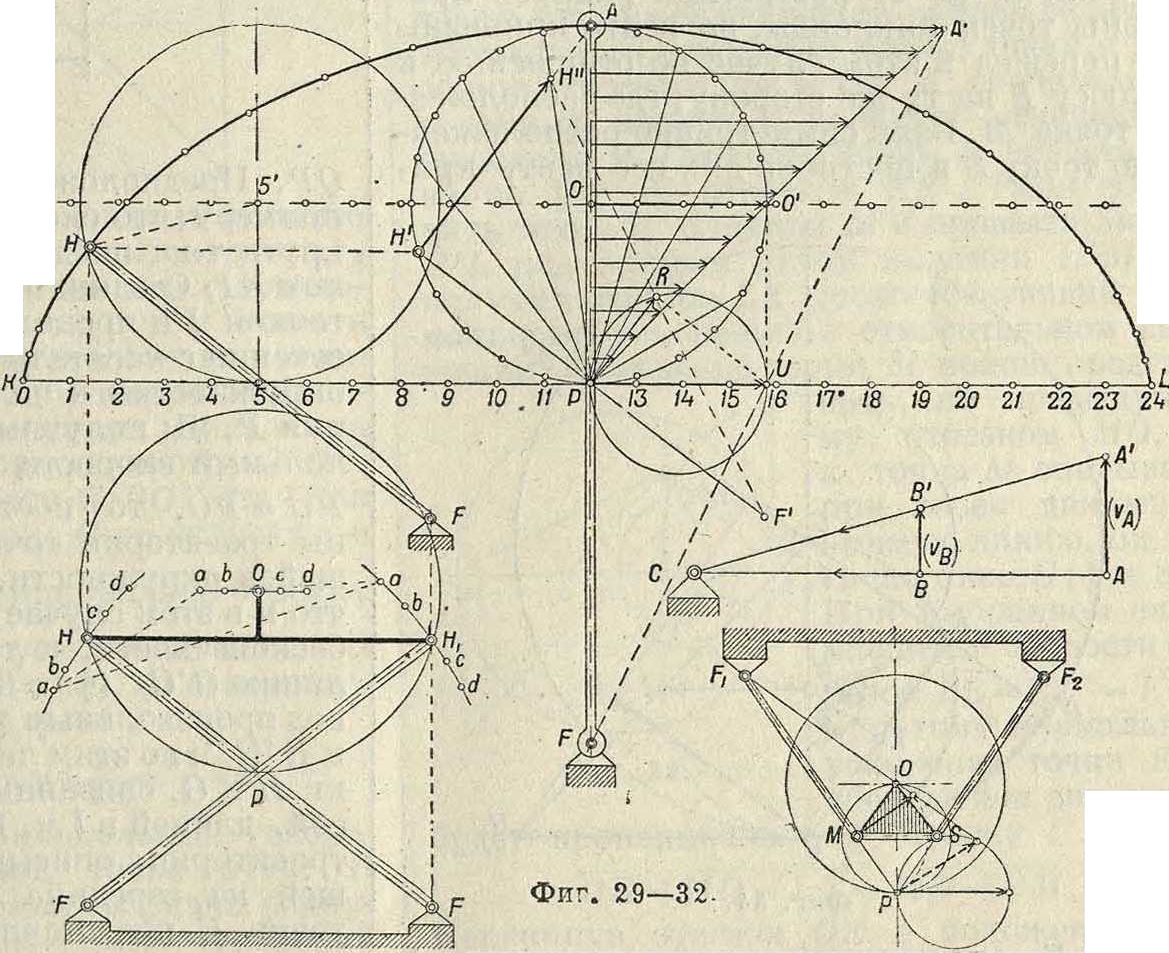
сматриваемом нами движении круга по прямой точку В должна заменить точка радиуса кривизны, совпадающая в данный момент с полюсом мгновенного вращения Р, а скорость v_B будет равна скорости центра круга г₀, т. к. с этой скоростью происходит смена точек, в которых круг касается пря на прямую линию NN_U проведенную через центр круга О параллельно линии KL. Разделим также окружность круга на 24 равные части и проведем к точкам деления хорды из точки касания Р Круга с прямой KL. Кривая, описываемая точкой А, взятой на окружности, называется циклоидой и м. б. построена по точкам, получаемым при помощи засечек, например точка циклоиды В получается засечкой радиусом 4i5 из точки S и засечкой отрезком ыЩ равным хорде ВР. Найдем центр кривизны циклоиды для положения точки А на вертикальном диаметре АР. Предположим, что круг катится по прямой KL со скоростью ν₀ м/ск. Представим на фигуре 29 эту скорость центра круга отрезком 00, равным ^N радиусу круга; следовательно распределение скоростей на вертикальном диаметре АР можно дать тр-ком скоростей РАА, проводя линию РА через точку О. Определение центра кривизны (точка F) сводится, по мысли проф.

Гартмана, к построению треугольника скоростей для радиуса кривизны FA по двум отрезкам: первый отрезок соответствует скорости точки А и принят на фигура 30 равным АА_b а второй отрезок соответствует (в том же масштабе) скорости другой точки того же радиуса кривизны. На фигуре 30 второй точкой выбрана точка В и соответствующий отрезок мой. На фигуре 29 отложен отрезок PU, равный отрезку 00, и через точки А я U проведена прямая, пересекающая направление радиуса кривизны в точке F — искомом центре кривизны. По построению отрезок AA’ вдвое больше отрезка PU, а потому радиус кривизны AF вдвое больше диаметра круга АР. Построение радиуса кривизны для любой точки циклоиды, например для точки M, м. б. заменено построением радиуса кривизны для точки II, которая взята на той же центральной окружности, причем линия IIII проведена параллельно линии KL. В точке Н скорость м. б. представлена отрезком IIII", равным хорде IIР. Проведем через точку Р прямую, перпендикулярную к линии И Р, и спроектируем на эту прямую отрезок PU. Полученный отрезок PR пропорционален скорости смены точек касания в направлении перпендикулярном к радиусу кривизны, а поэтому достаточно провести прямую через точки II" и R, чтобы на пересечении этой прямой с продолжением линии IIР получить центр кривизны—точку F. Тр-к PBU подобен тр-ку PHА и вдвое его меньше, а потому И И"=Ы Р =2 PH, следовательно, радиус кривизны НИ” —

-ο-Νί

Фигура 29

= 2 НР. Это равенство выражает известное из математики положение, что радиус кривизны циклоиды равен удвоенной нормали. Этим свойством циклоиды можно воспользоваться, чтобы создать целый ряд новых механизмов, обладающих той особенностью, что одна из точек этих механизмов

при его движении описывает на значительном протяжении почти прямую линию.

На фигуре 31 мы имеем механизм, состоящий из двух равных стержней, связанных шарнирно с опорой и друг с другом при по мощи траверсы. Точка О этой траверсы занимает последовательно положения а, Ь, с и d, соответствующие перемещениям точек И и Нi· Расположение этой точки О соответствует центру круга., проведенного через точки Р, Н и Н Из чертежа видно, что траектория, описываемая точкой О, почти прямая линия. На фигуре 32 дано построение радиуса кривизны траектории точки М внутри круга, описанного на радиусе ОР как на диаметре. Построение но идее ничем не отличается от построения радиуса кривизны точек циклоиды, но центр кривизны Fi перешел в этом случае по отношению к полюсу Р на ту же сторону, где расположена точка М. Взяв симметрично расположенную точку S и построив для нее центр кри

визны Р₂, мы получим механизм, известный в М. п. под названием «механизм Роберта».

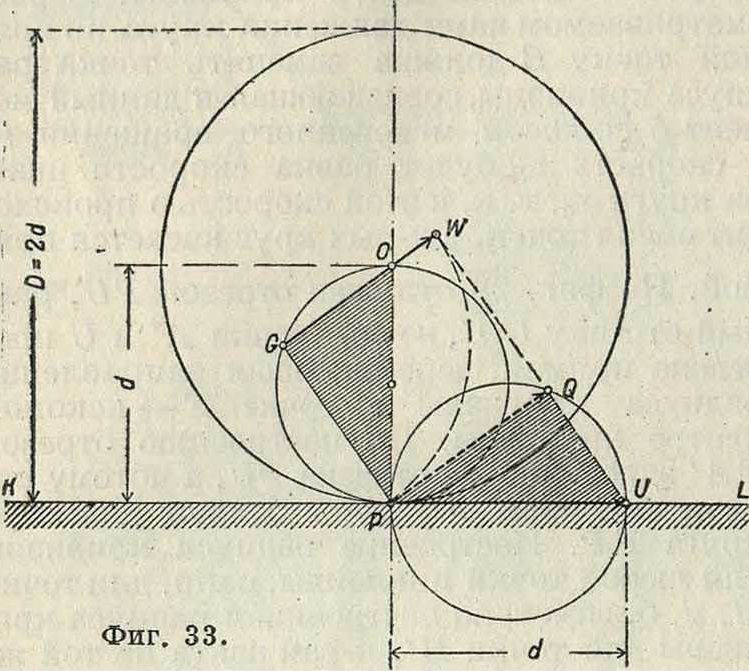
На фигуре 33 дано построение радиуса кривизны траектории точки в, взятой на окруж ности PGO, проходящей через полюс Р и центр О катящегося круга. Скорость точки

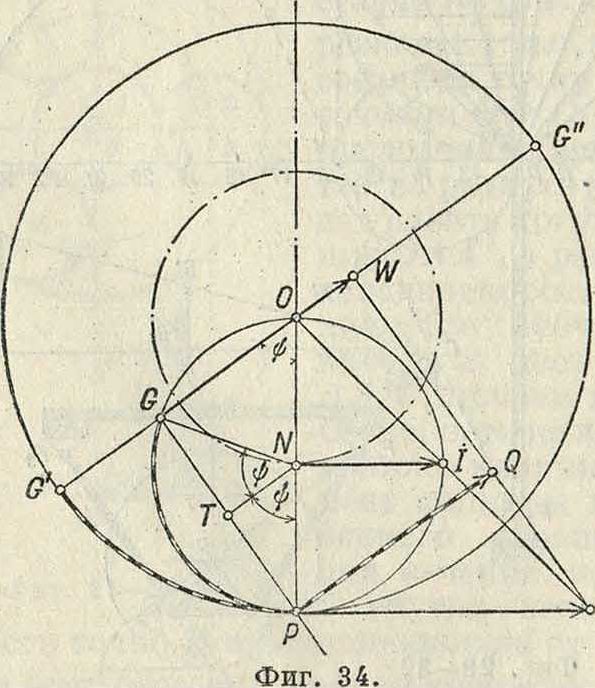
G, в масштабе β=- ^ν<>, представлена отрезов ком GW равным отрезку GP. Построив окружность на отрезке PU=UP и проводя линию PQ под прямым углом к линии PG, мы получим отрезок PQ, необходимый по предыдущему для построения радиуса кривизны траектории точки G. По тр-к PGO равен тр-ку PQU, а потому отрезок GW равен отрезку PQ; следовательно линия WQ не может пересечьлиниюСР,апотому радиус траектории точки G равен бесконечности, а сама точка G двигается по прямой, совпадающей с линией GO; это движение происходит лишь в течение бесконечно малого времени. Траектория точки G получает в этот момент перегиб. Т. к. траектория любой точки, взятой на окружности PGO, обладает указанным свойством, то круг PGOP носит в М. и. название «круга перегибов» или «поворотного круга». Изменим условия движения и рассмотрим случай, когда в неподвижном круге радиуса ОР (фигура 34) катится без скольжения круг с диаметром равным

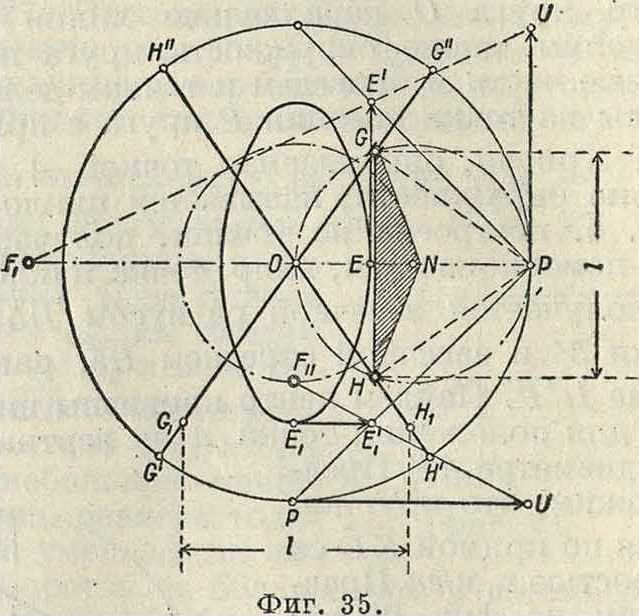
ОР. Предположим, согласно предыдущему примеру, что скорость центра N катящегося круга т-ка представлена на чертеже отрезком N1. Соединив центр О большого круга с точкой I и продолжив эту прямую до пересечения с касательной, проведенной к обеим окружностям в полюсе мгновенного вращения Р, мы получим отрезок PU, пропорциональный скорости смены полюсов. Так как PU=РО, то построение радиуса кривизны траектории точки G, лежащей на катящейся окружности, приводит нас к выводу, что и в этом случае центр кривизны лежит в бесконечности, а точка описывает прямую линию GG" (фигура 34). На фигуре 35 проведены под произвольным углом два диаметра G’G" и И П" по этим линиям двигаются ползуш-ки Н и G, связанные друг с другом траверсой, длиной в 1м. Найдем радиус кривизны траектории, описываемой точкой Е, лежащей на середине траверсы HG. Скорость точки Е представлена отрезком ЕЕ, равным расстоянию точки Е до полюса мгновенного вращения Р. Проводялинию UE до пересечения с линией РЕ, мы получим в точке Fi искомый центр кривизны. Тем же приемом определен на фигуре 35 центр кривизны Fu для расположения траверсы GJ1₁₍причем точка Е заняла положение Е_х на вертикальном диаметре. Путь точки Е при качении малого круга внутри большого будет представлен, как известно, эллипсом, и определенные выше радиусы кривизны позволяют легко установить очертания этого эллипса. Только что изложенный метод прпф. Гартмана не требовал знания закона изменения скоростей, а потому ускорение движущихся точек могло быть какой угодно величины.

При определении радиуса кривизны методом нормальных ускорений наиболее простые результаты получаются в том случае,

когда основное движение в системе принято как равномерное движение. Так, скорость v_Nцентра круга N, катящегося без скольжения внутри другого круга, будем считать постоянной величиной, следовательно угловая скорость относительно центра Р мгновенного вращения ш/>= Const. Диаграмма скоростидочки вСфигура 34) по диаметру G G", имеет вид полуокружности G’PG", так как в любом положении точки G ее скорость, в масштабе β=^β, пропорциональна отрезку

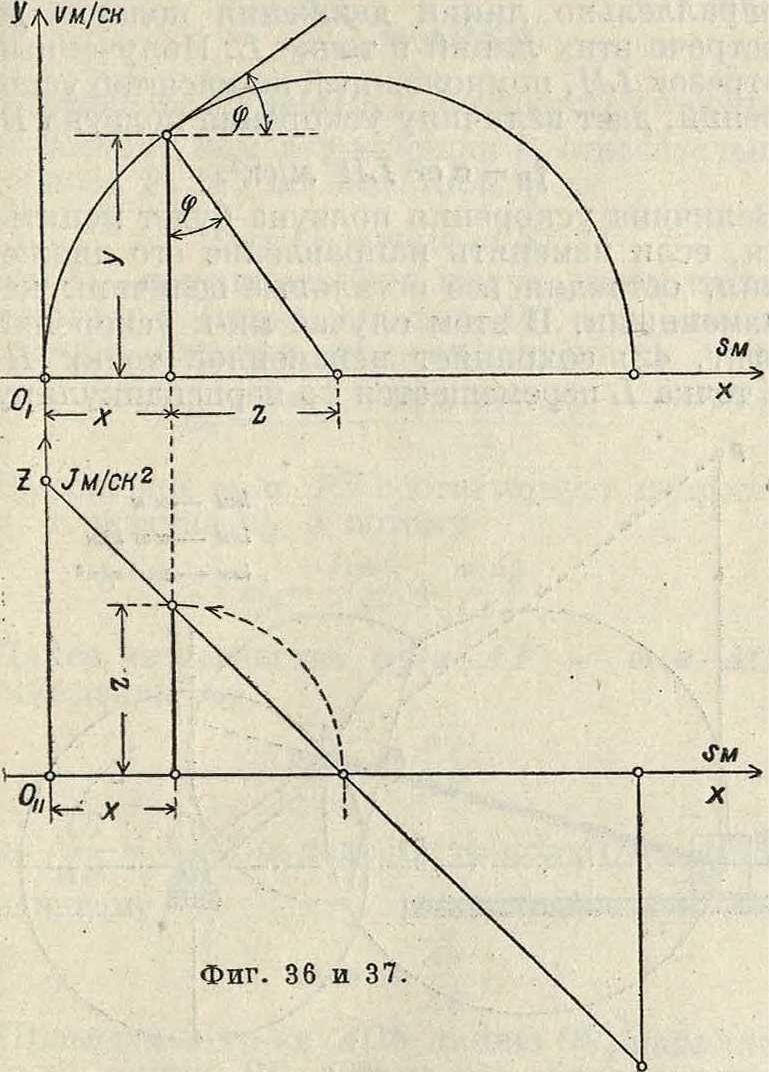
PG=GW. Диаграмма ускорений точки G найдется по диаграмме (t>„, s), на основании построения (ф ΐΓ. 36) по ф-ле

dv

dv

- тонн.

ds

y-f_x

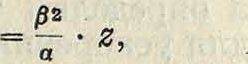
где z—отрезок, пропорциональный ускорению в рассматриваемой точке пути. В мертвых точках субнормаль z равна радиусу круга, а потому диаграмма ускорений точки G по пути s представляет прямую линию, наклоненную к оси абсцисс под углом 45° (фигура 36 и37). Зависимость нормального ускорения j" точки А в криволинейном движении от радиуса кривизны ρ траектории этой точки и ее скорости ν_Λ дается, как известно, ф-лой.

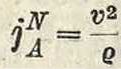
Применим эту формулу к движению по эллипсу точки Е (фигура 35). Если масштаб чертежа а м в 1 миллиметров, а масштаб скоростей, по предыдущему, принят β м/ск в 1 миллиметров, то

ir₌^.. ^,jv

* jE a F Ы ^a E *

Построение отрезка дано на фигуре 33, где тр-к EFyE взят равным такому же тр-ку на фигуре 35. Проведем линию ЕЕ" под прямым углом к линии EFi и точку пересечения линии ЕЕ" с продолжением линии EFi обозначим буквою E". Т. к.

ЕЁ"=~, то ЕЕ"=Zg.

FiE

Следовательно, зная величину нормального ускорения j_E и представив это ускорение в масштабе у=— м/ск² в 1 миллиметров отрезком ЕЕ",

мы можем получить радиус кривизны траектории точки Е, если отложим под прямым углом к направлению нормального ускорения Е"Е отрезок ЕЕ, дающий в масштабе β м/с к в 1 миллиметров скорость точки Е. Соединив точки Е" и Е и проводя перпендикуляр к ли- фигура 38.

нии ЕЕ" до пересечения в точке Fi нормали к траектории точки Е, получим радиус кривизны этой траектории в масштабе 1 миллиметров—а м. Для определения нормального ускорения точки Е в абсолютном движении найдем величину нормального ускорения той же точки в движении относительно точки М, совпадающей в данный момент с полюсом мгновенного вращения Р. Скорость точки Е представлена на фигуре 39 отрезком ЕЕ. Если соединить точку Е с точкой М и провести линию EL под прямым углом к линии ЕМ, то получим отрезок LE, соответствующий нормальному ускорению в относительном движении. Ускорение точки М можно представить, по предыдущему, отрезком МО, т. к. точка М описывает при своем движении прямую линию,аналогично точке G (фигура34). При выбранном нами масштабе скорости отрезок LE=EE=ЕМ, а потому нормальное ускорение точки Е в абсолютном движении будет пропорционально отрезку

Ш=МО-LE ^ МО - ЕМ. Перекинув отрезок ОЕ в положение EL_X(фигура 39) и соединив точки Е_г и Е, мы получим радиус кривизны точки Е, проводя ЕЕ_г под прямым углом к линии ΕΈχ.

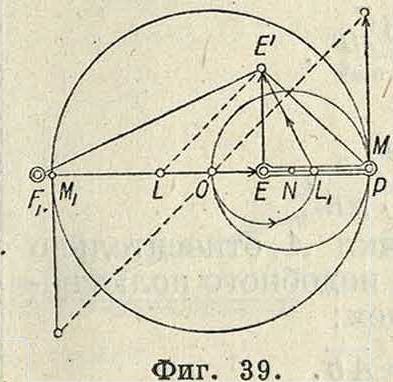
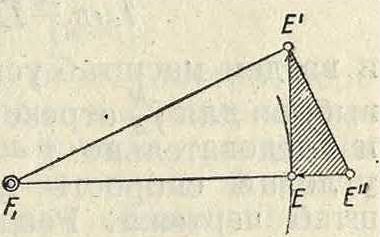
Указанный только что метод нахождения нормального ускорения точки Е в абсолютном движении есть частный случай теоремы Эйлера, выражаемой следующим геометрическим равенством:

П^Гв~+*]_ш.

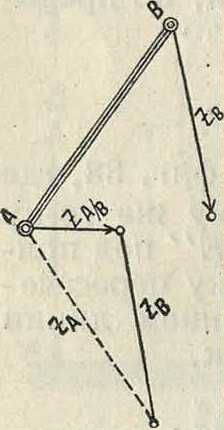
На фигуре 40 введены следующие обозначения: вектор Z_B представляет полное ускорение точки В в абсолютном движении; вектор Z_AlB представляет полное ускорение точки А в движении относительно точки В вектор Z_Aпредставляет полное ускорение точки А в абсолютном движении. По теореме Эйлера три вектора Z_B, Ζ_Α/Β и Z_Aвсегда образуют замкнутый треугольник.

Применим эту теорему для нахождения ускорения ползуна в кривошипном механизме (фигура 41). Разложим полное ускорение j_A и j_AIB на компоненты, соответствующие нормальным и тангенциальным ускорениям:

П~-

Фигура 40.

•i^NA^i^TA

Ίαιβ

- Ϊαιβ "

Jj/B

и введем масштаб ускорений γ м/ск² в 1 миллиметров, выбрав для j_A отрезок А О; но j_A=а АО ω², и следовательно γ=αω², где ω — заданная угловая скорость кривошипа, а а—масштаб чертежа. Разделив почленно ур-ие Эйлера на полученный масштаб ускорений, получим:

Ζд =*Ζ_Β- -*Ζ_Λ!_Β,

ΖαΑ-»Ζ^τλ~-

Ζ_Β Ч-> Ζ_ΑΙΒ —И· Ζ_Αιβ

Предположим, что угловое ускорение кривошипа тоже дано, поэтому вектор

deo

dt

₇Т _ _ А “А αω²

м. б. вычислен по ф-ле

Ζ^Τα=ΑΟ%

dt ω²

ММ.

Величина Z_A/B найдется по ф-ле

,-лг

„ж _ J_A/_B

*А1В~ цщ2

7^Λ =

> ПК

“ΑΙΒ :· АВ

где ,v_Ai_B — скорость точки А относительно точки В. Из тр-ка АОЬ, подобного полюсному тр-ку АР В, мы найдем:

>=Ηίθ1ίΐ.

В этом ур-ии множитель αω представляет масштаб скорости. Следовательно

ZIV АЬ‘

^л,в==ш

мм. и засекая радиусом АВ на этой окружности хорду. Проекция АК хорды на диаметр даст искомый отрезок. На фигуре 42 дано построение мн-ка ускорений: от точки А отложен вектор Ζ_Α, равный и параллельный радиусу кривошипа АО, а перпендикулярно к к нему отложен вектор Ζ_Α, равный отрезку ОН, причем

ОН=АО — ^d“! миллиметров.

СО² dt

Далее через точку А проведена линия параллельная шатуну и на ней отложен отрезок АК, равный Ζ_Αι_в. Остается провести две прямых линии: 1) через точку К под прямым углом к шатуну и 2) через точку Н параллельно линии движения ползуна до встречи этих линий в точке L. Полученный отрезок LH, помноженный на масштаб ускорений, дает величину ускорения ползуна В:

j_B=а со² LH м/ск².

Величина ускорения ползуна будет меняться, если изменять направление его движения, оставляя все остальные величины неизменными. В этом случае мн-к ускорений (фигура 42) сохраняет неизменной точку Н, а точка L перемещается по перпендикуляру

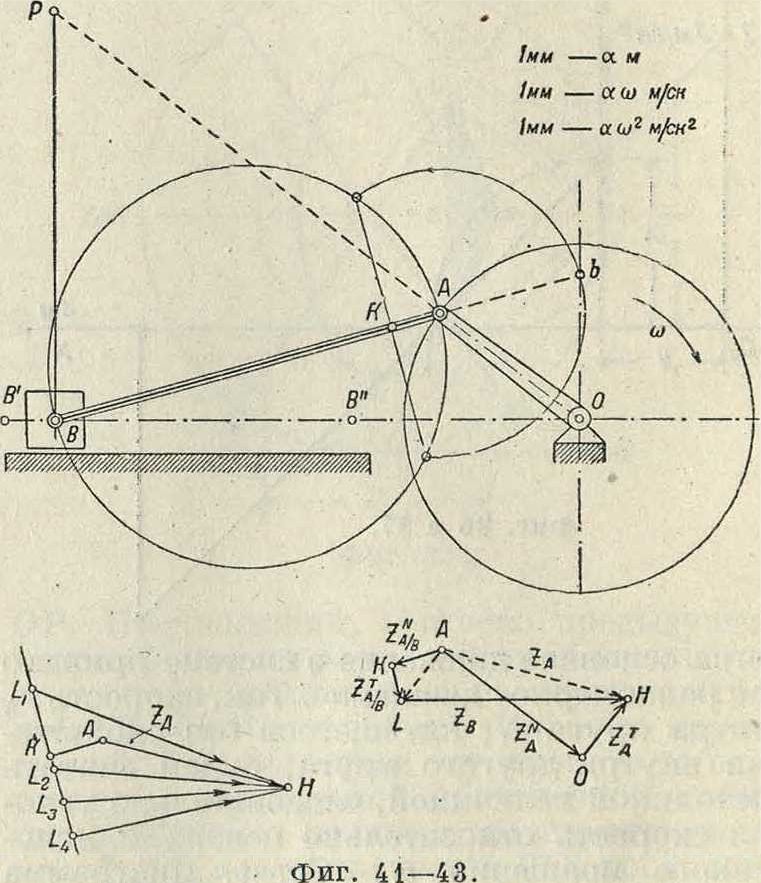
к шатуну, в зависимости от наклона линии LH, как показано на фигуре 43. Линия мертвых точек у таких кривошипных механизмов не проходит через геометрич. ось вращения коренного вала.

Рассмотрим теперь влияние масс в движущейся системе кривошипного механизма и определим ту работу, которая требуется для ускорения или замедления поступательно двигающихся частей и шатуна. Обозначим вес поршня, штока и ползуна—через G_xи вычислим массу всех реверсивно двигающихся частей

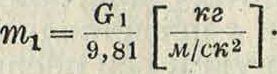
Кинетич. энергия массыпг₁ найдется по ф-ле:

Ει

m,vjj 2

Но Όρ^β-Ob, где β — масштаб скоростей, °,

равный - =, следовательно

ОА

Ел =

^ΑνΛ ( оь ²

2 1 ОА ’

Найдем кинетическую энергию шатуна Е₂, выделив элементарную ма^су т (точка К на фигуре 44) и составив для нее выражение ки-

J· π

-а. Для всего шагуна имеем:

нетич. энергии -

Σπι(αΡΚ)2 ₂-2-=

= ~ ^т(аРК)

Выражение 2 т(аРК)^г соответствует динамическому мом знлу инерции 1_Р относительно полюса Р. Но по известной ф-ле

Ip=Is Н~ ^т2 (^а PS)

где I_s—момент инерции шатуна относительно его ц. т. (точка S на фигуре 44), а то_а—масса шатуна, кинетич. энергия шатуна

τη, mola-PSyWp

= — + ——а---

Выражение ω_Ρ а PS соответствует скорости ц. т. шатуна v_s, а потому

Ei - + — ·

Далее из равенства ω_Ρ(α HP)=ω (α · НО) определим ω_Ρ:

АО

(Op — ω

АР

АО

АЬ

но -----=- _. (из подобия тр-ков АОb и АР В)

АР АВ

и питому

СОр= со

АЬ

АВ

Проведем в тр-ке Λ О 6 линию 0S₂ параллельно линии SP. Точка S₂ делит отрезок ведена параллельно линии мертвых точек, а линия S_LS₂—параллельно отрезку Оb.

VA

Отрезок 05₂ в масштабе β= -= мск в 1 миллиметров ил представляет скорость ц. т. шатуна, а потому выражение для кинетич. энергии Е₂ будет иметь вид:

Е₂ =

IgCO² 2

А Ь

лв

+

Заменив в этом выражении величину угловой скорости ω равновеликим выражением о А

ω=—= и вводя в формулу длину L шатуна а · О А

в м, получим:

Аb у,. ( 0S7 ³ ОА V ОА

Общая кинетич. энергия всего шатунного механизма, за исключением маховика и кривошипа с валом, выражается так:

Е,=

оь ² m_t ( —

V О А

is( аь V

то.

os

ОА,

Величина, стоящая в скобках, имеет размерность массы и м. б. обозначена буквой Ш:

Е=^Ю 1°^А- [кгм].

По предлоясению проф. Виттенбауера, переменная величина ЭДР носит название «приведенная масса», причем точкой приведения выбрана в нашем случае точка А—центр цапфы кривошипа. Введем обозначение:

= Ш,=т₂^3-

^{1 ί} П Л» ’ ‘ L* _ΙΙΛΖ ’ ° — о А²

ОА²

и заменим площади квадратов 0Ь^г, А Ь* и OSj площадями прямоугольников: 2/1 · ОА, У* О А, Уз-О А.

V=!S.-L._V cm, ™^{2 с}2 7.2 ГГТ #2>

«i-е·»-

Уз-

Ь² ОА "^а ОА

На фигуре 45 даны три квадрата, площади которых пропорциональны приведенным массам шатунного механизма для определенного положения кривошипа О А но отношению к линии мертвых точек, а на фигуре 46, 47 и 48 указан простой графический прием определения величин: у_г, у₂ я у₃. Построим диа-

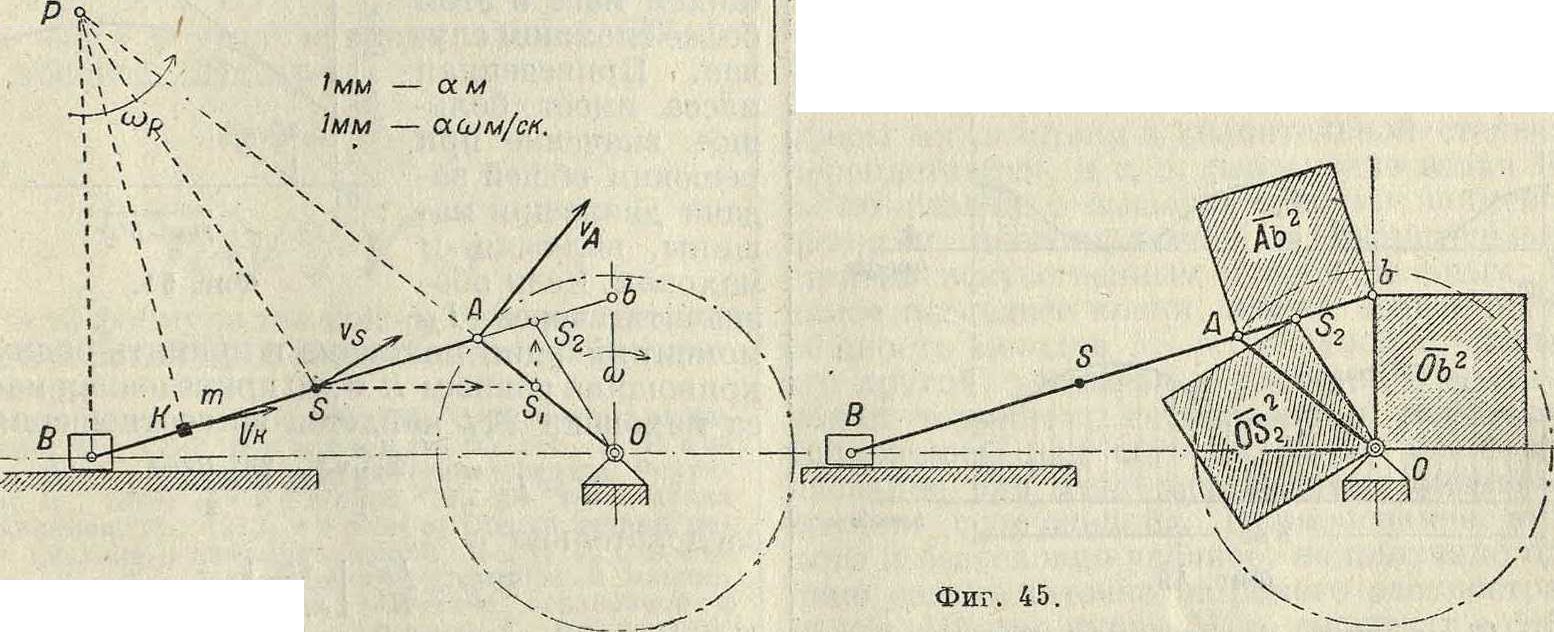
Фигура 44.

АЬ в том же отношении, в каком ц. т. делит шатун АВ. Так как полюсом Р пользоваться в кривошипном механизме невозможно, то остается получить точку S_a построением, указанным на фигуре 44, где линия SS_г про граммы приведенных масс W₂ и Sflj по пути цапфы кривошипа, выбрав для основания диаграммы отрезок h в 120 миллиметров или в 240 миллиметров. Разделив окружность на 24 части и построив для первых 12 делений соответ-

2

ствуюшие положения шатунного механизма, мы найдем отрезки Ob, АЬ и OS₂, а гю этим отрезкам построим или вычислим ор

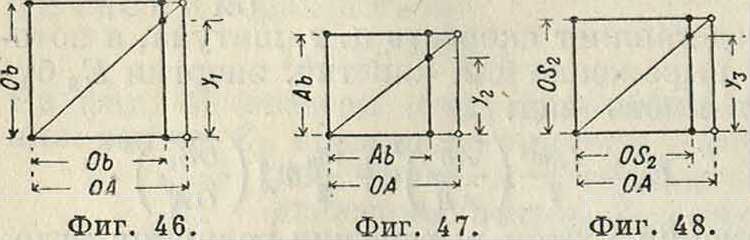
динаты диаграмм у_и у_г и у₃. На фигуре 49 даны диаграммы (2Й(, s^l, (®Ц, s_A) и Ш3. s_A); масштабы этих кривых по оси ординат соответственно равны т, ία 1 т₂

W’ я^гш- ?*-Ж

а по оси абсцисс масштаб для всех кривых будет один и тот же: 1 миллиметров—а м, причем

, 2π · а · АО

^а h ’

где h—основание диаграммы в миллиметров. Зная величину приведенной массы Ж для любого положения кривошипа, можно получить величину кинетической энергии Е, если будем располагать знанием скорости цапфы кривошипа ν_Λ. В простейшем случае ν_Α=Const, следовательно диаграммой кинетич. энергии может служить диаграмма (ШГ, s^), вычерченная в масштабе:

1

£7 =

мм—q [кг м“¹ ск²]

v*_Aq

λ · ζ

D “ (J

где λ=--масштаб кинетич. энергии.

Изменение кинетич. энергии на величину dE происходит благодаря работе внешней

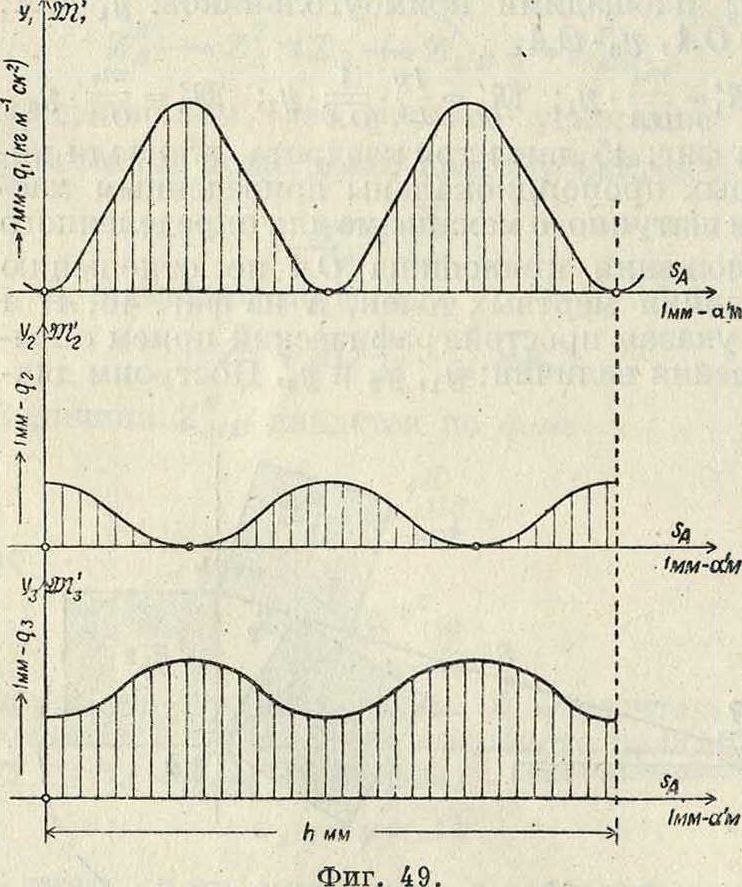
силы Т на пути ds_A, причем направление силы Т совпадает с касательной к кругу, описываемому цапфой кривошипа. Из ур-ия Т ds_A=dE имеем:

Т

_. dE ’ ds_A

λ dz a dx

λ

a

•tgy,

где φ—угол, образуемый касательной к кривой (Е, Sj(). В более сложном случае скорость v_A будет переменной величиной, зависящей от пройденного пути s^. Предположим, что диаграмма (v_A, s^,) нам дана (фигура 50), причем ординаты этой диаграммы представляют скорость v_A в масштабе β_ιΜ/βκ—1 миллиметров. Выражение для кинетич.энер гии Е =

имеет в этом случае такой вид:.

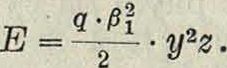
Заменим площадь квадрата у² площадью· равновеликого прямоугольника аг, а пло-

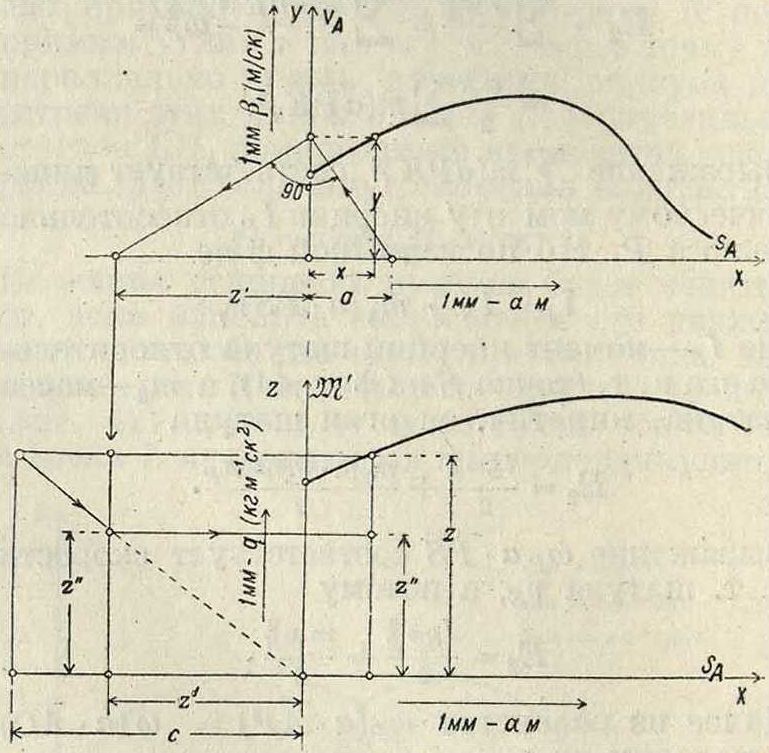
Фигура 50.

щадь прямоугольника гг—площадью равновеликого прямоугольника—сг". При этой

q · /3?ac

замене Е=- — - — · ζ. На фигуре 50 дано построение ординаты г". Проводя в точке N диаграммы (E, s_A) (фигура 51) касательную, мы можем по углу φ определить согласно предыдущему силу Т, необходимую для ускорения движущихся масс в этом более сложном случае. Приведенная масса имеет большое значение при. решении обшей задачи движения машины, включая и маховик. Если обозначить через Iи момент инерции маховика и принять радиус кривошипа равным Км, то приведенная масса маховика найдется из соотношения:

тл г “’² ®»^Д2ш2

Е=±М 2 - ~Т~ ⁼ 2 ’

следовательно

Ш-

На фигуре 52 масштаб приведенных масс— принят 1 миллиметров—q [кг л»^-1 ск“], а потому для приведенной массы маховика мы получим ординату

Y=»1.

в

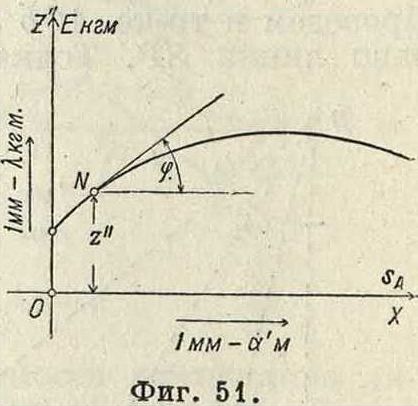
Предположим, что диаграмма кинетич. энергии (£’, Sjj) нам известна по работе сил движущих и сил сопротивления. На фигуре 52 эта диаграмма представлена в масштабе 1 миллиметров—λ кгм по оси ординат и 1 миллиметров—а м по оси абсцисс. Вычертим новую диаграмму, т.н. диаграмму Виттенбауера, приняв для нее за абсциссы величины Υ + у, а за ординаты величины г. Полученные точки W этой диаграммы лежат на замкнутой кривой, если рассматриваемое движение периодическое, в противном случае диаграмма получается разомкнутая. Из общего ур-ия

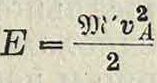
имеем:

2 _ 2Е _ гА г

^Va ~ а» ~ J ΫΤί) ‘

Соединим одну из точек кривой Виттенбауера с началом координат О и обозна чим через ψ угол наклона линии OW к оси абсцисс. Так как

^{tg ψ} “ r+y’ то

. ν_Λ=]/^Γ^ · ]/tgy>.

По этой формуле мы можем определить скорость в различных положениях цапфы кривошипа.

Лит.: Мерцало» Н. И., Кинематика механизмов, М-, 1916; Р у ж е н ц е в С. К. и Иванов Б. А., Зубчатая и червячная передача. Редуктора, М., 1930; Левепсон Л. Б., Кинематика механизмов, М., 1923; его же, Общая теория машин. Статика и динамика машин. II., 1923; Смирнов Л. П., Кинематика механизмов и машин, М.—Л., 1927; его же, Кинетика механизмов и машин, М.—Л., 1926; R e u 1 e а х F., Lehrbueh d. Kinematik, В. 1 u. 2, Brsohw., 1875—1900; Gras-h о f F., Theoretische MascUinenlelire, B. 2, Hamburg— Lpz. 1883; В urines ter L., Lehrbueh d. Kinematik, Lpz., 1886—88; Wittenbajuer F., Gra-phische Dynamik, B., 1923; Hartmann W., Die Maschinengetriebe, Stg., 1913; Tolle M., Die Rege-lung d. Kraftmaschinen, 3 Aufl., B., 1921; Prop·

ger F., Die Getriebekinematik als Riist7.eug der Getrirbedynamik, «Forscliungsarbeiten», Berlin, 1926, Heft 285; G r 0 b 1 er M. Lehrbueh d. teebnisehen Meelianik, В. 1, Bewegungslehre, 2 Aufl. B., 1921; PC’S chi Th., Lehrbueh d. technischen Mrehanik, B., 1923; Beyer R., Einfilhrung in d ie К inematik, Lpz., 1928; Perry J., Angewandte Meelianik. Lpz., 1908; Kennedy A., The Mechanics of Machinery, L., 1907; Hartmann W., Kin neues Verfahrea zur Aufsucliung des Kriimmungskrcises, «Z. d. VDI», 1893, p. 95; Kutzbach, «Maschinenbau». Berlin, 1927. Л. Смирнов.