> Техника, страница 61 > Механика теоретическая

Механика теоретическая

Механика теоретическая, учение о движении материальных тел. Если какое-либо тело с течением времени изменяет свое положение по отношению к какому-либо другому телу, называемому телом (системою) отсчета, то говорят, что первое тело находится в состоянии движения по отношению ко второму, в отличие от состояния покоя, когда относительное положение тел остается неизменным. Т. о. понятие движения содержит в себе понятие пространства, времени, перемещающегося объекта и системы отсчета. Понятия пространства и времени, являясь предметами исследования философии, обычно предполагаются в М. т. данными. Что касается перемещающегося объекта, то в действительности он не всегда является материальным телом, например перемещающаяся тень, смещение силовых линий в силовом поле и тому подобное. Движение материальных тел называется движением корпускулярным. М. т. занимается изучением только корпускулярных движений. Обычно изучение движения материальных тел начинают с изучения движения материальной точки. Под материальной точкой подразумевают в М. т. тело произвольной величины при наличии по крайней мере одной из следующих предпосылок: когда все линейные размеры тела ничтожно малы по сравнению с расстояниями от рассматриваемого тела до других тел, играющих роль в данной проблеме, или когда вращение тела не принимается во внимание, а рассматривается лишь движение центра массы (центра тяжести)тела (смотрите Центр тяжести). Так например, рассматривая движение земного шара вокруг солнца, можно землю принимать за материальную точку, чего нельзя делать, рассматривая движение земли вокруг ее оси. Установив законы движения материальной точки, выводят затем из них законы движения системы отдельных материальных точек и сплошных материальных сред (континуумов). Допустимость последнего перехода в последнее время однако подвергается сомнению. Если все точки данной совокупности, или системы материальных точек, сохраняют свои взаимные расстояния неизменными, то система называется твердой, в противоположном слу чае—нетвердой. В частности, если материальные точки системы заполняют определенный объём, то такая система точек называется т е л о м—твердым или нетвердым в зависимости от вышеуказанных признаков. В качестве системы отсчета обычно берут твердое тело, с которым неподвижно связаны три взаимно перпендикулярные пересекающиеся в одной точке прямые Ox, Оу, Oz, называемые осями координат. На практике телом отсчета чаще всего служит земля или какое-либо твердое тело, неподвижно с ней связанное.

Из предшествующего следует, что понятия движения и покоя суть понятия относительные и что, поскольку все известные нам системы отсчета сами находятся в движении по отношению к другим телам отсчета, нельзя говорить ни об абсолютном движении ни об абсолютном покое их. Если бы хотя одно тело находилось в состоянии абсолютного покоя, то можно было бы судить как об абсолютном, так и об относительном характере движения всех прочих тел. В .19 в эфир— носитель световых и электромагнитных явлений—считался, за исключением малых колебаний его, абсолютно неподвижным. Этим самым создавалась такая система отсчета, по отношению к которой всякое движение могло быть названо движением абсолютным, а покой—абсолютным покоем. Эта точка зрения в корне опровергается современной теорией относительности, которая в числе прочих своих заключений приходит к выводу, что даже в области электромагнитных явлений не представляется возможным отличить «абсолютный» покой от равномерного йоступательного движения системы. В связи с коренной ревизией понятий пространства и времени, совершенной теорией относительности Эйнштейна, М. т., основы которой были положены Ньютоном и которая называется классической, рассматривается в настоящее время как частный случай более общей системы М. т., называемой релятивистской. Выводы классич. М. т. справедливы лишь как первые приближения для корпускулярных движений, происходящих со скоростями, ничтожно малыми по сравнению со скоростью света. В дальнейшем здесь излагаются основы лишь классич. М. т.

Обычно М. т. разделяют на кинематику, статику и динамику. В кинематике рассматривают только геометрия. свойства движения, не принимая во внимание действующие силы. В статике рассматривают те условия, которым должны удовлетворять данные силы, чтобы система, к которой они приложены, находилась в покое. В динам и к е изучается зависимость между силами и соответствующими движениями системы материальных точек. Статику и динамику объединяют часто в один отдел— кинетику. Часто в М. т. выделяют особый отдел, т. н. геометрию масс, изучающую свойства распределения массы системы в пространстве; сюда относятся связанные с центром масс, с моментами инерции (смотрите) и тому подобное. вопросы.

Кинематика, рассматривает законы движения тел независимо от действующих сил.

Движение какой-либо совокупности или системы материальных точек, в частности движение твердого тела, определяется движением всех точек, составляющих систему, вследствие чего является необходимым исследовать сначала свойства движения отдельной точки и затем лишь свойства движения какой-либо совокупности их.

Пусть имеется точка А, движущаяся по отношению к некоторой системе отсчета, состоящей из 3 взаимно перпендикулярных осей координат 0$, Оу, Oz, имеющих начало в точке О. Каждое положение точки А по отношению к заданной системе координат определяется некоторой тройкой отрезков х, у, z, взятых со знаками (+) или (—) или, что равносильно, нек-рым радиусом-вектором г, имеющим начало в О, а конец в рассматриваемом положении точки А, причем г=(1)

где г_х—единичный вектор (орт), определяющий направление О А, а г—численное значение этого отрезка (модуль). При движении точки А координаты ее х, у, z с течением времени изменяются, так что для данного движения имеют место три функциональные зависимости между координатами точки А и временем ί:

x=fi(t), У-hit), z=h(t). (2)

Последние ур-ия, характеризующие данное движение точки А, называются уравнениями движения. Т. к. при движении точки А радиус-вектор г изменяется с течением времени, то г—также нек-рая ф-ия ί: г=r(t)=хг + yj + zle, (3)

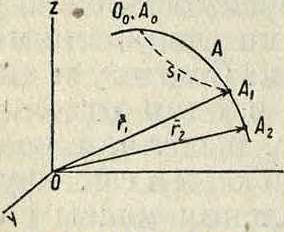
где i, j, Те—единичные векторы, определяющие направление осей координат, причем последнее векторное ур-ие вполне заменяет собою три ур-ия движения (2). Совокупность всех положений точки в пространстве при данном ее движении называется траекторией. Если траектория—плоская кривая, то и движение называется плоским; в этом случае для определения движения точки достаточно двух осей координат—Ох и Оу, взятых в плоскости движения. Если траектория представляет собой прямую линию, то движение называется прямолинейным; в последнем случае для определения движения точки достаточно одной оси координат Ох, совпадающей с прямолинейной траекториейточки. Прямолинейность или криволинейность движения суть также понятия относительные,зависящиеот состояния,.в котором пребывает сама система отсчета. На траектории следует различать две особые точки: начало отсчета 0₀ длины s кривой (где s=0) и начальное положение А₀ точки А, то естьто ее положение, при к-ром начался отсчет времени (ί=0). В целях упрощения часто берут однако начало отсчета длины О₀совпадающим с начальным положением А₀ точки (фигура 1), так что ^О₀А₀=0. Каждому определенному моменту ί соответствует определенное значение величины s=^w.4₀n₁,TaK что s есть нек-рая ф-ия от ί:

«-/(О- (4)

Фигура 1.

Если на оси асбцисс отложить отрезки, пропорциональные истекшим промежуткам времени ί, а по оси ординат отрезки, пропорциональные s, то геометрическое место получившихся точек—некоторая кривая, которая называется графиком пройденного пути (фигура 2). Пусть в момент ί_χточка А находилась от О₀ на расстоянии O₀n₁=s₁, считаемом по длине кривой,

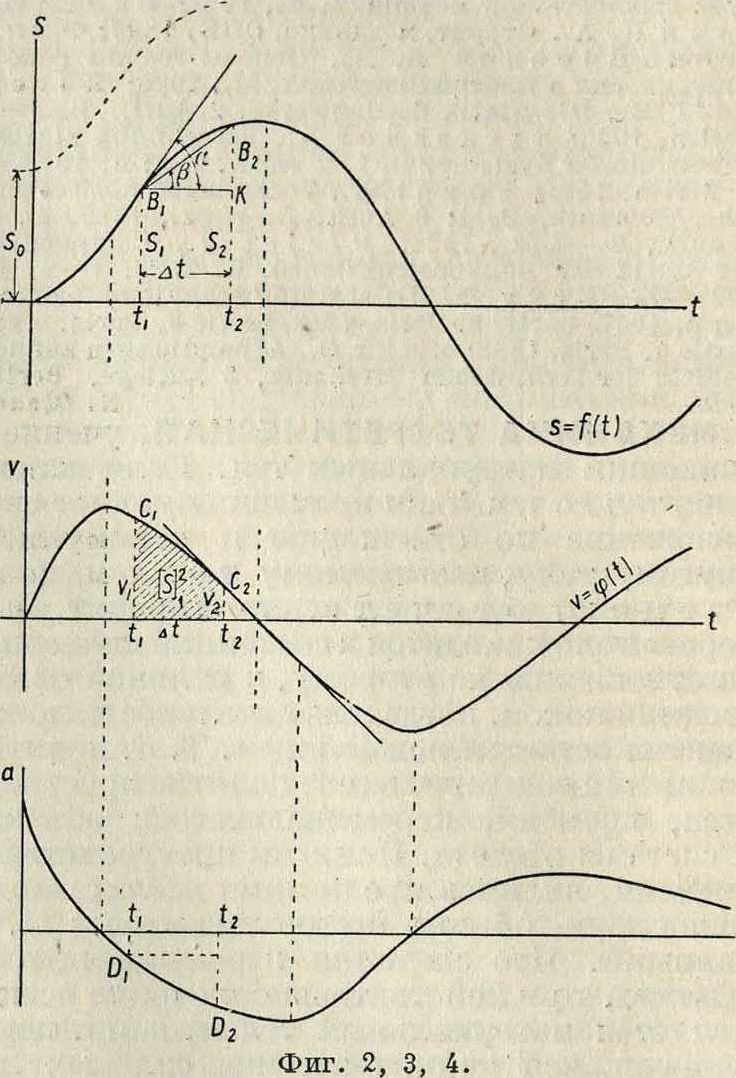
а в некоторый последующий момент ί₂ на расстоянии 0₀А₂=s₂, так что за промежуток времени i₂ — ί _х=Δί точка прошла по своей траектории путь s₂ — s_x=As. Средней линейною, или скалярною, скоростью v_cP точки А за промежуток времени Δί называется частное от деления As на Δί, т. ч.

^υ°ρ· ~Tt‘ (5)

Если обозначить на графике пути точки, соответствующие положениям А_х и А₂, через jBj и В₂, то v_cp. равняется тангенсу угла, образуемого отрезком В_гВ₂ с положительным направлением оси ί:

V,

ср.

^is ₌ ёзК _{= t}g β. в, к

At

(6)

Линейною, или скалярною, скоростью v в данный момент называется предел отношения когда Δί стремится к 0, т. e. υ равняется производной s по переменному ί:

Очевидно в общем случае υ есть также некоторая ф-ия от ί:

v=?>(<). (8)

Из ур-ия (7) нетрудно видеть, что на графике пути

v=tga, (9)

где а есть угол, образованный касательной, проведенной к кривой в соответствующей точке, и положительным направлением оси t. Если способом, аналогичным вышеприведенному, построим кривую, выражающую функциональную зависимость (8), то получим т. наз. график скорости (фигура 3). Интегрируя ур-ие (7), получаем:

s=fvdt + C=f <p(t)dt + С, (10)

откуда также следует, что путь |s|f, пройденный точкой за промежуток времени от

ДО ΐ2 5

s l=jvdt=j<p(t)dt. (11)

11 U

Так как выражение, стоящее в правой части ур-ия (10), представляет собой на фигуре 3 площадь, ограниченную ординатами, проходящими через точки t_t и ί₂, частью С_гС_гкривой и осью абсцисс, то эта площадь и равняется численно пути js|J. Из ур-ия (9) не трудно также видеть, что экстремальным точкам графика пути соответствуют точки пересечения графика скорости с осью ί, а точкам перегиба первой кривой соответствуют экстремальные точки второй. Если в частности v — Const=V, то такое движение называется равномерным. В последнем случае имеем из ур-ия (10):

s=Vt + С. (12)

Если, при ί=t-ι, s=s_v то, т. к. C=s_x— Fi_1;имеем:

s-W-tJ + S!. (12)

Очевидно в этом случае график скорости будет представлен прямой, параллельной оси f, а график пути—прямой, наклоненной под углом а к оси ί (фигура 5), так что

tg α= V. (13)

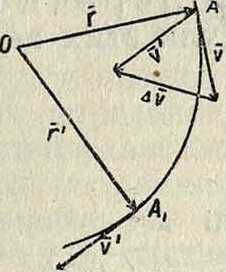
Пусть в нек-рый момент ί движущаяся точка находилась в положении А, определяемом по отношению к данной системе от-счета радиусом-ве-

1ч₉п ктором г, а в не-

-1-f который поеледую-

₅ щий момент t=t +

+Δί—в положении А, определяемом радиусом-вектором г== г+Аг. Средней скоростью v_sp. точки за промежуток времени Δέ называется выражение

(14)

Истинною скоростью v точки в момент ί называется предел отношения (14) πριιΔί->0, то есть производная вектора г по времени ί:

-Ϊ5,©- ‘А<‘⁵>

Т. к. направление Аг в предельном положении совпадает с направлением касательной, проведенной к траектории в рассматриваемом положении точки, то направление v совпадает с направлением этой касательной; т. о. единичный вектор v₁ определяет также и направление касательной tj, так что

V=ντ₁. (16)

Фиг.

Т. к. далее г“=гг_и то из (15) имеем:

dr _ d (rrj) di di

dr, dri

= dT^ri + ^r dt

T. о. вектор скорости м. сумма двух векторов:

dr

^V>-=dt ^Г1

. dr.

(17)

представлен как

(18)

dt

(19)

причем первый вектор имеет направление, определяемое а второй — вектором то есть вектором, перпендикулярным к первому. Скорость v_r называется радиальной скоростью, а скорость v_p — трансверсальной, или поперечной, скоростью. Так как

^drl ^dv _п

dt dt —’

(20)

где ψ—угол поворота г около О, а р_х—единичный вектор, перпендикулярный г_г, то

dq>

^vr-^rdtPi-

(21)

Абсолютные значения этих скоростей очевидно следующие:

dr

dt ⁹

dq>

Vr=-

^vP=^rdt

(22)

(23)

откуда имеем также:

’-V (£f+I4rr· (»)

Т. к. параметры г и φ суть полярные координаты точки А (смотрите Координаты), то (24) представляет собою выражение скорости в полярных координатах. Если в частности точка А перемещается в пространстве так, что 7*i=Const, то есть если А перемещается по прямой, проходящей через О, то, так как в этом случае=0, из ур-ий (17—19) имеем: v_P=0; v=v_r**^r₁ (17)

dr _

di

(17")

Величина г играет в этом случае ту же роль, что и величина s в формуле (7), и следовательно формулы (10), (11) и (12) применимы и для прямолинейного движения с соответствующей заменой длины кривой s длиною прямолинейного отрезка г. Если же, наоборот, г= Const, то очевидно, что точка движется по шаровой поверхности. В этом случае

v_r=0; v=v_p=r^d/.p₁ и

dt- “

В частности точка может перемещаться по кругу. Пусть в этом случае точка переместилась за промежуток времени Δί по дуге А<р, длина которой As. Если Αφ выражена в радианах, а г—радиус окружности, то очевидно As=r Αφ. Частное ~ называется средней угловою вращения точки:

At

скоростью ω

α>,„.=,

Αφ At ’

Предел ω_α]>. при Δί-»0 называется угловой скоростью вращения со точки в момент <:

lim /М d<p it

Т. о. (17”) м. б. в рассматриваемом случае представлено еще в следующем виде:

V=г · ω. (18)

Угловая скорость м. б. представлена вектором ω, проведенным из центра вращения перпендикулярно плоскости движения в такую сторону, чтобы наблюдатель, помещенный вдоль вектора, видел вращение точки происходящим по часовой стрелке. Если за промежуток времени Δί угловая скорость

. Δω

изменилась на Δω, то частное называется средним угловым ускорением точки: в_ср. Предел этого отношения при Δί -> 0 называется угловым ускорением Θ в момент ί:

я ₌ Пт /М ₌ ^dm.

Δί-»0 Δί dt

Если θ=Const, το движение называется равнопеременно вращательным, если же со=Const, то движение называется равномерно вращательннм.

Рассмотрим движение проекций точки А по трем взаимно перпендикулярным осям координат Ox, Оу, Oz. На основании (17") скорости этих точек при их движении

- dx dy dz по соответствующим осям будут

С другой стороны, модули проекций скорости V на эти оси на основании (7):

ds

υ_χ=V COS α= - COS а

ν_υ=г> cos /3=^ cos β

, U9

ν_ζ=ν cosy =, cos γ

(25)

где α, β, γ—углы, образованные вектором ν с положительными направлениями осей координат; т. к. ds cos α= dx, ds cos β=dy, ds cos y=dz, то из (18) имеем: i, dx Vx ~~ ~~ di

V«=VJ =

V_a=V_Z =

dy

dt

dz

dt

(26)

T. e. скорости проекций точки А на три оси координат равняются соответствующим проекциям скорости на эти же оси. Эти проекции скорости называются ее к о м-понентами по рассматриваемым осям. При условии ортогональности осей имеем:

Зная ур-ия движения (2), можно ф-лы (26) и (26) написать еще и так:

v_y=v_z=fi(t)·,

ν=vxw)?+m)Y + ит^г.

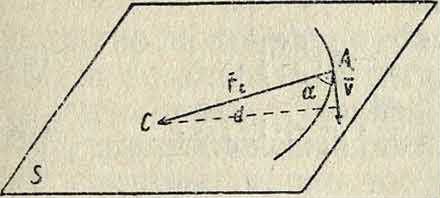
Моментом скорости ν по отношению к некоторой точке С называется вектор, модуль которого равняется произведению ν на длину d перпендикуляра, опущенного из С на линию действия ν, а направление определяется направлением перпендикуляра, восставленного к плоскости S, образованной ν и С, в такую сторону, чтобы наблюдатель, помещенный вдоль него в точке С, видел ν направленным по часовой стрелке (фигура 6). Т. к. длина перпендикуляра d, или плечо, равняется d=rsina, где а—угол между ν и г_е, то, обозначая момент скорости через М, имеем: Μ — ν d=v - г- sin а

M-lv-rJ. (27)

Помещая начало отсчета О в точке С, имеем г_с=— г, где г=С А, и следовательно

М=[г ν]. (27)

Рассмотрим площадь Ао, ометаемую подвижным радиусом-вектором г за промежуток времени Δί до положения его г, так что 4- (г, г)=А<р. Предел отношения _Д( при Δί -»О называетсясекториальной скоро с т ьто ν точки; т. о.

^<28>

Секториальная скорость м. б. представлена в виде вектора ν, проведенного перпендикулярно к плоскости, проходящей через г кг, где г—последующий во времени радиус-вектор, бесконечно близкий к г, причем обычно направление ν выбирают так, чтобы наблюдатель, помещенный вдоль ν в начале отсчета О, видел вращение г происходящим по часовой стрелке. Так как

do— ^r²d<p=^lds, (29)

где ds—длина элемента дуги, а I—длина перпендикуляра, опущенного из О на ds то, принимая во внимание (28) и (23), имеем:

гИтК·¹· (зо)

Т. к., с другой стороны, do=[г dr]|, то

(31)

и следовательно, принимая во внимание (27), получаем:

2v=М, (32)

т.е.момент скорости ν относительно нек-рого центра равен удвоенной секториальной скорости движущейся точки относительно того же центра. Если отложить от одной и той же точки векторы скорости движущейся точки при различных ее положениях, то геометрич. место концов этих векторов образует кривую, называемую годографом скорости (смотрите).

Пусть за промежуток времени Δί линейная скорость изменилась на величину Αν. Средним линейным, или скалярным, ускорением а_ср. называется частное ^, так что

(33)

Линейным, или скалярным, ускорением а точки А в момент ί называется предел отношения (33) при Δί-» 0, то есть производная ν по времени ί:

^аср- Д( ·

или, принимая во внимание (7),

Средним

d(2

полным,

(35)

или средним векторным, ускорением назы-где Αν—изменение ско-

вается частное

At

рости V за промежуток времени At, так что

(36)

Полным, или векторным, ускорение м а в момент ί называется предел отношения (36) при Δί 0, так что

·-&©-£ (^з7>

Так как а_ср.—вектор, направленный внутрь кривизны кривой (фигура 7), то и полное уско-

ФИГ. б.

Фигура 7.

рение а всегда направлено внутрь кривизны траектории. Принимая во внимание (15), имеем также

(38)

или, принимая во внимание (3), имеем:

a-^d2x i i ^d‘v j i ^d2z ί.

^a dt* * ⁺ dt* 9 + _dt% ^K·

Таким образом вектор а равен сумме следующих трех компонент, направленных по осям координат:

<22“. °^х ~ ап *’

d*z,

^а*=оп^к·

у ап-

Модули этих векторов, равные

<2²х _ а²у _ d*z

dt*’ ^ау dt*’ ап’ представляют линейные ускорения проекций точки на осях координат. При α= Const движение называется равноперемен-н ы м; при этом, если а > 0, то движение называется равноускоренным, если же а < 0, то движение называется равнозамедленным. При α= Const движение очевидно будет не только равнопеременным, но и прямолинейным. Далее при «=Const имеем из (34) и (7):

Jdv =J*adt; v=at + C_u (39)

s=fvdt=f(at + C₁)dt= at²+C₁t+C₂, (40)

где C₁ и С_г суть некоторые произвольные постоянные, которые м. б. определены, если величины v и s, соответствующие каким-нибудь определенным значениям t, даны. Так, если в начальный момент, то есть при ί=0, v=v„, s=s₀, то из (39) имеем С_г=ν₀, а из (40) C₂=s₀, так что ф-лы (39) и (40) принимают следующий частный вид:

v=г>₀ + at, (39)

s=s₀ + v₀t + ₂ at²

(40)

Если построить кривую, выражающую функциональную зависимость (34) между а и ί, точно таким же способом, каким выше был построен график скорости, то мы получим график ускорения (фигура 4). Т. к. на основании (34) и (7) между а и v существует точно такая же зависимость, как между v и s, то между графиками ускорения и скорости существует очевидно точно такая же связь, как между графиками скорости и пути. Т. о. имеем: 1) тангенс угла наклона отрезка С_гС_г, соединяющего две точки С_г и С₂графика скорости, равняется среднему линейному ускорению за соответствующий промежуток времени; 2) тангенс угла наклона касательной, проведенной к графику скорости, равняется линейному ускорению точки в соответствующий момент; 3) площадь, ограниченная дугой И_гИ₂ графика ускорений, ординатами, проходящими через точки ί_χ и ί₂, и осью t, численно равна приращению скорости за промежуток времени Δί от ij до ί₂; 4) точкам пересечения графика ускорения с осью ί соответствуют экстремальные точки графика скорости, а экстремальным точкам первой кривой соответствуют точки перегиба второй. Если в частности движение равнопеременно, то график ускорений представляет собой прямую, параллельную оси ί (фигура 8). График скорости представляет в этом случае на основании (39) наклонную прямую, отсекающую на оси v отрезок равный г>₀ и имеющую tg угла наклона равный а

"т;-

4 -ί

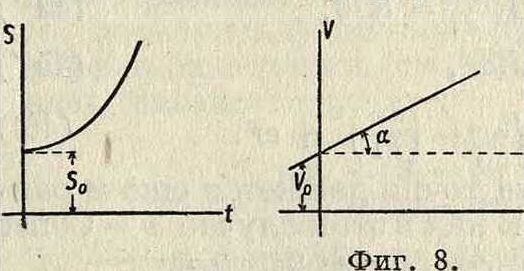
a, a график пути на основании (40)—параболу, имеющую своей осью ось ординат и отсекающую на последней отрезок s₀.

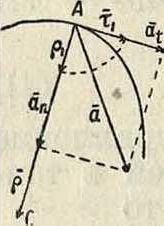
Пусть радиус кривизны траектории в точке А равен ρ (фигура 9), а направление центра кривизны С от 4 определяется ортом ρ_χ, так что

АС=ρ=ρρ₂. (41)

Если т_х—орт, определяющий направление касательной, проведенной к кривой в точке А в сторону возрастания дуг, то

άτι

ds

где * —кривизна траектории в точке А. Из (16), (42) и (7) имеем следовательно:

(42)

dv ά(ντι) dv

αν —. άτ₁ αν

= 47 ^τι+»7Τ -7Ηι

dv

dt

dt

dt

dv -,

= di^ +

dt

Qv

άτχ ds ^J ds dt

(43)

Таким образом вектор ускорения равняется сумме двух векторов

dv И

υ²

Ct/_n

6

Qi>

(44)

(45)

причем первый вектор имеет направление, определяемое т_х, то есть имеет направление касательной, а второй—направление ρ_1; то есть направление от А к центру кривизны С. Первый вектор называется поэтому тангенциальным ускорением, а второй— нормальным ускорением. Модули этих векторов соответственно равны:

«%-ff. (440

«_я=у. (450

а линейное ускорение

«-/(1)417 ^(4в)

Из (43) видно, что вектор а лежит в плоскости, образованной касательной и главной нормалью, то есть лежит в соприкасающейся плоскости. Т. к. бинормаль перпендикулярна к этой плоскости, то компонента по бинормали а_ь всегда равна нулю:

«6=0. (47)

Если точка движется прямолинейно, то

ρ=со, и по (45) имеем а_п=0, так что в этом случае α= a_t=~ П и α= a_t=^j. Если к тому же точка движется еще и равномерно, то α= 0, то есть ^=0. Если точка движется по окружности радиуса h, то, так как ρ=R== Const, из (44"), (45) и (46) следует:

(44") (45") (46)

Если к тому же точка движется еще и равномерно, то, так как в этом случае v=Const

“ И ⁼ 0, ^из (44), (43) и (45) имеем:

у 2

«ί=0; α= а_п=— ρ_λ=βω²·ρ₁·

Т. о. при равномерном круговом движении полное ускорение в любом положении точки а_п= Reo²1

Фигура 9.

направлено по нормали, то есть направление а все время проходит через центр окружности. Последнее движение представляет собой частный вид т. п. центральных движений, то есть таких движений, при которых направление полного ускорения в любом положении точки проходит через один и тот же центр. Из формул (17), (20) и (21) имеем далее:

‘-5г-г(£->) + £0· §?*)-

d.r_l ! dr άφ dt

dp i dt

d*r dr

dt* ^{1 :} dt

dt _dtPi + ^rj£pi +

A__riv

¹ dt

(48)

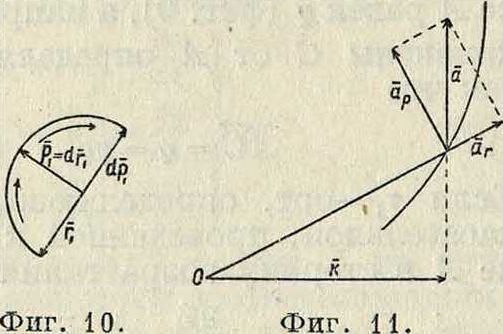
Так как Pi ± r_lt a dpi _L Pi, причем p_г и dp_xвращаются от r₁ в одну и ту же сторону (фигура 10) и так как | dp_x |=άφ, то

dpi _·άφ "dt dt ¹’

так что (48) принимает следующий вид:

Т. о. вектор а разложен на две компоненты:

^аг= {Ζ~^τ{ηΪ}^ ⁽⁵⁰⁾

и

ct_n

из которых первый, имеющий направление г_иопределяет радиальное ускорение, а второй вектор, имеющий направление, перпендикулярное к первому, определяет поперечное ускорение. Так как модули этих векторов

(50) (51)

a =^dlr-r(^d?Y ^ar dt2 ^r dt] ’

О dr άφ, К ^ap dt dt^~^r dt* ^:

, ά²φ

ТО

»-/ЙМЭТ+ PSd+S]·. <*>

что дает выражение а в полярных координатах г и φ. Секториальным ускорением μ называется производная по времени от секториальной скорости v, т. ч.

μ=%· (53)

Принимая во внимание (30) и (51), имеем из (53):

μ =

1 d

2 dt

и так как

ra_v=ka,

где k — расстояние от О до линии действия а (фигура 11), то

μ=2^а · к. (540

Если движение центральное и если начало отсчета взять в центре движения О, то в этом случае линия действия а в любой момент должна проходить через О, и значит /г=0 и μ=0, а следовательно v=Const. Таким образом при всяком центральном движении секто-риальная скорость постоянна, то есть, другими словами, площадь, ометаемая подвижным радиусом-вектором, пропорциональна времени. Нетрудно доказать также, что всякое центральное" движение—движение плоское.

Исследовав законы движения отдельной точки, можно перейти к исследованию движения механической системы точек, то есть такой совокупности их, в которой движение каждой точки определенным образом зависит от движения остальных. В частности механич. система называется системой твердой, если взаимные расстояния точек при движении системы остаются неизменными. Допустим, что система состоит из п точек. Т. к. положение каждой точки определяется 3 координатами, то положение всей системы определяется 3п координатами ХъУь ,x₂,y_t, г_ьх_п,у_п, г_п. При движении системы все эти координаты суть нек-рые ф-ии времени t. Зависимости между точками системы обусловливаются силами взаимодействия их или связями, то есть такими условиями движения, которые налагают ограничения либо только на положение точек либо также на их скорости. В первом случае связи называются геометрическими, а во втором — кинематическими. Каждая геометрич. связь выражается ур-ием вида:

/(жi, Ух, *х, ®«> У 2, *:а, •••.ж», Уп, z_n, t)=0, (55) а кинематич. связь—ур-ием вида:

<р(хX, Ух,	, Ζι,.	·» Упi
άχχ dyi	dzi	о II N ·£
dT’ ~dt’	W’ "

(56)

Допустим, что между п точками данной механической системы существует к геометрических связей:

/гО*т, Vi, &х, ···, ж_и, у_п, ζ_η, t) О

(i-1, 2,3,. fc). ⁽ ’

Тогда из Зи координат Зп— к будут независимы, а остальные к координат определяются через них из ур-ий (57). Эти независимые координаты называются также координатами системы; число их определяет так называемую степень свободы системы (смотрите Координаты).

Всякое движение твердой системы точек, и в частности твердого тела, м. б. сведено к двум основным видам движения: поступательному и вращательному. Поступательным движением называется такое движение, при к-ром любая прямая, соединяющая две какие-либо точки системы, остается во время движения последней параллельной сама себе. Так, если прямая, соединяющая точкиД и В, занимала положение Πι-Βχ, то спустя промежуток времени она займет положение Д₂В₂II Д1-В1· Так как

А г_А=Дгв, (58)

где

Аг_л=А₁А₂; Аг_в=В_гВ₂,

ТО

lim (		= lim (	LrB
Δ(-»0	V Δί	Δί—»0	At

т. e.

v_A=V_B. (59)

T. о. при поступательном движении все точки системы имеют в данный момент равные скорости. Очевидно, что при поступательном движении траектории всех точек системы представляют собой конгруентные кривые. Способом, аналогичным вышеприведенному, получим, что а_А=^ав, (60)

то есть что полные ускорения всех точек системы в данный момент между собою равны.

Вращательным движением тела называется такое движение, при к-ром две из его точек, АиВ, остаются неподвижными. Нетрудно видеть, что в этом случае и все точки, лежащие на прямой АВ, называемой осью вращения, будут также неподвижны. При вращательном движении очевидно каждая точка, за исключением точек, лежащих на оси вращения, движется в плоскости, перпендикулярной к оси вращения,по окружности, центр которой находится на этой же оси.

Угол поворота Δφ тела за какой-нибудь промежуток времени Δί определяется дуговым перемещением какой-нибудь из его точек за тот яге промежуток времени, вследствие чего угловая скорость со и угловое ускорение & какой-либо точки тела определяют соответственно эти же величины и для вращающегося тела. Угловая скорость м. б. вышеуказанным способом представлена при помощи вектора со на оси вращения тела. Пусть движущаяся точка вращающегося тела занимает на окружности положение А, определяемое по отношению к началу отсчета О, взятому на оси вращения, радиусом-вектором г (фигура 12). Так как по (18) ν=Ь со, где b — радиус окружности, и так как Ь —=г sin (α>, г), то

»=cor sin (со, г) (61)

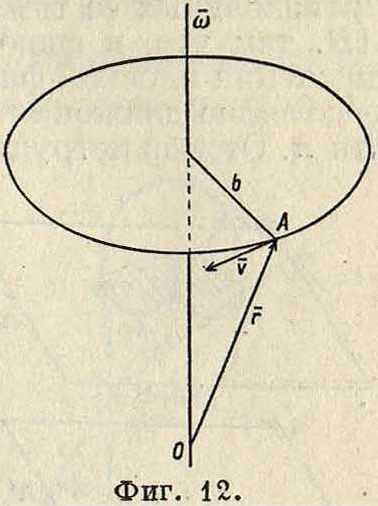
и следовательно

V=[со т. (62)

Если модули проекций вектора со на три произвольные ортогональные оси координат с началом О обозначим через ·ρ, q, г, а модули проекций г на те же оси через х, у, г, то, пользуясь формулой проекции векторного произведения (смотрите Векторное исчисление), имеем:

V_x=qz-ry

v_y=rx — pz > · (63)

v_z -vy- qx)

Это—t. h. ф-лы Эйлера. В общем случае век тор со меняет как величину, так и направление, определяемое ω₁, и каждому моменту времени соответствует определенная мгновенная ось вращения. В частности со может менять лишь свой модуль, то есть менять лишь свою угловую скорость, сохраняя одну и ту же ось вращения. В последнем случае вращательное двиягение называется перманентным.

Плоскопараллельным движением твердого тела называется такое eio движение, когда все точки тела описывают плоские траектории, лежащие в плоскостях, параллельных некоторой неподвижной основной плоскости. В этом случае очевидно имеем: 1) все точки тела при своем движении остаются на неизменном расстоянии от основной плоскости’, 2) если данное тело находится в плоскопараллельном движении по отношению к плоскости π, то оно находится в таком яге движении и по отношению к любой другой плоскости π, параллельной первой (фигура 13). Следовательно можно основную плоскость π всегда выбрать так, чтобыонапересекала данное тело по нек-рому контуру К. Зная положение контура К на теле и в основной плоскости, можно определить и положение тела в пространстве. Т. о. исследование рассматриваемого движения тела сводится к исследованию движения контура К в плоскости л, то есть, что то же самое, движения подвижной плоскости р, связанной с К, в плоскости л. С другой стороны, положение плоской фигуры, ограниченной контуром К, в пло-скбсти л определяется положением двух произвольных ее точек А к В или отрезком АВ, так что в свою очередь определение движения плоской фигуры К сводится к определению движения отрезка АВ в плоскости л. Отсюда нетрудно прийти к следующим

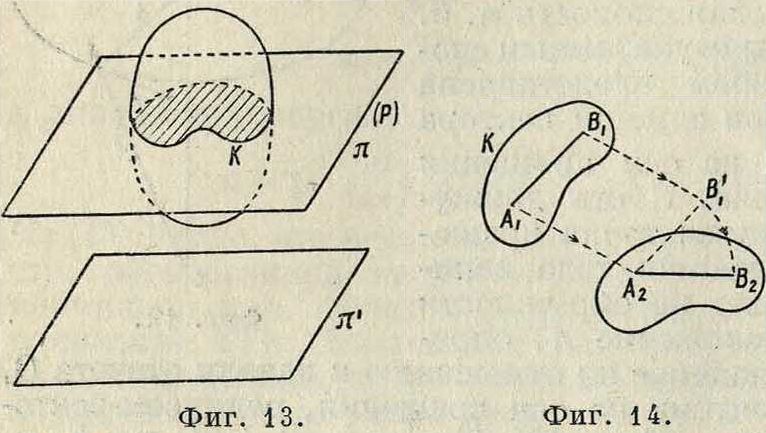
выводам: 1) Из любого предшествующего положения плоской фигуры К, находящейся в плоскости л, можно привести ее в любое последующее положение в той же плоскости при помощи одного поступательного и одного вращательного движения, или наоборот. В самом деле, если первое положение фигуры определяется положением отрезка АЯЗ^ (фигура 14), а второе положение—тем же отрезком, но в положении А_гВ₂, то можно сначала переместить отрезок А_гВ_г параллельно самому себе до А₂В[, а затем повернуть последний отрезок до положения А₂В₂. При первом движении отрезка плоская фигура будет перемещаться поступательно, а при втором—· вращательно. Порядок этих движений очевидно м. б. изменен. 2) Из всякого положения плоской фигуры в плоскости л можно

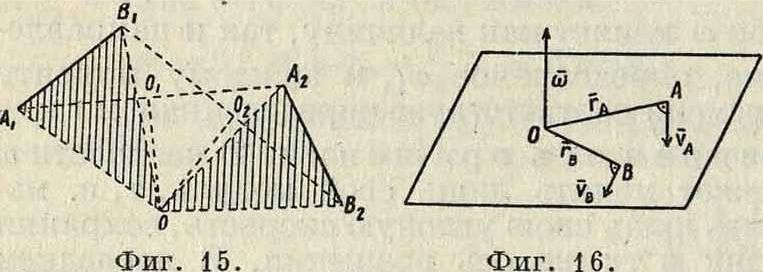
привести ее в любое другое положение в той же плоскости при помощи одного вращения около нек-рого центра О. В самом деле, пусть имеются два положения плоской фигуры, определяемые положениями А_гВ_г и А₂В₂ отрезка АВ, так что А₁В₁=А₂В₂ (фигура 15). Проведя прямые А_гА₂ и В_гВ₂ и восставив из их середин О_х и 0₂ перпендикуляры, получим в пересечении этих перпендикуляров точку О; АА₁ОВ₁=АА₂ОВ₂, т. к. AJl^ — А₂В₂, А₁0=А₂0, BjO=B₂0. Т. о., вращая АА₁ОВ₁ около точки О, можно его привести в положение А₂ОВ₂, то есть привести А₁В₁ в положениеИ₂В₂. Точка О представляет собой центр вращения, соответствующий двум рассматриваемым отдельным положениям плоской фигуры. Если центр вращения соответствует двум бесконечно близким положениям плоской фигуры, то он называется мгновенным. Мгновенный центр вращения занимает определенное положение как в плоскости л, так и в плоскости р, переме щающейся вместе с фигурой. Т. к. движение плоской фигуры состоит в непрерывном переходе от одного положения к бесконечно близкому к нему другому положению, то этому движению соответствует бесконечно большое число мгновенных центров вращения, непрерывно следующих друг за другом. Геометрии. место мгновенных центров вращения в плоскости л называется неподвижной полодией, или центроидой, а в плоскости р—п одвижной полодией. Эти кривые соприкасаются всегда в точке, представляющей мгновенный центр вращения в данный момент. Если же бесконечно малое вращение происходит около мгновенного центра вращения 0₂, то принадлежащие плоскостям ли р две точки О и Οί, совпадавшие в предшествующем центре вращения Oj, разойдутся; при этом ^0(0₂=w0"0₂; это указывает на то, что при движении плоской фигуры подвижная полодия перемещается, и притом без скольжения, по неподвижной полодии. Каждому определенному движению фигуры соответствует определенная пара полодий. Если подвижную полодию сделать неподвижной, а неподвижную—подвижной, то движение плоскости л по отношению к р называется движением обращенным по сравнению с первым. В общем обращенное движение совершенно отлично от данного. Так, если прямая перемещается в плоскости, касаясь данной окружности, то каждая точка подвижной плоскости описывает эвольвенту круга, а если, наоборот, окружность катится по прямой, то каждая точка плоскости описывает циклоиду. Траектория какой-либо точки подвижной плоскости р по отношению к неподвижной л называется рулеттой.

Угловая скорость вращения плоскости р около мгновенного центра вращения называется мгновенной угловой скоростью. Очевидно все точки плоскости обладают в данный момент одной и той же мгновенной угловой скоростью. Пусть имеем в плоскости р две точки А и В, положение которых относительно системы отсчета с началом в мгновенном центре вращения О определяется г_А и г_в. Из ур-ия (62) имеем:

VA=i^wrAV, «в=[йГгд], (64)

где ν_Α и v_B—скорости точек 4иБв данный момент (фигура 16). Т. к. со ±г_Л и ω 1 г_в, то из уравнения (64) имеем также: ν_Λ=т_А, υ_Β=ων_Β и

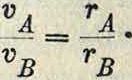
(65)

Т. о. из ур-ий (64) и (65) имеем: 1) скорости всех точек плоскости р перпендикулярны к прямым, соединяющим их с мгновенным центром вращения; 2) величины скоростей пропорциональны расстояниям от соответствующих точек до мгновенного центра вращения. Отсюда следует далее, что концы векторов скоростей для точек прямой, проходящей через мгновенный центр вращения О (фигура 17), лежат на прямой, также проходящей через О, т. к. лишь в этом случае величины векторов скоростей v_lt υ·_ζ,. пропорциональны расстояниям А_гО, А₂0,. Если повернуть векторы скорости v_A и v_B (фигура 18) в одну и то

^гх ^тв ту же сторону на 90°, то получаются т. н. ортогональные скорости v_A и,v^. Т. к. на основании ур-ия (65)

- “ ”4§ ^vb

^ТА ^ГВ

Отсюда следует, что, соединив концы А и В ортогональных скоростей, получаем прямую АВ, параллельную АВ. Это соображение дает легкий способ построения скорости и любой другой точки С. Для этого достаточно соединить С с А и В и из точек А и В провести прямые АС I! АС и АВ II АВ;

--У

СС=гадает ортогональную скорость точки С, так что, повернув г>£на 90° в сторону, противоположную прежней, получим v_G. Очевидно, если С лежит на А В, то С лежит на АВ. Т. о., если прямая д (фигура 19) не проходит через мгновенный центр вращения, то концы векторов ортогональных скоростей точек прямой д лежат на одной прямой, параллельной д, причем все ортогональные скорости пересекаются в точке О. Проектируя ортогональные скорости v_A, v_B, νβ,. на перпендикулярное к д направление д_п, получим одинаковые проекции, и т. к. эти скорости

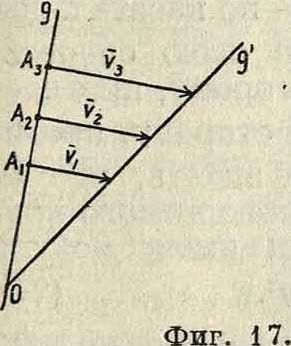
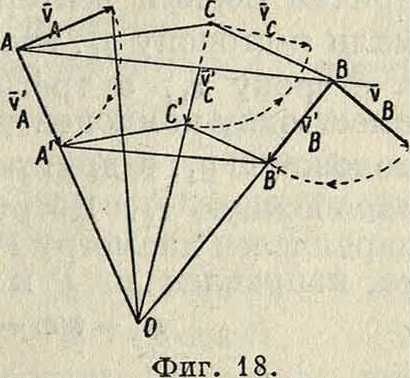
суть повернутые на 90° истинные скорости v_A, v_B, Vc и т. д., то проекции последних по направлению д также равны между собой.

Что касается ускорения точек плоскости р, то, так как по ур-ию (46) ускорение каждой точки зависит от радиуса кривизны ρ ее траектории, необходимо предварительно рассмотреть зависимость между д и другими элементами движения. Возьмем какую-нибудь точку плоскости, перемещающуюся по траектории Т (фигура 20), и рассмотрим два бесконечно близких положения ее при увеличении времени на величину dt. Нормали ЛК и АК, восставленные к Т в точках 4и4, пересекаются в центре кривизны К и пересекают неподвижную полодию S в точках Р и Р. Пусть AP=l; РК=с; w РР= da; w АА =ds; далее АКА=άτ; АРА=d<p; 4-NPA=а, где ΝΡ нормаль к S в точке Р. Проведя радиусом КР дугу РВ, имеем:

W РВ do · COS а КР С ,ЛЛ

——— == у——» (66)

К А ^г±^с

^ AA

ds

причем знак минус следует взять, если К лежит между Ри4; так как ds=I d<p, то

da COS а с „„„ (1, 1 „„„ „ άφ 1

i * —i— “ - ИЛИ ( ~ di ^ ) COS СС — -Z--, · (67)

άφ I 1±с с 1) da d ⁴

Величины в левой части ур-ия (67) зависят от выбранной на плоскости р точки, в то время как имеет в данный момент одно и то нее значение для всех точек р, вращающихся около мгновенного центра Р. В следующий момент ~ изменит в общем свое значение,

но новое значение опять будет одним и тем

άφ

же для всех точек р, так что есть нек-рая ф-ия от ί. Т. к. I и а суть полярные координаты точки А, то геометрии, место точек, для которых Const, есть проходящая через точку Р окружность с центром на нормали N,

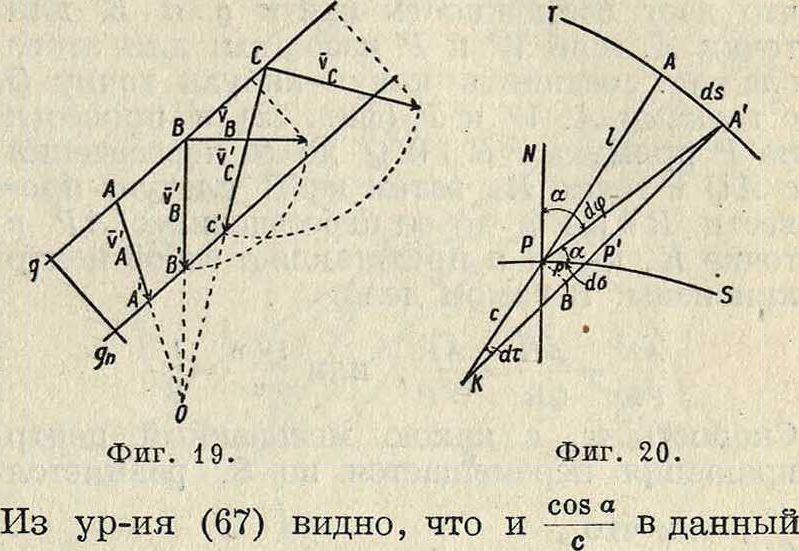
момент также постоянно для всех точек, для которых и —г—=Const, то есть представляет также окружность. Обе эти окружности соприкасаются в той Hie точке Р, что и полодии. Т. о. центры кривизны траекторий всех точек, лежащих на окружности, проходящей через Р, также лежат на окружности, проходящей через Р. В частности, если Р1£==с= оо, то из ур-ия (67) имеем:

— - а,

COS а ⁹

(68)

что представляет собой геометрии, место точек, траектории которых имеют в данный момент ρ= со, то есть точек, проходящих в данный момент через точки поворота. Геометрии. место точек, представляемое ур-ием (68), есть окружность диаметра d. проходящая через Р и называющаяся поворотным кругом. Соответствующая поворотному кругу окружность=Const превратилась в бесконечно удаленную прямую. Если на поворотном круге взять какую-ни

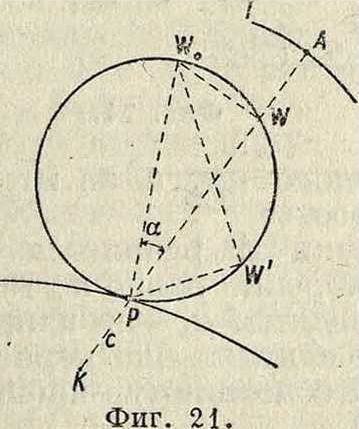
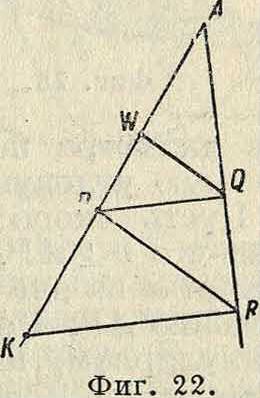
будь точку W (фигура 21), то т. к. мгновенное вращение точки W происходит около Р, то есть в направлении, перпендикулярном к WP, отрезок W₀W, дающий направление поворотной касательной, проходит через W₀— крайнюю точку диаметра d поворотного круга, называемую полюсом поворота. Т. о. все поворотные касательные проходят через точку W₀. Проведя из точки А

плоскости р прямую АР, на которой лежит и центр кривизны К траектории Т, и обозначив PW=и, имеем и= d cos а, a из уравнения (67) получаем:

- ± 1=¹

с ~ I и

ИЛИ

¥=(69)

что дает возможность найти ρ и К для точки А, если W и Р известны; для этого следует соединить какую-нибудь точку Q с точками A, W и Р (фигура 22) и провести из Р прямую PR, WQ до ее пересечения с AQ в точке Е, затем из Е следует провести RWKPQ до ее пересечения с АР в точке К, которая и представляет собой центр кривизны. В самом деле,

AK^AJ₌AP _или!±‘ ₌ ‘.

РК QR WP ^{с и}

Скорость w, с какою мгновенный центр вращения перемещается по £, равняется

da

dt

так ЧТО

da dt

(70)

Эту скорость не следует смешивать со скоростью точки Р, принадлежащей плоскости р и имеющей скорость равную 0. С другой стороны, имеем:

так что, деля (70) на (71), имеем на основании ур-ия (67):

d=^w · (72)

Т. о. скорость перемещения мгновенного центра вращения равняется произведению

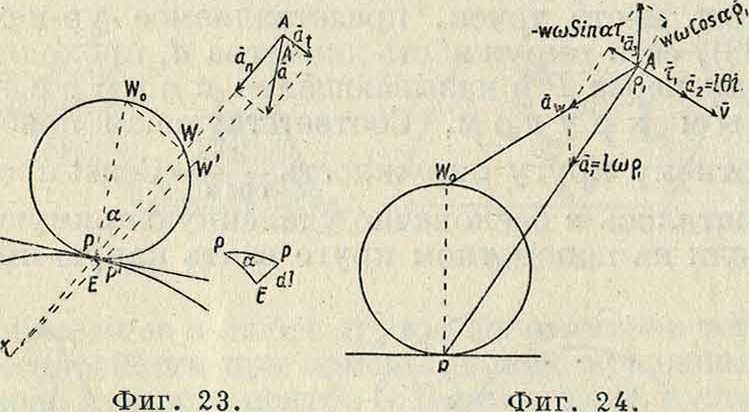
из диаметра поворотного круга на мгновенную угловую скорость.

Пусть скорость точки А равняется ν, так что ν _L АР, а ускорение равно а. Разлагая а на две компоненты: а_п—по направлению АР, а щ—по направлению перпендикулярному, имеем на основании ур-ия(45): 1*012 _ 12

_ V² АР² со2 ^α,ί в е²

(+ с

(73)

или, т. к. на основании ур-ия (69)

AW~ 1-и =

1 + с ’

то a,=AW · ω²; с другой стороны, AW== АР — WP=l — d cos а, так что на основании ур-ия (72)

а_п=(I — d cos а) ω²=Ιω² — ινω cos α. (74)

Из ур-ий (44) и (18) имеем также:

dv

"Ш^в

а,

d((ol) dl, ₇ do>

^ν =ω—+Г

dt

dt

dt

При перемещении точки из И в И прямая АК пересекает S уже в новой точке Р, так что РР=da, а отрезок I=АР уменьшается на величину РЕ= dl (фигура 23); следовательно

dl da.. j.

,=— Jr Sin α=— wsino=- ω· d sm α.

at at

Таким образом со² sin a=Z0—Wcu sin a, (75)

где θ—мгновенное угловое ускорение плоскости р, или, пользуясь (44) и (45), имеем из (74) и (75):

α= (Zco² — vxd cos а) -f- (Ιθ — vxo sin α) ϊω²ρ₁ -f- ΙΘ ту — vxo cos a · — ινω sin a Tj. (76)

T. о. а состоит из трех компонент (фигура 24):=Ιω^ιρ_χ i

α₂=ΙΘ τ, (77)

α₃=— ww COS α · ρ₁ — ινω sin α · τ₁) причем первый вектор направлен по нормали в сторону ρ_χ, второй—по касательной в сторону т_1; а третий, в свою очередь, имеет одну компоненту в сторону, противоположную ρ_1; а другую—в сторону, противоположную τ₁. Нетрудно видеть, что а₃параллелен Диаметру PW₀ поворотного круга, направлен от Р к W₀ и имеет модуль

(77)

а₃=vxo=d со².

Так Kaii⁰¹=~

то, взяв результирующую направлен-

“з w₀p ‘

a_w~^ai + а₃, получим вектор, ный от А к W₀, причем

a_w=AW₀-(D (78)

Т. о. полное ускорение м. б. представлено еще и как сумма двух векторов a_w и а₂:

α= + а₂. (79)

Ускорение а_ъ называется полюсным ускорением. Модуль «з, как видно из (77), один и тот же для всех точек. Это есть в то же время ускорение той точки плоскости р, которая совпадает с Р и которая имеет следовательно скорость=0. Ускорение a_w называется поворотным ускорением. Т. к. всем точкам поворотного круга соответствуют радиусы кривизны их траекторий равные оо, то поворотный круг есть в то же время геомет-рич. место всех точек, нормальные ускорения которых а_п== 0. Для того чтобы найти геометрич. место точек, для которых тангенциальные ускорения равны 0, то есть для которых a_t= 0, имеем из (75):

ΙΘ — d cu²-sin α=0; -¹—=^d=h. (75)

’ Sina β ⁴

Так как в правой части (75) имеется выражение, постоянное для всех точек р, то (75) представляет собой окружность, диаметр которой h=_g.^- перпендикулярен к нормали N и проходит через Р. Из сравнения (75) и (68) видно, что найденная окружность, называющаяся кругом перемен, пересекает поворотный круг в некоторой точке В, не имеющей ни тангенциального ни нормального ускорения, то есть в точке, полное ускорение которой равняется нулю. Точка В называется поэтому центром ускорений. Определение центра ускорений В имеет большое значение при определении ускорений точек плоскости р. Так как A- W₀PB=A- W₀HP=β (фиг 25), то из (75) имеем:

(⁷⁵")

Ускорение а точки А можно разложить на две компоненты « и а" по направлению АВ и по перпендикулярному к АВ направлению, для чего, разложив а_п и щ по этим двум направлениям, сложим соответствующие компоненты. Обозначая

A W₀PA=а; * W₀PB=A W₀HP=β АВАР=γ; ALBP=d, имеем, принимая во внимание (74), (75) и (72):

α= а_п cos y — a_t sin γ=(Ζω² — wco cos a) cos γ — — (Ιθ — wa> sin a) sin γ=Ζ(ω² cos γ — θ sin γ) —

— dco² cos (α + γ), (79)

a"=α_η sin у + a_t cos γ=Ζ(ω² sin γ + θ cosy) —

— d of- sin (a + γ). (80)

Опуская из P перпендикуляр на AL, имеем:

PL=Z sin γ=BP sin δ=d cos β sin δ. (81) Принимая во внимание (81) и (75"), имеем из (79) и (80) после соответствующего пре образования:

а= ω² (Z cos у —d cos/? cos d), (82)

a"=Θ (Z cosy — d cos/Scos d). (83)

Но выражения, стоящие в скобках правых частей последних равенств, равняются АВ=е, так что окончательно имеем:

α= βω², (84)

а"=ев, (85)

α^βΫω^+θ². (86)

Кроме того а а

Θ

С02

⁼ tg β·

Из (86) видно, что величина ускорения любой точки плоскости р пропорциональна расстоянию е точки до центра ускорения, а направление полного ускорения образует один и тот же угол β с прямой, соединяющей точку с центром ускорения.

Возвращаясь к плоскопараллельному движению тела, нетрудно прийти к заключению, что мгновенному вращению плоской фигуры около мгновенного центра Р соответствует мгновенное вращение тела около оси, перпендикулярной к π и проходящей через точку Р. Т. о. подвижной и неподвижной полодиям соответствуют две цилиндр, поверхности, пересекаемые плоскостью π ортогонально, так что в сечении получаются данные полодии. Цилиндрич. поверхность, проходящая через подвижную полодию, называется подвижной аксоидой, другая же поверхность называется неподвижной аксоидой. Плоскопараллельное движение тела происходит следовательно так, как будто подвижная аксоида, неподвижно скрепленная с телом, катится без скольжения по непод вижной в пространстве аксоиде, причем общая образующая представляет в данный момент мгновенную ось вращения. Если данное тело движется так, что одна точка О остается неподвижной, то, описав в теле около этой точки О шаровидную поверхность S,

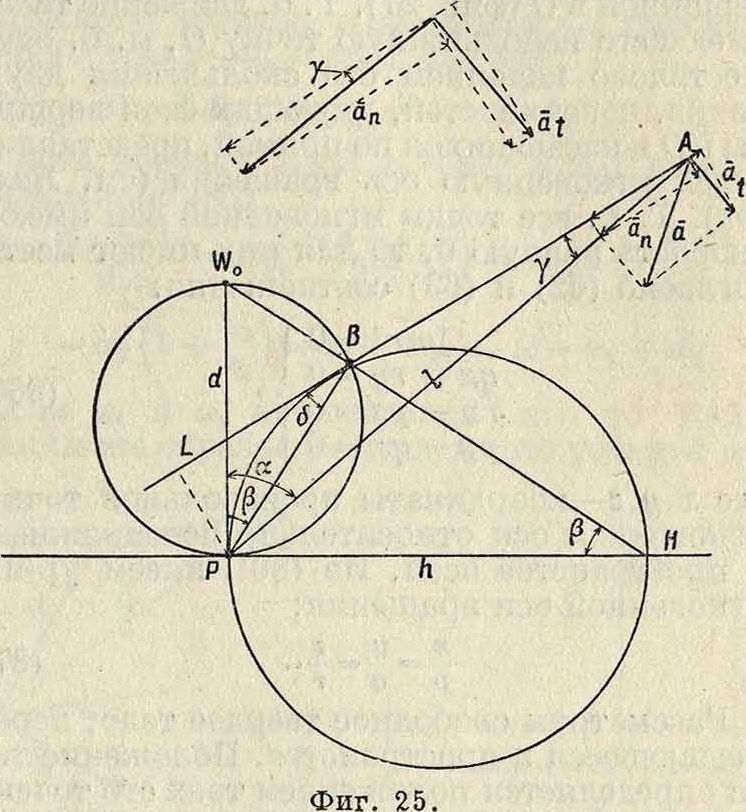
можно определить положение тела в пространстве, зная положение S, так что изучение движения тела сводится к изучению движения поверхности S. Положение же последней определяется положением дуги большого круга, проведенной по шаровой поверхности между двумя какими-либо точками последней. Пусть эта дуга перешла за какой-нибудь промежуток времени каким-нибудь образом из положения П₁В₁ в положение А₂В₂(фигура 26). Соединив точки А_г, А₂ и В_1г В₂дугами большого круга и восставив к серединам С_г, С₂ последних перпендикулярные дуги большого круга, найдем нек-рую точку О пересечения последних, находящуюся также на поверхности S. Соединив О с Hj,©! и с А ₂, В₂ дугами большого круга, получим два, равных сферических тр-ка _{Фиг- 2}б.

А₁0В₁ и А₂рВ₂.

Закрепляя точку О на поверхности S, можно, вращая тр-к HjO ’В_г, привести его в положение А₂0В₂, что очевидно равносильно вращению всей шаровой поверхости S около оси ОО. Т. о. из всякого любого предшествующего положения в любое последующее можно рассматриваемое тело привести при помощи одного вращения около некоторой оси, соответствующей этим двум положениям. Если тело переходит из одного положения в бесконечно близкое к нему другое положение, то соответствующая ось вращения называется мгновенной. При движении тела мгновенные оси вращения, проходя через точку О и следуя непрерывно друг за

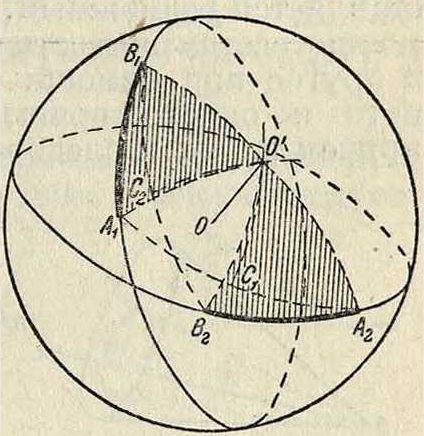
другом, образуют в пространстве нек-рую конич. поверхность с вершиною в О, представляющую неподвижную аксоиду. Геомет-рич. место мгновенных осей вращения в самом теле, то есть подвижная аксоида, представляет очевидно также конич. поверхность с вершиной в О (фигура 27). Т. о. движение тела, имеющего неподвижную точку О, м. б. осуществлено качением без скольжения двух конич. поверхностей, имеющих свои вершины в О и касающихся по прямой, представляющей мгновенную ось вращения (смотрите Волчок). Т. к. все точки мгновенной оси имеют скорость равную 0, то для них имеют место согласно (62) и (63) соотношения:

[со г]=О qz — ту=О rx — pz=О ру — qx=О

где х,у,z—координаты произвольной точки мгновенной оси относительно неподвижных в пространстве осей. Из (86) имеем ур-ия мгновенной оси вращения:

^ж=Д=^г. (87)

р ч г ⁴

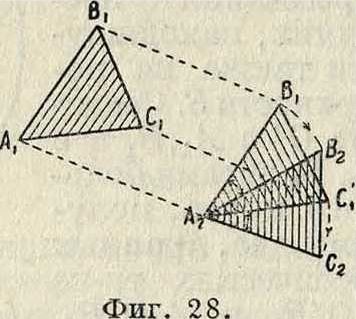
Рассмотрим свободное твердое тело, перемещающееся в пространстве. Положение тела определяется положением трех его точек, не лежащих на одной прямой, то есть положением нек-рого тр-ка АχΒ^. Пусть тело пришло из положения, определяемого тр-ком ΑιΒ^ν в положение, определяемое треугольником А₂В₂С₂ (фигура 28). Из первого положения во второе можно было бы привести тело след, обр.: переместив тело поступательно по направлению А_гА₂ до совпадения точек Αχ и А2 так, чтобы тр-к А₁В₁С₁ занял положение A₂B[Ci, повернуть затем тело около некоторой оси, проходящей через А₂ так, чтобы тр-к А₂В₁С₁ совпал с тр-ком А₂В₂С₂, что на основании изложенного всегда представляется возможным. Т. о. свободное тело можно всегда привести из одного положения в другое при помощи одного поступательного и одного вращательного движения, причем порядок следования движений роли

Фигура 27.

не играет. Отсюда следует, что и бесконечно малое перемещение тела м. б. представлено бесконечно малым вращением и бесконечно малым поступательным движением, которые могут происходить одновременно. Совокупность поступательного и вращательного движений называется винтовым движением. Ось вращения называется осью винтового движения. Если эти движения бесконечно малы, то винтовое движение называется мгновенным. Т. о. при своем движении свободное тело в каждый момент совершает нек-рое мгновенное винтовое движение, причем в общем винтовые оси меня ют свои положения как в самом теле, так и в пространстве. Геометрии. место винтовых осей, то есть подвижная аксоида, представляет собой нек-рую линейчатую поверхность, соприкасающуюся по прямой с другой линейчатой поверхностью — неподвижной ак-соидой. Общая образующая представляет собою мгновенную винтовую ось. Примером таких линейчатых поверхностей могут служить два однополостных гиперболоида, соприкасающихся по одной прямой (фигура 29), причем если один из них неподвижен, то

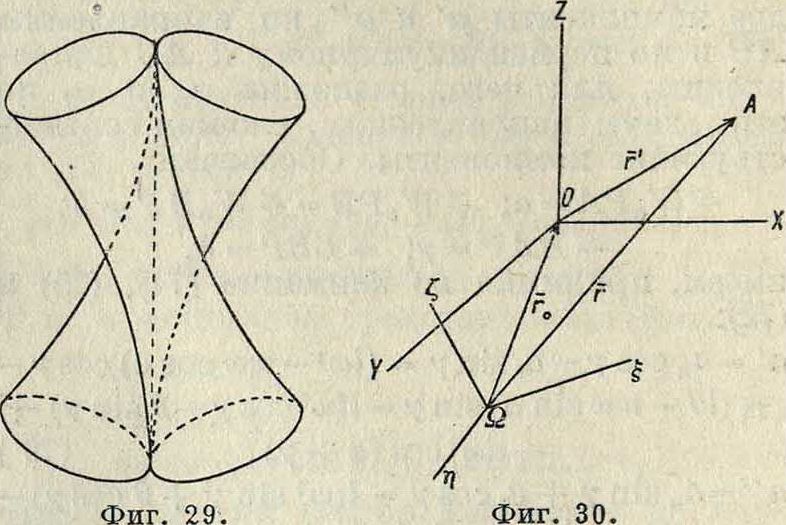
другой может перемещаться по поверхности первого, совершая около общей образующей бесконечно малое вращение и скользя в то же самое время вдоль нее, вследствие чего мгновенная винтовая ось называется также мгновенной осью скольжения-вращения (смотрите Винт в теоретической механике и Мбторное исчисление).

Пусть некоторое тело перемещается по отношению к некоторой системе отсчета Oxyz, которая вместе с телом перемещается по отношению к системе отсчета Ωξηζ, так что каждая точка тела принимает участие в двух движениях: по отношению к Oxyz и вместе с последней системой по отношению к Ωξηζ. Движение тела по отношению к первой системе называется относительным, движение Oxyz по отношению к Ωξηζ—п е-реносным, а движение тела по отношению к Ωξηζ—движением сложным. Два первых движения называются составляющими -движениями. Число составляющих движений м. б. и больше двух. Скорости в этих движениях носят соответствующие этим движениям названия: относительной, переносной и сложной скоростей. Пусть радиусы-векторы, определяющие положение А по отношению к Oxyz и Ωξηζ будут ν’ и г, а радиус-вектор, определяющий положение О по отношению к Ωξηζ будет г_а (фигура 30), т. ч. г=г + г₀, (88)

откуда имеем:

dr

dt

dr

Ж

dr q

dt

(89)

Обозначая относительную, переносную и сложную скорости точки А тела соответственно через v_r, v_e и v, имеем:

dr. ^: dt’

drо. dr

^Ve=W’ ^{V =}

так что из (89) имеем:

v=v_e+ v_r,

(90)

(91)

то есть вектор скорости в сложном движении равняется сумме векторов скоростей состав-

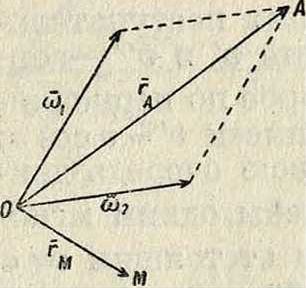
ляющих движений. Составляющими движениями м. б. движения поступательные, вращательные, винтовые и тому подобное. При различных видах составляющих движений получаются различные виды сложных движений. Пусть тело в своем относительном движении перемещается поступательно со скоростью v_x, а система Охуг вместе с телом движется также поступательно, но со скоростью г>₂. Т. к. v_xи ν·2 в данный момент постоянны для всех точек тела, то каждая из них также имеет одну и ту же сложную скорость v, то есть сложное движение также поступательно. Если составляющие движения представляют собой мгновенные вращения, векторы мгновенных угловых скоростей которых суть ω_χ и е>₂, то могут представиться такого рода случаи: 1) оси вращения пересекаются, 2) оси вращения параллельны и 3) оси вращения перекрещиваются. Если оси вращения пересекаются, то, рассматривая скорость вершины А (фигура 31) параллелограма, построенного на со_х и со₂, смещенных в О, имеем из (62): “ 0₂)д=ΙΑ nil-

так что

ν_Α=[«й ^ГА~ + К Г Ah

где г А=о А,

но так как

!>ι г_А]=- [ω₂ г_А], то ν_Α - О, так что А в данный момент находится в покое,—другими словами, вся прямая О А также находится в покое, и следовательно сложное движение представляет собою мгновенное вращение, происходящее около диагонали О А. Пусть мгновенная угловая скорость сложного движения равна Ω. тогда скорость сложного движения какой-либо точки М будет

^vm — [*Ω ^гм -> (91)

с другой стороны, по (91) имеем:

•’ll=+ [о>а ^гмЛ=[(«i + ®₂) «*дг]; (92)

сравнивая (91) и (92) получаем:

Ω=ω_χ + ω₂. (93)

Обобщая этот результат для случая п составляющих мгновенных вращательных движений, можно написать: ·

Й- (i-¹» 2,3, .,η). (94)

i=l_

Пусть далее ω₁ : ω₂ и направлены в одну и ту же сторону. Проведем плоскость, jnep-пендикулярную к ω_χ, пересекающую ω₁ в точке А_х, а со₂—в точке А₂ (фигура 32). На прямой А_ХА₂ можно найти такую точку А, которая имела бы в данный момент сложную скорость, равную нулю. В самом деле, пусть С—некоторая точка на А_ХА₂; тогда скорость относительного движения С будет (v_x)c =

= [со_хА_хС], а переносная скорость (v₂)_c =

= [ω₂ А₂С], причем направления этих векторов противоположны. Т. о. для нахождения А имеем:

ω_χ А_ХА=ω, · А, А, или ₌^ai ₌ -f^^A, (95)

^{11 2 2} ’ ·"* А, А

так что А делит А_ХА_% внутренним образом на части, обратно пропорциональные ω_χ и со₂. Очевидно все точки, лежащие на прямой ΑΌ ω_χ, имеют также v=0, так чтэ AD есть мгновенная ось вращения сложного движения. Пусть мгновенная угловая скорость сложного вращения равняется Ω. Рассматривая точку А₂, имеем для нее:

(v)j₂=Ω АА₂; (у_х)_л>= со_х А^_ Ыд₂=0.

Таким образом Ω АА₂=со_х · А_ХА₂, или на основании (95):

Ω=“н ^AlAs=a>J= cujfl + ^AAi)=aa₂ a₂a i a AA_SI

^{= ω}ί[¹ + ^)^==ωι + ^ωΤ, Ω=ω_χ+ω₂.

Если ω_χ и ω₂ антипараллельны, то точно таким же образом получаем, что точка А де-

о

Ω=ώ₍*·ώ,

Фигура 31.

Фигура 32.

лит отрезок А_ХА₂ внешним образом на части, обратно пропорциональные ω_χ и со₂, и что Ω=со₂ — ω_χ (если со₂ > coj). В последнем случае, если а>₂= — ю_х (пара вращений), то мгновенная ось вращения удаляется в бесконечность, и тело в своем сложном движении перемещается поступательно со скоростью, перпендикулярной к плоскости, образованной ω_χ и со₂. В самом деле, для какой-либо точки М тела имеем (фигура 33):

v=К Р_ХМ] + К РТМ]=К (Р_ХЖ -Р^М)] =

= [си_х Р_ХР₂] и v=со_х Р_ХР₂. (96)

Точно такую же скорость v будет иметь и любая другая точка тела. Отсюда следует,

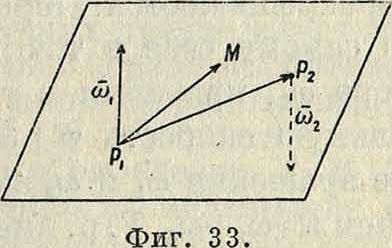
Фигура 34.

что всякое поступательное движение тела м. б. рассматриваемо как составное движение пары вращений.

Пусть далее одно из составляющих движений будет мгновенное вращение, а другое движение—поступательное, перпендикулярное к мгновенной оси вращения. Заменим скорость v поступательного движения парою вращений со_х и со₂ так, чтобы ω_χ=ω=—ω₂(фигура 34), причем на основании (95) имеем:

1 Р₂=—;

т. к. со₂=—со, то эти два вращения взаимно уничтожаются, и остается одно вращение <о_х.

Т. о. сложное движение в данном случае есть мгновенное вращение, происходящее с мгновенной угловой скоростью, равной данной, но около оси, параллельной первой и отстоящей от нее на расстоянии. Если мгновенная ось вращения не перпендикулярна к скорости V поступательного движения, образуя с последней угол а, то раз

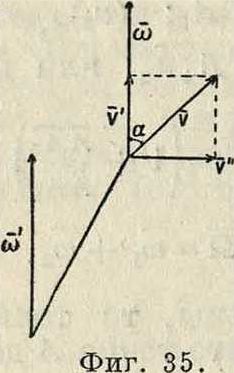
ложив V на два составляющих поступательных движения со скоростями ν и ν"—первое по направлению со, а второе по перпендикулярному направлению—имеем v=v cos а; ν"=v sin а (фигура 35). В свою очередь движения ν" и ω м. б. заменены одним мгновенным вращением со II со и отстоящим от ω

, ν" ν sina

на расстоянии α= ~ =-----; в окончатель-

ω О)

ном итоге имеем сложное движение, состоящее из поступательного движения со скоростью ν и мгновенного вращения с угловой скоростью со, причем со II ν, то есть получаем мгновенное винтовое движение.

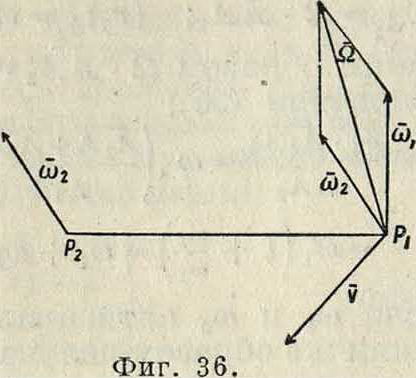
Пусть наконец имеются два мгновенных вращения с угловыми скоростями со₂ и со₂, на

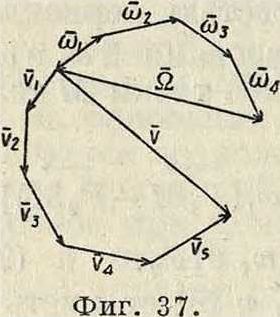
правления которых перекрещиваются. Перенося со_а параллельно самому себе в точку приложения вектора co_lt прибавим в то же время поступательную скорость ν±ω₂(фигура 36). Мгновенные вращения ω_χ и со₂ заменим одним вращением i2=co₁-l-co₂. Т. о. имеется вращение Ω и поступательное движение ν, которые м. б. заменены, как выше было доказано, одним винтовым движением. Обобщая вышеприведенные результаты, можно сказать, что если имеются п мгновенных составных вращения ω_ν со₂, ., ω_η и m составных поступательного движения %, v₂, .,v_m, то, заменив все составляющие вращения одним результирующим вращением ii (фигура 37), а все поступательные движения одним результирующим поступательным движением со скоростью v, заменим затем Ω и v одним результирующим винтовым движением.

Определение полного ускорения точек тела при сложном движении последнего м. б. произведено след. обр. Пусть обе системы отсчета Оий имеют одно общее начало и пусть мгновенная угловая скорость вращения системы О будет со; скорость какой-либо точки А, определяемой радиусом-вектором г, складывается из переносной скорости [сог] и относительной скорости v_r, равной, где знак () указывает на то, что изменение рассматривается по отношению к системе О (т. н. локальная производная). Т. о.

»=£ =[«»·] + £. (97)

Так как всякий другой вектор b=Ь (ί) м. б. рассматриваем как радиус-вектор конечной точки его, то и по отношению к b м. б. применено соотношение (97), то есть

£-[“4+!γ О⁷)

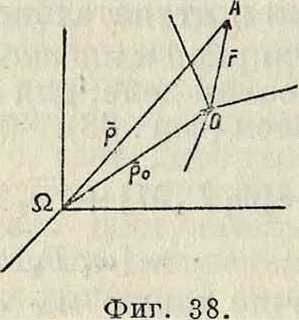
Если же начало О не совпадает с началом

£2, то, обозначив О А=г, ΩΟ — ρ„ и ΩΑ=е (фигура 38), имеем:

8=So + **· (⁹⁸)

Отсюда, на основании (97) имеем:

^v=⁺ί^ων1 ⁺ Χт ^{= г,}° + +*V.(99)

где v₀ — скорость точки О. Беря производную по t от (99) и применяя к v_r и г формулу (97), имеем:

+ [-S +=+ КН +

+ [ω + [ω [tu г]] + + [со v_r],

dr

или же, так как ^=v_r, имеем после приведения:

*“1и +ЙН + [«[“*·]] +

+ 2 [со «,.] +^· (100)

Если бы не было относительного движения, то, так как v_r=0, ускорение а равнялось бы ускорению переносного движения а_г, и следовательно.

^а-Ж+Ш *·]+[“> <¹⁰¹)

член представляет очевидно относи тельное ускорение

dv_r^: dt

(102)

Таким образом

α= а_е + а_г + 2 [со v_r]; (ЮЗ)

последний член правой части (103) представляет т. н. добавочное или п о в о р о τη о е (кориолисово) ускорение а_с, так что а_с=2 [со ν,.] (104)

и а_с=2со · v_r sin (со, ν,.). (105)

Динамика точки. До сих пор явления движения рассматривались нами вне зависимости от «причин», вызывающих их, то есть вне зависимости от тех факторов, без наличия которых данное движение не могло бы состояться, каковы например мускульное усилие руки при бросании нами предмета, притяжение земли, натяжение нити при качании маятника и тому подобное. Зависимости, существующие между данными «причинами» движения или силами и вызываемыми ими движениями, составляют предмет изучения динамики. В основу последней положены следующие принципы, нашедшие свое подтверждение в совпадении полученных на их основе теоретич. выводов с фактич. явлениями природы. 1) Всякая материальная точка, на которую никакая сила не действует, находится в состоянии прямолинейного и равномерного движения (так называемым принцип инерции, или 1-я аксиома Ньютона). В этом случае имеем очевидно -<)

V=Const,

т. ч. характер движения точки определяется равенствами (12) и (12)· 2) Всякая сила, действующая на материальную точку, сообщает последней ускорение, пропорциональное величине силы; направление же полного ускорения а совпадает с направлением действующей силы F (2-я аксиома Ньютона). Обозначая постоянный для данной материальной точки фактор пропорциональности между а и К, характеризующий также массу точки, через т (смотрите Масса), имеем следовательно:

^Fa=т (106)

И

F=та или по (37) и (15)

т dv d²r

^F=mdt^=mdTP

(107)

Проектируя F на три взаимно-перпендикулярные оси координат Ox, Оу, Oz и обозначая эти проекции через X, Т, Z, имеем из (2) и (38):

d*x.

X=ma_x=пг г×= ma_y=т ^d^j

ГЖ d^z-.

Z=ma_z=т-^к

Х—ш

d²x

dt%

• или Y=rn^| i>- (108)

Ур-ия (108), равносильные ур-ию (106), называются основными уравнениями динамики. Обозначая углы, образованные вектором F с положительными направлениями осей координат,через а, β, у,имеем:

cos α= р cos/S= ^; cosy=J!; (109)

F=VX~ + Y² + Z²; (ПО)

что дает возможность определить величину и направление силы, зная величины X, Υ, Z. Так как одновременное динамич. воздействие X, X, Z эквивалентно действию F, то X, Y, Z называются поэтому компонентами, или составляющими, силы F по осям координат. Аналогично этому проекция F по какому-нибудь произвольному направлению называется ее компонентой, или составляющей, по этому направлению. Пусть к данной материальной точке приложены силы F_lt F₂,., F_n, компоненты которых по осям координат суть соответственно X_t, Х^, Ζ_χ, Χ₂, Τ2, Ζ₂, ., Χ„, 1 „, Ζ_η ·

Заменив силы, действующие по одной и той же оси, равнодействующими X, X, Ζ, имеем:

Х=|]х_г; Х=2Х_г; Z~^Z_t.

1 1 1 Вектор F, компоненты которого по осям координат суть X, X, Z, называется равнодействующей данной системы сил F_x, F_t, ., F_n, а последние называются силами составляющими. Т. о. имеем:

F=JC+ Х+Х=(Х₁ + Х₂-Ь.+Х_Я) +

+ (Х₁+Х₂+.+ Х_и) + (Z₁+Z₂ + .+ Z„)== № + ΐι + ζ_χ) + (Х₂ + Х₂ + Ζ₂) +. +

+ (Х_в + Y_n + Z_n)=F_x + F₂ +. + F_n, (110) т. e. вектор равнодействующей силы равен сумме векторов сил составляющих. Мн-к ΑΒίΒ₂Β₃. Я,₍(фигура 39), построенный так, что

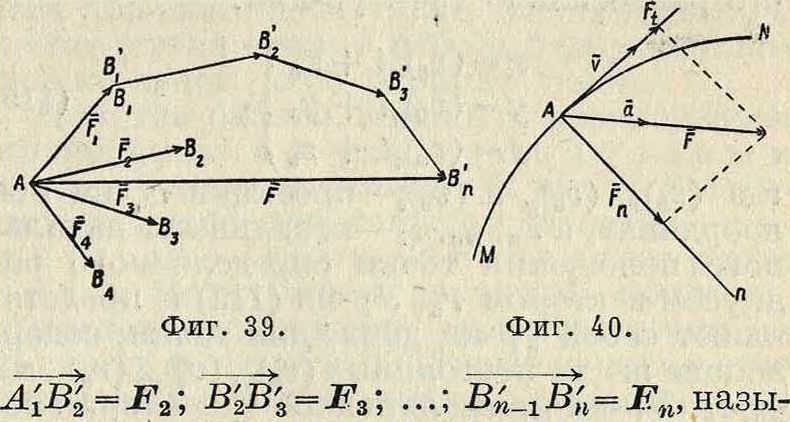
вается многоугольником сил, или силовым многоугольником. Вектор F очевидно равен замыкающей стороне силового мн-ка, проведенной от начала мн-ка А к концу его Βή· Из (110) имеем в этом случае:

^=|/(2^х*)+(|]^у*)+ (|]Z(-).(110")

Пользуясь ур-иями (108) или, что равносильно, ур-ием (106), можно себе поставить следующие две основные проблемы: 1) зная движение точки, то есть ур-ия движения (2), определить действующую силу, то есть функциональную зависимость величины и направления силы от времени ί, и 2) зная силу, то есть значения величин (108) как ф-ии времени, определить движения точки, то есть ур-ия движения (2). Масса точки в обоих случаях предполагается известной. Для решения первой проблемы очевидно достаточно взять вторые производные по ί от функции (2) и умножить эти производные на ш, что и определит X, Y, Ζ в функции t. Величина и направление F в зависимости от ί определяются уже затем равенствами (109) и (НО). Для решения второй проблемы, обратной первой, необходимо очевидно проинтегрировать систему трех диференциальных ур-ий 2-го порядка (108), вследствие чего х, у, ζ окажутся зависимыми не только от ί, но и от шести произвольных постоянных интеграции С, С₂, ., С₆, так что:

* ⁼ ., С₆); у—fz(l,С_Х,С₂,., С_е);

«=/|(“,ад, .,с₆),

или

r=r(t,C₁,C₂,.,C₆). (Ill)

Произвольные постоянные С_х, С₂, ., С₆ принимают однако вполне конкретные значения, если известны условия д в и ж ен и я точки в какой-нибудь момент, то есть если известны положение, величина и направление скорости точки в определенный момент. В частности эти условия м. б. н а-чальными, то есть соответствующими моменту t=0. Так, если F=0, то есть если движение равномерно и прямолинейно, то из (106) имеем α= 0, и следовательно

V=Const=У₀ (112)

или

dr

dt

(112)

Интегрируя (112), получаем:

r=v₀t+C. (ИЗ)

Если, при t=0, г=г₀, то из (113) получаем: С=г₀, т. ч. вместо (113) имеем:

r=v₀t + r₀, (114)

что равносильно трем ур-иям:

х=(v₀)J + х₀

У=ОоУ + Уо I > (¹¹⁵)

«=ОоУ + г_й)

где («о)“, (у₀)_у и («₀)₂—проекции v_a на оси координат, а х₀, у₀, г₀—координаты начального положения точки определяемого радиусом-вектором г₀. Ур-ия (115) и представляют собой ур-ия движения точки, содержащие шесть постоянных (ν₀)_χ, (v₀)_y, (v₀)_z, х₀, у₀, z₀. Ур-ия прямолинейной траектории точки получим, исключив ί из (115):

х-х₀_у-у₀ Ζ-Ζ о (®о)х (^vo)y (^vo) г

Пусть материальная точка, находящаяся под действием силы F и имеющая в данный момент скорость v, движется по траектории MN (фигура 40). Разложим F на две компоненты: одну F_t, называемую тангенциальной компонентой— по направлению касательной, проведенной к траектории в рассматриваемом положении точки, и другую, F_n, называемую нормальной компонентой,—по направлению соответствующей главной нормали кривой MN. Из (106), (44) и (45) имеем тогда:

F_t=(ma=ma_t=±m^dd (117)

F_n=(та)_п=та_п=т _ρ ρι, (118) причем модули этих компонент:

(U7)

F_n=m^v (118)

а модуль силы:

*-^т/ТтУ + {тУ· ^

Так как вектор полного ускорения а лежит всегда в соприкасающейся плоскости кривой и направлен всегда внутрь кривизны кривой, то, как это видно из (106), и вектор F лежит в соприкасающейся плоскости и также всегда направлен внутрь кривизны траектории. Отсюда также следует, что компонента силы F по бинормали всегда равна нулю. Как видно из (117), тангенциальная компонента F_t влияет лишь на изменение линейной скорости v, то есть обусловливает изменение равномерности движения точки; нормальная же компонента, как видно из (118), влияет на радиус кривизны траекто рии, то есть обусловливает отклонение движения точки от прямолинейности. Т. о., если F_t= 0, то есть если сила F в любом положении точки направлена по главной нормали, то точка движется равномерно; в самом деле, в этом случае имеем из (117):

~=0 и v=Const.

dt

Если же в любом положении точки F_n=0, то точка движется прямолинейно; в самом деле, в этом случае имеем на основании

(118)=0 и ρ=οο, что указывает на пря молинейность траектории. При круговом движении точки имеем на основании (44"), (45") и (46):

Е_г=±тД~= ± Й0, (117")

F_n=mRcо², (118")

F=mR j/θ² + ω“, (119)

где R—попрежнему радиус окружности, по которой движется точка. Если точка движется при этом равномерно, и так как в этом случае F_t=0, то

F ^ F_n=mRoA, (119")

так что сила F в равномерном движении по кругу все время будет направлена к центру окружности. Эта последняя сила представляет собой частный случай т. н. центральных сил, таких сил, линии действия которых проходят через одну и ту же точку. Пусть F представляет собою некоторую центральную силу, проходящую через точку О. Далее, так как направление а всегда совпадает с направлением F, то линия действия а также все время проходит через О, так что точка будет совершать центральное движение, то есть, как это видно из равенства (54), сектори-альная скорость движения точки постоянна, а радиусвектор, определяющий положение движущейся точки и имеющий начало в О, ометает площади, пропорциональные фигура 41. истекшим промежуткам времени. Такого рода движения совершают например планеты,находящиеся под действием силы притяжения солнца (законы Кеплера).

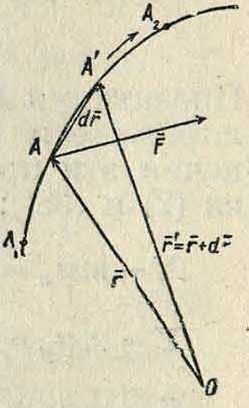
Пусть точка, находящаяся под действием силы F, переместилась за бесконечно малый промежуток времени dt из положения А, определяемого радиусом-вектором г, в бесконечно близкое положение А (фигура 41), определяемое вектором г=г -f dr.

Элементарной работой dT силы F называется скалярное произведение векторов F и dr, так что

dT=F dr=F dr cos (F, dr), (120) причем dr M. б. отождествлен с элементом ds пройденного пути. В зависимости от того, будет ли A- (F, dr) > или <90°, и элементарная работа dT будет либо положительна либо отрицательна. В последнем случае F называется тормозящей силой. Если же -4 (F, dr)=90°, то есть если F

нормальна к траектории, то и<2Т=0. Если модули проекций dr на оси координат обозначив через dx, dy, dz, то, пользуясь ф-лой векторного исчисления AH — A_xh_x-{-А_уВ_у- -+ A_ZB_Z, имеем из (120):

dT =×dx + Y dy + Z dz. (121)

Пусть, далее, за промежуток времени от до t₂, равный Δί, точка переместилась из положения А_г в положение А₂. Полной работой Т силы F за этот промен-суток времени на этом пути называется сумма всех элементарных работ за этот же промежуток на этом же пути, то есть

А₂ -А 2

Т=j Fdr=j F cos F,dr)dr =

А₁ А_г

A₂

= J (Xdx+Ydy +Zdz). (122)

-Д i

В частности, если точка движется прямолинейно и если F совпадает с направлением движения, и так как в этом случае 6oiilF, г)=1, то из (122) имеем: а₂

Т=f Fdr. (1220

4-1

Если к тому же F=Const, то имеем из последнего равенства:

T=Fs, (122-0

где s=r₂—r_l—путь, пройденный точкой за рассматриваемый промежуток времени. Если же в любом положении точки F нормальна к траектории, т. e. F J_ dr, и т. к. в этом случае cos (F, dr)=0, то из (122) имеем Т=0. Если на точку действует ряд сил F_lt F₂, F₃.

F_n, причем равнодей ствующая их F=F_x -f F₂ +. + F_n, то из (122) имеем:

А-2

Т=j F dr=J (F₁ -f F₂ +. + F_n) dr =

a₂

= J F_± dr

Аг где Т_1г T.

Jf₂ dr +.=т₁+т₂ + .+т_п

2>

Ai

t₃.

.,T_n—полные работы сил составляющих. Следовательно полная работ а равнодействующей силыбудет равна ал-гебраич :ской сумме работ сил составляющих. Если вообще работа силы за промежуток Δί равняется ΔΤ, то средне! мощностью работы W_cp. за рассматриваемый промежуток времени называется

Δ7

частное -гг, так что м

W =

ΔΤ Δί ‘

(123)

Истинною же мощностью W в данный момент называется предел частного (123) ;при Δί->0, так что

W=^lim (—)=—. (124)

^ГГ Δί—>0 Δί dt ⁽ >

Из равенств (120), (106), (37) и (15) имеем .далее: dT=F d/r =

i dr=m drj=m (dv v) —

= d Q τηνή=d(l ηινή=dL. (125)

Выражение L=| mv~ называется живою силою, или кинетической энергией точки. Т. о. по (125) имеем, что элементарная работа силы F равняется дифе-ренциалу живой силы точки. Если в положении А_х линейная скорость точки равнялась v_u а в положении А₂ равнялась v₂, то из (122) и (125) имеем:

!-ψ, (1250

Αχ

то есть полная работа силы за какой-нибудь промежуток времени равняется изменению кинетич. энергии точки за тот же промежуток времени, причем это изменение м. б. как положительно, так и отрицат“ льно, в соответствии с чем и работа будет либо положительной либо отрицательной.

Понятия работы, мощности и живой силы принадлежат к т. наз. производным понятиям динамики. К числу последних принадлежат также и понятия количество движения и импульс силы. Количеством движения точки называется произвед< ние массы m точки на скорость v последи“ й. Обозначая количество движения через К, имеем следовательно: K=mv. (126)

Очевидно вектор К в m раз больше вектора v и совпала¹ т по направлению с последним. Вектор F dt называется элементарным импульсом силы, а вектор Fidt, где F_t есть компонента F по некоторому направл нию I, называется элементарным импульсом силы по направлению I. Полным импульсом силы J за промежуток времени от t_x до ί₂ называется сумма всех элеме нтарных импульсов силы за рассматриваемый промежуток времени, то есть б

J=Г F dt. (127)

h

Аналогично этому имеем полный импульс силы по направлению I:

*2

t/j=Jf dt. (127)

tl

Так как F =×+ ΐ + Ζ, то из (127) имеем: *2

-r=J(X + r +Z)dt =

tz t2 ^2

=jT Xdt +J‘r dt + J Z dt=J_x + J_y + J_z,

t1 tl tl

г. e. полный импульс силы равен сумме полных импульсов силы по осям координат. Из (127) непосредственно следует, чίο

%=(128)

то есть производная по времени от полного импульса силы равняется действующей в данный момент силе F. Из (127) имеем также, принимая во внимание (106) и (37): б *2

J=jmadt=mj dv=mv₂ — mv_lt (129) б б где ь и г>_а — скорости точки в моменты и <₂. Т. о. видно, что полный импульс силы за какой-нибудь промежуток времени равен изменению количества движения за тот же промежуток времени.

Рассмотрим теперь такую силу F, величина и направление которой зависят только от положения точки приложения силы, так что F=F(x, у, z), (130)

или, что равносильно:

Х=Х(х, у, z) 1 У=У (ж, у, z) · (130)

Z — Z (х, у, z) j

Если последние ф-ии однозначны и непрерывны в определенной области, то каждой точке области соответствует сила определенной величины и определенного направления. Совокупность всех таких точек составляет т. н. силовое поле, или поле сил. Допустим кроме того, что имеется такая однозначная непрерывная ф-ия U(х, у, z), которая обладает следующими свойствами:

<Ю_ дх ВЦ ду

ЗС7 _ „

02 ^Z

= -Х=— У

(131)

Если такая ф-ия U для данной силы (130) существует, то она называется по отношению к данной силе силовой, или п о-тенциальной, а сама сила называется потенциальной. Нетрудно видеть, что если данная сила потенциальна, то т. к. из (131) имеем:

ах aw 9Y aw

dy

TO

и аналогично:

aw	dY
дуах	И — дх
ах	_0У
ау	дх
0У	_ az
dz	~ ду
az	_ дх
дх	= 02,

дхду’

(132)

Последние равенства и представляют собой условия, необходимые и достаточные для того, чтобы данная сила F была потенциальной. В последнем случае имеем на основании равенства (131):

F-Xi+YJ + Zk-^gi~§j-§*-

= — yU=— grad U, (133)

так йто F—градиент функции U (смотрите Векторное исчисление). Так как функция U однозначна, то каждой точке рассматриваемого силового поля соответствует одно, и только одно, значение функции U, получаемое подстановкой в U (х, у, z) координат данной точки х_и у_и z₍ вместо текущих координат х, у, z. Полученное т. о. значение U называется потенциалом поля в рассматриваемой точке. Пусть точка переместилась под действием потенциальной силы F из положения А, определяемого радиусом-вектором г, в бесконечно близкое положение. Элементарная работа силы F при этом перемещении будет по (121) и (131): dT =×dx + У dy + Z dz =

(§£**+%- dy + g dz). (133)

Допустим далее, что пцд действием данной потенциальной силы F точка nepi мести-лась из положения .(,Γι, y_lt z_x) в положение А₂(.г₂, у_г, г₂) по некоторой траектории А_ХСА₂ (фигура 42). Пусть потенциалы поля в этих точках будут соотв тственно Ui — U(x_lt у_1г ζ_χ), U₂=U(x₂, у₂, z₂). Тогда полная работа силы F при рассматриваемом перемещении точки будет равна на основании (122) и (131):

Д 2

Т=J (X dx + У dy + Z dz) =

A-i.

^2

dU dz

S (%*>+%**+%*)-

-J du~u_x-

U,

(134).

так что полная работа Т равняется разности потенциалов U₁ — U₂. Отсюда видно, что работа Т ποτι нци-альной силы F не зависит от самой траектории А_ХСА₂, а только от положения крайних точек ее. Это свойство называют свойством консервативности потенциальной силы. На этом основании нетрудно прийти к выводу, что работа потенциальной силы по всякому замкнутому контуру А₁СА₂СА₁ равняется 0: Сравнивая равенства (125) и (134), имеем также:

или

mvS rrvi _{тг ττ}X----2~- Uj-Uj,

ψ + υ^ψ+υ,

(135)

(135)

так что для всех точек поля

+ Uj= Const. (136)

rrv²,

Живая сила - ₂ - характеризует кинетическую энергию материальной точки массы m в положении (x_it y_h z₍), а потенциал U_i—п о т е п ц и а л ь н у ю энергию материальной точки в том лее ее положении. Т. о. ур-ие (136) выражает, что сумма кинетич. и потищиальчой энергии материальной точки, переме щающейея под действием потенциальной силы, есть величина постоянная для данного силового поля. Совокупность всех точ. к поля, имеющих один и тот же потенциал, представляет собою в виду однозначности и не прерывности функции U очевидно некоторую поверхность называемую эквипотенциальной, или поверхностью уровня. Уравнение эквипотенциальной поверхности очевидно будет:

U(x,y,z)~C, (137)

или

dU=0, (137)

где С—нек-рая произвольная постоянная. Меняя значение постоянной С, получим целое семейство эквипотенциальных поверхностей. Проведем из какой-либо точки О (фигура 43) поверхности уровня U(x, у, z)= С нормаль п к последней и пусть эта нормаль образует с осями координат углы а, β, γ. Тогда имеем на основании выводов дифе-рвнциальной геометрии (смотрите):

cos α=

cos β =

cosy =

	дх
/©+(£) dU bу			2+	dUf dz )
/(1Г+® 6U dz			3+	dUy dz )
		(am ду	2+

(138)

Пусть, с другой стороны, линия действия силы F, действующей в точке О, образует СчОсями координат углы а, β, у. Из равенств (109), (110) и (138) имеем:

, X

cos α= — .— =

γ/Χ*+Υ*+Ζ²

au

дх

= cos а и аналогично:

cos β=cos β, cos у=cos γ.

Τ. о. потенциальная сила F направлена по нормали к поверхности уровня, проходящей через точку приложения F. Это же можно усмотреть и непосредственно из формулы (133), исходя из самого понятия градиента функции U. Так как по определению все точки поверхности уровня имеют один и тот же потенциал, то из (134) имеем: 1) полная работа потенциальной силы при перем! пгнни точки по поверхности уровня равнж тся нулю и 2) работа потенциальной силы по произвольному незамкнутому контуру, имеющему крайние точки на одной и той же поверхности уровня, равна 0.

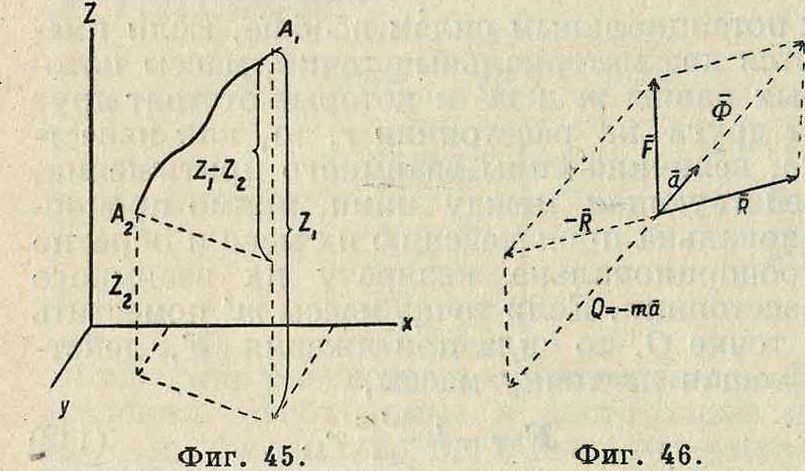
Нетрудно видеть, что всякая центральная сила есть сила потенциальная. В самом деле: допустим, что имеется некоторая центральная сила F, линия действия которой проходит через центр О и величина которой F зависит от расстояния АО=г, где А— точка приложения силы F (фигура 44), так что Н=/(г).

Если —единичный вектор, определяющий направление ОА, то вследствие центральности силы F имеем:

F=± Kr_x=± f(r)r_x, (139)

причем знак (+) соответствует случаю о т-талкивающей от О силы, а знак (—) соответствует случаю притягивающей к О силы. Элементарная работа силы F равняется, на основании (120) и (139): dT — F dr=± f{r) (ту dr) =

= ± f(r)dr (r_x- r_x) ± f{r) r(r_x dr_x) =

= rt f(r)dr, (140)

τ. к. (r_x · r·)=1, a (r_x dr_x)=0, ибо r_x J. dr₁. Обозначая

F f /(r) dr + C=U, (141)

имеем из (140):

dT=— dU, или T=U₁—U_i, что и доказывает свойство консервативности всякой центральной силы, а вместе с тем н то, что она потенциальна. Ур-ие поверхности уровня будет по (137):

<Ш=0,

или

/(г) dr=0; dr=©; г=Const, то есть поверхности уровня представляют концентрические шаровые поверхности, центр которых совпадает с центром О. В частности сила взаимного тяготения, д“ йствую-щая по закону Ньютона как сила центральная, есть в то же время и сила потенциальная, так что по отношению к ней применимы все выводы, сделанные выше по отношению

к потенциальным силам вообще. Если имеются две материальные точки, массы которых равны т и т и которые отстоят друг от друга на расстоянии г, то, как известно, величина силы взаимного притяжения, действующая между ними, прямо пропорциональна произведению их масс и образно пропорциональна квадрату их взаимного расстояния. Если точку массы т поместить в точке О, то сила притяжения F, действующая на точку массы,

(142)

где к—некоторый универсальный фактор пропорциональности. Обозначая кт через μ², имеем также

₇ тт

^=-к-^г_х

F-

1&т

_r2 -X. (142)

Сравнивая равенства (142) и (139) и принимая во внимание, что в данном случае F есть сила притяжения, имеем:

№-*£· (143)

так что по (141):

U-fegdr-pm + (144)

Если при г=г₀ потенциальная ф-ия U имеет значение U₀, то из (144) имеем:

Uq => — --- + С, или С

Го тт i Д²т ^U°+ г₀

так что

U (144)

Нетрудно видеть, что сила тяжести Р=тд есть также сила потенциальная. В самом деле, если оси координат Ох и Оу взять в горизонтальной плоскости, а положительное направление оси Oz взять вертикально вверх, то

Х=0; Г=0; Z=— тд. (145) Так как условия (132) при этом удовлетворяются, то сила Р потенциальна. Для того чтобы найти соответствующую потенциальную функцию, имеем из (133), принимая во внимание (145),

— dU=Xdx+Ydy+Zdz=—mgdz, (146) откуда интегрируя получаем:

U=+ т gz + С. (147)

Если точке, имеющей ординату z=z₀, соответствует потенциал U₀, то из (147) находим:

С=U₀ — mgz₀,

так что

U=тд (z — z₀) + U₀. (147)

Ур-ие поверхности уровня U=Const дает в данном случае: z=Const. Т. о. поверхности уровня представляют собой в рассматриваемом случае горизонтальные плоскости. Пусть точка nepeMi стилась из положения A_lt где потенциал И±, в положение AJ, где потенциал (фигура 45). Полная ра бота силы тяжести Р при этом перемещении по (134) и (147):

Т=U₁ - U₂=[mffCsi - z₀) + U„] --[mg(z_i-z₀)+U₀]=mg(z₁-z₂)=P(z_i-z₂), (148)

где z_x и г₂ представляют собой координаты соответствующих положений точки. Т. о.

работа силы тяжести при всяком перемещении весомой точки равняется произведению величины силы Р на разность высот положений точки. Очевидно, если точка nepeMi щается в горизонтальной плоскости, то, так как разность высот равна нулю, работа силы тяж сти также равняется нулю.

До сих нор мы рассматривали движения лишь т. н. свободных точ ж, то есть точек, подвергавшихся воздействию только нек-рых сил, из которых каждая стремилась сообщить точке определенное движение. Но имеются случаи, когда па движение данной материальной точки помимо данных сил влияют еще и другие причины, как например воздействие данной поверхности или кривой, по которым материальная точка вынуждена пер< мещаться (тело, перемещающееся по данной поверхности, шарик, перемещающийся внутри трубочки и т. и.). В поел д-HtM случае точка называется несвобод-н ой или находящейся под действием свя зей. Очвидно представляется возможным найти такую силу, действие которой могло бы заменить действие данной связи; такая сила называется реакцией, или силой, связи. Прибавив реакцию R данной связи к данным силам, прилож, иным к точке и имеющим равнод( йствующую F, можно будет опять рассматривать точку как свободную, к которой приложены силы f и R, так что ур-ие движения точки будет по (107):

m^=F + R. (149)

Равнодействующая Ф=F + R называется эффективною силою в отличие от F, называемой силою движущей. Если реакция связи R не дана, то оч видно, что ур-ия (149) недостаточно для определения движения точки, т. к. содержит в сущности три неизвестных компонента силы R по осям координат, вследствие чего явлж тся необходимым получить три новых ур-ия. Если точка вынужд! на перемещаться по некоторой поверхности S, то ур-ие этой поверхности fix, у, z)=0. (150)

и представляет собою одно из необходимых дополнительных ур-ий. Если же точка вынуждена пер( мпцаться по некоторой кривой С, то ур-ия этой кривой

А(ж, У, «)=0 h(x, y,z)=0 f

(151)

представляют собой два из необходимых дополнительных ур-ий. Три ур-ия

А(ж, У,г)=0 ]

№.V,z)-0} (152)

/₃(ж, у, е)=0 )

дают только одно определенное положение точки, так что перем( щение последней ока-зыва(тся невозможным. Если связи абсолютно гладкие, то есть (ели реакция связ< и не имеет таны нциальных компонент, то R нормальна как к поверхности S, так и к кривой С. Принимая это обстояы льство во внимание, получа! м два уравнения, выражающих перш ндикулярностьВ к поверхности S, и одно ур-ие, выражают е перпендикулярность R к кривой С. И в том и в другом случае мы следовательно получаем по три добавочных ур-ия, необходимых как для полного определения двшк ния точки, так и для нахождения неизв стных компонент реакции связи R. Распространяя этот вывод и на крайние случаи абсолютно свободной и абсолютно hi свободной точек, можно сказать, что в первом случае эти три добавочных уравнения дают условие R=0, а во втором—условие v=0. При наличии поверхности S можно две из п. рем! н-ных в личин х, у, z выбрать произвольно, а третью опред( лить через первые две из уравнения (150). Произвольно взятые координаты называются свободными (смотрите Координаты). При наличии же кривой С можно произвольно взять только одну из тр^пх координат, а оставшиеся две определяются через первую из ур-ий (151). Так как в п рвом случае точка обладав т болыш ю свободою движения, ч. м во втором, то число свободных координат принимается как величина, определяющая степень сво-

боды точки, находящейся под действием связей. Точка следовательно имеет 3, 2, 1 и 0 стелет и свободы в зависимости от того, перемещается ли она свободно по поверхности, по кривой или совершенно неподвижна. Ур-ие движения (149) м. б. представлено еще и в следующем виде:

JF· + JR+ (-та)=0, (153)

что м. б. интерпретировано след. обр. Допустим, что кроме сил F и И к точке приложена еще одна сила

Q=— та. (154)

Тогда, как это видно из (153), все три силы взаимно уравновешиваются. Эта фиктивная по отношению к движущейся точке сила Q называется силою инерции. Т. о. получается, что данная материальная точка, находящаяся под де йствием сил F и R, движется так, что в каждый момент движения силы F, И и сила инерции взаимно уравновешиваются. В этом собственно и заключается т. наз. принцип, или начало, Д’Аламбера. Равнодействующая сил F .Hj^ypaBHan — M, называется потерян-н о ю с и л о ю (фигура 4G). Оч видно также, что сила инерции Q по величине своей равна эффективной силе Ф, но по направлению противоположна последней, так что Q= — Ф. При всей своей простоте принцип Д ’Алам-бера во многих случаях значительно облегчает исследование законов движения точки, сводя вопрос о движении точки к вопросу о ее равновесии.

Допустим, что материальная точка вынуждена перемещаться понеко орой кривой С. Спроектируем силы F, И и Q на направления: касательной к кривой, проведенной в сторону движе ния точки, главной нормали, проведенной к центру кривизны кривой в рассматриваемом положении точки, и бинормали (фигура 47). Так как В нормальна к кривой, то есть Β± τ_χ, где τ₁ ποπρι жне-му единичный вектор, определяющий направление касательной, то, обозначая компоненту F по касательной через F_t, имеем из (117) и (149):

F_t-m^ τ,-0. (155)

Обозначая компоненты F и В по главной нормали через F_n и В_п, имеем из (118) и (149):

F_n + В_п — ^п~ о_г=0. (156)

Компонента силы инерции Q по главной нормали

^ την² --

ft» - - — Qi

(156)

называется центробежной силой инерции. Если точка движется по окружности с угловой скоростью со, то, так как ν=ωτ и ρ=7·, имеем:

О_и=-тсо²ге₁ (156")

При равномерном круговом движении Q=Qn-

Т. к. далее по (47) проекция полного ускорения а на бинормаль равна 0, то из (153) имеем также гд° F_b и В_ь суть компоненты сил F и В по бинормали. В виду того, что В при абсолютно гладких связях всегда нормальна к траектории точки, находящейся под действием этих связей, то полная работа В при любом перемещении точки равняется нулю, что справедливо и для вышеуказанных крайних случаев (_β=0 или г>=0). Таким образом

f В dr=0. (158)

Допустим, что точка, находящаяся под действием связи, представляемой поверхностью S, начала перемещаться из состояния покоя под действием сил F и В. Это движение в начальный момент происходит по направлению равнодействующей их, то есть по направлению эффективной силы Ф. Очевидно, что элементарная работа обеих сил в этот момент положительна, так что

(F + В) dr > О

и так как то

Bdr=О, F dr > О,

(158)

т. e. F dr cos {F, dr) > 0 или cos (F, dr) > 0.

Отсюда видно, что начальное элементарное перемещение dr образует с силою F острый угол. Если сила F потенциальна, то так как по (133) dT=F-dr=— dU, то следовательно в рассматриваемый момент

dU < 0, (159)

то есть, другими словами, при начале движения потенциал U должен убывать. Отсюда Следует, что если среди всех возможных элементарных перемещений, допускаемых данной связью, нет ни одного, при к-ром бы потенциал U убывал, то точка под действием сил F и В не может прийти в движение и следовательно будет находиться в равновесии. Та- Фигура 47. кой случай может представиться например, если точка находится на поверхности S в таком положении, при ш> тором U принимает максимальное или минимальное значения, так как в этом случае при всех возможных элементарных перемещениях, допускаемых связью, dU=0. В случае, если в качество силы ^является вес материальной точки В=тд, то так как в этом случае по (146)

dU=mg dz

и так как в начале движения dU < 0, то в этот же момент

dz < 0,

то есть весомая точка начинает двигаться под действием сил Р и В так, что z убывает, то есть начинает двигаться вниз. Т. к. работа силы В при движении точки равняется нулю, то ур-ия (125) и (125) применимы и для несвободной точки, рассматриваемой как точка, к которой как будто бы никакие реакции связей не приложены. Если же сила

F потенциальна, то и ур-ие (135) м. б. применено при таком же игнорировании силы И. Отсюда между прочим следует, что если имеем ряд материальных точек, падающих под действием силы тяжести в пустоте с одной и той же высоты, причем одни из них свободны, а другие вынуждены перемещаться по гладким поверхностям или кривым, то, находясь на одной и той же высоте, все они имеют одну и ту же скорость. Пусть нек-рая материальная точка вынуждена перемещаться по гладкой кривой С. Так как по (158)

JB|· dr=О,

то, умножая скалярно левую часть ур-ия (153) на dr, получаем:

F dr- та -dr=0. (160)

Допустим, что рассматриваемая точка находится в покое. Тогда имеем из (1С0),так как α= 0:

F dr=0, (161)

т. e. F±dr. Т. о. для того, чтобы точка, находящаяся под воздействием связи С, была в равновесии, достаточно, чтобы движущая сила F была нормальна к кривой С. Если же точка перемещается по кривой С, причем F=0, то из (155) имеем

do _ _п

= 0,

и следовательно v=Const, так что в рассматриваемом случае точка перемещается по кривой с постоянною линейною скоростью v. Из (157) и (156) имеем также в этом случае

£ г О	(162)
rra>2 -®»--6ι.	(163)
что
	(164)

Выводы, касающиеся движения точки по данной кривой или по данной поверхности, имеют большое прикладное значение, как например при исследовании движения маятника и во многих других случаях (смотрите Маятник, Колебательные движения).

До сих пор мы рассматривали связи, не Зависящие от времени ί, то есть не изменяю-щ» ся с течением времени. Однако может случиться, что во время перемещения точки по данной связи сама связь также изменяется, что имеет например место, если точка перемещается по кривой или же по поверхности, которые в свою очередь перемещаются в пространстве. В последнем случае уравнения (151) кривой С или уравнение (150) поверхности S содержат в явной форме помимо переменных х, у, z такж > и переменную t. Для определения движения материальной точки, находящейся под действием силы F при наличии связи, зависящей от ί, можно поступать точно таким же образом, как и выше, то есть исходить из содержащихся в (149) трех основных координатных ур-ий динамики в соединении с тремя ур-иями, выражающими данную связь и перпендикулярность ее реакции. Но в дальш йшем выводы о движении точки при наличии связи,

не зависящей от времени, к рассматриваемому случаю неприменимы. В то время как в первом случае, например траектория, описьп ваемая точкою в пространстве, вполне совпадает со связью, осуществляемой кривою С, во втором траектория точки отличается от кривой С; вследствие этого сила R перпендикулярна к траектории при связи, не зависящей от времени, и не перпендикулярна к траектории при связи, зависящей от t. Если точка вынуждена перемещаться по прямой, в свою очередь вращающейся около одной из своих точек, то очевидно, что траектория точки есть некоторая кривая, и что перпендикулярная к прямой сила It не будет перпендикулярна к траектории точки.

Выше при установлении уравнения (153) мы видели, что законы движения точки м. б. сведены к законам равновесия точки, находящейся под действием определенных сил, и что это обстоятельство упрощает в значительной степени исследование законов движения. Этот метод оказывается еще в большей мере полезным при исследовании движения системы материальных точек. Поэтому целесообразно сначала установить общие законы статики точки и твердого тела, а затем перейти к исследованию законов движения системы точек и в частности— твердого тела.

Статика. Допустим, что к какому-нибудь твердому телу приложена система сил JF_lt

F₂.F_n, величины, направления и линии действия которых известны. Основной задачей статики является определение условий, при которых данные силы взаимно уравновешиваются или, если данные силы не уравновешиваются, то каковы должен быть те силы, которые необходимо прибавить, чтобы равновесие имело место. При этом нужно различать следующие системы сил: 1) сходящуюся систему сил, то есть такую систему сил, линии действия кот, рых пересекаются в одной точке, в отличие от п е с ходя-ще и с я системы сил, линии действия которых в одной точке не пересекаются; 2) плоскую систему сил, то есть систему сил, линии действия которых лежат в одной плоскости, в отличие от неплоской системы, у которой линии действия сил в одной плоскости не лежат. В основе всех выводов статики лежит следующий принцип: для того чтобы две силы f и jF₂, приложенные к одному и тому же телу, взаимно уравновешивались, необходимо и достаточно, чтобы силы были равны по величине, противоположны по направлению и чтобы линии действия их совпадали (3-й закон Ньютона); при этом расстояние между точками приложения сил никакой роли не играет. Отсюда следует, что все силы, имеющие одну и ту же величину, общую линию действия и направленные в одну и ту же сторону,—э к вива-лентны, Вследствие этого вектор силы в статике принадлежит к категории так паз. скользящих векторов. Отсюда также следует, что для полного определения силы необходимо знать не только ее величину и направление, но и линию действия ее.

Пусть к данному телу приложена сходящаяся система сил J?!, F_t,., F_n, линии дей-

ствия которых пересекаются в точке О. Переместив все силы по линиям их действия так, чтобы точкй приложения их совпали с точкою О, получим новую систему сил Fi, Fi, ., F_n, эквивалентную данной. Заменив последнюю систему сил их равнодействующей F, по вышеприведенному способу, то есть построив на этих силах силовой мн-к и проведя замыкающую сторону от точки О к концу силового мн-ка, получим также и равнодействующую для данной системы сил. Очевидно, что если прибавить к данной системе сил силу — F, то вся совокупность сил уравновесится; поэтому сила —F называется уравновешивающей.

Пусть к данному телу приложена плоская несходящаяся система сил F_X,F₂, F_n, линии действия которых суть 1_Х, 1₂, ., 1_п. Продолжив линии действия I _х и 1₂ до их взаимного пересечения в точке О _х и сместив F_x и F_t в эту точку, заменим их одной равнодействующей F_X2=F_X+F₂. Продолжив затем линию действия 1₁₂ силы до пересечения с прямой 1₃ в точке 0₂, заменим аналогичным способом силы F_la и F₃ одною равнодействующей F₁₃ и т. д. Т. о. всю данную плоскую несходящуюся систему сил можно в общем привести к одной равнодействующей силе F. Однако, если в процессе, последовательного сло- f₂ жения сил встретятся -Кд· параллельные силы, то fJM приведенный метод оче-g*^o видно неприменим, ибо ^{2 2} соответствующие им ли нии действия не дают точки пересечения^ находящейся наконечном Фигура 48. расстоянии. В этомлглу-

чае сложение сил м. б. произведено след, образом. Допустим, что к двум различным точкам тела А_х и А₂(фигура 48) приложены две силы F_x и F₂, параллельные и направленные в одну и ту же сторону,причем пустьF_x=A_xB_x-hF₂=A₂B₂. Соединив точки А_х и А₂ прямою А_ХА₂, при--> —:—>

ложим к ним 2 силы F{=А _ХС _х и Fi=А ₂С₂, равные по величине, противоположные по направлению и линии действия которых совпадают с А_гА₂. Очевидно, что система сил F_lt F₂, Fi, Fi эквивалентна совокупности первоначальных двух сил. Заменив силы

F_x и Fi их равнодействующей Qi= A_XD_X== F_x+Fj, а силы F₂ и F₂ равнодействующей Q₃= А ₂£>₂=F₂ + F₂, получим новую систему сил Q_x и Q₂, эквивалентную первоначальной. Т. к. Q_x и Q₂ уже не параллельны, то, продолжив линии действия их до пересечения их в точке О и сместив силы

QihQjB точку О, так что 0Е_Х=Q_x и СЕ ,==Q₂, получим равнодействующую силу F —

— ОЕ=ОЕi+OE₂ как для системы Q_x, Q₃, так равно и для данной системы сил F_X,F₂. Проведя далее из точек Е_х и Е₂ прямые В_хК_хпЕ₂К₂, параллельные А_хА_г, имеем:

= ^А0.

Ж^д два равенства,

Δ0Ε_χΙС_х=Δ A_xD_xB_x и АОЕ₂К₂=Δ A₂D₂B₂, так что ОК_х=F_x и ОК₂=F₃. С другой стороны, так как Δ ΟΕ_ιΚ₁=Δ ЕК₂Е₂, то 0К_Х= =К₂Е и Е_хК_х=Е₂К₂. Таким образом имеем: F=ОЕ=ОК₂ + ЩЁ=ОК₂ + 0К_Х=Ft + F_a, то есть что величина (т. нэз. модуль) равнодействующей силы равняется сумме величин сил составляющих. Так как OE F_x F₂, то имеем также F=F_x + F₂. Продолжив ОЕ до пересечения с А_ХА₂ в точке А, имеем далее: Δ АА_хО <s> Δ К_хЕ_хО и Δ АА₂0 <*> Δ К₂Е₂0, так что

ΑΑχ __ АО ^ ЛЛ₂Κχδ ь₂к.

Деля почленно последние имеем:

АА_Х дДО eJo аа₂ ΕχΚ_χ Що ’

или, принимая во внимание, что Е_ХК_Х=Т₂К₂, получаем:

аа_{х =} f₂АА₂ Fi

Т. о. линия действия равнодействующей F делит отрезок А_ХА₃ внутренним образом на части, обратно пропорциональные величинам сил F_x и F₂. Из (165) имеем далее:

АА_Х Ft АА_Х F₂

—(=7-==—, ИЛИ =4=~

AA_x + AA₂ Fi + Ft А_хА₂ F

Если повернуть силы F_x и F₂ около точек их приложения, сохраняя при этом их величины и параллельность, то т. к. при этом величины А_хА₂, F₂ и F, как видно из (166), не изменятся, не изменится и расстояние АА_Х, то есть линия действия системы повернутых сил будет также проходить через точку А, которая вследствие этого и называется центром данных параллельных сил. Если V_х, г₂ и г—радиусы-векторы, определяющие соответственно положения точек А_х, А₂ и А, то, так как эти точки лежат на одной прямой, имеем:

[О - г_х) {г₂ - г_х)]=О,

или, что равносильно:

5С-Ж, V-Vl z-z_x

(165)

(166)

(167)

. (167)

Х₂-.Х_Х y₂-V_X Zt-z! ⁴

где х_х, у_х, г_х и х₂, у₂, z₂—координаты точек А_х и А₂. Ур-ие (167) или (1670 представляют собой ур-ия прямой А_ХА₂. Если координаты центра А параллельных сил обозначить через х₀, у₀, z₀, то из (1670 и (166) имеем:

*ο-*ι _ Vo-Vi _ Zq z_x

*2-

χ_χ y₂-y_xΑΑ_Χ _ _F₂Fi

z₂-z_x

₌ F± F₂ F

Из последних равенств получаем: x₀F=x_xF_x + x₂F₂ 1 УоЕ=y_xF_x + y₂F₂ >. z₀F=z_xF_x + z₂F₂ j x_xF_x -{ x₂F₂

(168·)

(169)

У o =

F, Vi F,

+ F₃+ V*F₂

F_x + F₂z _XF i + z₂F₂F j + F₂

0

Последние равенства определяют положение центра данных двух параллельных сил в зависимости от координат их точек приложения и от их величин. Если имеем три параллельные силы F _х, F₂, F₃. то, рассматривая отдельные силы F_l и jF₂, имеем координаты центра их по (169):

_ я₁’~1 + х_гг·.

У 0=

У!- 1

У2-»2. _ ^Ζ1^χ1 + ^z2^r i

> ² 0 ~~

⁰ F_x+F₂ ’ F₁+F₂ ’ "О Fi + F₂

Рассматривая затем систему, состоящую из равнодействующей F= F_x + .F₂ и третьей силы Р₃, получаем координаты центра всей данной системы:

Хо F1-2 Н" хЛ _ .X 1F; X₂F₂ г х?F1

Fi + F% + Д’з ж₀=-

Fι-г -г Ft

и аналогично: Уо =

yiF_l + y,F₂+ysF₃F i + i^2 + F3 ZiFi + z >F-i -f- z₃F₃

(169”)

Обобщая этот вывод для случая и сил, имеем в общем:

ΣΡίχι

Σρ*

Уо ¹

Σρ^ι

Σρ₂·

(170)

В частности силами jF могут явиться силы веса-Р^ m,sr; Р₂=m₂gr; Р_п= т_пд системы материальных точек, массы которых— т_г, т₃, ., т_и. Тогда имеем из (170):

х₀= Уо~ 2о =

ςρ,χι	Σ У{Хi
sp·	Σ Vi
ϊρ*%·	Σ у>т
ΣΡζ	Σ·4
ΣΡ jZi	Σ VjZj
	Σ,Ηί (

(171)

что м. б. представлено одним векторным равенством

mr₀=y,m_ir_i, (171)

где т—масса всей системы точек. В этом случае центр параллельных сил называется центром тяжести, или центром

7

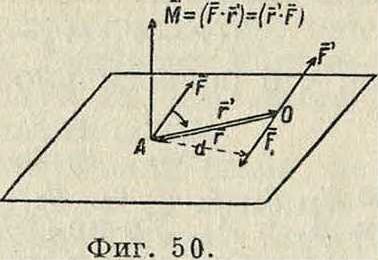
Фигура 49.

масс, системы материальных точек. Если система точек—твердое тело, то, обозначая вес элемента тела через dP=dm-g, имеем, суммируя (171) по всему объёму тела:

У о =

dP	x f dm · x
(V)	m
P	m
f dP	v dm у
(*>)	W
P	m
f dP	z fdm z
(»)

(172)

где Р и т—вес и масса всего тела (смотрите Масса). В рассмотренных выше случаях силы были параллельны и направлены в одну я ту же сторону.

Для того чтобы слозкить две силы Р, и Р₂ антинараллельные (фигура 49), то есть две силы параллельные, но направленные в противополозкные стороны, мозкно проще всего поступить след, образом. Пусть Р,>Р₂. Очевидно на основе вышесказанного можно силу _Fj представить как равнодействующую двух параллельных ей сил: F", приложенную к точке приложения А ₂ силы -F₂ “ равную по величине этой последней силе, и F{=Р_г — F[, приложенную к некоторой точке А. Тогда вместо системы сил F_x и F₃имеем систему Fi, F[ и F₂, а так как силы F; и .F₂ взаимно уничтозкаются, то остается одна лишь сила F, равная по величине Fj—F*₂ и приложенная к точке А, положение которой определяется след. обр. Из (166)

имеем:	Αχ A F _			(173)
	А,Аг Fi ’
ΛΛ ι	Fi	A Αχ	f2	(173)
А 2 Л.2 -f- -А Αχ	Fi + Fi	ААг	Fi

следовательно точка А делит отрезок А_гА внешним образом на части, обратно пропорциональные величинам данных сил. Из (173) имеем также:

AAj=А_гА_г рт=A_lA₂ ρ_ι _ р~

Из последнего равенства видно, что, чем больше F ₈ приближается по величине к F_ltтем дальше отодвигается точка А, и тем меньше становится Fi, так что в пределе при F!=F₂ получаем: AA_t= со и F=0. Таким образом две равные антипараллельные силы не имеют равнодействующей силы. Совокупность таких двух сил носит название пары сил (смотрите).

Из предыдущего ясно, что совокупность параллельных и антипараллельных сил можно привести к одной равнодействующей, величина которой равняется алгебраич. сумме величин сил составляющих, причем силы, направленные в одну сторону, берутся с одним знаком, а силы, направленные в другую сторону,—с противоположным знаком. При сохранении последи, правила формулы (170) определяют такзке положение центра рассматриваемой системы параллельных и антипараллельных сил. Если в частности Σ Р<= =0, то полозкение центра становится неопределенным; в этом случае вся система сил либо приводится к паре сил, либо силы взаимно уравновешиваются. Последний случай очевидно имеет место, если линия действия равнодействующей всех сил, направленных в одну сторону, совпадает с линией действия равнодействующей сил, направленных в противоположную сторону; первый зке случай имеет место, если эти линии действия не совпадают.

Пусть к точке А нек-рого тела приложена сила F (фигура 50). Возьмем на теле какую-нибудь другую точку О, положение которой по отношению к системе отсчета с началом вН определяется радиусом-вектором г.Приложим к О две силы F и F_x, первую параллельно, а вторую антипараллельно F, причем пусть F=F_X=F. Система сил F_x, F^r и F, эквивалентная силе F, м. б. рассматри-

ваема как состоящая из силы F и пары сил (F. F,). Т. о. силу F можно перенести, сохраняя ее величину и направление, в другую точку тела, прибавив при этом соответствующую пару сил. Момент пары сил, которую следует прибавить, равен (смотрите Пара сил):

M=[Fr], (174)

--->

или, если обозначить вектор О А через г== —г, то

М=[гЩ. (174)

Послелний вектор определяет также момент силы F относительно точки О. Если длина перпендикуляра, опущенного из О на линию действия силы F, равняется d, то получаем:

M=Fr sin (F, г)=Fd. (174")

Нетрудно видеть, что если О лежит на линии действия F, то т. к. в этом случае d=0, то и М=0; М=0. Пользуясь ф-лмми векторного исчисления, имеем из (174):

М_х=yZ — zY )

М_у=zX — xZ > (175)

М_г= xY—yX I

где х, у, г—координаты точки А по отношению к системе осей с началом в О, а X, Y, Z—модули компонент F по этим же осям. Векторы M_x=M_xi назы ваются моментами силы F по отношению к осям координат. В частности, если F лежит в плоскости ху, то т. к. 2=0 и Z — 0, имеем из (175):

М_х=0; М_у=0; M_z=xY-yX. Последнее равенство представляет собой также момент рассматриваемой силы F относительно начала О. Отсюда видно, что проекция момента какой-либо силы, взятого относительно некоторой точки, па какую-либо ось равняется моменту проекции силы на плоскость, перпендикулярную к оси, взятому по отношению к точке пересечения оси с плоскостью. Если к телу приложены п сил F_v F_t, ., F_n, то, взяв нателе произвольную точку О, можно к ней перенести все данные силы, сохраняя их величину и направление и прибавляя соответствующие этим переносам пары сил, моменты которых по (174) будут равны:

(г=1, 2.»), (176)

а модули моментов определяются равенствами (175). Все силы F_l, f_a, ., F_n, приведенные к точке О, м. б. затем заменены одной равнодействующей силой:

* - Σ*ί - 2 *<. ^(Ш)

1 1

а все пары—одною равнодействующей парою, момент которой (смотрите Пара сил)

Ж=2ж_г=2[П^]. (178)

i 1

Последний вектор называется главным моментным вектором системы сил по отношению к данной точке приведения сил. Т. о. всякую систему сил можно привести бесчисленным множеством способов к одной силе и одной паре сил. Очевидно для того, чтобы силы данной системы взаим но уравновешивались, необходимо и достаточно, чтобы как сила F, так и главный мо-ментный вектор М равнялись нулю, то есть чтобы

I?=2 *1=⁰ 1

η η

м=2^ж*⁼2[п“у=о

У (179)

что равносильно наличию шести ур-ий:

2*1-0; ^=0; (179)

1 1 1

Σ^^ζ*-**⁷ύ- 0; 2(г_гХ_г-®_г2_г)=°;

2 (ад У_г-г/_гХ_г)=0. (179")

i.

В частности, если система сил сходящаяся, то для равновесия системы необходимо и достаточно наличия только трех ур-ий (179), если система плоская—необходимо и достаточно наличия двух каких-либо уравнений (179) и соответствующего одного ур-ия из (179"); если же наконец система плоская и сходящаяся, то для равновесия системы необходимо и достаточно наличия только двух из ур-ий (179).

Допустим, что данная система сил, приведенная к точке О, дала равнодействующую силу F и равнодействующую пару момента М. Если мы возьмем затем другую точку приведения О, то равнодействующая F остается та же; изменится лишь главный мо-меятный вектор, превратившись в

М₀=М +М, (180)

где ЛГ—момент той пары, которую следует прибавить при перемещении F из О в О (фигура 51). Разложим момент М (фигура 52),

получившийся при приведении системы сил к точке О, на две составляющие: М_Л—по-направлению равнодействующей силы F и М_р—по перпендикулярному к F направлению. Проведя к плоскости (F, М) в точке О перпендикулярную прямую, можно очевидно найти на этой прямой такую точку Οχ, что при перенесении силы F и в О в О, нужно будет прибавить пару момента М== — М_р. Т. о. при приведении данной системы к точке Οχ и получаются сила F и три момента пар М_л, М_р и М, причем последние два момента взаимно уничтожаются, так что остаются только сила F и направленный по ней момент пары М_л. Отсюда видно, что всякую систему сил можно привести к одной силе и одной паре, момент которой совпадает с направлением силы (смотрите Винт в тео-ретич. механике). Из вышесказанного следует, что всякой точке тела при данной системе сил соответствует определенная пара векторов FkM при переходе от одной точки тела к другой меняется лишь вектор М, вектор же F один и тот же для всех точек тела. Нетрудно однако убедиться,что если провести какую-нибудь прямую· I, параллельную F, то моментный вектор для всех точек этой прямой будет один и тот же. В самом деле, пусть система сил, приведенная к точке О, не лежащей на Ϊ, дала векторы F и Μ. Т. к. расстояние d от О до I остается одно и то же, какую бы мы точку на прямой I ни взяли, то, как .видно из (174”), момент 31 силы F по отношению к любой точке О прямой I будет один и тот же, почему при приведении системы сил к любой точке прямой I придется к М прибавлять один и тот-же вектор 31, что и доказывает вышеприведенное предложение. Отсюда следует, что если провести плоскость S, перпендикулярную к F, то, исследовав характер изменений вектора М для всех точек этой плоскости, мы тем самым исследуем характер этих изменений для всех точек тела. Если точке Οι плоскости S(фигура 53) соответствуют векторы F и ЛС_гП F, то, перейдя к другой точке О той же плоскости, то есть перенеся силу F из Οχ в О, получим от этого переноса новый момент Ж _ перпендикулярный плоскости (1ί, ΟχΟ), причем М== F-OxO, и главный момент относительно О будет:

Ж=М_г + 31, (181)

или.

М²=Щ + М²=Ml + F² О^О² (181)

й :

Μι

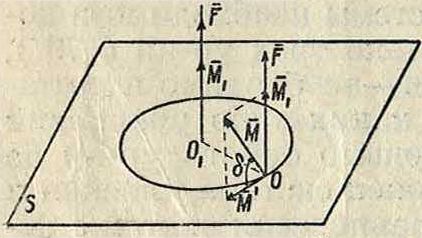
Фигура 53.

tgd =

М

(181”)

где б — угол между М и 31. Если провести в плоскости Я из О, радиусом 0,0 окружность, то так как М для всех точек окружности один и тот же, то и М для всех этих точек при данной системе сил есть величина постоянная, причем, как видно из (181) и (181”), с удалением О от О, величина М увеличивается, а вектор 31 все больше наклоняется к плоскости S. Если перейти к точкам в пространстве, то нетрудно усмотреть, что все точки, лежащие на круглой цилиндрической поверхности, ось которой преходит через точку О_х, перпендикулярно S, будут иметь одну и ту же величину М. Ось цилиндра, представляющая геометрия, место точек, по отношению к которым данная система сил приводится к совпадающим по направлению силе F и главному моменту Ж, называется центральной осью данной системы сил. Очевидно, что для точек центральной оси величина М достигает своего минимума. В частности, если в точке Οχ главный моментный вектор равен нулю, то система сил для всех точек тела приводится к одной силе F. Очевидно в этом случае

П П

М · F= 2-^afi-S-^Pi⁼⁰* ⁽¹⁸²)

или по (174)

[г, ЕЙ]· 2^=0. (182)

1 1

Если же F= 0, то положение центральной оси становится неопределенным, так как вся система сил приводится к паре, момент которой 31 свободен, то есть момент которой м. б. перемещаем параллельно самому себе в любую точку тела (смотрите Пара сил).

При выводе условий равновесия (179) мы полагали, что тело, к которому приложены данные силы Fx,F_it., F_n, свободно. Допустим однако, что тело находится под воздействием не только сил F_t, но и нек-рых связей. Очевидно, что, присовокупив силы реакции связей к данным силам F_t, мы можем тело вновь рассматривать как свободное, к к-рому следовательно применимы условия равновесия (179), с тем однако отличием, что в числе сил F_{ этих равенств находятся также и силы реакции связей. Допустим, в теле имеется неподвижно закрепленная прямая, вокруг которой оно способно вращаться. Выбрав эту прямую в качестве оси z (фигура 54), зафиксируем на ней начало О, к к-рому приведем систему сил, приложенных к телу. Действие равнодейств^чощей силы F очевидно уничтожится реакцией неподвижной оси: главный же моментный вектор 31 метров б. разложен на компоненты М_х, М_у, М_гСилы пары, момент которой равен 31 _х, параллельны оси у и приложены к точкам неподвижной оси, вследствие чего действие их уничтожается реакцией оси;точ-но так же уничтожается действие пары, момент которой равен М_у. Остается только пара с моментом М_г, вращающая тело около оси г; мо- фигура 54.

мент M_z называется вращающим моментом. Для того чтобы рассматриваемое тело находилось в равновесии, необходимой достаточно,чтобы З1₃=0, то есть, как видно из (179”), чтобы

2(ач,Г₍-»,Х,)-0. (183)

1

Т. о. вместо 6 ур-ий (179) и (179”), необходимых и достаточных для равновесия системы сил, приложенных к свободному телу, мы здесь имеем лишь одно необходимое и достаточное условие для равновесия. Остальные же пять ур-ий определяют силы реакции оси, приложенные к телу, которые очевидно состоят из силы — F и пар, моменты которых равны —М_х ж—31 у. Если ось О_г может перемещаться вдоль своего направления, то уравнения (183) недостаточно для равновесия тела, необходимо еще, чтобы

Ζ=2^Ζί=°, (184)

1

т. к. в этом случае не может возникнуть сила реакции вдоль направления оси, которая

уничтожила бы действие силы Z. Если тело имеет только одну закрепленную точку О, то, приведя систему сил к этой точке, нетрудно видеть, что сила F уничтожается реакцией неподвижной точки, так что остается пара момента М. Следовательно для того, чтобы тело в рассматриваемом случае находилось в равновесии, необходимо и достаточно, чтобы М=0, то есть, как видно из (179"), чтобы имели место следующие 3 ур-ия:

1

π

2№-®_г2_г)=о 1

2(®,г₍-»А)-о

(185)

Т. о. при паличии тела, имеющего неподвижную ось вращения, необходимо и достаточно дня равновесия одно условие (183); если эта ось может перемещаться вдоль собственного направления, требуются два, условиями^! 83) п (184); если же тело имеет лишь одну неподвижную точку, требуется уже для равновесия тела три условия (185).

Отсюда следует, что чем тело свободнее, тем больше условий, налагаемых на силы при равновесии тела. Тело, имеющее неподвижную ось, обладает одной степенью свободы, так как положение тела определяется одним параметром—углом поворота тела около оси; в соответствии с этим имеется только одно условие равновесия. Если эта ось может перемещаться вдоль своего направления, то тело обладает уже двумя степенями свободы, и в связи с этим имеются два условия равновесия тела. Если тело наконец имеет одну неподвижную точку, то, так как положение тела определяется тремя параметрами (смотрите Координаты), имеются 3 условия равновесия и т. д.

Допустим, что имеется и материальных точек А_г, Α_ζ, ., А_п, координаты которых соответственно х_ъ Ух,-гт, ж₂, у_г, г₂, .; х„. у_п, т_пи к которым приложены силы F_u F₂, ., F_n. Допустим далее, что эти точки находятся под воздействием нек-рых связей, что аналитически выражается в том, что 3 п координат точек связаны между собою некоторым числом уравнений:

ίι (Х Уи гг, Ж2, у2, г2;.	‘9 У 419 %п) 0 1
.. · (ΐ«Ό
ίρ (®1» Vh Zl Х2ч У2, %2ч ··	· 9 Упч 2п) 0 ^

число которых пусть будет р. Из общего числа Зи координат 3п—р м. б. взяты совершенно произвольно, а остальные р координат м. б. выражены через произвольно взятые при помощи ур-ий (180). Поэтому число 3п—р и определяет степень свободы рассматриваемой системы точек. Очевидно, что р не м. б. больше 3п. Если р=3п, то координаты всех точек системы вполне определяются из (186>, то есть система неподвижна; если же р=0, то все точки системы свободны.

Пусть равнодействующая всех реакций «вязей, действующих на какую-либо точку Αχ системы, равна R, (г=1, 2,в), так что ата точка находится под действием силы,

равной Fj+И;·. Следовательно для того чтобы вся система находилась в равновесии, необходимо, чтобы

Г, + В,- 0 (г =1,2.п), (187)

что равносильно наличию Зи ур-ий Χ, + Χ,-Ο; Υ,· + У<=0; Z₍ + Z*=0

(i=1,2,., η), (187)

где X_t, Y, Zj—модули компонент по осям координат. Выше бы ίο показано, что в случае одной несвободной точки сила И будет нормальна к кривой или к поверхности, осуществляющей связь, и что следовательно полная работа Т силы Л равна по (158) нулю:

<№=ЛМг=0; Т=Jn-dr=0.

Несмотря однако на то, что при наличии системы несвободных точек реакции связей м. б. совершенно другие, чем реакции кривых линий или поверхностей, условие (158) имеет место и в данном случае, так что F_i dr_i=0, и следовательно

П,

2 JJ_rdr,.=0. (188)

1

Последнее ур-ие, являющееся основным уравнением движения системы несвободных точек, м. б. интерпретировано след, обр.: реакции связей, действующих на систему материальных точек, не могут в своей совокупности ни поглощать ни давать работу, хотя для отдельных сил реакций это является возможным. Это предложение стоит в связи с принципом сохранения энергии, ибо, поскольку осуществление связей не влечет за собой ни затраты энергии ни получения таковой, постольку реакции связей не могут ни поглощать ни давать никакой работы. Исходя из (158), (158) и (188), можно в отношении системы точек прийти к точно таким же выводам, что и в отношении одной материальной точки, а именно: точки рассматриваемой несвободной системы, находящиеся сначала в покое, начинают каждая свое движение по направлению соответствующей равнодействующей сил F_{ и Л(, так что в начальный элемент времени имеем:

П

(F_i+M_i)-dr> 0, (189)

1

или, принимая во внимание (188):

п

2 Fi dr_{ > G. (190

i

Т. о. в начале движения сумма элементарных работ всех движущихся сил F_{ положительна. Если же в числе всех возможных перемещений, допускаемых данными связями, нет ни одного, для которого неравенство (190) имело бы место, то очевидно, что система в движение прийти не может; другими словами, необходимым условием для равновесия системы несвободных точек является неравенство:

2 (IV ^)=5 0, (191)

1

где символом 6г₍ обозначены возможные, или виртуальные, то есть допус-

каемые связями, элементарные перемещения точек, в отличие от действительных элементарных перемещений точек, обозначаемых dr_t. Неравенство (191) выражает т. н. п р и н-цип (начало) возможных перемещений, или принцип возможных, или виртуальных, работ (Бернулли, 1717). Пользуясь ф-лой векторного исчисления, неравенство (191) можно представить еще. и в следующем виде:

Г?

2 (Х_{ вщ + Y-i S_Vi + Ζ, δΖι) ϊ= О, (191)

i

где д.т_{, <5ц_{, δζ_{,—модули компонент по осям координат вектора 6г,·. Если уравнения связей не содержат неравенств, а даны например равенствами вида (18G), то всякой системе возможных перемещений соответствует система возможных же, но противоположных перемещений — &г_ь так что, если система точек находится в положении, при котором

П

2 ^Fi ^Sri < 0, то будет иметься система пере-1.

п мещений, для которых ^ 2^ · 0r_t > 0. В этом 1

случае равновесие будет иметь место, если при всех возможных перемещениях существует равенство:

п

·*·<-

1

= 2 {Х_г *е_г + Y, 0y_t + Z_t Szi)=0. (192)

i

Значение принципа возможных перемещений заключается в том, что при его применении нет надобности знать для определения условий равновесия несвободной системы точек ни характера механизмов, осуществляющих данные связи, ни величины реакций их; для этого достаточно знать лишь все возможные элементарные перемещения точек системы при данных связях.

Допустим в частности, что все возможные перемещения, или вариации пере-м ещений, й“_г совершенно произвольны, то есть что точки системы свободны. Тогда, положив все вариации координат 6х_г, 6ц_и δζ_χ, <fe₂,. равными нулю за исключением δζ_η, получим из (192):

Ζ_ηδζ_η=0 или Ζ_η=0.

Точно так же получим:

Х_г=0; Υ₁=0; Ζ₁=0; Х₂=0 и т. д., так что вместо равенства (192), выражающего условия равновесия, получим равенства:

-Pi=0; JF,-0; JF„=0, что конечно совпадает и со сделанными ранее выводами. В противоположном крайнем случае, то есть когда все точки систем не могут менять своего положения, так что: 4г_г=0, (г= 1,2,3,.,п), равенство (192)тождественно удовлетворяется при всевозможных силах .F,·, то есть система будет в равновесии, каковы бы ни были силы F_t, что конечно очевидно.

В общем же случае при наличии р ур-ий связей (186) для системы точек, имеющей 3п — р степеней свободы, можно прийти от ур-ия равновесия (192) к ур-иям равновесия,

связывающим компоненты сил F₍ с координатами точек, след. обр. Из общего числа Зп вариаций 6.r_it δζ_{ (г=1, 2. ., г) выберем пршзвол1но Зм— р вариаций, придав им произвольные значения; остальные же р вариаций выразим через первые при помощи ур-ий (186), для чего нужно будет совместно решить относительно желаемых вариаций систему р однородных линейных ур-ий, полученных из (186):

W₁^0x^ ⁺ Wi^Syi+ ··· ⁺wJ^Zn=Q

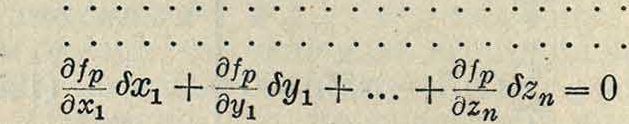
(193)

Подставив затем найденные р вариаций, выраженные через 3п—р произвольных вариаций в равенство (192), получим сумму элементарных виртуальных работ сил F₍как однородную,линейную функцию от 3п—р произвольных вариаций. В виду же произвольности этих вариаций придем способом, аналогичным вышеприведенному, к выводу, что коэф-ты при произвольных вариациях’ равны нулю. Таким образом получим Зп—р ур-ий равновесия, связывающих координаты точек системы с компонентами сил F_itто есть получим число условий равновесия,равное степени свободы системы, что и обобщает сделанный нами вывод, касавшийся условий равновесия твердого несвободного тела.

Выполнение всех указанных выше действий на практике однако весьма утомительно, вследствие чего применяется еще и следующий метод. Умножив ур-ия (193) соответственно на р множителей Ац, Я₂, А₃. λ_ρ, величины которых определяются впоследствии, и сложив эти результаты с ур-ием (192), получаем:

Щ + b ^ай + - + э ** +

г=1

+¥(^+^+-+^ΐκ·+

+ 2¹[^Zi + ^Я1 Ш ⁺ · · · + ^λν Jsf) ^6zi⁼°· (¹⁹⁴>

Последнее равенство справедливо при всевозможных значениях λ и для всех возможных перемещений системы. Выберем множители так, чтобы коэф-ты при р первых вариациях, начиная от δχ_ι, аннулировались. Тогда в левой части ур-ия (194) останутся только 3п—р вариаций, и притом совершенно произвольных, вследствие чего коэф-ты при них аннулируются. В конечном итоге следозательно все сводится к тому, что коэф-ты при 3п вариациях в ур-ии (194) равняются нулю, то есть что

Oh,

² дХ{ ’

Xi + λ^ + λ,

У-1 + Я 1-Й + Л.Й+-.

Z_i + A₁-g + A₂^+.+A^=0,

j_ 3 ?ίρ. ₌ о

^{+ Л}Р fact ^υ

-^ι.τί-°

(195)

^: dZi ¹ · · ¹ ΡQzj

Если исключить из последней системы множители А, то получатся опять Зп—р ур-ий равновесия. Указанный метод нахождения условий равновесия носит название метода неопределенных множителей (Лагранж). Сравнивая ур-ия (195) и (187), можно сразу же получить компоненты сил реакции:

V ч О/,.. о/_{2 |}. df_v

] ^{+ +} ·" ^+лРдх

··· +7

¹ay_i ¹ "»0у₍

Z^+λ^ + .+λ,

Роу,

^dJl

Pdz,

.1(г=1,2,./.,«). (196)

У

До сих пор мы разделяли силы, действующие на систему, на две категории: на силы движу-, щие F и силы, реакции связей Щ. Можно однако действующие на систему точек силы разделить на другие две категории, а именно: на силы внешние и силы внутренние. Внешними по отношению к данной системе называют силы, которые исходят из точек, не входящих в данную систему; внутренними же силами называются си ты, источниками которых являются материальные точки, сами входящие в состав данной системы. Так, если рассматривать систему, состоящую из земли и луны, то силы притяжения солнца будут силами внешними, а силы взаимного притяжения земли и луны— силами внутренними. Если же в состав системы включить также и солнце, уо все перечисленные силы будут силами внутренними. Группировка сил на движущие силы и силы реакций не совпадает с группировкою на внутренние и внешние силы, т. к. бывают движущие силы внутренние и внешние, точно так же, как и силы реакции связей бывают внешними и внутренними. Характерной особенностью сил внутренних является то, что они, на основании принципа равенства действия и противодействия, попарно равны и противоположны. Т. к. вследствие этого все внутренние силы во всяком случае взаимно уравновешиваются, то при равновесии системы и все внешние силы должны между собою взаимно уравновешиваться. Последнее предложение находит многочисленные применения при определении законов равновесия нетвердых систем, как например жидкостей, газов и тому подобное.

Динамика системы точек и твердого тела. .Для того чтобы обобщить вышеприведенные выводы так, чтобы законы движения материальной точки и законы равновесия системы материальных точек оказались частными случаями более общих выводов, рассмотрим систему п точек, массы которых т_ъ ш₂, ., ш_п находятся под воздействием следующих связей, которые могут зависеть также.и от времени <:

U (*1, У 1> ^zli *2> · · · > ^zni t) — О

ίΐ (®1> 2/ΐ! ^ζ1> ®2) · - ; ί)=0

(197)

ίρ (*1! 2/ΐ> ^Ζ1! 3-21 ···! ^ζη t) — 0

Пусть кроме того к точкам системы приложены соответственно силы F^F^,., F_n. Если прибавить к этим точкам силы инерции —т₁а₁ —т_га_г, ., то на оснорании принципа Д’Аламбера, выраженного формулою (153), точки системы будет находиться в равновесии, вследствие чего мож т быть в свою •очередь применен принцип возможных пе ремещений, выраженный равенством (192). Т. о. как синтез обоих принципов получаем:

П

2 (Fi - т_{щ) Sr_t=0, (198)

1

или, что то же самое:

Σ [(*<- ^mi if) *% + (Υϊ- Щ Д Sy_t +

+ {^Zi-^mi^dfi) **/]=0. (1980

Вместо ур-ия (198) имеем также, пользуясь системой ур-ий (195), заменившей, как мы видели, ур-ие (192):

Σ*	d^xi	+	h	Ofi Ox,·	+
+ ^2	Ofz, dXi "Г ···	+	Ap	Sfp dXi	= 0
	~md2yi-г αμ	+	К	Oh dyi	+
+ К	dh, Ovi + · · ·	+	Яр	dfp дуг	= 0
zr	d2Zi	+	h	dfi dzi	+
+ Я2	i dzi "τ’ ‘"	+	Яр	dfP dzi	= 0

(г=1,2, .,№).(199)

Последние ур-ия носят название уравнений движения Лагранжа 1-го рода. Умножив 3п ур-ий (199) соответственно на 6х₍, ду₍, όζ₍, сложив результаты и приняв во внимание ур-ие (193), получаем снова ур-ие (198) или (198). Исключив вели чины λ, (j — 1, 2,

р) из (199), получаем

3п — р линейных ур-ия между проекциями ускорений тачек и компонентами двил-Еущих сил. Эти ур-ия вместе с р ур-иями связей и определяют однозначно движения точек системы. Ур-ие (198) удовлетворяется любой систем! и возможных элементарных перемещений 0Г(, если последние удовлетворяют системе ур-ий (193). Если же рассматривать систему элементарных перемещений dr_t, которые в действительности имеют место за промежуток времени dt, то они должны удовлетворять системе ур-ий:

«i,

дх.

Ш. ^dXi + + fzi ^dz +

дх

4- 91i ή_ζ

⁺ dz_n ^aZ

- dx2 -j-. -f-

+ fdi=0

(j=1, 2, ., n), (200) отличающейся от ур-ий (193) тем, что она содержит еще и члены dt. Вследствие этого истинные элементарные перемещения dr,· не совпадают в общем с возможными элементарными перемещениями Sr_i системы. Таким сбразом в обшем нельзя смешивать перемещения dr_t и Sr_t. Если же ур-ия связей (197) не содержат в явной форме, то члены dt в ур-ии (200) исчезают, а вместе с тем исчезает и различие между действительными и возможными перемещениями системы. В последнем случае можно следовательно писать вместо (198) также:

П

2 (Fi - т_{а^ dr i=0. (201)

1

Т. к. на основании (125)

2 dr₍= 2 ^dLi·

(202)

то имеем из (201):

П 71

2 (Fi dr i)=2 dLi=dL, (203)

1 1

n

где L=2 L_u T. e. в этом частном случае

i

сумма эл^м^нтп рных работ всех движущих сил равняется сумме диференциалов живых сил точек системы. Интегрируя (203) в пределах от до ί₂, получаем, что полная работа всех движущих сил за какой-нибудь промежуток времени равняется изменению суммы кинетич. энергии Rcex точек системы за тот же промежуток времени. Эт о предложение имеет место, если ур-ия связей не содержат (в явной форме, в противном же случае сумма работ сил реакций при действительных перемещениях точек системы не равняется нулю, поэтому надлежит учесть и работу последних сил. В общем среди движущих сил M,· могут быть как потенциальные, так и непотенциальные силы. Сумма элементарных работ первых сил равняется по (133) — dU, где U=ZUj, a U ₃—силовые функции, соответствующие имеющимся потенциальным силам; сумма элементарных работ непотенциальных сил:

V

2 F-drk=dA,	(204)
k—l
где F—непотенциальные силы, торых V. Тогда имеем:	число ко-
71 2 Ft-dVi=-dU + dA, 1	(205)
или по (203):
dL=— dU + dA, d(L + U)=dA.	(206)

Так как кинетич. энергия L системы зависит от скоростей точек и так как эти скорости— понятия относительные, то и кинетич. энергия системы точек есть также величина относительная, зависящая от состояния системы отсчета. Допустим, что имеются две системы отсчета: одна с началом О, не связанным с данной системой точек, и другая с началом О, неподвизкно связанным с системой точек. Пусть и rt (фигура 55) суть радиусы-векторы, опреде-Фигура 55: ляющие положение точ ки А _{ по отношению к системам О и 0 соответственно, а г₀—радиус-вектор, определяющий положение точки О по отношению к системе с началом О. Тогда имеем:

Τί ^{= ϊ}*ί+ ^го> или, что то зке самое,

ж“=ж; + я»; 2h=Vi + У o’, я»=ζί + z_tt.

Беря производные по времени от последних равенств и обозначая производные точкою над соответствующей переменной, имеем:

£;= щ + ж₀; y_t=yi +· у₆; zi-ζ + z‘₀. (207)

Для кинетической энергии L системы точек, принимая во внимание (26):

п п

^{L =} 2 Σ ^W*^V* ⁼ 2 Σ ^W* № + и + *?) -1 1

п

= + *о)² + (Уг + УоУ+ (zi +io)²] -

1

71 * η η

= { 2 ^m‘^v? + J ^v0 2 ^mi ⁺ 2 ^m&»xi +

1 1 i

71 П

+ ^ЩУоУг + 2^т**<Я, (208>

1 1

где

ν’=]/х² + у² + г² и г-₀=]/ж§ + у + ζ²

суть линейные скорости точки A_t по отношению к системе О и точки О по отношению к системе О соответственно. Пусть далее координаты центра масс системы точек по отношению к системе отсчета с началом О будут х, у, г. Тогда на основании (171):.

x-£m_i=]У]т_гж; у -2^mi= г · 2 ^mi ⁼ 2 ^mi ^Zi-

Если точка O совпадает как раз с центром масс, то так как ж=0, у=0, г=0, получимг

2ntiXi=0; 2 ^тгУг=0; 2 ^т(₍=0, и следовательно

2 VhXi=0; 2 ^miVi ⁼ °> 2V-0.

В этом случае следовательно три последних члена левой части равенства (208) равны нулю, так что получаем:

71 71

L - vl 2 т_{ +12 туу. (208)

i 1

Т. о. кинетическая энергия системы точек равна сумме кинетической энергии центра масс, если в нем сосредоточить массу всей системы, и кинетической энергии системы в ее движении относительно системы отсчета, имеющей начало в центре масс.

Основной динамический закон движения, выраженный ур-ием (198), допускает еще ряд других формулировок, имеющих в конечном итоге один и тот зке физич. смысл. К числу последних принадлезкит так называемым принцип наименьшего действия., или принцип Гамильтона. Так как ур-ие (198) справедливо для любого момента времени, то, умнозкив ур-ие на din проинтегрировав результат в пределах от t₁ до ί₂, получим:

j^!«[S(i-mg)a+S(r-»g)_i!,₊

h

+2(^z-^mEH=°> (²⁰⁹>

где индексы г для упрощения опущены. В последнем ур-ии следует рассматривать как функции времени не только координаты x_irУь,г_{, но и вариации дх_{, ф/_г, όζ,·, что вытекает из следующих соображений. Допустим# что все координаты точек зависят не только от ί, но еще и от нек-poro параметра у. Опре-

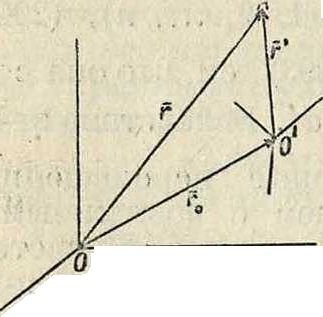
деленному значению η соответствует тогда определенное движение точки Af, значению же η+δη соответствует нек-рое бесконечно близкое соседнее движение, к-рое конечно в общем не удовлетворяет уравнению данного движения. Действия d и δ, соответствующие изменениям величин по времени и по параметру, независимы друг от друга, вследствие чего можно писать:

(210)

dSx dx ~dT~°~dt

дх причем вариации δχ=δη, будучи в любой момент произвольными, должны однако удовлетворять условиям (193). Применяя полученную формулу (210), имеем, интегрируя по частям:

² - Jdt -

h

dx

dt

dSx dt ⁼

л "i.

-[£“], -J" f- - «

i A1

“ [ж *]!-

(211)

· *1

Если предположить, что вариации всех координат равны нулю при t=t_x и t=ί₂> ^то

tdx с Тг

=0, и тогда имеем из (211):

*2

δχ=-

ЛМж) t²¹¹)

С другой стороны, по (205) имеем:

2 (Z δχ + У ду + Ζδζ)=-δϋ+όΑ.

(212)

Подставляя (211) и (212) в (209), получаем:

12

J dt (δΗ -I- δ A)=0, (213)

где H=L—U. Величина Η называется к и-нетическим потенциалом, или ла-гранжевой функцией системы. Равенство (213) и выражает принцип Гамильтона. Т. к. формулировка этого принципа не зависит от системы координат и т. к. кине-тич. потенциал Н и работа непотенциальных сил А встречаются во многих областях физики, то применение этого принципа встречается очень часто при исследовании вопросов не только М. т., но и электродинамики, термодинамики и тому подобное. Очень часто положение точек системы определяется не при помощи прямолинейных ортогональных координат, а при помощи других координат: полярных, цилиндрических и т. д. (смотрите Координаты), которые удобнее применять при данных условиях движения. Как и в приведенных выше случаях, число таких координат, которые обозначим через д_г, q₂, ., должно равняться степени свободы системы, если они независимы друг от друга. Координаты же x_t, th, г» суть тогда определенные функции от q_u q₃, .,аесли связи зависят от времени, то и в явной форме от t:

ж»=“,(?!. g* ···; t) i

У1=Ус(Чи ···; О >· (214)

«i=%г (qi, q2,.; t))

Если связи от времени не зависят, то, как видно из (214), полные производные их по t, т. e. v_x, v_yv v_Z{ — однородные линейные функции от, коэф-ты при которых могут содержать qj. Так как, с другой стороны, вариации δχι, dy_h 6г_г—однородные линейные функции от 0qj. а 6А—линейная однородная функция от &,·, Sy_t, δζ{, то δΑ м. б. представлена в следующем виде:

δΑ=0₁6q₁ -f- 0₂6q₂ -f- 6₃dq₃ -j-(215) причем δΑ может содержать элементарные возможные работы как потенциальных, так и непогенциальных внешних сил. Так как величины Oj играют ту же роль, что и компоненты Х_{. Y₍, Z в формуле (212), то они называются обобщенными компонентам и сил.

Нетрудно усмотреть, что кинетич. потенциал Я представляет собой в рассматриваемом случае ф-шо 2-й степени от производных qj, коэф-ты к-рьтх суть ф-ии от q, а возможно и от t. Т. к. при вариировании координат </,· время t не меняется, то

_ХТТ ОН е“. ОН С* I I №= — <fyi + + ··· +

dQ. i dq 2

. дН р, дН о. _Г4Ч

+ 9«) ^{6qi +} Эва ⁺ · · ^¹⁶⁾

Из (216) имеем, принимая во внимание, что

<*?

dt dt

v доп ^J J dqj dt

e-¹·²·-)· ^(2I7)

h ^J

так как при t=fj и ί=i₂ все вариации dq$ равны нулю. Подставив значения (216) в (213), получим, принимая во внимание (217). а также и то, что 4^· независимы друг от друга:

А ™ ₌ е

dt dqi dq₁

d /дН дН

dq₂

dt dq₂

dQz

= θ„

> ·

(218)

Последние ур-ия называются уравнениями движения Лагранжа 2-го рода. В качестве примера рассмотрим движение свободной материальной точки, положение которой определяется цилиндрич. координатами г, φ, ζ. Из (215) имеем:

δ А=в_г дг + 0₂ δφ + θ₃ δζ. (219) При отсутствии потенциальной энергии

Так как

X=Г COS φ И у=Г Sin φ,

ТО

άζγ dt ‘

= (r COS ψ — r sin φ <py- + (r sin φ + r cosy ?>)²-b

^2 _ ^.2 -|- γΖ φϊ -j-

следовательно

Я=у (г² + г²??² + г²). Отсюда получаем, сообразно (218): дн_ дг дП

_{: тг}

—=тг φ² дг д<р дН

дг

= mr-φ

дН

= 0

-=тг эк

dz

= 0

6_г=_dt (тг) — mrq)²

θ₂=_d- (τηΗφ)

β,

(220)

-3 i_d( («*)

Выше мы разделяли все силы, действующие на систему материальных точек, находящуюся в покое, на силы внутренние и силы внешние. Аналогичное подразделение можно сделать и в отношении сил, действующих на движущуюся систему, причем отмеченное выше основное свойство внутренних сил сохраняется и η данном случае. Обозначая внешние силы через Ф_г, имеем, применяя к движущейся системе принцип Д ’Аламбера, на основании ур-ий (179):

η

2 (⁰i - ^mi^ai)=0, (220)

1

2[г_г.(Ф_г-т_Л)]=0, (220”)

i

то есть во время движения системы точек силы внг шн ie и силы инерции в любой момент времени взаимно уравновешиваются. Ур-ия(220 и 220”) применимы как к ί вердым, так равно и к нетвердым системам точек, как то: к га,зу, жидкости и т. и. и в частности к твердым телам. Т. к. из (171) следует, что

71 П

d²rо. хл. d²rs

dt²

Ш

= 2 ^mi=2^mi^a>’ (²²¹)

где m= 2 ^mi—масса всей системы точек, то,

вставляя (221) в (220), получаем:

т

^dirA= У ф. dt2 XI

(222)

то есть что ц. т. системы материальных точек двюкется так, как будто масса всех точек системы собрана в нем и как будто все внешние силы, действующие на систему, прилозке-ны непосредственно к этой точке. Отсюда видно, что па двизкение центра тяжести системы внутренние силы никакого влияния не оказывают. Из (220) имеем также:

⁽²²³⁾

1 1

то есть производная по времени от суммы количеств движения точек равняется сумме (векторной) внешних сил, действующих на систему. Если все внешние силы равны 0 или

П

если 2 ^фг⁼ 0, то из (223) имеем:

1

η

2 mfli=Const.

i

η

Τ. о., если 2 Φ_?·=0,το сумма количеств дви-1

жения точек системы, называющаяся также результирующим количеством движения, остается во время движения без изменения. Особенное значение имеет последнее предложение при исследовании .явления удара (смотрите Удар). При2 Ф*=0 имеем также из (222):

0, (224)

то есть если на систему точек не действуют никакие внешние силы или если действуют силы, сумма которых равняется нулю, то центр тяжести системы двизкется прямолинейно и равномерно. Из (220”) имеем далее:

2=2[**«^ф<].

или, так как [υν]=0,

/_г2^^т^=2 (^{223 * 225})

то есть производная по времени от суммы моментов количеств двизкения точек системы по отношению к какой-либо точке равняется сумме моментов всех внешних сил по отношению к той зке точке. Сумма моментов количеств двизкения точек называется также главным моментом количества движения системы. Если в частности имеется свободное твердое тело, причем внешние силы Ф₁ даны, то уравнения (220) и (220”) вполне определяют движение тола, т. к. число этих ур-ий, равное 0, соответствует 6 степеням свободы тела. Допустим однако, что тело, к к-рому прилозкены данные силы, не свободно, а имеет одну неподвизкную ось вращения, к-рую мы примем за ось Οζ. Взяв на этой прямой произвольную точку О, приведем к ней всю систему сил Ф, так что получится одна равнодействующая сила Ф и пара момента М. Аналогичным образом моэк-но к той зке точке привести и неизвестные силы реакции оси, получив силу Ф и момент М. Из всех шести ур-ий (220) и (220”) только последнее не будет содержать компонент неизвестных сил реакции, а именно:

2 (226) а следовательно только оно и определяет движение тела, в соответствии с одной степенью свободы его. Параметром, определяющим положение тела, слузкит угол поворота φ, который образует плоскость в теле, проходящую через Οζ, с плоскостью, неподвижной в пространстве и проходящей через ту зке ось Οζ. Обозначая расстояние точки (ж,·, y_itz_t) до оси Οζ через ρ_{·, имеем:

Xi=eiC08<p; у i=Qi sin ψ (227) sin ?> · gj; fp=Qi cos Ψ Г, (228)

//2γ * · *·

= - Qi COS φ φ² - Qi Sin ψ · φ;

ТЯГ ⁼ ~ ^в‘ ^Sin Ψ Ψ² + βί^Οβφ- φ. (229) Вставляя равенства (227) и (228) в (226) и принимая во внимание, чю угловое ускорение ψ постоянно для всех точек тела, получаем:

|?Je²dm=M_s, (230)

где знак 2 заменен знаком J в виду того,

что суммирование произведено по всем точкам объёма тела, dm представляет массу .элемента объёма, находящегося на расстоянии s от оси Oz.

Величина

(231)

I_z= I* Q*dm

(V)

называется моментом инерции тела относительно оси Oz (смотрите Момент инерции). Т. о., обозначив угловое ускорение через Θ, имеем:,

Θ·Ι_Ζ=Μ(232) Полученная формула (232) аналогична формуле (107) прямолинейн. движения, причем вместо массы здесь имеется момент инерции, вместо линейного ускорения—ускорение угловое, а вместо силы—вращающий момент внешних сил. Интегрирование ур-ия (232) производится точно таким же способом, как и при прямолинейном движении. Кинетич. энергия тела получается в рассматриваемом ^рдучае из следующего общего выражения:

^L~ s=if ч©²+®г+(э²]’ ^

(V)

00

из которого,. воспользовавшись формулами (228) и обозначив угловую скорость через си, имеем:

<²³⁴)

Если в какой-нибудь момент ί₂ кинетич. энергия тела равнα= ^ 1р>, а в момент

ί₂ равна 1/_а=~ J₂co|, то на основании закона живой силы, выраженного ур-ием (125), имеем:

T- hfl» (235)

Из шести координатных ур-ий (220 и 220”) остались еще неиспользованными пять ур-ий, определяющие реакции оси, а именно:

Ф=2^тг«г-Ф, (236)

^жх “ 2 ^тг (уi τΜ, - ~Ж) - ^М* М_у=^ш^^-х₍Щ-М_у

, (237)

которые и определяют Ш=Ж + Ж и Ф. Если в частности все силы Ф равны нулю, то из (232) имеем:

d<p

Θ=0 и

dt

со=Const.

(238)

В этом случае реакции оси определяются ур-иями:

шм_{

ф=2

2

М’_х

^Му= 2 ^mi{

dt2 J

d^Xi

d²Xi

(239)

Вставляя в Ф_х=2^m* avi ’ ^{и ф}у ⁼ 2

m.

d*Vi

* dO

значения и

αί*¹

из (229), получим:

^ф*=- ϊ>³ 2^{MiXi ф}г=~ 9>² 2 ^w*-2/*· I

(240)

или на основании (171):

Фх~- Ψ^2χ0 2 ^mi=- ^ω2χ0 2^теА. (241)

Фу=-<Р²Уо 2^тг=-^с°²г/о 2^тА Т. к. проекции центробежной силы инерции точки, масса которой т, по осям координат суть arx · т и <о-у т, то согласно (241) результирующая реакция связи Ф, противоположна центробежной силе инерции центра тяжести, в котором сосредоточена вся масса тела и который вращается с угловой скоростью со. Если ось вращения проходит через центр тяжести тела, то, как это видно из (241), Ф=0, то есть в этом случае результирующая сила реакции оси равна нулю, но вращающие моменты М_х и М_у в общем случае не равны нулю:

м;--2«л1пг

Му=+ 2 »4*1 Ж Г

Т. к. далее ~=0, то из (229) имеем:

(242)

d*Xj

dia

d²Vi

dt²

= - ^χί¥^ι

= - У/P² J

(243)

Вставляя значения (243) в (242), имеем:

М_х= 2W^U 9>^а2™i^ziVe= Vf .(244) м;=-2«да?>^!= -?>³2miXiZe=-lJ?j

где 1_уз и I_xz—т. наз. центробежные моменты инерции. Т. о. даже в рассматриваемом частном случае для того, чтобы осуществить неподвижную ось вращения тела, нужно будет приложить два вращающих момента — М_х и +М_у если же ось сделать свободной, то, несмотря на отсутствие движущих сил, ось вращения все же неподвижной не останется, а будет перемещаться определенным образом в пространстве. Лишь если центробежные моменты инерции тела 1„ и I_yz будут к тому же равны нулю, ось останется неподвижной в пространстве и без всякой поддержки. Такая ось вращения тела называется свободной, или перманентной.

Графостатина. Помимо вышеприведенных методов определения условий равновесия системы сил при помощи составления и решения определенного числа ур-ий, то есть помимо методов аналитических, широко применяются, в особенности при решении практических задач статики, методы графические, составляющие предмет изучения графической статики, или графостатики. Каждый из этих методов имеет свои преимущества и свои недостатки. Аналитич. метод дает в общем более точные результаты, достигаемые однако путем сложных и утомительных вычислений, связанных с составлением и решением ур-ий, выражающих условия равновесия. Графический метод, наоборот, давая более быстрые результаты и отличаясь легкостью усвоения и запоминания, дает однако менее точные результаты. Во всех тех случаях, когда особой точности результатов не требуется либо когда в сложных случаях приходится делать допущения, понижающие точность аналитич. методов, графич. мето-

ды обладают несомненными преимуществами перед аналитическими. В последнее время графич. методы находят применение также в области динамики, составляя предмет изучения графической динамики. Однако во многих случаях применение одних лишь графических методов не является достаточным для решения поставленных задач статики, так что приходится применять смешанные графо-аналитические методы. В особенности это имеет место при определении неизвестных усилий в так называемым статически неопределимых системах (смотрите Фермы), когда помимо общих ур-ий статики необходимо принимать во внимание еще и упругие изменения системы. Развитие графостатики связано с развитием т. наз. проективной геометрии. ’ Основными методами для графостатики являются построения силового многоугольника и т. наз. веревочного многоугольника (смотрите).

Если имеются две силы £¹1 и F₂, приложенные к двум различным точкам I и II (фигура 56) и лежащие в одной и той же плоскости, линии действия которых пересекаются в некоторой точке 1ΙΓ, находящейся вне пределов чертежа, то прямое применение приведенного метода полного решения не дает. В самом деле: построив от какой-нибудь произвольной точки 0 силовой мн-к 012, так что ^

01=и 12= F, получим равнодействую-

m;yioF=0,2 лишь по величине и направлению; линия же действия F остается неизвестной. Для определения положения последней приложим к точкам I а II две равные и прямо противоположные силы Qx и Q₂, так что Qx= — Q₂. Складывая по правилу параллелограмма попарно силы Ρχ и Q_x, F₂ и Q₂, получим силы Их и И₂, одновременное действие которых точно такое же, как и действие

^г сил Ρχ и F₂. Если силы Qx и Q₂ достаточно велики, то, продолжив линии действия И_г и Н₂, можно получить точку пересечения III, находящуюся в пределах чертежа и через которую очевидно проходит искомая линия действия ^параллельно найденному направлению 02. От той же точки О можно построить другой силовой мн-к 012 соответственно силам Ηχ иВ₂,такчто01’=И_Х и 12=И₂, --> -->

причем очевидно, что 11=Qx и Т1=Q₂. Отрезки 02 nil представляют собой диагонали четырехугольника 0121Ό, точно так же, как отрезки III III и III суть диагонали четырехугольника I III II ΙΙΙΊ. Нетрудно также заметить, что между этими четырехугольниками существует взаимно обратное соответствие, к-рое состоит в том, что каждой стороне или диагонали одного четырехугольника соответствует параллельная ей сторона или диагональ другого четырехугольника, а каждой точке, в которой сходятся три направления одного четырехугольника, соответствует тр-к с параллельными этим направлениям сторонами в другом четырехугольнике. Так например, точке II соответствует тр-к 121, а точке 1 соответствует тр-к II I III. Во взаимно обратном соответствии этих фигур и проявляется тесная связь, существующая между построениями графостатики и проективной геометрии. Таким образом, чтобы полностью получить равнодействующую F, достаточно поступить след, образом: построив силовой мн-к 012, возьмем произвольную точку С,

называемую п о л ю с о м, и соединим ее со всеми вершинами силового мн-ка прямыми, или лучами, СО, Cl, С2. Проведя далее прямые: 011) СО до пересечения в точке I с линией действия F^; IIIHC1 до пересечения в точке II с линией действия F₂ и II HI I С2, получим мн-к 0 I II III, крайние стороны которого пересекаются в точке III, через к-рую проходит линия действия силы F=02. Мн-к 01 II III называется нитяным, или веревочным.

Приведенное построение можно распространить и на более общий случай. Допустим, имеется плоская система п сходящихся или не сходящихся сил F_lt F₂, ., F_n. Пусть например п=4 (фигура 57). Для сил Fx и F₂ найдем вышеприведенным способом все элементы, определяющие их равнодействующую F₁₂, то есть величину, направление и линию действия последней; взяв затем F12 и F₃, аналогичным образом найдем все элементы их равнодействующей F_ls и т. д. Все построение очевидно сведется к следующему. Построив силовой мн-к 01234 и взяв произвольный полюс С, соединим его лучами СО, С1,. со всеми вершинами силового мн-ка. Затем из произвольной точки 0 проведем: прямую 01 параллельно 1-му лучу СО до пересечения в точке I с линией действия силы F_lt прямую III параллельно 2-му лучу до пересечения в точке II с линией действия силы F₂ и т. д. Полученный так. обр. нитяной мн-к вместе с построенным силовым мн-ком дает возможность определить равнодействующие как всех данных сил, так и определенной группы их. Так, для получения линии действия равнодействующей Р₁₂ сил F_t и F₂ достаточно продолжить крайние стороны нитяного мн-ка, соответствующие этой части фигуры, то есть стороны (1) и (3) до их взаимного пересечения в точке III, и провести через 111 прямую, параллельную 02. Be-

личина же и направление определяются —>

вектором 02. Точно так же для получения линии действия равнодействующей F₁₃ сил F_x, F₂ и F₃ достаточно продолжить стороны нитяного мн-ка (2) и (4) до их взаимного пересечения в точке IV и через эту точку провести прямую, параллельную 03 величина же и направление F₁₃ определяются век—>

тором 03 и т. д. Нетрудно видеть, что F_x + --> ——>

+F₂ + F₃ + Fi=OC + C4; отсюда явствует, что всякая плоская система сил м. б. заменена двумя силами, которые действуют по направлениям крайних сторон построенного нитяного многоугольника и равными по величине крайним лучам соответствующей полярной фигуры.

Точно такое же построение можно применить и к плоской системе параллельных

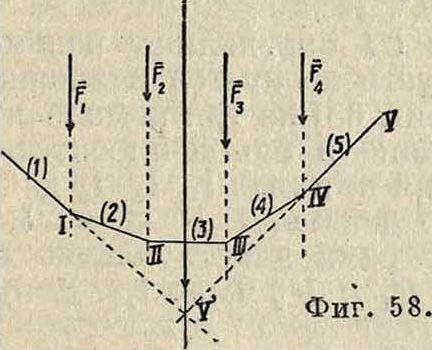
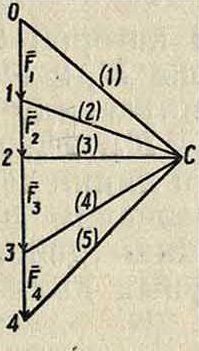
сил (фигура 58 и 59). В этом случае, как это нетрудно усмотреть, все стороны силового мн-ка лежат на одной общей прямой, так что величина равнодействующей равняется алгебраич. сумме сил составляющих.

Как мы видели выше, для того чтобы данная плоская система сил взаимно, уравновешивалась, необходимо, чтобы силовой мн-к был замкнутым, то есть чтобы начало О силового мн-ка совпало с его концом п (фигура 60 и 61). Т. к. вследствие этого крайние лучи полярной фигуры совпадают как по величине, так и по направлению, то очевидно, что крайние стороны нитяного мно

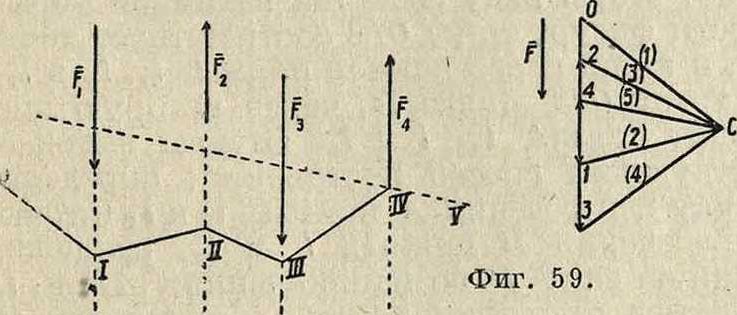
гоугольника будут либо параллельны либо совпадать. Т. к. далее данную систему сил можно заменить двумя силами, равными крайним лучам полярной фигуры, а т^кже в виду того что эти лучи между собою рав-· ны,—в первом случае очевидно система сил приводится к паре сил, а во втором случае—взаимно уравновешивается. Так. обр. для того чтобы данная система сил взаимно уравновешивалась, необходимо и достаточно, чтобы и силовой и веревочный мн-ки были замкнутыми. В случае, когда имеется сходящаяся система сил, замкнутость силового мн-ка является не только необходимым, но и достаточным условием для равновесия. При наличии большого количества составляющих сил нет надобности строить веревоч ный мн-к с полным числом сторон. Для это^ го достаточно предварительно сгруппировать данные силы, заменив их меньшим числом

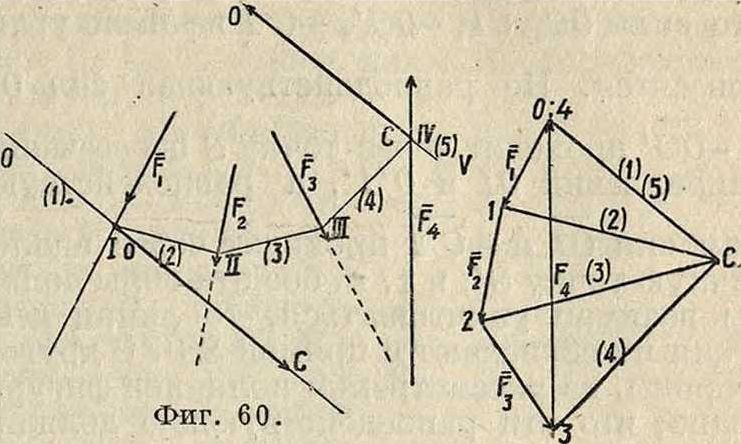
равнодействующих, и уменьшить соответствующим образом число сторон как силового, так и нитяного мн-ков.

Из предыдущего ясно, что.для данной системы сил линия действия равнодействующей занимает вполне определенное положение, а т. к. крайние стороны нитяного многоугольника должны пересечься в одной из точек этой прямой, то следовательно имеется бесчисленное множество точек, по которым это пересечение может произойти. С другой стороны, так как имеется оо² возможностей выбора полюса С и так как каждому полюсу соответствует со нитяных мн-ков, в соответствии со свободным выбором исходной точки 0, то всего имеется оо³ возможностей.

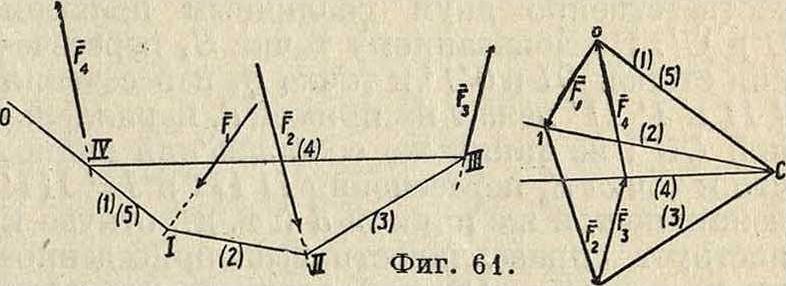
построения нитяного мн-ка, обусловливающих однако лишь оо точек пересечения. Отсюда следует, что между оо³ нитяных мн-ков данной системы сил должны существовать определенные зависимости. Эти зависимости суть следующие: соответствующие стороны двух нитяных мн-ков, построенных для одной и той же системы сил, но при помощи двух различных полюсов С я С (фигура 62), пересекаются на прямой, которая параллельна СС’. Для того чтобы это усмотреть, возьмем одну силу F и, выбрав полюс С, построим для нее полярную фигуру 0С1 и нитяной мн-к О III. Затем, выбрав другой полюс С, построим соответствующие полярную фигуру ОС1 и нитяной мн-к ОIII.

По предыдущему, сила F м. б. заменена ли--> ·——>

бо двумя силами ОС и С1, действующими по

--> -->

01 и III, либо двумя силами ОС и С1, действующими по 01 и Ill. Если же при-

дожить по последним двум направлениям две силы,равные —ОС и —С1,το очевидно, что силы ОС, С1, —ОС, —С1 взаимно уравновесятся. Но равнодействующая сил ОС

и —ОС проходит через точку S пересечения направлений 01 и О I, а равнодействую щая сил С1 и —С1 проходит через аналогичную точку S, и т. к. обе эти силы должны взаимно уничтожаться, то линии действия их совпадают с прямой SS. С другой стороны, из рассмотрения полярной фигуры видно, что эти равнодействующие должны

быть направлены по прямым, параллельным СС, так что SSll СС.

Распространяя эти выводы на общий случай, построим для данной плоской системы п сил F_x, F₂, F_z, ., F_n (фигура 63) два нитяных мн-ка О 111 III. и 0ΊΊΤ1ΙΓ. соответственно двум различным полюсам С и С. По доказанному точка S_x пересечения сторон 01 иΟΊ и точка S₂ пересечения III и I 11 лежат на прямой d, параллельной СС; из таких же соображений видно, что и точка £>₃ пересечения II III и II 111 лежит на той же прямой d и т. д., откуда и явствует справедливость вышеприведенного положения. Отсюда следует, что если закрепить точки пересечения Si, S₂, ., S_nсторон нитяного мн-ка с некоторой прямой I и если поворачивать стороны 01, III, IIIII,. вокруг этих точек так. обр., чтобы вершины нитяного мн-ка перемещались по соответствующим линиям действия сил, то мы получим новые силовые мн-ки для дан

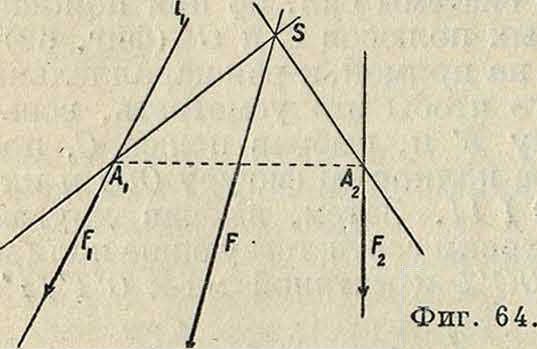
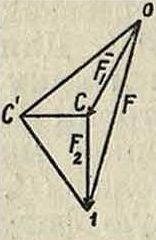
ной системы сил, соответствующие различным полюсам, расположенным на прямой, параллельной I. Последние выводы находят обширное применение не только в области графостатики, но и в др. областях, в теории шарнирных механизмов и тому подобное. Доказано, что все нитяные мн-ки для данной системы сил представляют собой ортогональные проекции на плоскость действия сил ломаных линий, полученных от сечения всевозможными плоскостями многогранника, ребра которого проектируются ортогонально на линии действия данных сил (Кремона, Клейн).

На основании вышеприведенных выводов можно решить графически ряд проблем, касающихся разложения данной силы на ее компоненты. Пусть требуется разложить данную силу F на две составляющие силы F_tn F_t так, чтобы линии действия последних проходили через две данные точки А_ги А ₂ (фигура 64). Взяв на линии действия силы F произвольную точку S и соединив ее с А_г и А ₂, можно разложить F на две компоненты по направлениям SAi и SA₃, величины и направления которых определяются сторонами ОС ж С1 соответствующей полярной фигуры. Если же кроме точек А_г и А₂ задано также и направление одной из компонент, например направление 1_г для первой силы, то, проведя через С прямую ССЦА₁А₂, а через 0 прямую ОС II 1_Х, получим, на основании предыдущих выводов, новую полярную фигуру 0С1, сторо---^ ----^

ны которой ОС и С1 определяют искомые силы F₁ и F₂. Пусть требуется разложить данную силу F (фигура 65) на три компоненты -Fj, F₂, F₃, лежащие в одной плоскости с F и линии действия которых 1_г, ϊ₂, 1_а даны. Обозначим линию действия F через I, а линию действия равнодействующей F₁₃первых двух сил F₁ и F₂ через ί₁₂. Допус-

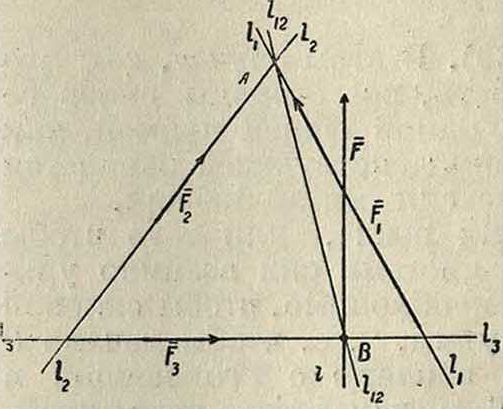
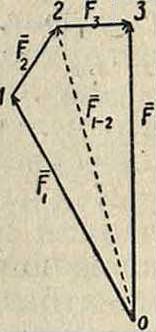
Фигура 65.

тим, что требуемое разложение произведено. Тогда, построив полярную фигуру для найденных компонент, придем к заключению, что, в виду свойства взаимной обратное™ фигур, тр-ку 012 соответствует точка А, в которой пересекаются прямые l_lt 1₂ и 1₁₂, а тр-ку 023—точка В, через которую проходят прямые ϊ₁₂. I и ?₃. Отсюда вытекает следующий способ построения: определив точку пересечения А прямых и ϊ₂ и точку пересечения В прямых I и 1₃, разложим данную силу F по направлениям АВ и 1₃, а затем разложим первую компоненту по направлениям и f₂.

Что касается пространственных систем сил, то графостатич. построения для них усложняются, причем во многих случаях эти построения комбинируют с методами начертательной геометрии (смотрите). Проще всего дело обстоит при наличии пространственной сходящейся системы сил, равнодействующая которых по величине и направлению равняется замыкающей стороне неплоского силового мн-ка и линия действия которой проходит через общую точку пересечения линий действия данных сил. Если спроектировать данные сходящиеся силы на две взаимно перпендикулярные плоскости, то в каждой из этих плоскостей равнодействующая проекций сил равняется проек-

ции равнодействующей силы. Обе равнодействующие проекции в ортогональных плоскостях и определяют равнодействующую в пространстве. Конкретно эти построения м. б. выполнены методами начертательной геометрии. Если имеется пространственная нссходящаяся система сил, то, взяв произвольную точку О, можно, как мы видели выше, перенести в эту точку все векторы сил, сохраняя их величину и направление и прибавляя при переносе каждого вектора соответствующий моментный вектор пары сил. Так как проекция моментного вектора каждой добавочной пары на какую-либо ось равняется моменту проекции переносимой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с плоскостью, то графически задача сводится к следующему. Спроектировав данную систему сил на три взаимно перпендикулярные плоскости и построив в каждой из них силовые и веревочные мн-ки для этих проекций, найдем три равнодействующие последних, определяющие равнодействующую силу в пространство. В то же время моменты равнодействующих сил, находящихся в плоскостях проекции, относительно точки пересечения плоскостей соответственно равны проекциям равнодействующего моментного вектора пар на взаимно перпендикулярные прямые, по которым пересекаются плоскости проекции. Зная же эти проекции, можно определить уже затем и положение равнодействующего моментного вектора пар, то есть положение равнодействующей пары в пространстве. Однако для определения положения в пространстве лишь вектора равнодействующей силы достаточно спроектировать систему сил на две взаимно перпендикулярные плоскости; для определения же положения моментного вектора равнодействующей пары необходимо спроектировать систему сил на три взаимно перпендикулярные плоскости. Можно применить еще и следующий графический метод приведения пространственной системы. Каждая из сил F данной системы может быть разложена на две компоненты, из которых одна F_s лежит в плоскости S, а другая F приложена к некоторой произвольной точке А, не лежащей в плоскости S (фигура 66). Для этого проведем через F и А плоскость, пересекающую плоскость £ по прямой Ϊ, и продолжим линию действия силы F до пересечения с ! в точке О. Переместив затем F в О, разложим ее на две компоненты: одну по направлению I, а другую по направлению О А. Первая компонента и дает нам силу F_s, а вторая, перемещенная вдоль О А в точку M, дает силу F. Точно так же можно поступить и со всеми остальными силами системы.

Для того чтобы разложить данную силу F на три сходящиеся компоненты F_lt F₂, F₃, не лежащие в одной плоскости и линии действия которых 1_и 1₂, 1₃ даны, можно применить следующий графический метод. Сначала определяется линия действия 1₁₂ равнодействующей F₁₂ сил F₁ и F₂ как прямая, по которой пересекаются плоскости (i₃,1₁₂) и (?!, ϋ₂). а затем разлагают силу F на компоненты F₃ и F₁₂, a F₁₂ на компонен ты J⁷! и F₂. Можно применить для этой же цели еще и следующий метод. Пусть сила F дана ее горизонтальной и вертикальной проекциями F и F" (фигура 67) и пусть направления 1_и 1₂, 1₃ также даны их горизонтальными и вертикальными проекциями

(К. ι.). (h> Ь), (Ц, i₃)·

Очевидно далее, что сила-F должна оказаться замыкающей стороной силового мн-ка сил F_lt Fz, F₃, точно так же как F" — замыкающей _{фиг 66}

стороной силового мн-ка сил Fi, FI, F₃, причем соответствующие вершины мн-ков должны лежать, по правилам начертательной геометрии, на перпендикулярах к оси 00. Направления проекций компонент F_x и F₃ определяются непосредственно прямыми (Ιί, Ιί) и (Ϊ3. II). Для определения же направлений F и F поступают след. обр. Проведя 12 1_г как предварительную проекцию F₃, находим предварительную же вертикальную проекцию 2 "2". Если переместить 12в положение 2 2 параллельно самой себе и притом таким образом, чтобы крайние точки остались на и is, то 1" 2" перейдет в положение 1"2", причем точка 2" будет перемещаться по не

которой прямой й. Следовательно, построив второй вспомогательный четырехугольник 2 ’ 1"2" 2 и соединив точки 2" и 2 прямой, определяем точку пересечения II" прямой d с Ц. Проведя затем ΓΊΙ" параллельно Ц, определим как силовой многоугольник ΟΓΊΓΊΙΙ", так и силовой многоугольник 0ΙΊΙΊ11 (метод Мюллера-Бреслау).

В последние годы, обобщая выводы графостатики плоских систем, создали стройную систему графостатич. методов для пространственных сист м сил (Мизес, Майор и др.). В основу пространственной графостатики положены следующие принципы. Пусть имеется сила F, компоненты которой по осям координат суть X, Y, Z. В плоскости хОу можно всегда найти такой вектор, проекции которого X, Y на оси координат равны компонентам X’ и Y и момент которого М относительно начала осей координат равен cZ, где с—некоторая постоянная величина. Т. о. имеется зависимость: Х=Х, Y=Y, cZ= Μ,

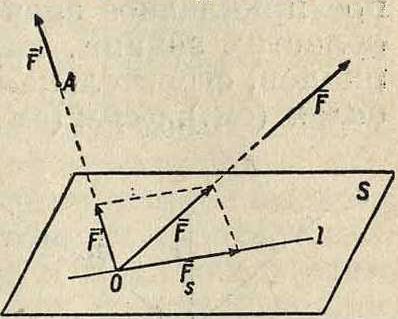
дающая возможность свести вопросы о сложении и разложении пространственных систем сил к сложению и разложению плоских систем.

Графостатические методы имеют громадное прикладное значение, особенно в таких областях знаний, как сопротивление материалов, строительная механика при расчете балок (смотрите), ферм (смотрите), мостов (смотрите) и т. д.

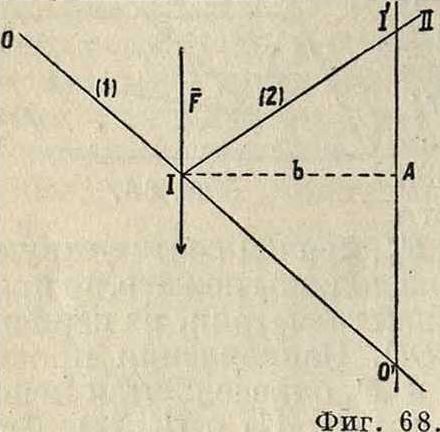
В основе этих расчетов графостатического характера лежат следующие положения. Допустим, что требуется определить момент силы F относительно данной точки А (фигура 68). Построив полярную фигуру и нитяной мн-к и продолжив стороны последнего до их пересечения в точках О и I с прямой, проведенной через А параллельно F, получим отрезок 0Ί, пропорциональный величине искомого момента. В самом деле: обозначая расстояние от точки А до F через b, а расстояние от С до 01 через h, имеем из подобия тр-ков I 1 О и 0С1:

i=44г-, или, т. к. 01=F, Ь -F=h Οϊ,

^п οι

что и показывает, что отрезок 0I пропорционален моменту bF, причем фактором пропорциональности является расстояние h. Если рассматривать величину h как силу, то получаем, что момент F относительно А равняется произведению величины силы h на отрезок 0Ί, причем h измеряется масштабом полярной фигуры, а 0Ί—масштабом основной фигуры. Если в частности принять h=1, то Fb=0I. Знак момента определяется стороной вращения F около А.

Пусть имеем в более общем случае плоскую систему сил F_lt F₂, F_n (фигура 69).

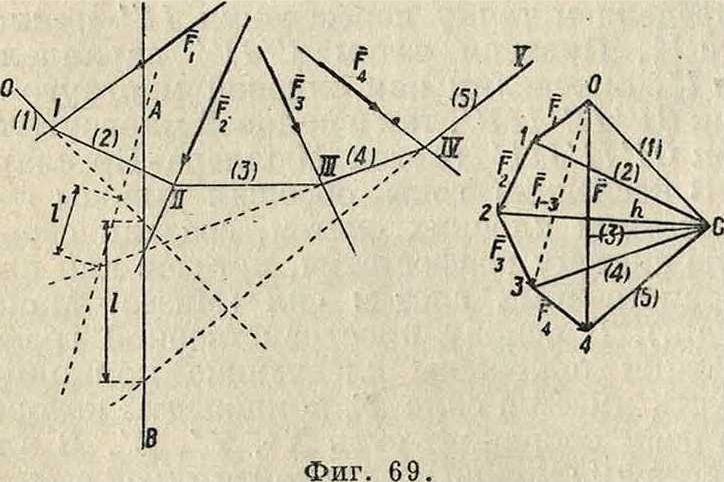
Так как алгебраич. сумма моментов сил составляющих, относительно какой-либо точки, равняется моменту равнодействующей силы относительно той же точки, то для того чтобы найти алгебраическую сумму моментов

I сил F_lt F₂, ., F_n относительно какой-либо точки А, достаточно построить при помощи силового и нитяного мн-ков равнодействующую F и найти выше приведен, графим, способом момент F относительно А, то есть продолжить крайние стороны нитяного мн-ка до их пересечения с прямой AB i! F и умножить получившийся так. обр. отрезок I на полюсное расстояние h. Очевидно, что, пользуясь этим методом, можно получить алгебраич. сумму моментов любой группы данных сил. Так например, для группы сил F_ltF₂, Fз достаточно провести через И прямую параллельную 03 полярной фигуры и найти точки пересечения ее со сторонами 01 и III IV. Получившийся отрезок Iумноженный на полюсное расстояние от С до 03, и дает алгебраическую сумму моментов рассматриваемой группы сил относительно точки А. Приведенные построения применимы очевидно и для системы параллельных сил; в этом случае расстояния от полюса С до всех сторон силового многоугольника между собою равны. О практических применениях указанных построений см. Балки простые, Фермы и др.

Графические построения при помощи силового и нитяного мн-ков применяются помимо того еще и во многих других случаях,

я

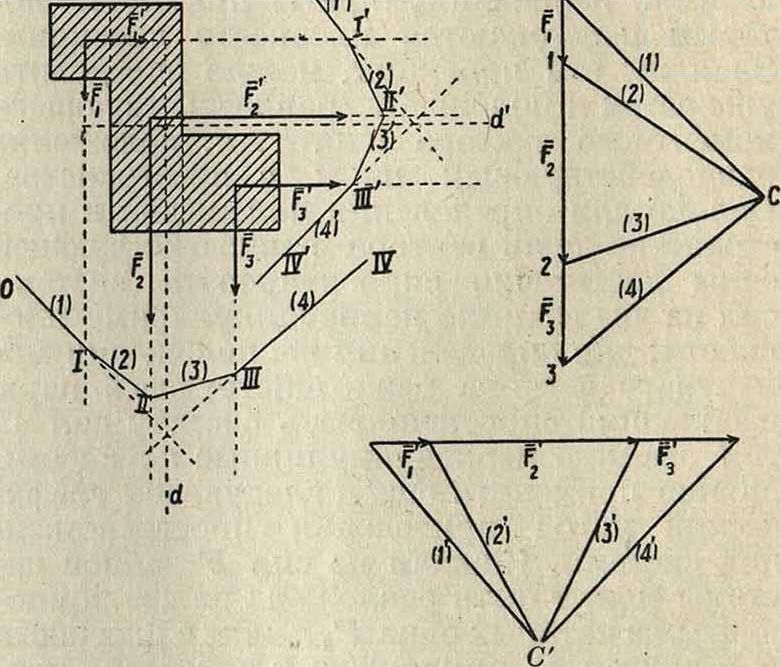
Фигура 70.

например для графического определения ц. т. плоских фигур, для определения распределения силы тока и напряжения в проводах, при графич. интегрировании диференциаль-ных ур-ий и т. д. Для графич. определения ц. т. однородной площади применяют следующий метод. Данную площадь разделяют на ряд таких частей, положения ц. т. которых известны либо точно либо приблизительно (фигура 70). Т. к. при однородности всей площади вес каждой ее части пропорционален площади последней, то, приложив к ц. т. частей параллельные векторы, пропорциональные соответствующим площадям, определяют при помощи нитяного и силового мн-ков линию действия d равнодействующей всех векторов. Повернув затем все векторы на один и тот же угол и сохраняя при этом неизменными величины их, построим аналогичным образом новую линию действия d равнодействующей повернутых векторов. Точка пересечения йийи определяет ц. т. всей площади.

Лит.: Жуковский Η. Е., Аналитич. механика, М.—Л., 1925; Ч а п л ы г и н С. А., Механика системы, ч. 1—2, М.—Л., 1923—24; Мещерский Ы. В., Курс теоретической механики, ч. 1— 2,М.—Л., 1927— 28; Бобылев Д, Руководство к курсу теоретик, механики, СПБ, 1895;СусловТ. К., Основы аналитической механики, 2 изд., ч. 1—3,Киев, 1911—12. Burin e s t e г L., Lehrbuch der Kinematik, Leipzig, 1886— 88; SchoenlliesA., Geometrie d. Bewegung in syn-thetischer Darstellung, Lpz., 1886; Sc hoeri flies A. u. G r ii b 1 e r M., Kinematik, «Enz. d. math. Wiss.», B. 4, T. 1, Abt. 1, H. 2, B.—Lpz., 1902; G r ii b 1 e r M., Lehrbuch d. technischen Mechanik, 2 Aufl., В. 1, B., 1921, B. 2, B., 1923; G r ii b 1 e r M„ Getriebelehre, Berlin, 1921; H eun K., Lehrbuch d. Mechanik, В. 1, Kinematik, Leipzig, 1906; Foppl

A., Vorlesungen liber technische Mechanik, В. 1—6,

B. —Lpz., 1921—27; P 6 s chi Tb., Lehrbuch der technischen Mechanik, 2 Aull., Berlin, 1930; Witt en-b a u e r l·., Graphische Dynamik, Berlin, 1923; Krause M., Analysis der ebenen Bewegung, Lpz., 1920; Study E., Geometrie der Dynamen, Leipzig, 1903; TimerdingH., Geometrie der Krafte, Lpz.—Berlin, 1908; Henneberg L., Die graphische Statik d. starren Systeme, 2 Aufl., Lpz.—B., 1911; Ball It., A Treatise on the Theory or Screws, Cambridge, 1900; Darboux &., MOmoire sur l’equilibre astatique, Bordeaux, 1877; Routh E. A., Treatise on Analytical Statics, v. 1—2, ed. 2, Cambridge, 1909; Routh E., Elementary Rigid Dynamics, L., 1892; Routh E., Die Dynamik d. System starrer Korper, В. 1—2, Leipzig, 1898; Cremona L., Le figure reciproche nella statica gralica, Milano, 1879; Mayer B., Statique graphique des syst6mes de l’espace, Lausanne, 1910; Mayer B., Statique graphique, Lausanne, 1926; Herzog J. und F e 1 d m a η n C., Die Be-reehnung elektr. Leitungsnetze in Theorie u. Praxis,

4 Aufl., B., 1927; Appel P., Traite de mdcanique rationnelle, t. 1—4, P., 1920—24; Charlier C., Die Mechanik d. Himmels, В. 1—2, Lpz., 1902—1907; Hamel G., Elementare Mechanik, 2 Auflage, Lpz., 1922; Lamb H., Higher Mecanics, Cambridge, 1920; Lamb H., Dynamics, 2 ed., Cambridge, 1923; Lorenz H., Lehrbuch d. techn. Physik, 2 Aufl.,B.l—2, Berlin, 1924—26; Love A., Theoretische Mechanik, B., 1920; Marcolongo R., Theoretische Mechanik, В. 1—2, Lpz., 1911—12; Muller C. und P r a n g e G., Allgemeine Mechanik, Hannover, 1923; Plank M., Eintuhrung in die allgemeine Mechanik,

4 Aufl., Lpz., 1928; Rausenberger O., Lehrbuch d. analyt. Mechanik, Lpz., 1888; Thomson W. a. Tait P., Treatise on Natural - Philosophy, Cambridge, 1879—83: Webster A., The Dynamics of Particles, 3 ed., Lpz., 1925; Whittaker E., Analyt. Dynamik d. Punkte u. starrer Korper, B., 1924; Cranz C., Lehrbuch d. Ballistik, B. 1—3, B., 1925—27; Gray A., A Treatise on Gyrostatics a. Rotational Motion, Theory a. Applications, L., 1918; Hagen J., La rotation de la terre, Roma, 1911; Poincare H., Les mOthodes nouvelles de la mfeca-nique celeste, t. 1—3, Paris, 1892—99; Klein F.u. Sommerfeld A., Ober die Theorie d. Kreisels, Η. 1—4, Lpz.—B., 1910—23; Grammel R., Der Kreisel, seine Theorie u. seine Anwendungen, Brschw., 1920; Tisserand F., Traith de mbcanique c61este, t. 1—4, P., 1889—96; Painlevi P., Legons sur le frottement, P-, 1895; Noether F., Die Bewegung einer rollenden Kugel, Mch., 1909; Fischer O., Theoretische Grundlagen f. eine Mechanik d. lebenden Korper, Lpz.—B., 1906; Thomson J., Applications of Dynamics to Physics a. Chemistry, L., 1886; Herz H., Die Prinzipien d. Mechanik in neuem Zusammenhang, 2 Aufl., Lpz., 1910; BolzmannL., Vorlesungen liber die Prinzipe d. Mechanik, T. 1—2, Lpz., 1922; Galilei G., Discorsi, Leiden, 1638; Huygens Ch., Horologium oscillatorium, P., 1673;. KulerL., Mechanica sive motus scientia,СПБ, 1736; Lagrange J., Mdcanique analytique, Paris, 1815; Laplace P., Mficanique celeste, P. 1805; Fou-caultL., Recueil des travaux scientifiques, P., 187 8; Poinsot L., Th6orie nouvelle de la rotation des corps, P., 1834; Poisson S., Traite de mecanique, 2 ed., P., 1833. -IVI. Серебренников.