> Техника, страница 62 > Модуль

Модуль

Модуль, термин, применяемый в сопротивлении материалов, теоретической физике, различных отделах математики, служит для обозначения особенно важных коэфи-циентов, чисел и совокупности определенных чисел.

В сопротивлении материалов встречается т. н. М. упругости, или М. линейного растяжения или сжатия (модуль Юнга). Пусть имеется брусок, на равные основания которого действуют равные, про тивоположные и равномерно распределенные по площадям оснований силы Р, и пусть будет далее длина бруска L, а площадь каждого из оснований s. Многочисленные опыты над растяжением и сжатием брусков различных материалов показали, что между так называемым растягивающим (с ж им а ю щ и м) напряжением и относительным удлинением (сжатием)

е=⁴^, (2)

где ΔΕ—удлинение (сжатие) бруска, существует следующая прямая пропорциональная зависимость:

1=Е, (3)

поскольку напряжения р не превышают известных пределов. Коэф-т пропорциональности Е и есть М. упругости (модуль Юнга). Из (1), (2) и"(3) следует, что

73 PL Е s AL ‘	(4)
При ΔL=L получаем из (4)
Е=-=р. S 1	(5)
Т. о. видно, что М. упругости	численно
равен такому растягивающему напряжению, при котором длина бруска удвоилась бы.
Величина
	(6)
называется коэфициентом	растя-
жения (сжатия). Модуль Е, определен-
ный вышеуказанным способом, относится к i	Р

V?

III!

р

Фигура 1.

изотермическому растяжению; при адиабатическом же растяжении получается другой модуль Е> Е (см.

Сопротивление материалов). Выделим мысленно в данной прак-тич. неограниченной среде призму ABCD (фигура 1), и пусть основания последней под-

р вергаются давлению р= —. Еслибы эта призма не была окружена со всех сторон данной средой, то длина ее стала бы равна на основании закона, выраженного ф-лою (4),

I=L - AL=L -f§=L (l —I) -1.(1 -ар). (7)

Но т. к. боковые стенки призмы будут подвергаться воздействию окружающей среды, мешающей призме свободно расширяться в стороны, то действительная длина I призмы будет больше той, которая определена формулой (7), а именно:

Г=L (l — —)=Ь (1 — ар). (8)

Т.к. Г>1, то из последнего равенства следует, что Е > Е. Величина Е называется М. о“д постороннего сжатия слоя, а

α= ~ — коэф-том одностороннего сжатия.

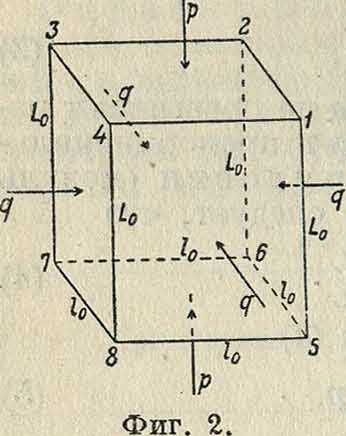
Между модулями ЕиЕ существует зависимость, к-рую можно установить след, образом. Допустим, что из рассматриваемого слоя вырезан прямоугольный параллелепипед 12.8 (фигура 2) с квадратным основанием, сторона которого равняется ϊ₀. Пусть далее на боковые поверхности призмы действует давление g, а на плоскости оснований—давление р, причем требуется, чтобы в результате всех этих давлений длина ребер 1₀ оставалась неизменной, а изменялась только длина боковых ребер L₀. Вследствие давлений р на плоскости оснований длина L₀ превращается в L₀ (1 — ар). Два боковых давления q, будуч ι приложены к граням 1265 и 3487, уменьшают длины 85, 76, 41 и 32 и увеличивают длину L₀, при этом каждая единица длины последней становится равной длине 1 + apq, где μ есть отношение относительного поперечного сжатия к относительному продольному растяжению (коэф-т Пуассона). Вследствие этого длина L₀ превращается в L₀(l — ар) (1 -f apq). Учитывая далее влияние давлений q на грани 1485 и 3267, получаем, что под одновременным воздействием всех давлений длина L₀ превратится в

Ι=£„(1-αρ)(1 + apqf, (9)

или с достаточной для практич. целей степенью точности

L=L_a [1 -ар (1 — 2 «-/()] · (10)

Сравнивая ф-лы (10) и (8), получаем:

α=α(ΐ-2^). (11)

Величина отношения Л определяется таким образом. Ребро 85 находится под воздействием следующих противоположных влияний, вследствие которых оно сохраняет свою величину. Давления q на грани 1265 и 3487 изменяют длину 1₀ в l₀(l—ад); давления q на грани 1584 и 2376 изменяют ее дополнительно в длину ϊ₀ (1 — ag) (1 + иад) и наконец давления р изменяют последнюю длину в ί₀ (1 — ag) (1 + рад) (1 + μαρ), причем в ре-зупьтате получается та же длина 1₀. Таким образом имеем:

ί₀=ϊ₀ (1 — ^аЧ) (1 + i«ag) (1 + μαρ),

или

1=(1 - ag) (1 + рад) (1 + μαρ), откуда почучаем с достаточной для практики степенью точности:

-q + pq + μρ=0,

или

ΐ _ μ ν 1-β

Подставляя значение (13) в (11), имеем:

(12)

(13)

или

1-μ-2μ² Χ-μ

Е=Е ;

, (1 +μ) (1—2/i)

ι-μ

(14)

(15)

(1 +#*) (1-2«) Следовательно между модулями Ε и E, с одной стороны, и между величинами а и а,

с другой, существуют для одного и того же материала определенные соотношения. Для нгопределенно большого слоя очевидно /(=0, так что в этом случае имеем из (15) и (14) E=Е и α= а. При μ=имеем: α= 0 и Е=оо.

Допустим, что поверхность нек-рого тела объёмом ν подвергается всестороннему сжатию, равномерно действующему на всю поверхность тела с давлением р. Опытным путем найдено, что изменение Ду объёма тела при малых деформациях прямо пропорционально величине объёма ν и давлению р, так что

Д ν=γ·ρν, (16)

где у—нек-рый коэф. пропорциональности, называемый коэф-т ом всестороннего сжатия; величина же К=— называет’ у ся М. всестороннего сжатия, или М. объёмной упругости тела. Между модулями К и Е существует следующая зависимость:

^к=(¹⁷>

При μ=I имеем К=Е.

Пусть имеются две параллельные плоскости АВ и CD, проведенные внутри какого-либо твердого тела (фигура 3), и пусть далее одна из плоскостей CD удерживается неподвижно, а другая плоскость АВ подвергается действию параллельных сил, лежащих в этой же плоскости и равномерно распределенных по ней, вследствие чего плоскость АВ сдвинется по отношению к-шгоскости CD, приняв положение АВ. Проведем плоскость ELMN, перпендикулярную как к плоскости АВ, так и к действующим в ней силам. После сдвига плоскости АВ плоскость KLMN примет положение KLMN, образовав с предыдущей двугранный угол у, называемый углом сдвига. Как показывает опыт, угол сдвига у прямо · пропорционален действующей силе р, приходящейся на единицу площади АВ, так что у=пр, (18)

где п есть нек-рый фактор пропорциональности, называемый коэфициентом сдвига. Величина G=— называется М. сдвига, так что у=или р=Gy. (19)

Из (19) видно, что при у=1, G=р, т. e. М. сдвига равен такому напряжению, под действием которого угол сдвига был бы равен единице, то есть одному радиану, если бы значительно ранее этого не были достигнуты предел упругости тела и затем разрушение последнего. Между модулями G и Е существует следующее соотношение:

^G=2irb·

		1W7,
А А	К
	у

Фигура 3.

Пусть имеется цилиндрич. стержень, одно основание которого закреплено, а другое подвергается действию пары сил, лежащей в этой же плоскости, и момент которой равен М (крутящий момент М). Под действием этой пары свободный конец стержня будет закручен на некоторый угол φ. Как установлено опытным путем, угол закручивания φ пропорционален моменту М вращающей пары, длине Ϊ стержня и обратно пропорционален четвертой степени радиуса г основания стержня (закон Кулона), так что п Ml

<Р=С-^,

(21)

где С—нек-рая постоянная, зависящая от

Cl

вещзства стержня. Обозначая ~ через к, имеем:

<р=кМ, (22)

где к есть т. н. коэфициент кручения. Величина /, обратная к, называется М. кручения, так что:

/=т =

Ii

Cl

(23)

M=f<p. (24)

^г Между М. кручения и М. сдвига G существует зависимость, к-рую можно установить следующим образом. Пусть имеем отрезок стержня с произвольным сечением и осью 00 (фигура 4) и допустим, что нижнее основание повернулось в своей плоскости на угол φ по отношению к верхнему основанию, причем элемент ds нижней пло-> скости повернулся около центра О на такой же угол φ. Проведя через начальное положение В элемента ds нормаль к верхней плоскости, найдем в ней положение *4 соответствующего элемента площади. После поворота нижнего основания прямая АВ превращается в винтовую линию А С, причем угол между ней и образующей ВАС=у характеризует угол сдвига. Развернув тр-к ВАС на плоскость, получаем:

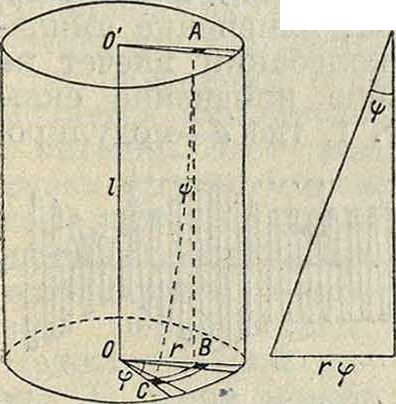
Фигура 4.

tg v> =

Τφ

(25)

где r—расстояние от элемента плоскости до центра О, а I—длина оси 00. Вследствие обычной малости угла у> можно вместо (25) написать

V-т· (26)

Для того чтобы вызвать угол сдвига, равный ν, необходимо, как мы видели выше, приложить к единице площади силу Gy>, или к элементу ds силу ΰψ ds, причем момент последней силы относительно оси 00 очевидно равен Gyirds или на основании (26)

γ as. Откуда имеем, что момент М вращающей пары равен

M=^Jr²ds, (27)

где интегрирование распространяется на всю площадь основания. Обозначив — через f, имеем из (27) окончательно:

f=jf г² ds. (28)

Для различных сечений значение интеграла в правой части (28) различно. Так, для круглого сечения радиуса R имеем, введя полярные координаты со и г,

2π R

Jr² ds =J J r² r deo dr=^π-- ·

ffl=0r=0

В этом случае имеем:

, _ nGR*

2 Г"

(29)

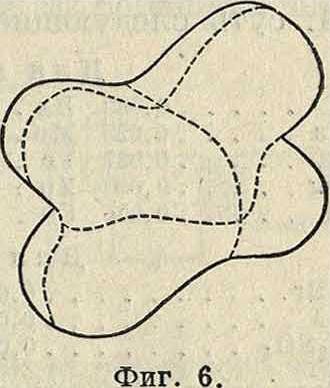
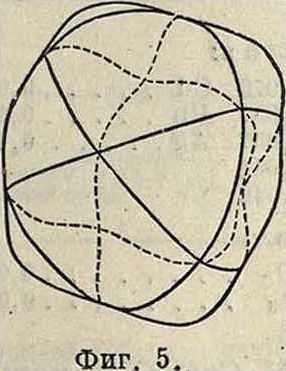
Из сопоставления всех вышеприведенных определений для коэф-тОв и М. явствует, что коэф. определяет всегда величину деформации, соответствующую напряжению, равному единице, а модуль определяет, наоборот, величину напряжения, которое способно вызвать деформацию, равную единице. Изотропные тела имеют два М., через которые все остальные М. могут быть выражены, например через К и G. Кристаллические, или анизотропные тела различных систем имеют, в зависимости от направления деформации по отношению к главным осям упругости (смотрите Упругость), непрерывно изменяющиеся по величине значения одного и того же М. Если отложить из какой-либо точки тела отрезки, пропорциональные модулю Е для тех же направлений, то геометрии, место концов этих отрезков образует т. н. п о-верхность М. растяжения. По виду этих поверхностей кристаллы распадаются на 9 классов. На фигуре 5 и 6 представлены поверхности М. растяжения для плавикового шпата, принадлежащего к правильной системе, и для барита, принадлежащего к ром-бич. системе.

В различных отделах математики термину «модуль» придается различный смысл. В математич. анализе М. называют чаще всего абсолютное или арифметич. значение какого-либо алгебраического числа или ф-ии. В векторном исчислении М. или абсолютной величиной вектора называется

числовое значение F данной векторной величины F, так что вектор F равен модулю F, умноженному на соответствующий единичный вектор F°, т. e.F=F-F> (смотрите Векторное исчисление). М. комплексного числа а + Ьг называется выражение ] а² + Ь²=ρ. Если данное комплексное число представить графически, отложив по оси абсцисс прямоугольной системы координат («ось дейст-

вительных чисел») отрезок, равный а, а по оси ординат («ось мнимых чисел») отрезок, равный 6, то комплексное число будет пред-ставленс некоторою точкою М, расстояние которой дс начала О осей координат очевидно и равняется М. комплексного числа. Угол <р, образованный прямою ОМ с осью X, называется амплитудою комплексного числа. Так как

α= ρ cos φ; b — q sin ψ, (30)

то

a+6i=ρ(οοβ ?> + tsmy). (31) Из вышесказанного следует: 1) М. комплексного числа есть всегда число положительное, за исключением того случая, когда <х=0 и 6=0; 2) М. суммы нескольких слагаемых комплексных чисел не более суммы М. слагаемых; 3) М. разности двух комплексных чисел не больше суммы М. уменьшаемого и вычитаемого и не меньше их разности. В теории чисел М. называется всякая совокупность чисел, обладающая тем свойством, что сумма или разность двух произвольных чисел совокупности принадлежит к той же совокупности. Нетрудно усмотреть, что всякий Μ.: 1) содержит число нуль, 2) содержит как положительные, так и отрицательные числа и 3) состоит из совокупности чисел, кратных наименьшего положительного числа М. Так например, совокупность четных чисел. —6, —4, —2, 0, + 2, +4, +6,. есть М. Равно совокупность всех целых чисел есть также М. Представителем М. очевидно является наименьшее положительное число из совокупности, и его для краткости можно назвать «модулем». Напр. «модуль 5» обозначает совокупность чисел. — Ϊ0, —5, 0, +5, +10,. Если разность а— 6 двух чисел а и 6 принадлежит к модулю т (другими словами, а—6 делится на тонн), то говорят «а сравнимо с 6 по модулю т» и выражают это так:

а= 6 (mod. тонн).

Понятие М. имеет для теории чисел фундаментальное значение (смотрите Теория чисел).

В теории растворовМ. называются числа, характерные для каждого металла и к-ты, которые следует прибавить к числу 1,015, представляющему плотность Vi-Ν’ NH₄C1, чтобы получить плотность данного Vi-N. Эти М. суть следующие:

Для металлов:

К.о,озо Ва. 0,073 cd.ο,οβι

Na. 0,025 Μη. 0,037 Рb.0,103

Са. 0,027 Fe. 0,037 Ag.0,105

Mg. 0,020 Zn.0,041

Sr. 0,055 Cu.0,042

Для кислот:

НВг. 0,034 HN0₃. 0,015

HJ.. 0,064 НСОз.0,014

H₂S0₄.0,020

Так например плотность Vi N Ca(N0₃)₂ равна

1,015+0,027+0,015=1,057.

В машиностроении М.—величина т=D:z, где Ώ—диам. начальной окружности зубчатого колеса в миллиметров, а г—число его зубцов.

Лит.: Бобылев Д., Гидростатика и теория упругости, СПБ, 1886;×в о л ь с о н О., Курс физики, т. 1, Берлин, 1923 (с обширной библиогр.); Млодзеевский Б., Основы высшей алгебры, М.—П., 1923; Егоров Д., Элементы теории чисел, Μ.—П., 1923; Clebsch A., Theorie d. Elastizitat festen Korper, Lpz., 1862; Gras hoi F., Theorie

d. Elastizitat u. Festigkeit, В., 1878; Lami G., Legon sur ia theorie mathdmatique de i’elasticitd des-corps solides, Paris, 1890; Math i eu E. Thdorie de 1’eiasticite des corps solides, Paris, 1890; Neumann F., Vorlesungen liber die Theorie d,Elastizitat d. festen Кбгрег u. Lichtathers, Lpz., 1885; Young Th., Course of Lectures on Natural Philosophy, L., 1807; S a i n t-V e n a n t, Torsion des prismes, P., 1855; Voigt W., Lehrbuch d. Kristallphisik, Lpz., 1928; Humbert G., Cours d’Analyse professe a l’Ecole polytechnique, v. 1—2, P., 1903—04. IY1. Серебренников.