> Техника, страница 62 > Момент

Момент

Момент, в широком обобщенном смысле произведение двух величин различных физических размерностей, причем одна из этих величин является длиной или степенью длины. Если вторая величина м. б. разбита на элементы, то М. составляется из суммы отдельных элементарных М. Первая величина—длина—геометрически изображается отрезком, вторая—либо точкой либо направленным отрезком. Обычно наименование М. относят к этой второй величине, то есть говорят о моменте этой второй величины. При вычислении М., а также при геометрии, изображении его, всегда ориентируются или относительно какой-нибудь определенной точки (полюс, центр М.) или относительно прямой (ось), иногда относительно плоскости. М. придают либо только -О численное значение (существенно положительный М.) либо приписывают кроме того и знак плюс или минус. Пусть один множитель произведения, составляющего М., выражается направленным отрезком, то есть вектором А (фигура 1); задаемся точкой О в качестве полюса. Численное значение для М. вектора-i будет произведение A-d, где d—длина перпендикуляра из точки О на направление вектора А (d—длина, о которой говорится в определении момента). Меняя направление вектора А на противоположное, мы согласно определению получим то же самое численное значение для М. Между тем в практич. вопросах желательно различать эти два случая. Для этой цели приписывают М. в одном случае знак плюс, а в другом минус (в каком случае плюс и в каком минус—зависит от условия), например исходя из следующего соображения. Воображая плоскость через данный вектор А и точку О, укрепленную в полюсе О, вращают эту плоскость по направлению вектора вокруг точки О; если вращение происходит по движению часовой стрелки, то М. приписывают знак плюс, в противном случае—знак минус. В этом условии имеется неопределенность: одно и то же вращение будет казаться происходящим и по движению часовой стрелки и против, в зависимости от расположения наблюдателя над или под плоскостью вращения. Однако при постоянстве места наб

Фигура 1.

людателя два различных вращения всегда будут отмечены разными знаками у М., чего в сущности и достаточно. Впрочем эту неопределенность легко устранить введением понятия о лицевой стороне и изнанке плоскости или изображая момент вектором, перпендикулярным плоскости, проходящей через данный вектор А и точку О, и условившись направлять вектор М. согласно правилу штопора.

В интерпретации векторного исчисления (смотрите) момент Ш вектора А относительно полюса О можно представить в виде векторного произведения

М=[гА],

где г—радиус-вектор начальной точки данного вектора А относительно точки О.

Отнесем данный вектор А к произвольной прямой I, принимаемой за ось М. Для построения и вычисления М. вектора А относительно оси ί поступают след. обр. Проводят плоскость S перпендикулярно к оси I: пусть точка пересечения плоскости с осью будет О; проектируют данный вектор А на эту плоскость S и определяют М. проекции вектора А на плоскость S относительно полюса О; этот М. и называют М. вектора А относительно оси. Д. Колянковсний.

М. инерции плоских фигур. При изучении изгиба, кручения, в задачахгидростатики приходится встречаться с М. инерции плоских фигур. Осевым, или э к в ат о р.и а л ь-н ын, М. инерции плоской фигуры относительно оси ОХ, лежащей в ее ₀плоскости, (фигура 2), называется предел суммы произведений из элементарных площадок deo этой фигуры на квадрат расстояний их

« от оси ОХ:

^J с

I_x=jy²dco, (1)

(ш)

где интегрирование распространено по всей площади а). Подобным же образом относительно оси OY:

Ir⁼ f ^χ2 dm. (2)

<»)

Полярным М. инерции этой же фигуры относительно точки О называется

Io-ffd со, (3)

(ш)

где г—расстояние элемента deo от точки О. Ясно, что

Ι₀=Ιχ + Ιγ· (4)

Центробежным М. инерции относительно двух осей ОХ и ΟΥ называется

(5)

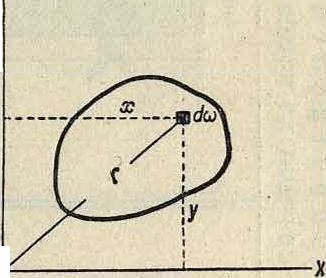
Фигура 2.

_r=Jxy d(0.

(со)

Размерность всех этих величин—[длина]⁴. М. инерции всегда положительны и отличны от 0; центробежный момент м. б. положительным, отрицательным или же нулем. Если точка О совпадает с ц. т. С плоской фигу- ры (фигура 3), то соответственные М. инерции

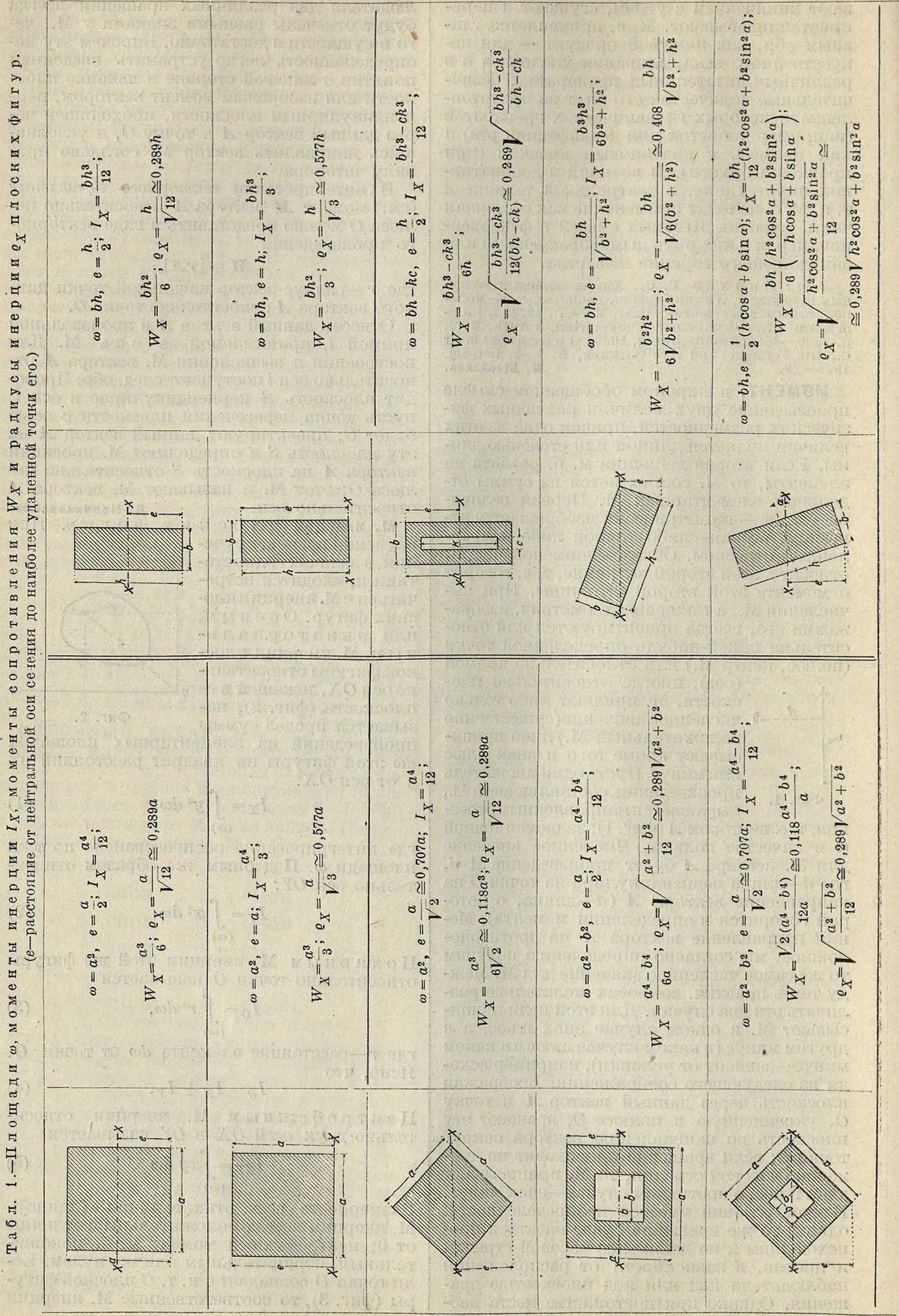
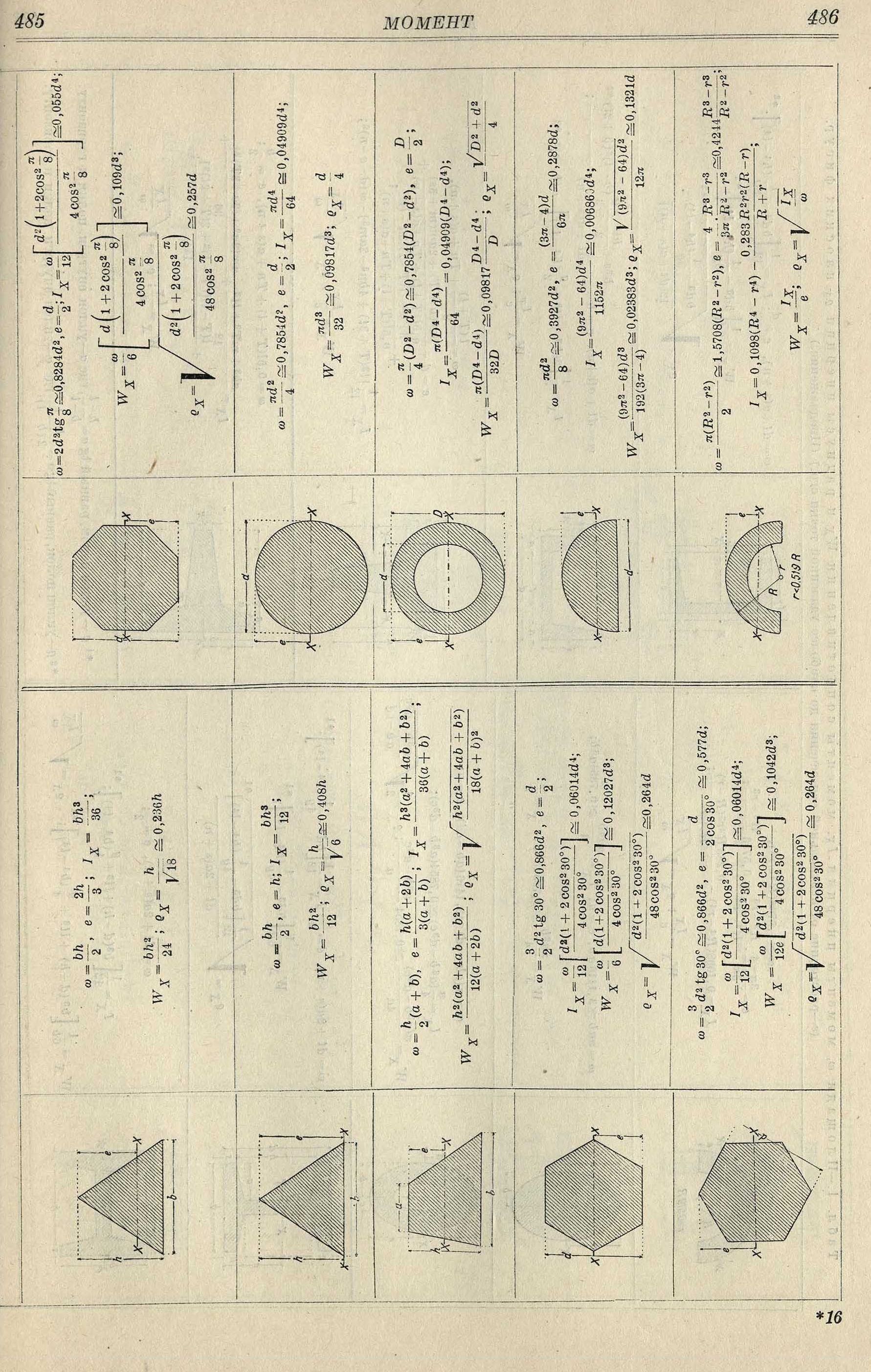
(е—расстояпие от нейтральной оси сечения до наиболее удаленной точки его.) (Продолжение.)

2д—уклоп полок, равный tga= ——— где а—уклоп внутрен. полки к горизонту.

Μ.

называются центральными моментами Ι_χΰ, 1у_С и 1₀с М. инерции Ι_σ относительно осей EU и EV, параллельных осям СХ и CY и находящихся от них на расстояниях а и Ь: 2ц= 4-хс + cob², Ιγ= Iyc + аза². (6) Полярный М. инерции относительно точки Е: Ιϋ=4_οα + ω1³, (7)

где 1ос—полярный М. инерции относительно ц. т. С. Из (6) и (7) видно, что М. инерции относительно ц. т. являются наименьшими. Центробежный момент 1_иг относительно новых осей EV и EU, параллельных прежним CY и СХ на расстояниях а и Ь:

Iυν — 4ху(оаb. (8)

М. инерции относительно оси ОЛ, составляющей угол а с осью ОХ:

I_a=I_xcos² а + iysin² а — I_xysin 2α. (9) Если выберем угол а так, чтобы

tg 2 α =

_2ΐχτ_

Iy-Ιχ’

(10)

то получим два взаимно перпендикулярных направления О А и ОБ, для которых центробежный М. инерции 1_АВ=0, а М. инерции до

стигают наибольшего и наименьшего значений I₁n 1₂. Эти оси называются главными осями, а 1₁ и 1₂ — главными М. инерции.

Л- ~ dx + Ir) +1 - It? + 4T г)

Для любых осей

2α= li cos² а + /„sin² а. (12)

Главные оси, проходящие через ц. т. С, называются главными центральными осями инерции, а моменты относительно них—г л а в н ы м и центральными М. инерции. При наличии в контуре фигуры оси симметрии последняя является одной из главных осей. Длина ρ =l/"называется радиусом инерции площади ω относительно оси Оа. Если по направлению луча Оа откладывать отрезки, обратно пропорциональные длине соответственного ρ, то концы этих отрезков при вращении Оа около точки О расположатся по так называемым эллипсу инерции, ур-ие которого 2if² + lpf·=Const;

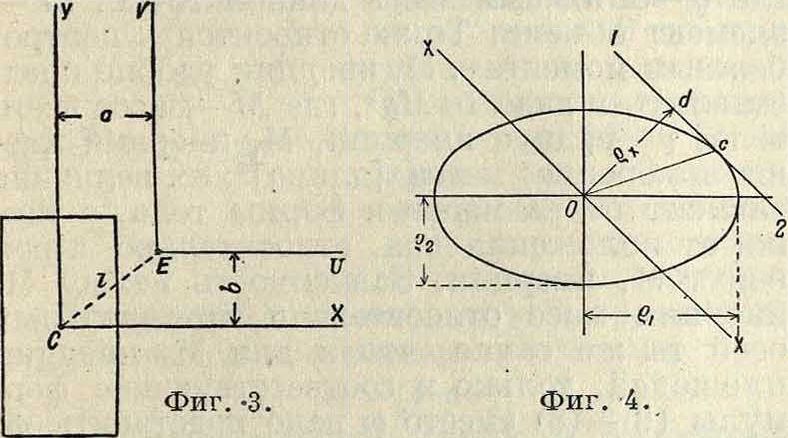
его оси совпадают с главными осями инерции плоской фигуры. Эллипс инерции дает наглядную картину изменений М. инерции при повороте осей около точки О. Если отложить на главных осях отрезки ρι и ρ₂

по направлению, перпендикулярному к оси (фигура 4), и на этих отрезках построить эллипс, то он будет подобен первому эллипсу и называется вторым эллипсом инерции (Кульмана). По этому эллипсу инерции М. инерции относительно любой оси определяется выражением вида

IX *—— ωρ^_=cood²,

где od—расстояние от ц. т. эллипса до касательной, проведенной параллельно оси ОХ. Центробежный М. инерции определяется произведением Ι_ΧΥ=ω od ос. М. инерции для. правильных фигур и для фигур, составленных из правильных, вычисляется по ф-лам (1) — (5). Для неправильных фигур применяется следующий вычислительный прием:, площадь данной фигуры разделяют рядок прямых, параллельных оси ОХ, на полоски настолько узкие, чтобы их можно было рассматривать как прямоугольники. Определяют по чертежу площадь каждой полоски а>_г, со₂,. и расстояние у ее ц. т. от оси ОХ. Тогда приближенно

Ιχ-ΣΚ+ΐτ)· · ⁽¹³>

Вторым членом при малой ширине полоски h можно пренебрегать. При графич. определении М. инерции фигуры (фигура 5, а) величины в)_1; ω₂,. изображают в виде векторов, приложенных в ц. т. каждой полоски, строят для них силовой мн-к (фигура 5, б) с полюсным расстоянием Н и по нему веревочный мн-к (фигура 5, в), продолжая стороны его до пересечения с осью Х-ов; приняв затем полученные на оси Х-ов отрезки за силы, приложенные в ц. т. указанных полосок, строят для них второйсиловой мн-к (фигура 5, г) с полюсным расстоянием Н₁ и по нему строят второй веревочный мн-к (фигура 5, д), продолжая стороны его до пересечения с осью Х-ов.

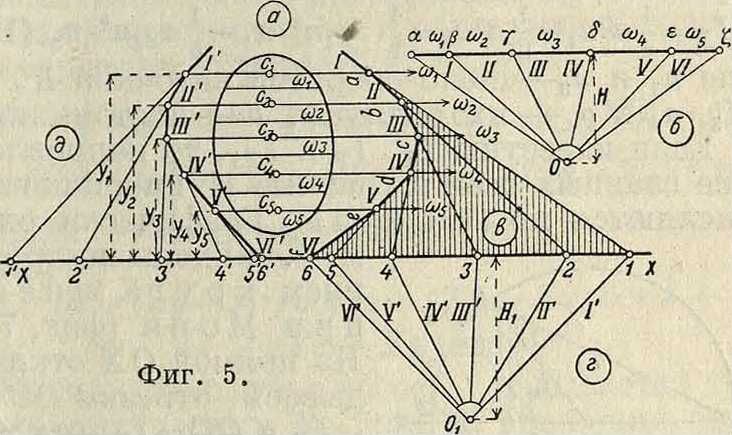
По этим построениям момент инерции 1_Х определяется приближенно следующими выражениями:

1_Х= Тб Н Н — 2со_е · Н, (14) в к-рых: 16—отрезок, отсекаемый крайними сторонами второго веревочного мн-ка на оси Х-ов; ω„—площадь, ограничиваемая крайними сторонами первого веревочного мн-ка и осью Х-ов. Можно также для вычисления М. инерции пользоваться интеграторами. На фигуре 6 показана схема интегратора Амслера. При определении М. инерции фигуры относительно оси XX устанавливают прибор так, чтобы линейка SS была параллельна оси XX; для этого служат две линейки Р и Т равной длины, снабженные на одном конце поперечиной, входящей в паз линейки SS, а на другом—острием, которое устанавливают на ось XX. При обводе штифтом, насаженным на конце В стер-

ψ ^	sfi!
Т V 4 ) 4	Щ р 34 <
X А ХА	Щ в Ж2

Фигура 6.

жня АВ длиною, равною а, контура фигуры (например рельса) каточек К _х совершает нек-рый путь качения и_х=J sin φ· dx. Каточки К₂

и К₃ в то же время совершают качения м₂ и и₃, величины которых согласно устройству прибора будут:

щ=J·sin (90° — 2<р) dx и м₃=I sin 2>ψ dx.

Зная число оборотов каточков К_х, К₂ “ -Кз и радиусы их, можно вычислить величины и_х, м₂ и и₃; это вычисление заменяется делениями, наносимыми на каточках в соответствующих масштабах в зависимости от конструкции прибора. Величина М. инерции определяется выражением:

Ιχ— ^а?и_х—~а?и₃= i щ_ха?-п_х— *πρ₃α³·η₃,(15)

где п_х и «з—число оборотов каточков К_х и К₃, ρ_χ и ρ₃ — их радиусы, а — постоянная.

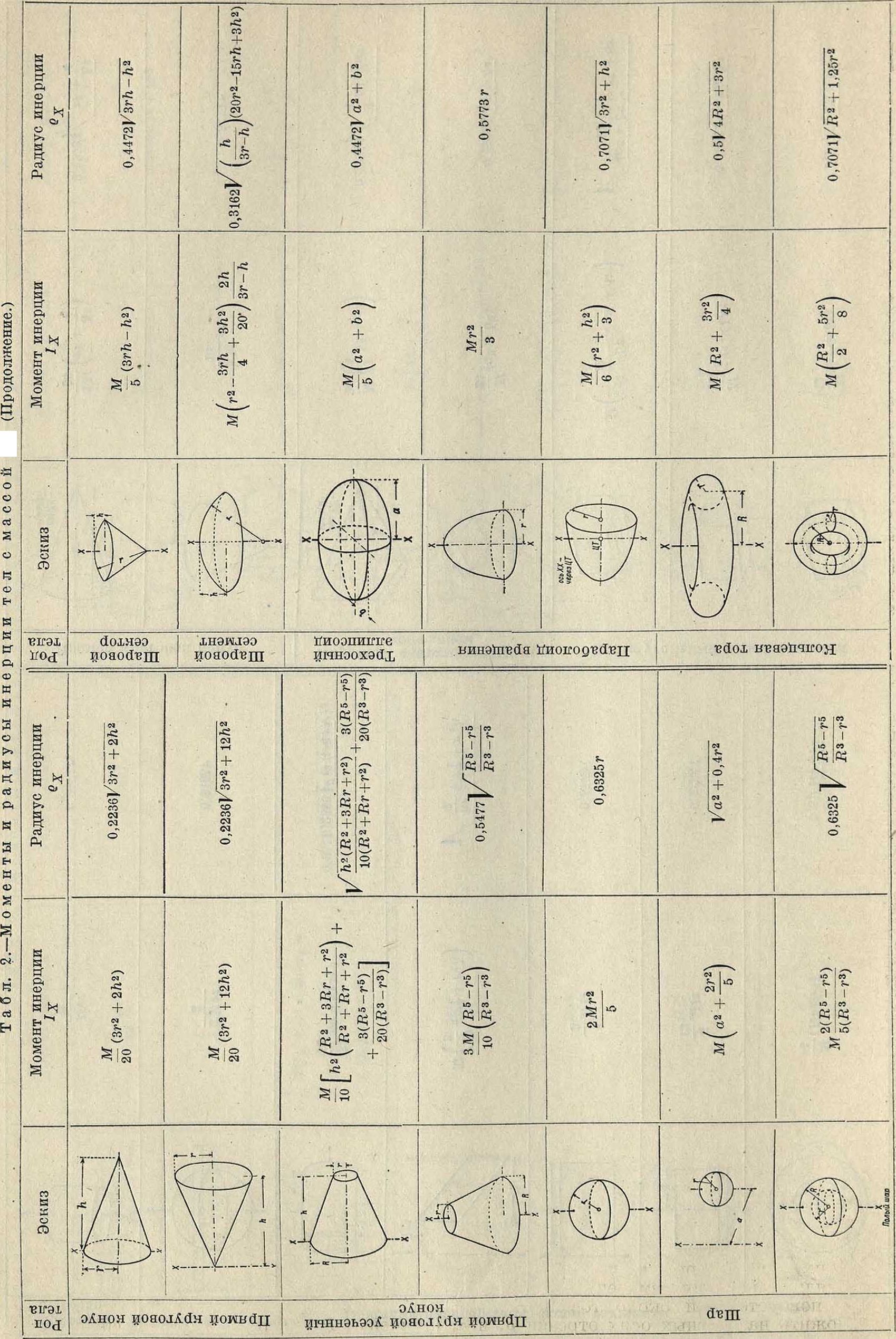
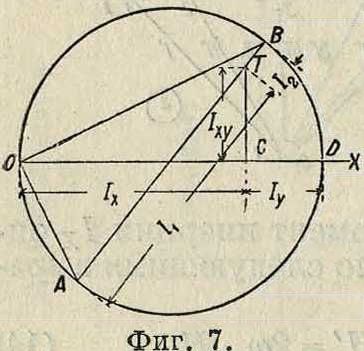
Если известны Ι_χ, ϊ_γ и 1_ΧΥ, то направление главных осей и главные М. инерции вычисляются πό (10) и (11). Графически они м. б. найдены построением круга инерции Мора (фигура 7). На прямой ОХ откладываем отрезки ОС== 1_Х и CD=Iy, откладываем СТ=1_Ху перпендикулярно к OD в положительную или в отрицательную сторону в зависимости от знака Ι_Χγ. Точка Т называется главной точкой и н е р-ц и и. Строим на OD как на диаметре круг. Проводим через Т диаметр НТВ. Линии О А и ОВ дают направление главных осей, а от резки АТ=1_пшх и ВТ=I_min—величины главных моментов инерции. М. инерции для различных плоских фигур даны в таблице 1.

М. инерции масс. В ур-иях и законах динамики, относящихся к вращению тел, вместо массы тела входит М. инерции его массы. М. инерции материальной точки от носительно оси ОА называется произведение из массы точки ж на квадрат расстояния ее от оси О А:

I=mr². (16)

М. инерции системы точек называется сумма произведений из массы каждой точки на квадрат ее расстояния от оси

z=2^mr2· (¹⁷)

М. инерции относительно системы трех взаимно перпендикулярных осей OXYZ:

ι_ζ= 2^т(^ж2 + ^)· с^)

Центробежными М. инерции, или произведениями инерции относительно координатных плоскостей, называются суммы

1_хг=^тху, I_xz=^mxz, 1_Т2=^туг. (19)

Если массы сплошь заполняют данный объём, то суммирование заменяется интегрированием по объёму:

I - J г² dm=-_д J qr² dV, (20)

где q—объёмный вес в данной точке, dV— элемент объёма. То же относится к центробежным моментам. М. инерции удобно представлять в виде Ι=Μρ², где М—масса всего тела, ρ—радиус инерции. М. инерции имеют измерение: масса [длина]²; их величина зависит от размеров и формы тела, а также от положения оси, относительно которой берут М. инерции. Зависимость между М. инерции масс относительно параллельных осей та же самая, что и для М. инерции площадей, только в соответствующие формулы (6)—(8) вместо со надо подставить т. М. инерции для оси О А, образующей с осями координат углы а, β, у:

Ι_Α=I_x cos² а + I_r cos² β + Iz cos² у —

— 2 Ι_Χγ cos a cos β — 21 ух cos β cosy —

— 2 I_Xz cos a cosy. (21)

Для каждой точки тела существуют 3 взаимно перпендикулярных оси, для которых центробежные моменты Ι_ΧΥ= 1χζ=Ιγζ=0. Эти 3 оси называются главными осями, М. инерции относительно их—главными М. инерции; их обозначим через А, В, С. Если тело имеет плоскость симметрии, то каждая прямая, перпендикулярная к ней, является главной осью. Если тело имеет ось симметрии, то эта ось является одной из главных осей инерции. Если по оси О А отложить от начала координат отрезок, пропорциональный, то концы его будут лежать на поверхности эллипсоида инерции

Αξ* + Βη* + Οζ*= 1; (22)

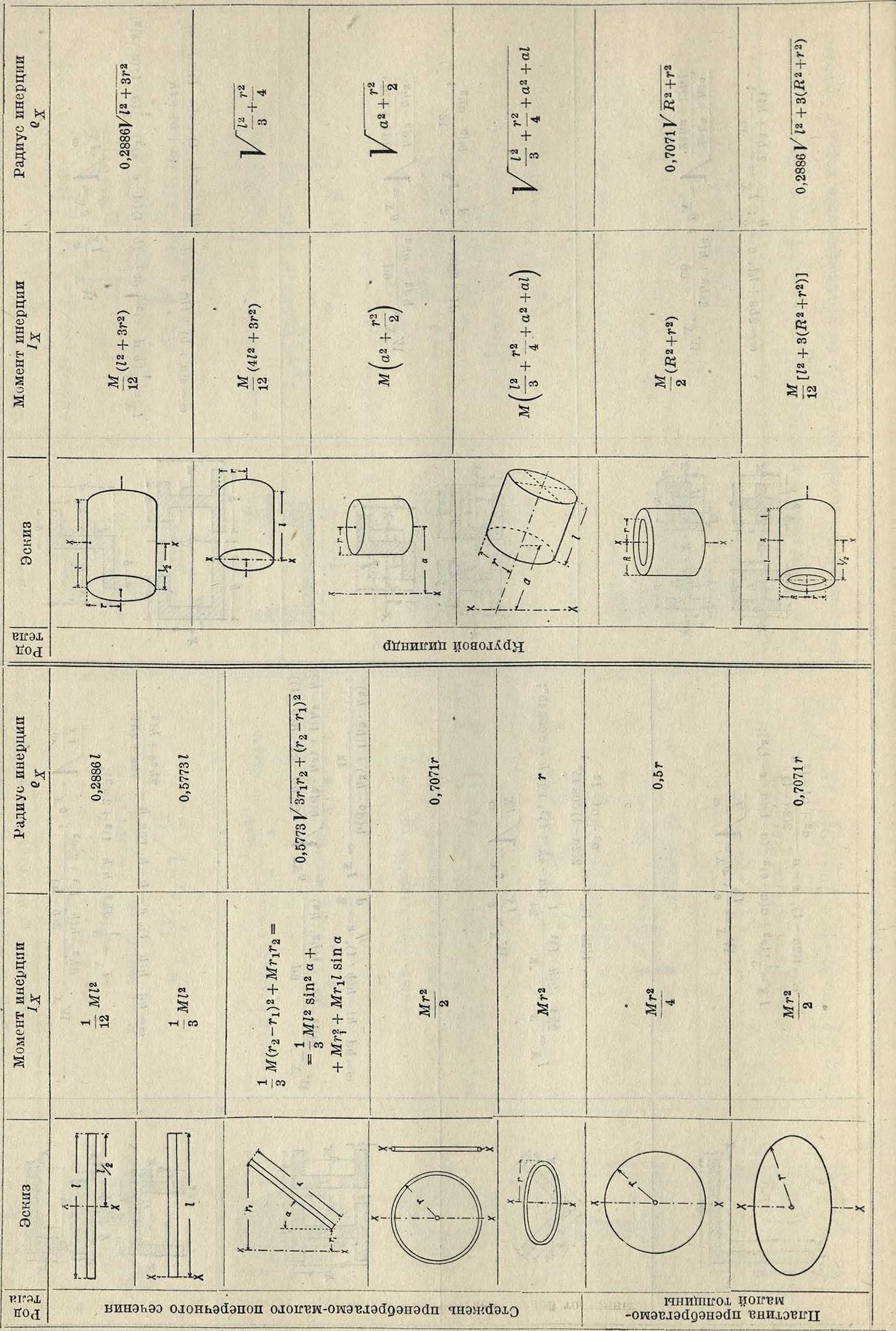
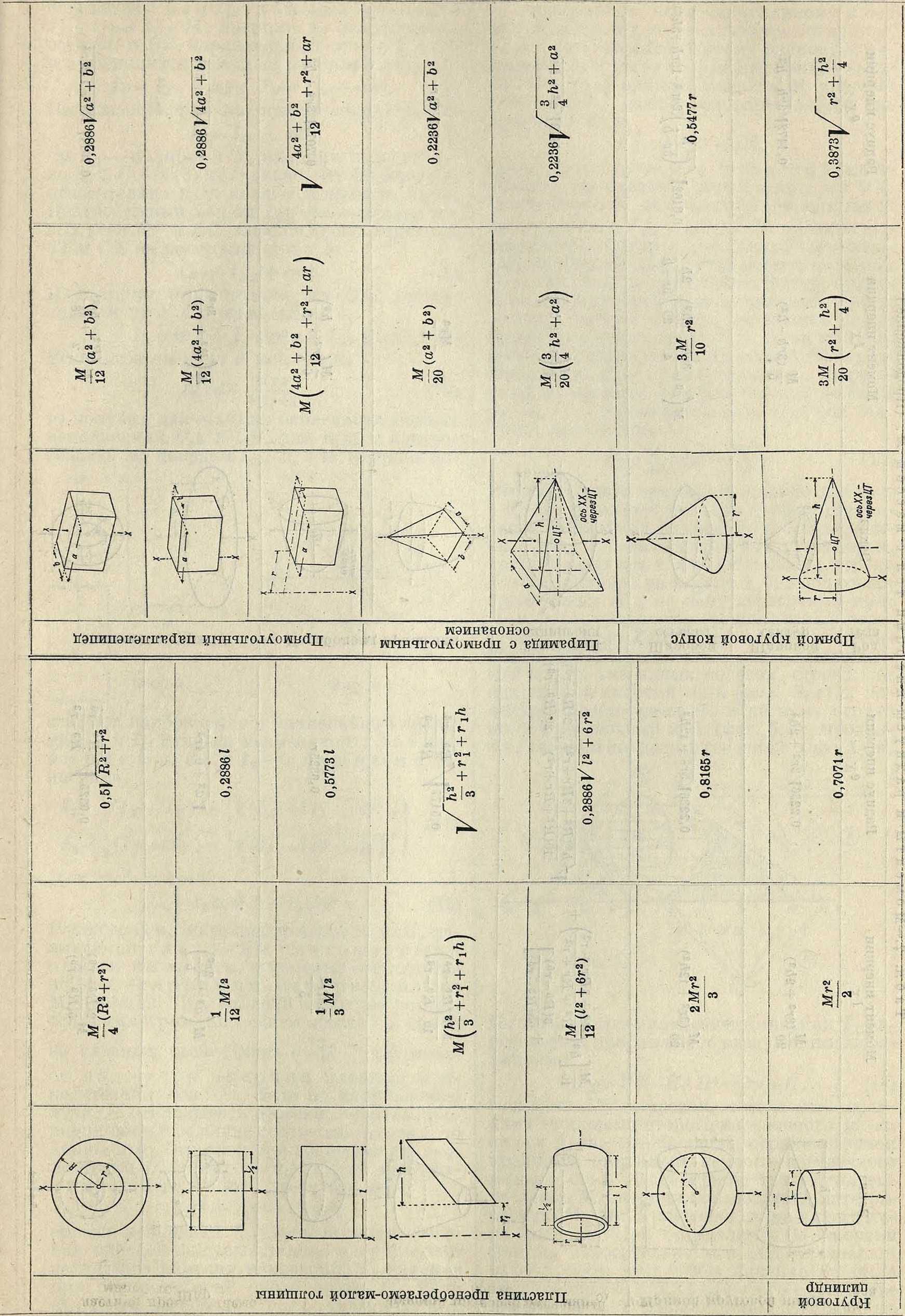
оси его совпадают с главными осями инерции. Приводим в таблице 2 главные центральные М. инерции для различных однородных тел с массой М.

Существует ряд способов для определения I на опыте. Например подвешивают тело и заставляют его совершать под действием силы веса малые колебания; пусть период этих колебаний ί₀; затем прикрепляют к нему другое тело, центр тяжести которого со-

впадает с оеыо вращения, с известным М. инерции 1₀; снова определяют период колебаний 1_г. Молено показать, что

i 1_и :^i;. · ti -ц

М. инерции элемента объёма относительно оси ОА называется произведение объёма этого элемента dV на квадрат его расстояния от оси О А, то есть г² dV. М. инерции о.бъема какого-либо геометрич. тела относительно оси ОА называется предел суммы произведений из элементарных объёмов этого тела на квадрат расстояния их от оси:

I=lim 2^r2 dV=fr*dV,

где интегрирование распространено по всему объёму тела. Подробности смотрите выше— М. инерции масс.

Лит.: Handb. d. physik. u. techn. Mechanik, hrsg. y. F. Auerbach u. W. Hort, В. 1, p. 350—404, Lpz., 1928: H ti 11 e, Справочная книга для инженеров, 12 изд., т. 1, стр. 244—250, М., 1929. А. Д инник.

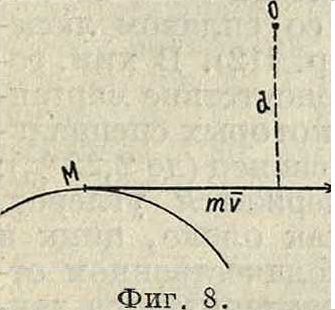
М. количества движения материальной точки М с массой т и со скоростью υ относительно точки О есть вектор, численное значение которого равно mvd, где d—расстояние точки О до касательной к траектории движения материальной точки (фигура 8); направление вектора момента К устанавливается перпендикуляром к плоскости, содержащей точку О и касательную к траектории; при этом (смотрите Векторное исчисление)

К=[rmv],

где г— радиус-вектор точки М относительно точки О, принятой за начало координат. Проекциями момента К на оси координат будут:

*0; “,—(*§-*1);

Так как

Гrv1

К=2т

[г«]

₂ является секториальной скоростью, то К=2mS,

то есть момент количества движения точки равен удвоенному произведению массы точки на ее секториальную скорость относительно начала координат и по направлению совпадает с направлением секториальной скорости.

М. количества движения системы материальных точек относительно точки О называется геометрич. сумма моментов отдельных материальных точек, составляющих систему. Проекциями момента К в этом случае будут:

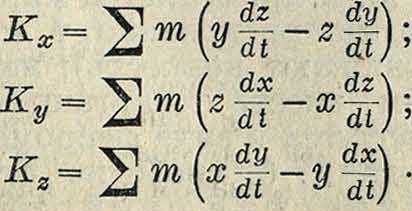
См. Механика теоретическая.

j—&—О

I

I.

Фигура 9.

М. силы Р относительно полюса О (фигура 9) есть вектор Ж, численное значение которого равно P-d, где d — расстояние полюса до данной силы; положение вектора М. устанавливается перпендикуляром к плоскости, содержащей данный вектор Р и полюс О, причем направление вектора М. определяется правилом штопора; в интерпретации векторного исчисления момент представится следующим образом: Ж=[гР],

где г есть радиус-вектор начальной точки данной силы Р относительно точки О.

Обозначив декартовы координаты начала вектора Р через х, у, z, проекции силы Р на координатные оси—через Χ,Υ,Ζ и координаты полюса О через а, b, с будем иметь для составляющих М. следующие выражения:

М_х=Z(y - Ь) - Y(z - с),

Му=Χ{ζ - с) - Ζ{х — а), M_s=Y(x-a)-X(y-b). Аналитическое выражение для момента Ж

будет: ____

М=VMI + Ml + М|.

Если полюс О принять за начало координат, то в предыдущих формулах надо положить а — b=с= 0; тогда

M_x=Zy-Yz,

M_y=Xz-Zx,

M_z=Yx — Ху,

Μ =V(Zy-Yz)² + (Xz-Zx)² + (Ϋχ - Xyf.

Μ. силы относительно точки называется также статич. М. силы, или М. вращения относительно той же точки.

Аналитич. выражение для момента Ж относительно оси I, проходящей через точку О с координатами а, Ь,с и образующей с осями координат углы а, β, у, будет:

М={ Z(y — Ь) — Y(z — с) } cos а + I X(z — с) —

— Z(x — а)}cos β + { Y(x—a)—X(y — Ь)} cosy.

Если О—начало координат, то есть α= Ь=с=0, то

М=(Zy — Yz) cos α + (Χζ — Ζχ) cos β +

+ (Yx — Xy) cos у.

Μ. силы относительно оси I называется также статическим М., или М. вращения относительно этой оси.

Лит.: Жуковский Η. Е., Теоретич. механика, ч. 1, 2, М., 1927; Суслов Г. К., Основы аналитич. механики, т. 1, ч. 1—2, Киев, 1911, т. 1, ч. 3, Киев, 1912; Бобы лев Д., Kvpe аналитич. механики, 2 изд., ч. 1—2, СПБ. 1885—89; Appel Р., ТгаНё de Mftcanique rationntlle, 3 6cl., t. 1—4, P., 1920—24; см. также Механика теоретическая Д. Колянковский.