> Техника, страница 63 > Моторное исчисление

Моторное исчисление

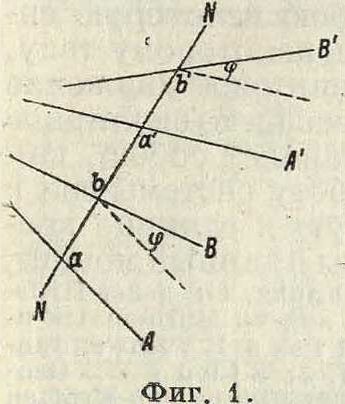
Моторное исчисление, наука о т. н. м 6 тонн о р а х, применяемая в различных отделах теоретич. механики, теоретич. физики и т. д. Мотором вообще называется всякая упорядоченная пара прямых, то есть такая пара прямых, из которых одна условно считается «первой», а другая—«второй». Прямая, перпендикулярная к обеим прямым мотора, называется осью последнего. Если прямые, составляющие данный мотор, не параллельны, то ось имеется только одна; в противном же случае имеется бесчисленное множество осей. Мотором в более узком смысле называется всякая упорядоченная паранепараллельных прямых. Прямые мотора можно либо повернуть на один и тот же угол около оси, либо переместить их параллельно самим себе вдоль оси, либо совершить и то и другое одновременно так, чтобы прямые мотора описали некоторое винтовое движение. Все упорядоченные пары прямых, которые м. б. слиты друг с другом при помощи винтового движения около одной и той же оси, образуют один и тот же мотор. Так, если две пары упорядоченных прямых А, В и А, В имеют одну и ту же ось N (фигура 1), равные взаимные расстояния (аЬ=аЬ) и кроме того А (А, В)=Z (А, Β)=φ, то они представляют один и тот же мотор. Мотор таким образом определяется шестью величинами, а именно: расстоянием аb между прямыми, углом <р между ними и четырьмя параметрами, определяющими положение оси в пространстве. Вектор М_п, проведенный вдоль оси от 1-й прямой ко 2-й, модуль которого, равен расстоянию ab между прямыми i и В, называется длиной мотора. Вектор М, модуль которого равен tg <р, и проведенный вдоль оси мотора так, что его направление вместе с направлением вращения А к В через кратчайшее угловое расстояние последних образует правовинтовуго систему, называется раскрытием мотора.

Пусть имеются два мотора, из которых один определяется прямыми А, В, а другой прямыми А, В,и пусть N и N—соответствующие оси моторов. К прямым N я N можно провести по крайней мере одну общую перпендикулярную прямую С. При помощи соответствующих винтовых движений можно данные два мотора привести в такие положения, что первые их прямые А я А совпа

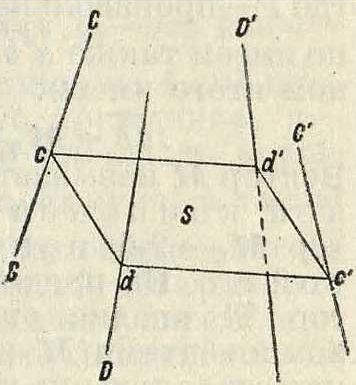
дут с прямой С, прямые же В и В займут при этом положения Ώ и D. Т. о. данные два мотора будут уже представлены парами прямых С, В и С, D, то есть двумя парами прямых, у которых «первые» прямые совпадают. Очевидно, что такое приведение к одной общей прямой можно сделать с любой парой моторов. Проведем произвольную плоскость S, перпендикулярную к С (фигура 2), и, отметив точки пересечения ее с прямыми С, Ώ и D соответственно через с d и d, построим на отрезках cd и cd параллелограм, четвертая вершина которого пусть будете. Нетрудно видеть, что при перемещении плоскости S параллельно самой себе точка с будет перемещаться по некоторой прямой С. Для того чтобы это усмотреть,возьмем прямолинейную прямоугольную систему осей координат, ось Z которой пусть совпадает с прямой С; при этом прямая D будет выражена аналитически ур-иями следующего вида:

х=+ а₂г 1

У=а₃ + а₄г

Аналогично прямая D будет выражена vp-иями:

⁺ (2) у=А, + β& I

При определенных значениях z ур-ия (1) дают координаты точки d, а ур-ия (2)—координаты точки d. Координаты же точки с в соответствии со способом построения этой точки будут:

®с=(^α1 + Al) + (“2 + βζ)Ζ

Ус — («3 + Аз) + (^а 4 + βΐ)^Ζ>

При текущем z ур-ия (3) определяют геометрия. место точки с и представляют собой нек-рую прямую С. Последняя прямая вместе с прямой С образует новый мотор (О, С), называемый суммой двух данных моторов (А, В) и (А, В). Применяя последовательно указанный метод, можно получить сумму какого угодно числа моторов.

Пусть имеется мотор 9К, определяемый прямыми А и В, и точка О вне их. Проведем через О плоскости а и β, перпендикулярные соответственно к прямым А и В и пересекающие прямые В и А в точках b и а (флг. 3). Нетрудно видеть, что отрезок аЬ остается неизменным по величине и направлению, если при одной и той же точке О привести систему 4,Вв винтовое движение; другими сло

вами: вектор аЬ зависит только от точки О и от мотора А, В. В самом деле: если перемещать систему А, В параллельно самой себе поступательно вдоль оси Ν, то очевид но вектор ab не изменит ни своей величины ни своего направления. Чтобы видеть влияние вращения на ab, спроектируем фигура 3 на плоскость, перпендикулярную к Ν, то есть на плоскость, проведенную параллельно прямым А я В. Проекции последних

A и В проходят через точку п, представляющую проекцию оси N. Плоскости а и β будут отмечены следами А_х и В_х (фигура 4), перпендикулярными соответственно к прямым А и В и проходящими через проекцию О точки О. Вектор ab состоит из компоненты аЬ и компоненты, равной расстоянию от А до В и остающейся при вращении неизменной. Неизменной остается также и ком понента аЬ. В самом деле: т. к. 0b₁1 nb и па_х]_0’Ь, той аЬ±0п. С другой стороны, из подобия тр-ков ab_xb и 0пЬ_х получаем:

—7=—г-¹, и так как a b_x=nb_x tg о>,то полу-пО пЬ_х ^{1 1} °

чаем: аЬ— пО tg <р, то есть что длина аЬ зависит от расстояния пО и угла φ между

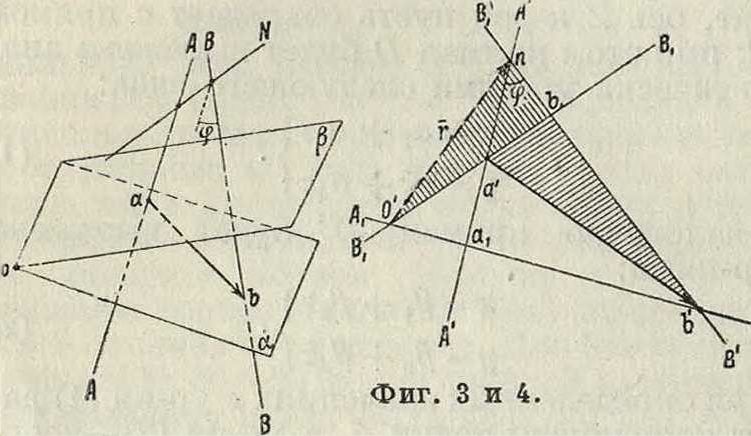
прямыми мотора. Следовательно, если повернуть прямые А, В около точки п на некоторый угол, а прямые А_х, В_х повернуть около О на такой же угол, то аЬ при этом останется неизменным; вместе с тем и ab останется неизменным ври соответствующем вращении прямых А, В и плоскостей а и β.

Вектор М₀=ab называется моментом мотора Ш относительно точки О. Пусть 0п=г_х; тогда очевидно имеем: аЬ=[г“,2ИГ], где М—раскрытие мотора. Если ОР=г, где Р—произвольная точка ochJV.to очевидно имеем также аЬ=[гМ]. В окончательном итоге имеем:

+ [А„В] символически моторное произведение мотогов обозначается след, образом: G== [3(93]. Несмотря на то, что по внешнему виду оба произведения моторов как бы зависят от точки О, они в действительности от этой точки совершенно не зависят.

М. и. находит многочисленные применения в теоретической и прикладной механике, сопротивлении материалов и тому подобное. Так, всякое мгновенное движение тела м. б. представлено при помощи мотора, раскрытие которого определяет направление оси мгновенного винтового движения и величины мгновенной скорости вращения около этой оси, а длина мотора определяет величину мгновенной скорости поступательного движения тела. Данную систему сил F_x, F,.,F_nможно также представить при помощи некоторого мотора, осью которого является центральная ось системы (смотрите Механика теоретическая), а длиной и раскрытием—соответственно равнодействующий вектор F=ZF_Xи главный моментный вектор системы. Если мотор Я представляет собою некоторую систему сил, приложенную к некоторому телу, а мотор 83—мгновенное винтовое движение тела под действием данных сил, то скалярное произведение Я93 представляет собою, как. это нетрудно вывести, работу системы сил к данный момент, отнесенную к единице времени, то есть мощность работы в данный момент.

Лит.: М i s e s R., Motorrechnung, ein neues Ililfs-mitti 1 d. Mechanik, «Ztschr. f. angew. Mathcmatik u. Mechanik», Berlin, 1924, II.2; M i s e s R, Anwendun-gen d. Mot"rriehnung. ibid., H. 3; Study !£. Geo-metrie d. Dynarm n, Die Zusamniens( tzung von Kriiften u. verwandte Gcginstande d. Geometric:, Lpz., 1 903; В i e 7. e n о C., Geonn trie d Iirafte u. Massen, Handb. d. Physik, hrsg. v. H. Geiger u. K. Scbeel, B. 5, p. 247, B., 1927. M. Серебренников.