> Техника, страница 64 > Напряженное состояние

Напряженное состояние

Напряженное состояние, такое состояние тела, при к-ром деформация его под действием уравновешенных внешних сил прекратилась и все частицы тела пришли в равновесие. Если в теле, находящемся в таком состоянии, провести мысленно разрез, то обе части его должны находиться в равновесии, что возможно только при условии, что по поверхности разреза будут действовать какие-то внутренние силы, равнодействующая которых будет уравновешивать действие внешних сил, приложенных к каждой части тела. Эти внутренние силы называют внутренними силами упругости и соответственно Н. с. тела часто—с о с т о я-н и е м упругого равновесия. В общем случае внутренние силы распределяются по поверхности сечения конечных размеров неравномерно, но если мы выделим вокруг точки А на поверхности сечения v очень малую площадку Δω, то в пределах такой площадки можно допустить, что силы распределены равномерно. Деля на площадь этой площадки передаваемую через нее часть SR общей равнодействующей внутренних сил R, получим среднее значение напряже-ния для площадки Δω. Уменьшая эту площадку до нуля и притом так, чтобы контуры площадки заключат)! в себе точку h, мы для

ΔΗ

в пределе получим напряжение в точке А:

α= Пт

Δω—Ю

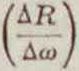
dR da) *

(i)

к-рое т. о. для данного сечения v при неравномерном распределении напряжений определяет интенсивность внутренних сил упругости в точке А.

Величина равнодействующей R определяется из условия равновесия ее с внешними силами, приложенными к рассматриваемой части тела. За направление напряжения а принимается направление равнодействующей, относящейся к данной точке; т. к. направление это вообще неизвестно, то при изучении Н. с. изучают слагающие напряжения: и— нормальное к поверхности площадки и I—касательное к ней. Нормальные напряжения вызывают растяжение или сжатие материала в точке, а касательные—сдвиг или срезывание. В общем случае напряжение в точке характеризуется слагающими по трем осям координат, для чего вводятся следующие условные обозначения. Напряжение, относящееся к площадке, перпендикулярной к оси х-ов и параллельное самой оси, обозначается двумя одинаковыми индексами »!_я; очевидно, что это напряжение, нормальное к площадке. Напряжения, относящиеся к той же площадке, но параллельные другим осям, обозначаются также двумя значками, причем первый определяет площадку, к которой относится напряжение, а второй — направление напряжения: t_xy, t_xzи т. в Эти напряжения очевидно являются касательными к площадке, нормальной к оси х-ов (фигура 1). При определении направления этих напряжений принимают нормальные напряжения растягивающими, то есть вы

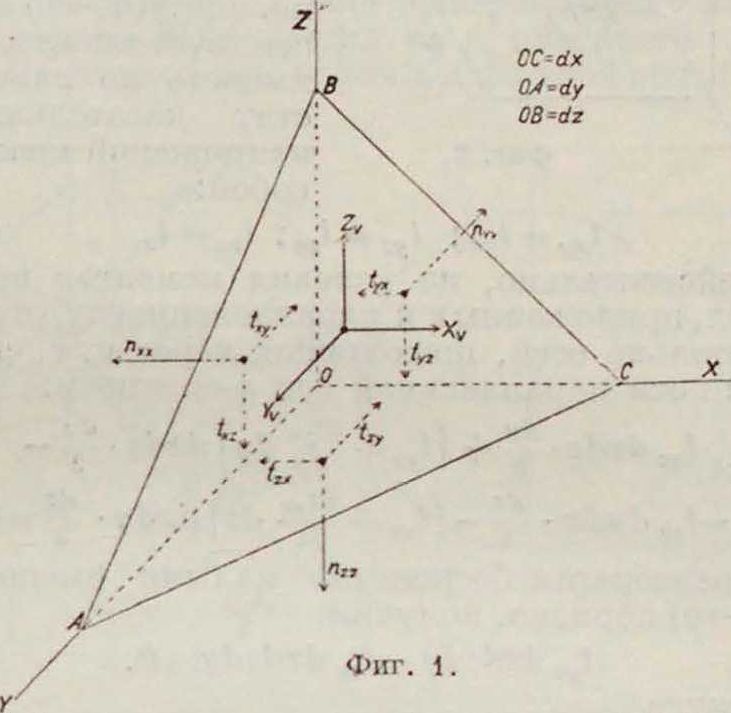
ходящими из сечения; направления же касательных напряжений принимают по соображению с направлением нормального напряжения; если последнее направлено в сторону положительного направления оси, то направление касательных напряжений принимается по положительному направлению двух других осей; если же направление нормального напряжения принято по отрицательному направлению оси, то и направление касательных напряжений принимается по отрицательным направлениям соответствующих осей (фигура I).

Через любую точку тела можно провести бесчисленное множество различно направленных площадок, но напряжение по любой из этих площадок м. б. найдено, если известны напряжения по трем взаимно перпендикулярным площадкам, проходящим через ту же точку, что вытекает из условия равновесия тетраэдра ОАВС, к-рый можно представить себе вырезанным из тела в рассматриваемой точке О плоскостью v (АВС) и тремя плоскостями по направлению координатных осей, на которых плоскость v отсекает бесконечно малые грани dx, dy и Лг. стремящиеся к нулю, что позволяет считать напряжения во всех четырех плоскостях тетраэдра отнесенными к точке О тела. Если обозначить площадь грани АВС через ω„, то пло-

щади остальных граней тетраэдра определятся величинами со_г cos (ж, V), ω„ cos (у, ν), ω₀ cos (ζ, ν).

Из условия проекции на каждую из осей после сокращения на со, получаем: X₁,=n_Kccos(a;,i;)-btj_№cos(j/,«t+i«cosC2,v) Y_r=n_!lycos(y,v)+t_X!lcos (x,v)+t_ZyCos(z,v) >.(?)

=«« cos (2,v)+ty, cos (iM>)+i*»cos(a:,y)) Таким образом слагающие напряжения по плоскости у определяются девятью слагающими напряжений по координатным плоскостям тетраэдра. Из рассмотрения прямоу-гольн. параллелепипеда (фигура 2), который вырезан из тела у той же точки, следует, что существует такая взаимность по равенству касательных ν Фпг. г. напряжений между собой:

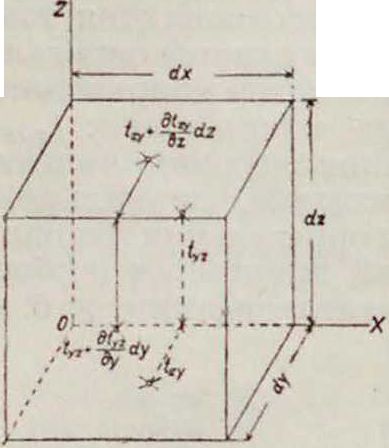
t ху Iух j (уг ⁼ ^XZ-

Действительно, из условия моментов всех сил, приложенных к параллелепипеду, относительно осей, проходящих через ц. т. его, для оси параллельной оси ж-ов имеем:

t_vz dxdz · ^dw 4- (i_y34- ^dt6^v* dyj dxdz ^dv -

dydx ^d* - (l„ + ** dz) dxdy · ^dz - 0.

Пренебрегая бесконечно малыми высшего (4-го) порядка, получим:

i уз dxdzdy — 1_tv dxdzdy=О,

откуда

V

Аналогично может быть доказано, что

t ху ^уХ И t ZX ^ Ιχζ

Эта взаимность между касательными напряжениями приводит к тому, что для определения слагающих напряжений в любой плоскости надо знать шесть элементов составляющих напряжений в трех координатных плоскостях.

Проекция напряжения в плоскости у на нормаль к этой плоскости определится как сумма проекций составляющих п_т=Х„ cos (у, х) + Y_v cos (v, у) +

+ Z_rcos(v, z), (4)

или, подставив значение X_r, Y_v и Ζ, и сделав приведение, получим:

“ ^пхх COS² (г. X) + Пу„COS* (У, ?/) +

-f cos² (у, г) 4- 2l_xy cos ро, ж) cos (у, у) 4-4-2t_yz cos (у, у) cos (у, г) 4-4- 21_хг cos (у, х) cos (у, г). (5)

Если площадка у поворачивается вокруг точки О и если в соответствии с ее поворотом откладывать по нормали к площадке отрезки (?= 1: Vn_m, то координаты концов этого отрезка будут:

х=о cos (у, ж); у=ρ cos (у, у);

2=о cos (у, г). (6)

Подставив значения косинусов в выражение (5) напряжения п_т, получим:

«я ж² 4- п,_/у ?/²4- У _гз г²4-4- 2 t_xy ху+ 21_уг уг + 2t_yx xz=1, (7)

то есть уравнение второго порядка. Изменяя направление координатных осей, можно выбрать такое направление их, что коэф-ты при членах с произведением координат будут равны 0. Для таких осей слагающие касательные напряжения будут равны нулю, и останутся только нормальные напряжения. Плоскости, к которым относятся эти оси, носят названия главных плоскостей с е ч е-н и я, а относящиеся к ним нормальные напряжения—г лавныминормальными напряжениями п_п, и₂₂ и п₃₃. Величины этих нормальных напряжений определяются корнями кубического ур-ия:

-п³ + (п_хх4- п,п_хх — if.

+ п, + n,_z)n*-{n_xxv

4- 2t_xu t_x

f ²

. ___ _aa

"xy z; lyi ~ ⁿxx tyz ~ ⁿyy tX3 ~ ⁿsz I flx) ⁼ 0. (8)

Оно получается из ур-ия (2) подстановкой в него вместо величин Χ_τ, Υ„, Ζ_ν значений их, которые выражены через главные напряжения п:

уу

<**) η 4- (п_хх Пуу и,

s +

4-

Х_Т=и cos (у,ж); y„=ncos (у,?/); Z„=ncos (ν,ζ) и исключением из полученных этим путем трех ур-ий косинусов углов, связанных между собой условием

cos² (у, ж) 4-cos² (у, у) 4- cos² (у, 2)=1. (9) Из выражений (6) и (7) непосредственно видно, что сумма нормальных напряжений независимо от направления координатных осей есть величина постоянная:

п_тх + п_уу 4- п_я=щ 4- «j 4- «з=Const. Если отложить отрезок п„ по направлению нормали к плоскости у от начала координат главных плоскостей, то координаты вершины отрезка будут:

х=ⁿvx=% cos (у, ж); у=n_ry *= п₂ cos (у, у); ζ=п_тг= w₃cos (у, г);

но так как косинусы углов связаны условием (9), то след, при вращении площадки полное нормальное напряжение к ней при различных положениях ее определяется отрезками, вершины которых очерчивают поверхность эллипсоида, называемого эллипсоидом напряжений. Когда одно из главных напряжений обращается в нуль, то эллипсоид обращается в эллипс, и напряжения для всех положений площадки будут лежать в одной плоскости; такое состояние тела называется плоски м напряженным с о-стоянием (плоская задача). Если два главных напряжения обращаются в нуль, то получится линейное напряженное состояние. Большинство технич. задач приводится к плоскостному и линейному II. с., которые представляются более простыми для решения, чем пространственные, и рассматриваются в курсах сопротивления материалов. Вопросы о пространственном напряженном состоянии рассматриваются в курсах теории упругости.

При плоскостном H. с. тетраэдр, показанный на фигуре 1,приводитсяк треугольн.призме ^ (фигура 3) с бесконеч но малыми сторонами dx и dy и длиной по оси г, равной единице. В этом случае напряжения ««=(«= (»»= 0. Если же обозначить угол наклона площадки V к оси ar-ов через а, то напряжение п_т, нормальное к этой площадке, определится следующим выражением :

n_v=n_m sin a -f n_ry cos a =

= n_x sin² a -f n_y cos² a + t_xy sin 2a, (10)

и напряжение касательное к ней, определится выражением:

^v⁼ⁿvx cos а — n_vy sin α =»

“ 2 (и“ — п_у) sin 2α + t_xy cos 2α. (11)

Наибольшие значения нормального и касательного напряжений определяются из условий:

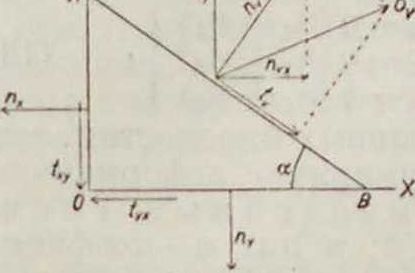
Фигура з.

dn_r

= 0 и

dir

da

= 0.

По первому из этих условий будем иметь: 2n₂.cosa₁sina₁—2n_vsina₁cosai + 2<_I1,cos2a₁=0, откуда следует, что площадка с наибольшим нормальным напряжением наклонена к оси х-ов под углом

tg 2a,

2‘τν

(п_х-п у)

(12)

Выразив величины cos² a и sin² а в функции угла 2a_lt из (10) получим:

= 2 + ⁿji) - 2 (“«-%) cos2a,+/sin 2a,. (13)

Подставив в него значение cos 2a_t и sin 2a, из (12,), получим выражения главных напряжений, максимального—п₁ и минимально-го—п_г в таком виде:

2 («.г "Ь Ну) («* «у)" “Ь 4£χ^,

«2=2 (Пх + Пу)-(п_х-п_у)· + 4Ц_у; (14)

оба напряжения в, и и₂ взаимно перпендикулярны. Из сложения их вытекает, что «i + «г=и“ + «у=Const.

Из выражения (11) касательного напряжения 1, видно, что для главных плоскостей течения ί=0. Наибольшее значение касательного Напряжения определяется из ус-

dt_r л ловил.=0, то есть пи ⁷

(15)

(п_х — «у) COS 2a„ — 2t_xy sin 2a ₂=0, которое удовлетворяется при условии о _ _ (Βχ — Пу) 1

² Щу из чего следует, что площади сечения с наибольшим и наименьшим значениями касательного напряжения направлены под углом °2=^αι + 45° и а₂=а, -+- 135° к координатным плоскостям или под углом 45° и 135° к главным плоскостям сечения. Величина наибольшего (_х и наименьшего <₂ касательного напря жения определится после подстановки значения tg 2a₂ в выражение (11):

= * ]/(«* - «у)² + Щ_у h=- i_a. (1G)

Величины напряжений по различным плоскостям сечений, проходящих через точку, м. б. определены графически при помощи круга Мора. На фигуре 4 построен круг Мора на главных напряжениях п₁ и п₂ (в данном частном случае значения и гг₂ взяты разных знаков, а именно: п_х—положительное, а и₂ — отрицательное). Разность этих напряжений [п_х — «J образует диаметр круга. Если взять какую-либо точку С круга и опустить из нее перпендикуляр на диаметр, то из чертежа нетрудно видеть, что

OD= 2 («i 4-н₂) ’ («i—n₂)cos 2α= Пу,

CD= I (n,—n₂) sin 2a=t_XIJ,

T. e. отрезок OD по диаметру круга, как абсцисса точки С, определяет величину нормального напряжения п_у в плоскости С1, наклоненной под углом a к главной оси (13),

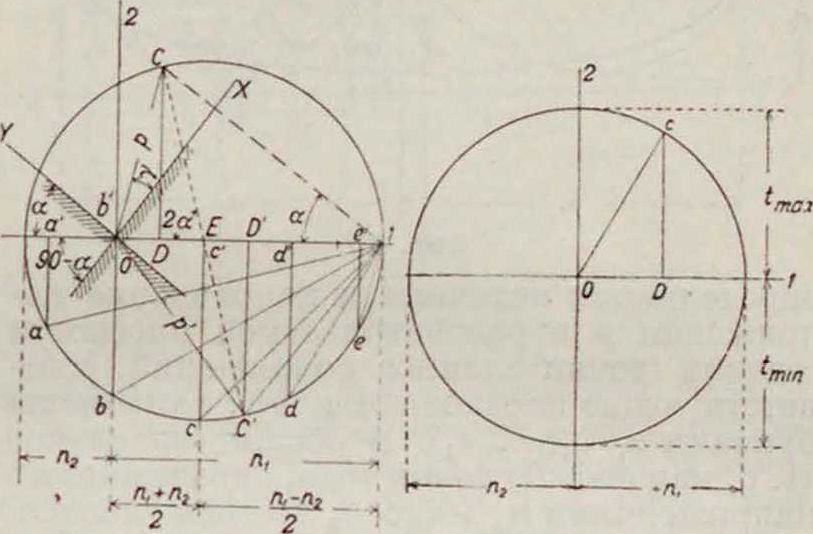
Фигура 4. Фигура 5.

и отрезок GD определяет величину касательного напряжения t,_JX в той же плоскости (11). Напряжения п_х и t_xy в плоскости перпендикулярной определяются отрезками OD и DC. Из чертежа видно, что истинное положение и величина напряжений в этих площадках определяются отрезками р=Κη|+ /|χ и р=Vnl + ily.

На фигуре 5 показан круг Мора для случая чистого сдвига, когда

<max=l [Wi-(-«2)]=«l· (¹⁷)

Па фигура G сделано построение эллипса напряжений на полуосях 01=п, и 02=«₂ и кривых (роза), характеризующих развитие нормальных и касательных напряжений по направлению любых плоскостей. Для построения этих кривых проводим на круге

Мора ряд плоскостей сечений 1—a, 1—b.

1—е и такие же плоскости проводим через центр эллипса. Откладывая по направлению перпендикуляра к каждой из этих плоскостей отрезки Оа, Ob, ., Or, получаем по ним кривые 2 а Ь Осd е1, характеризующие изменение величин наибольших нормальных напряжений. Откладывая в самих плоскостях отрезки Оа", ОЬ", ., Ое", получим кривую Оа" b" с" d" е" О (на фигуре 6—пунктирная), определяющую величины касательных напряжений в различ-

ных плоскостях. Указанным построением такие кривые могут быть получены для каждой четверти. Проведя например плоскость иод углом а к главной оси 1—2, получим в пересечении ее с пунктирной кривой точку С_1у определяющую величину касательного напрялсения UC₁=t_yx, проведя к той же плоскости перпендикуляр, получим в пересечении его со сплошной кривой точку D, определяющую величину нормального напрялсения OD =п_у. Отрезком ОС=р, вершина которого лежит на эллипсе напряжений,

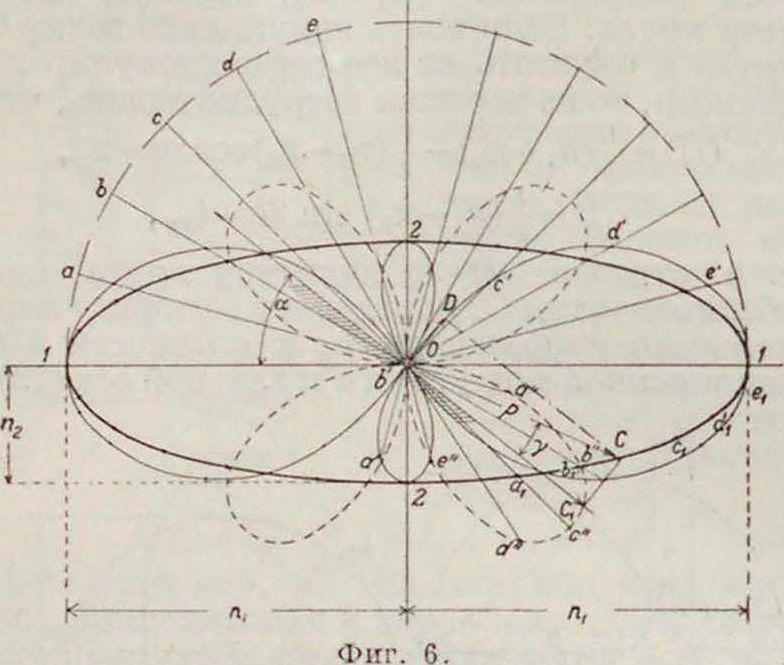
определяются величина и направление напрялсения р в рассматриваемой плоскости сечения (точки эллипса напряжений, соответствующие плоскостям а, b.е отмечены буквами Oj, b_u. е_г). 15 общем же случае И. с. какой-либо точки тела, определяемого напряжениями п₁ > п₂ > п₃ по трем главным плоскостям, зависимость между напряжениями в любых плоскостях определяется тремя Кругами (фиг .7): для плоскости сечения, параллельной плоскости 1 — 2,—кругом АВ, для плоскости сечения, параллельной плоскости 2—3,—кругом АС и для пло

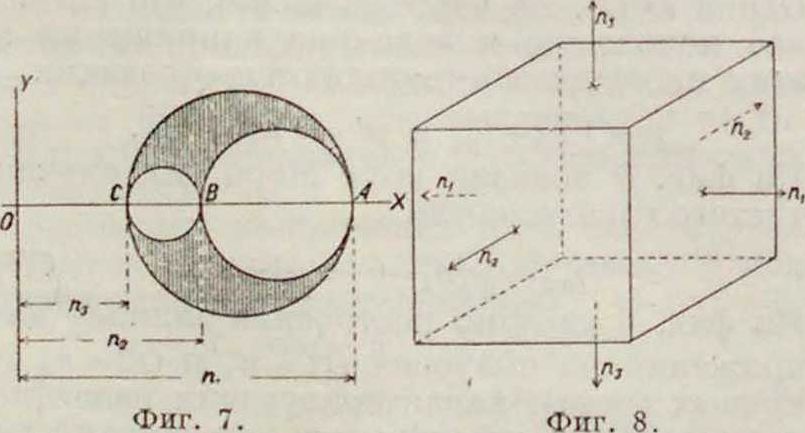
скости, параллельной 2 — 3, — кругом ПС. Для плоскостей, пересекающих все три координатных оси, напряжения в них изображаются координатами точек, лежащих в заштрихованной площади.

Выведенные выше величины наибольших суммарных напряжений выражены в функции слагающих напряжений, определяемых по равнодействующими моментам, вызываемым в сечении действием внешних сил. Но по закону Гука всякое напряжение является линейной ф-ией от деформации (смотрите). В телах изотропных, имеющих одинаковые упругие свойства во всех направлениях, эта ли нейная зависимость упрощается (смотрите Деформация, ф-лы 9 и 10), что позволяет величины наибольших напряжений по направлению главных осей, обозначенные условно через [и], выразить следующими ф-лами (фигура 8): [и,]=Ее_х=η, - η («₂ + п₃) I [«,]=Ее_г=п_а- тонн) (гц + п₃) (18)

|>₃]=Ее₃=η₃ - η (щ + п_г) )

Эти напряжения в главных плоскостях, выраженные через суммарную деформацию, носят название приведенных главных н а п р я ж е н и й; в них η—коэфици-ент Пуассона. При плоскостном действии сил н₃=0, потому приведенные напряжения определяются выражениями:

Od=щ~ η п_г и [ίΐ₃]=«₂-ί?η₁, (19)

к-рые после подстановки в них величин п₁ и и₂ по ф-лам (14) приводятся к виду:

[«d=έ (1 - V) (п_х+ п_у) +

+ έ(1.+ P)V(n_x-n_yf+ (20)

[и“] - (Μχ+ Пу)~

- i (1 + n)V(n_x- n_vf+ ithj.

Величины касательных напряжений определяются но углам сдвига е_ху, с_у;, е,_х (ста.,Деформация, формула 9):

^ху~ (^J&xy > ^yz~ (*Cy_Z. tχ~ ⁼ Gϋχ., (21)

где G—модуль упругости при сдвиге.

Входящие в выражения наибольших нормальных и касательных напряжений величины напряжений и_хх, п_уу, n_zz, i_xy, t„, t_yzв координатных плоскостях определяются из условий равновесия тела при рассечении его по направлениям этих плоскостей. Для их определения сложное действие внешних сил на тело расчленяют на простые: действие продольной силы (растяжение и сжатие), действие поперечной силы (сдвиг и срезывание), поперечный изгиб и кручение (смотрите Изгиб, Кручение). При действии продольной силы N, направленной вдоль оси бруса и приложенной в центре тяжести сечения его. напряжения в сечении, нормальном к оси бруса, будут t_xy= 0, п_х=±¹^=п₁,

из чего следует, что нормальное напряжение в этом сечении является главным и и_г=0. В плоскостях, наклоненных под любым углом а к оси, напряжения будут определяться выражениями (формулы 10 и 11):

п=ftjCOS² α= ^Λ COS² а; ί_α= J ^Λ sin 2α.

Наибольшее касательное напряжение имеет место в сечениях, наклоненных под углом

α= 45° к оси бруса, когда t=*^wi · При дей-ствии поперечной силы Q, направленной перпендикулярно к оси бруса, деформация бруса всегда сопровождается не только сдвигом сечения одно относительно другого, но и изгибом. В отдельных случаях практики (срезывание в заклепках, во врубках и тому подобное.) принимают, что касательное напряжение в сечении, нормальном оси, распределяется равномерно по сечению и определяется величиной <“,=^Q, причем в этом сечении п_х— п_у= 0, что соответствует случаю чистого сдвига (ф-ла 17). Наибольшие и наименьшие нормальные напряжения имеют место в пло-

•скостях, наклонных под углами ±45° коси; величина их (ф-ла 14): riy= — n_t= <=

При кручении, возникающем под влиянием момента М_:, плоскость которого нормальна к оси бруса, в сечениях бруса, нормальных к оси, развиваются только касательные напряжении, которые для брусьев круглого сечения определяются величинами (смотрите Кручение):

. -W. л

t_xy — г, n_x — Пу — О,

‘ е что соответствует случаю чистого сдвига (ф-ла 17) (/_е — полярный момент инерции площади поперечного сечения). Наибольшие нормальные напряжения имеют величину <ф-ла 14):

+ tx,j= ψ-r, п_а=-η,

‘_e

и относятся к сечению, наклоненному под углом 45° it оси бруса (ф-ла 15).

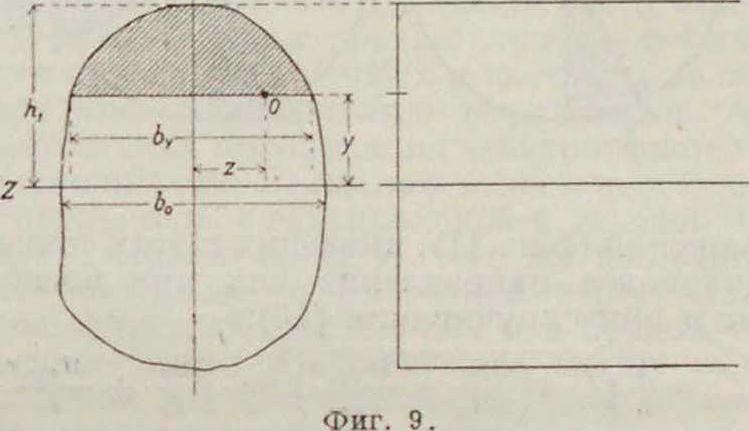
Напряжение при чистом изгибе, вызываемое действием сил, лежащих в одной из плоскостей, совпадающих с направлением главных осей поперечного сечения бруса (фигура 9), определяется выражением (смотрите Изгиб):

м. м_{и Λ}

«*=у- у ИЛИ У1_Х=-*ζ и п_у=О,

в которых I, и 1у—моменты инерции сечения, а у и г—координаты рассматриваемой точки. •Очевидно, что наибольшие напряжения имеют место в крайних точках сечения м. м„

^{или П}*=Ку’

в которых M, и V_y—momchtiiI сопротивления сечения. В большинстве случаев практики изгиб сопровождается действием поперечной силы, и тогда напряжения в отдельных точках сечения определяются величинами:

Мл у _{?г =}0 I=9 ^sh -l

I_t J’ "ν ^υ> I. by

в которых S_h__y—статич. момент части сечения от уровня рассматриваемой точки О до контура сечения (фигура 9), Ь_у—ширина сечения на уровне точки. Одновременное действие изгибающего момента и поперечной силы является одним из наиболее распространенных случаев комбинированного действия сил. Величина наибольших нормальных и касательных напряжений, определяемых по формулам (14) и (16), будет меняться в зависимости от положения точки в сечении. Для точек, наиболее удаленных от оси сечения, напряжения будут:

ⁿi= y; w»=0; 1=0;

для этих точек сечение, нормальное к оси бруса, является главным сечением; и т. к. для него «₂=0, то эллипс напряжений в этих точках обращается в прямую линию (фигура 10, ί— 1 в крайней верхней точке сечения и 2—2 в нижней). Для точек, расположенных на оси бруса,

«1 ” «2=0, _тах=- Ц,-„=;

для этих точек в сечении, нормальном к оси, имеет место чистый сдвиг; эллипс напряжения в этих точках превращается в круг.

Для всех остальных точек сечения главные напряжения определяются величинами (14):

1,2

и наибольшие касательные величиной (10):

.

причем нормальное напряжение будет направлено под углом dj (13):

„О_а ^QSh-yl -2QS;_t-y

° ~ ¹ by - Μ V M by у

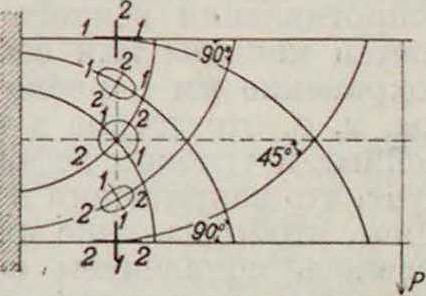
На фигуре 10 показано приближенное очертание и направление осей эллипса напряжений в этих точках.

При сложном действии внешних сил и моментов, вызывающих каждое в отдельности нормальные напряжения, величина сум-

Y

марнОго нормального напряжения определяется на основании закона о независимости действия сил простым алгебранч. сложением по величине и знаку. Так например, при внецентренном действии продольной силы, приложенной к точке с координатами а и Ь, что сопровождается действием в сечении бруса продольной силы N и моментов М_х —=Να и M_y=Nb, нормальное напряжение для любой точки сечения с координатами х и у определяется выражением:

N М_х, Му N (, аи Ьх

№= +-г⁵2/+,а;= 11+, + —1.(22)

где Q_x и Qy—соответственные радиусы инерции, из чего следует что в общем случае действия силы и мо- ’ ментов нормальное напряжение распространяется по сечению по закону плоскости.

Прнодновременном действии на брус круглого сечения изгибающего и закручивающего моментов, что сопровождается развитием в сечениях бруса нормальных к оси напряжений

Фпг. ю. п,=

·%, ₌9^sJtt t

величины наибольшего и наименьшего нормальных напряжений будут иметь место в точках, наиболее удаленных от нейтрального слоя (фигура 11), и определяются из следующих выражений (14):

Наибольшее касательное напряжение в той же точке будет (16)

Наибольшее же касательное напряжение в крайних точках нейтрального слоя определяется из суммирования касательных на

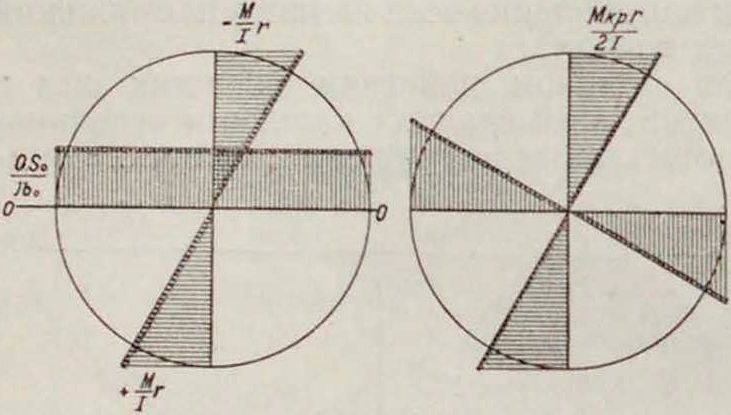
Фцг. и.

Мц,г

21

пряжений (фигура 11), имеющих в этих точках одинаковое направление как при изгибе, так и при скручивании (16):

1 _ЛГ ₄/УЗо.

• 2 V ⁴U П_г ^± 1_г )

QSg Mfcp.r 2rl_z * ϊ_ζ

В качестве условия прочности при рассмотрении комбинированного действия кручения и изгиба чаще пользуются ф-лой приведенных главных напряжений (20), по которой наибольшее нормальное приведенное напряжение определяется величиной:

м_в + ¹⁺2^чУ М1 + MQ;

при η=0,3 это выражение принимает вид:

[»Ч] - ^ (θ,35Μ, + 0,65 УЩ + Щр.у выражение, известное под названием ф-лы Сен-Венана.

Вопрос изучения Н. с. тела имеет своей целью определение необходимых размеров тела по условиям прочного сопротивления материала самого тела. Условием прочного сопротивления всякого тела, входящего в состав машины или сооружения, является сохранение им первоначальной своей формы, то есть отсутствие в теле остаточных линейных и угловых деформаций; отсюда следует, что напряжения в частях тела должен быть таковы, чтобы наличие их в теле не сопровождалось появлением остаточных деформаций. В связи с этим выбор размеров каждого тела или каждой детали машины ограничивается величиной допускаемого н а-пряже Н и я. Величина допускаемого нормального напряжения п₀ выбирается как некоторая доля от временного сопротивления R материала или его предела упругости,

т. e. я₀=* R, где к—коэфициент запаса прочности, величина которого изменяется сообразно с однородностью упругих свойств материала и работой машины или сооружения. Самый расчет прочности делается но одной из формул напряжений в соответствии с тремя теориями прочности (смотрите Прочность). Если расчет делается по первой теории прочности, то есть по величине наибольшего напряжения, что справедливо для случая линейного действия сил на тело, то используется формула (14) главных напряжений, и напряжение п_г должен быть $ п₀. Когда расчет прочности делается из условия, что линейная деформация не должна превосходить известного предела, то в случае пространственного действия сил используется формула (18), по которой

[%]=(и, + П_ъ) .< П₀.

При плоскостном действии сил определение напряжения делается по ф-лам (16) или (20), по к-рым

[«J=«1 - >/П₂ < П₀.

Если расчет производится по третьей теории прочности из условия, что в теле не должен быть остаточных угловых деформаций, то допускаемое напряжение на сдвиг t₀ определяется из выражения касательного напряжения через главные (ф-ла 11 при α= 45°)

2<₀= iii —n_a=sw₀.

Расчетное напряжение определяется по формуле (16) из условия t_max ^ 0,5 ?г₀.

Изучение И. с. при сложном действии сил не всегда разрешимо при существующем развитии теории упругости и сопротивления материалов. Существенную помощь в этом изучении при плоскостном действии сил оказывает оптический метод (смотрите Деформация), основанный на том, что запаздыванием лучей, пропускаемых через напряженную пластинку, определяется разность главных напряжений, то есть величина наибольших касательных напряжений 2t-n₁—n_i. При пропуске через пластинку белого света последний в силу явления хроматин, поляризации разлагается на ряд цветов (кольца Ньютона), которые оттеняют распределение напряжений по пластинке; так, одноцветность показывает, что разность (n_t—n_t) одна и та же; это дает возможность проследить развитие в теле т.н. траекторий напряжений (смотрите Деформация, вкл. лист). Места, остающиеся на пластинке обесцвеченными, показывают, что в них отсутствуют сдвиги, т. e. t= 0, а это соответствует равенству главных напряжений. При наличии эталона, подвергающегося одновременно растяжению определенными силами и в соответствии с этим изменяющего свою окраску, представляется возможным определить разность напряжений (п₁ — п“) по хроматич масштабу (смотрите Деформация). Наконец, измеряя при помощи точнейших приборов (в сотых долях μ) изменение А<5 толщины пластинки в изучаемой точке, можно определить сумму главных напряжений из условия:

где Е—модуль упругости материала пластинки, а η—коэфициент Пуассона для нее. Таким образом при помощи оптического метода выявляются: направление главных напряжений и величины (и,—я₂) и (n_l+w_i). чем они вполне определяются.

Лит.: М и тине к и ή II., Строительная механика, CIII3. 1914; Тимошенко С., Теория упругости, ч. 1, СПИ, 1914; Зайцев А., Оптич. метод изучения напряжений, Л., 1927; Love А. A Treatise on tile Mathematical Theory of Elasticity, Cambridge, 1928; F 0 p p 1 A., Vorlesungen uber technisclb; Mechanik, 4 Aufh, И. Ь, B.—Lpz, 1922; CokcrE., FOppl A. u FOppl L., Drang u. Zwang, В. 1. 2 Auf 1., Mch.—B., 1924, B. 2, Mch,—B., 1920: Coker E., The Determination by l’hoto-Elastie Methods of the Distribution of Stress, «Trans, of the Inst, of Naval Archit.-. L. 1911. И. Прокофьев.