> Техника, страница 64 > Начертательная геометрия

Начертательная геометрия

Начертательная геометрия, наука о методах, изображения на плоскости пространственных фигур. Методы эти должны дать такое изображение фигуры, при к-ром по чертежу можно было бы судить об истиц-

нон форме и размерах ее и которое было бы наиболее наглядным, то есть при известной привычке производило бы на нас впечатление пространственного, а не плоского образа. Для целей геодезии, технич. черчения и картографии б. ч. вполне достаточно удовлетворить первому требованию. Для архитектора и художника второе требование является более существенным. Соответственно атому в первом случае чаще употребляются теоретически более простые, но не всегда дающие наглядный рисунок методы—о рто-тональной проекции на одну или несколько плоскостей, во втором случае— метод наиболее близкий к процессу человеч. зрения — централ ь н о е проект и р о-нанне. пли перспектива. Простейшие изображаемые нами предметы ограничены плоскими гранями; эти грани ограничены прямолинейными контурами; важнейшие, бросающиеся в глаза, точки—вершины этих контуров, то есть точки пересечения нескольких прямых линий.

Естественно поставить требование, чтобы при изображении таких фигур прямые линии изображались прямыми, а вершины переходили в вершины. Различные грани фигуры мы изображаем на одной и той же плоскости—плоскости чертежа, то есть производим отображение одной лежащей в трехмерном пространстве плоскости на другую. Наиболее р

ФИГ. I.

•общее преобразование одной плоскости в другую, при котором прямые переходят в прямые, а вершины в вершины, есть проективное преобразование, или к о л л и-н е а ц и я. двух плоскостей. Все употребляемые в И. г. преобразования суть частные случаи наиболее общих проективных преобразований, учение о которых составляет содержание пр оектнвной геометрии (смотрите Геометрия). Эти же методы годятся и при изображении предметов, не имеющих плоских граней и прямолинейных контуров, например кривых линий и поверхностей; но при этом следует помнить, что только прямолинейные контуры сохраняют свою прямолинейную форму; форма криволинейного контура, вообще говоря, меняется.

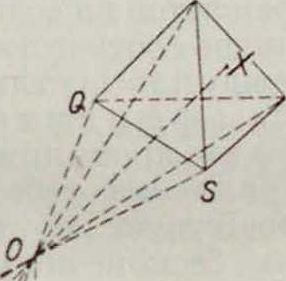
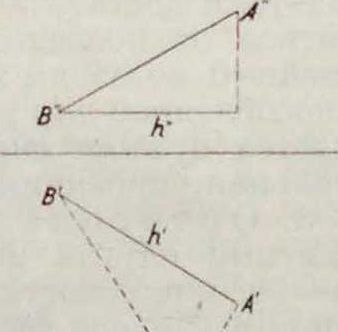
1. Центральная проекция, или перспектив а. Преобразование перспективы есть проектирование фигуры из некоторой точки—центра перспективы—с вязкой лучей (то есть совокупностью лучей, проходящих в пространстве через центр). Перспективным образом точки×предмета является на плоскости Т (фигура 1) точка А" пересечения луча ОХ с плоскостью Т. Перспектива есть именно то преобразование, к-рое производит наш

глаз при наблюдении предмета: лучи зрения, проходя через глаз (центр перспективы), переводят все точки предмета в плоскость нашего зрения. Поэтому перспективные чертежи—наиболее наглядные, выпуклые, если мы правильно на них смотрим, то есть совместим глаз с центром О. Опуская из О перпендикуляр на плоскость Т, мы по его основанию Н н длине d узнаем расположение

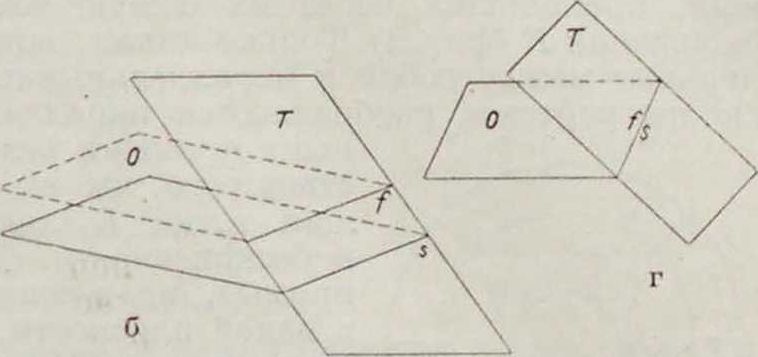
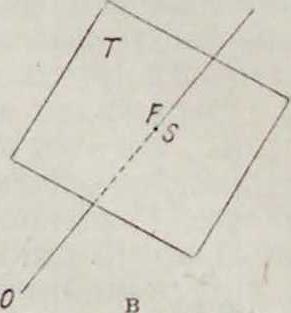
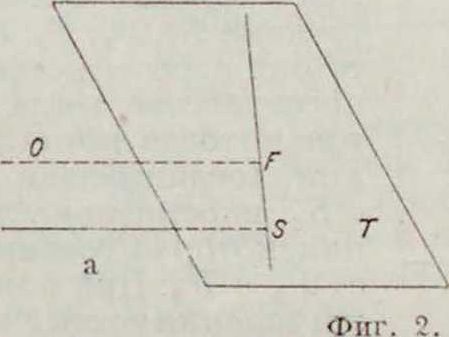
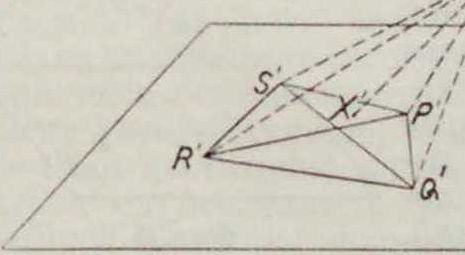
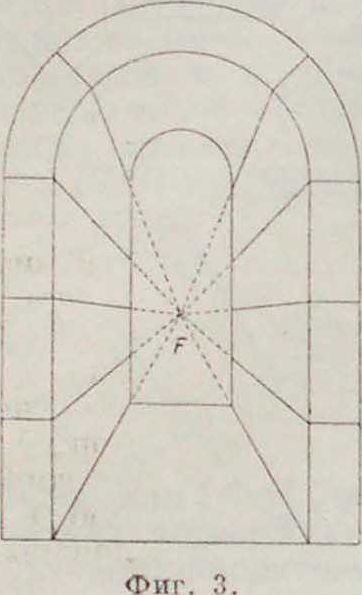
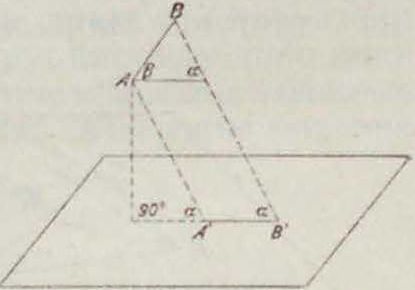
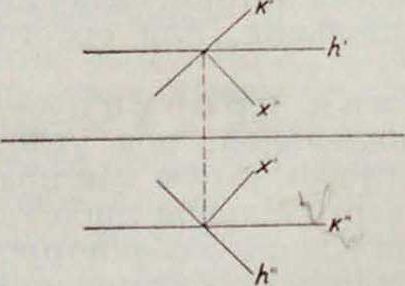
центра. Прямые при перспективе переходят в прямые, вершины—в вершины. Перспектива есть следовательно преобразование проективное. Плоскость, вообще говоря, ото¹ бражается во всю плоскость чертежа. Проективное соответствие, устанавливаемое при этом между плоскостями, называется пер-спективитетом ихарактеризуетсятем. что линия пересечения плоскостей (ось перспективы) сама себе соответствует, так как для точек этой прямой Х=Х. Задача Н. г. состоит не только в умении отобразить данную пространственную фигуру на плоскости, но и обратно—в том, чтобы по готовому чертежу определить положение в пространстве изображенных на нем линий и плоскостей. Ищем поэтому на чертеже те точки прямых и плоскостей, задание которых однозначно определяет их положение в пространстве. Известно, что любая пара точек однозначно определяет прямую, тройка точек или пара параллельных или пересекающихся прямых однозначно определяют плоскость. Для простоты выбираем не произвольные. а вполне определенные точки и линии (фигура 2а и 26): 1) след прямой (плоскости), то есть точку S (линия s) ее пересечения с плоскостью чертежа, и 2) т о ч к у F (линия /) схождения, определяющей > направление (положение) прямой (плоскости) в пространстве и находящуюся на пересечении прямой (плоскости), параллельной данной прямой (плоскости) и проходящей через центр О. Говорят, что точка F (линия /) схождения есть перспективный образ бесконечно удаленной точки (прямой) нашей прямой (плоскости). Линии п s параллельны между собой. Для прямых (плоскостей), проходящих через центр О, точки F и S (линии f п s) совпадают (фигура 2в и 2г). Для прямых и плоскостей, параллельных плоскости чертежа, точки F и S и линии и s лежат в бесконечности. Во всех случаях кроме последнего точки F и S однозначно определяют прямую, линии и s—плоскость. Точки пересечения двух прямых переходят в точки пересечения на чертеже. Параллельные прямые переходят не в параллельные на чертеже, а в пересекающиеся—пучок прямых, проходящих через их общую точку схождения F (фигура 3). Только линии, параллельные между собой и параллельные плоскости чертежа, изображаются параллельными прямыми вследствие того, что их общая точка F лежит в бесконечности. Две прямые, не лежащие в одной плоскости, не пересекаются. На чертеже они пересекутся. Если прямые заданы точками S₁,F₁; S_a, F₂. то они пересекаются в пространстве, тогда и только тогда, когда линия, соединяющая .S с S₂, параллельна линии, которая соединяет Н, с F₂- При помощи задания точекЕи S и линии j и s легко решаются задачи пересечения прямой с плоскостью и двух плоскостей. Этими задачами и кончаются вопросы чистой прямолинейной геометрии, не имеющей дела с измерением линий и углов. Задачи измерительного, или метрического, характера, к которым относится и проведение, перпендикуляров, перспектива не решает просто,—по "следующей причине. При перспективном отображении длины отрезков и величины углов вообще меняются а

Фигура 4.

и меняются непропорционально. Если отре-мок Л В разделен точкой С в отношении АС т

_св=_п, то при перспективе это отношение вообще изменится Ф ; в частности середина отрезка переходит не в середину, а в другую точку. Только сложное отношение четырех точек отрезка А, В, С, D. то есть А В AD

ас ’ во ^сохР^аняется при перспективе (фигура 4а). Для фигур, лежащих в плоскостях, параллельно плоскости чертежа, перспектива дает подобные образы, то есть сохранение углов н сжатие или растяжение длин в определенном отношении (фигура 46). Сложное отношение хотя и не изменяется при перспективе, одиако является слишком громоздким аппаратом для решения простых измеритель

ных задач Н. г. Проще обратиться к таким методам, где величины изменяются в определенном отношении, то есть к методу параллельного проектирования.

2. Параллельная п р о е к ц и я—частный случай перспективы, когда центр О удален в бесконечность, то есть все точки изображаемого предмета проектируются лучами, параллельными нек-рому направлению, на плоскость чертежа. Изображение получается при этом такое, как если бы мы смотрели на предмет из очень большого удаления. Выпуклость чертежа сравнительно с перспективой теряется, но зато законы отображения более просты. На законах параллельной проекции основано построение падающих теней. Действительно, источник света—солнце·—находится от земли на столь большом расстоянии, что практически лучи света можно считать параллельными (если источник света находится на небольшом расстоянии от предмета, тень строится но законам перспективы). Прямые изображаются в параллельной проекции прямыми, кроме тех, которые параллельны направлению проекционных лучей и следовательно изображаются точкой. Параллельные прямые переходят в параллельные на чертеже. Плоскость отображается на всю плоскость чертежа. Проективное соответствие, получающееся при этом между плоскостями, называют а ф ф и н н ы м или аффинитетом; оно характеризуется тем,чтокромелннии пересечения плоскостей, которая сама себе соответствует по точкам, бесконечно удаленная прямаяодной плоскости переходит в бесконечно удаленную прямую другой плоскости (т. к." параллельные переходят в параллельные). Фигура 5.

Это обстоятельство представляет удобство сравнительно с перспективой. Но с другой стороны, в перспективе образы бесконечно удаленных элементов, то есть точки и линии схождения, вместе со следами однозначно определяли положение прямых и плоскостей в пространстве, здесь же образы бесконечно удаленных элементов также лежат в бесконечности и не могут оказать помощи при решении этой задачи. Зато метрич. соотношения в параллельной проекции проще. Длины отрезков на данной прямой изменяются в одном и том же отношении, то есть

АС _ АС’

СВ ~ CB ’

в частности середина отрезка переходит в середину. Длина проекции зависит лишь от направления прямой и направления проекционных лучей, а именно (фигура 5):

.4в Sin а АВ ~ sin (и + β)

Следует помнить, что для разных прямых угол β меняется, так что в разных направлениях длины изменяются в разных отношениях. К о н г р у е и т н о с т ь, то есть сохранение всех размеров фигуры, получается (как подобие в случае перспективы) для фигур, которые лежат в плоскостях, параллельных

плоскости чертежа, и только для них. Этим обстоятельством пользуются при выборе плоскости чертежа, к-рый находится в нашем распоряжении в каждой конкретной задаче, а именно выбирают ее параллельною той из граней фигуры, размеры которой мы хотим получить истинными, неискаженными. Истинные размеры других граней исследуются методом совмещения их с плоскостью,нарал-. [ельною плоскости чертежа. Важным частным случаем параллельн. проекции является т. н. «военная перспектива», то есть параллельная проекция под углом в 45° (а= 45°) к плоскости чертежа, выбранной горизонтально. В этой проекции основания фигур, как параллельные плоскости чертежа, изобразятся без искажения. Кроме того не исказятся длины высот (фигура 6): α= 45°; (5=90°;

AB _ sin 45° J

AB ~ sin 13Ь°

Часто употребляется также параллельная проекция на вертикальную плоскость под

Фигура 6. Фигура 7.

углом 30°. 45° и 60° (фигура 7). Косая параллельная проекция благодаря возможности выбора угла а и плоскости проекции дает чертежи, хотя и худшие, чем перспектива, но все-таки достаточно наглядные. Если отказаться от последнего требования, то простейшей по своим законам и наиболее приспособленной для решения метрик, задач является прямая параллельная, или ортогональная. проекция.

3. Ортогональная проекция— частный случай параллельной, под углом «=90 ц плоскости чертежа, к-рую как правило выбираем либо вертикальной либо горизонтальной. Длина проекции особенно просто выражается через длину проектируемого отрезка: АВ’ =АВ cos β, где β—угол между прямой и плоскостью чертежа. Все точки, лежащие на одном перпендикуляре к плоскости чертежа, имеют одну и ту же проекцию. Определить однозначно по данной проекции форму и размеры фигуры является невозможным. Поэтому либо должен быть даны по крайней мере две проекции фигуры, либо чертеж в ортогональной проекции должен содержать отметки о высотах каждой вершины по отношению к плоскости чертежа. Если плоскость Т—горизонтальна, то высоты над ней считают положительными, а под нею—отрицательными; если Т—вертикальна, то высоты точек, лежащих перед нею, считают положительными, за нею—отрицательными. Т. о. в каждой вершине проекции прямолинейной фигуры должно стоять некоторое положительное или отрицательное число. Высоты остальных точек находим, сое

диняя вершины прямыми. Если фигура не прямолинейная, то нужно знать высоту каждой точки. Принципом отметок (топографии, метод) пользуются при черчении карт. Чтобы изобразить рельеф местности, точки, лежащие на одной и той же высоте, соединяют

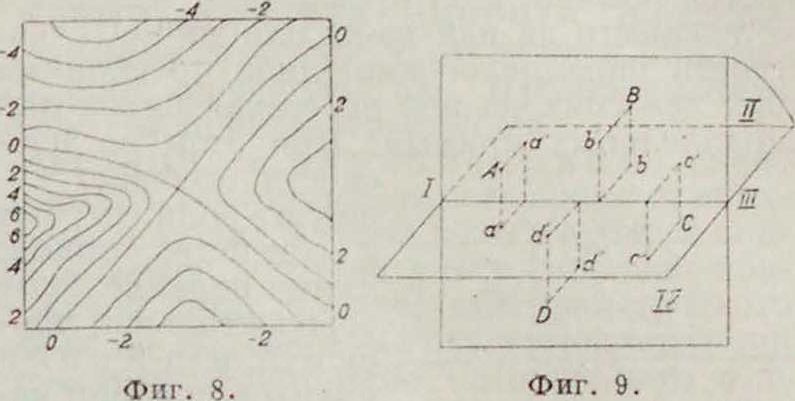
линиями (т. паз. г о р и з о н т а л и, или л и-н и и у р о в н я), которые затем отмечают чи (фигура 8). Однако для многих целей значительно удобнее принципа отметок является проекция на две различные плоскости.

4. Ортогональная проекция на две плоскости изобретена создателем П. г., франц. геометром Монжем (Monge) в 1798 г. За плоскости проекции берем горизонтальную плоскость и вертикальную, выбор которой каждый раз диктуется условиями задачи. При чертежах заданий получается т. о. план и фасад здания. Вместо двух отдельных проекций фигуры Монж предложил изображать обе проекции в одной и той же плоскости след. обр. Вертикальную плоскость врашают вокруг оси проекции (линии пересечения горизонтальной и вертикальной плоскостей) назад до совмещения ее с горизонтальной (фигура 9). Задняя часть горизонтальной плоскости будет совмещена таким обр. с верхней частью вертикальной, а передняя с ее нижней частью. Точка изображается на двойной плоскости двумя проекциями, лежащими на одном перпендикуляре к оси проекции а и а" (фигура 10); при этом расстояние горизонтальной проекции а от оси проекции равно высоте точки по отно-

^[а с-

Фигура 10.

V

шению к вертикальной плоскости, расстояние вертикальной проекции а"—высоте точки над горизонтальной плоскостью. В зависимости от того, как расположены проекции точки, над осью или под осью проекции, можно судить, в каком из четырех квадрантов, на которые разбивает наша пара плоскостей пространство, лежит данная точка (фигура 10). Для определения положения прямой достаточно знать проекции двух ее точек. Соединяя одноименные проекции этих точек прямыми, мы получаем проекции прямой, которые вполне определяют ее положение в простран-,-тве. Соответственные проекции двух параллельных прямых параллельны. Чтобы опре-

делить, пересекаются ли две прямые, мы должны рассмотреть точки пересечения их одноименных проекций. Если эти точки пересечения лежат на одном перпендикуляре к оси проекций, то прямые пересекаются, в противном случае—нет. Плоскость изображается обычно либо проекциями некоторого лежащего на ней тр-ка или мн-ка (в частности параллелограма) либо проекциями двух лежащих на ней пересекающихся или параллельных прямых. При этом на плоскости особенно важную роль играют 2 семейства линий: линии параллельные горизонтальной плоскости. или л и и π п в ьг сот, и линии параллельные вертикальной плоскости, иногда называемые л и н и я м и ф р о н-та. Линии высот вообще пересекаются с линиями фронта; для плоскостей, параллельных оси проекции, оба семейства совпадают. Пара линий но одной из каждого семейства определяет плоскость.

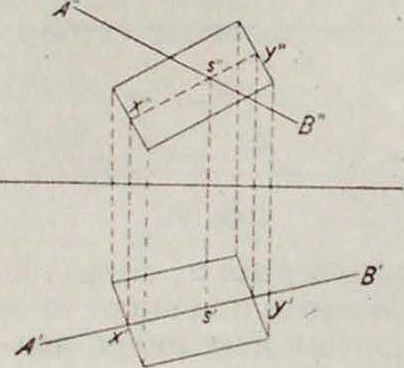
Задача пересечения прямо и и и л о с к о с т и. Для нахождения точки пересечения прямой и плоскости (заданной проекциями параллелограма) проводим через прямую вспомогательную плоскость, перпендикулярную к горизонтальной плоскости проекции. Горизонтальная проекция вспомогательной плоскости совпадает с горизонтальной проекцией АВ нашей прямой (фигура 11). Ищем проекции точек х, у пересечения вспомогательной плоскости с двумя из ребер параллелограма. Горизонтальные проекции х, у этих точек найдутся на пересечении АВ с горизонтальной проекцией па-ряллелограма, вертикальные проекции х", у"—на пересечении перпендикуляров к осп проекции их х, у с вертикальными проекциями этих ребер. Соединяя х" с у" пунктирной линией, мы на пересечении ее с вертикальной проекцией А"В" нашей прямой найдем вертикальную проекцию s искомой точки £ пересечения прямой и плоскости. Для нахождения горизонтальной проекции s достаточно провести перпендикуляр из s" к оси проекции, до встречи его с АВ. Ясно, что построение можно вести, использовав другую вспомогательную плоскость, перпендикулярную к вертикальной плоскости проекции. Результаты обоих построений должны совпасть, на чем и основан способ проверки. Задача пересечения двух 11 л о с к о с т е и сводится к предыдущей. Ищем точки пересечения одной из плоскостей с двумя прямыми другой плоскости и соединяем полученные точки прямой линией. Задача проведения перпендикуляра к данной плоскости. Пи перспектива, ни косая параллельная, ни даже ортогональная проекция не сохраняют величины углов, а следовательно и свойства перпендикулярности. Прямой угол изображается в ортогональной проекции как прямой тогда и только тогда, когда одна из его сторон параллельна плоскости проекции.

Если плоскость задана проекциями линий высот и линий фронта, то перпендикуляр к плоскости (а следовательно и к обеим этим линиям) будет иметь горизонтальную проекцию перпендикулярною к горизонтальной проекции линии высот и вертикальную проекцию перпендикулярною к вертикальной проекции линии фронта. Отсюда простое построение перпендикуляра к плоскости (фигура 12). То же построение в обратном порядке служит для проведения плоскости перпендикулярной к данной прямой. В этом построении и состоит главное преимущество ортогональной проекции перед любой косоугольной проекцией.

Переходя к задачам метрическим, мы встречаемся здесь прежде всего с определением истинной величины отрезка. Если угол а наклона отрезка к плоскости проекции задан, то величину можно вычислить по

А-В

ф-ле АВ=. Но обычно величина угла а неизвестна, заданы лишь проекции отрезка. Поэтому важно иметь геометрич. конструкцию, дающую истинную величину отрезка.

Задача определения истинной длины отрезка. Проекции отрезка Л В меньше истинной величины его, кроме случая параллелизма отрезка и одной из плоскостей проекций. Чтобы привести отрезок в такое положение параллелизма, его вращают вокруг некоторой оси, к-рую выбирают параллельною плоскости проекции. Осью вращения может служить например проходящая через В линия высот h той вспомогательной плоскости, которая проходит через АВ и перпендикулярна горизонтальной плоскости проекции. Горизонтальная проекция h линии h (фигура 13) совпадает с горизонтальной проекцией АВ нашего отрезка, вертикаль

ная·. 12. Фигура 13.

ная проекции h" параллельна оси проекции. Вспомогательную плоскость вращаем вокруг h до тех пор, пока она попадет в положение, параллельное горизонтальной плоскости. Горизонтальная проекция (А) точки А в новом положении будет лежать, как легко видеть, на перпендикуляре к ВА в точке А, на расстоянии А(А), равном расстоянию от точки А" до h". Пунктирная линия В(А) дает истинную величину АВ.

5. Ортогональная аксономет-р и я—ортогональная проекция натри взаимно перпендикулярные плоскости. Точка, как известно из метода координат (смотрите), вполне определяется такими тремя проекциями. Для изображения всех трех проекций на одной и той же плоскости чертежа проектируют· их вместе с осями координат на эту пло-

Фигура и.

(кость косоугольно. По теореме Польке, любая тройка отрезков на плоскости ΟΧ, ΟΥ, ¹ >Ζ таких, что не все четыре точки О, X, Υ, У. лежат на одной прямой, есть нек-рая косоугольная проекция трех единичных (длины 1) отрезков осей прямоугольных координат в пространстве. Поэтому тройку отрезков, координатный триэдр, можем выбрать произвольно, под любыми углами и любой длины. После этого изображение фигуры производится так, как это делается в аналитич. геометрии, то есть по координатам точек. Выбор координатного триэдра дает

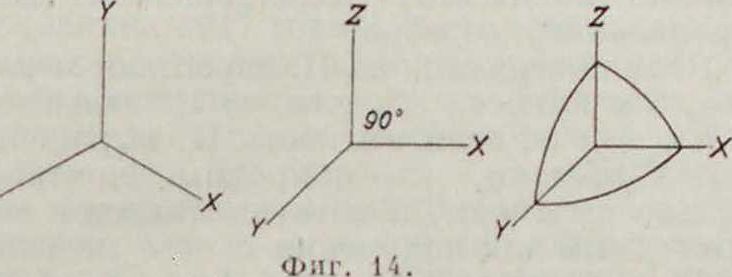
нам относительную единицу масштаба на каждой из осей, так что и обратно—по данным проекциям можем определить координаты точки. Выбор триэдра дает кроме того перпендикулярные направлении на каждой из координатных плоскостей, что представляет большие удобства при построении перпендикуляров. Аксонометрии дает при весьма простых средствах наглядные чертежи, поэтому при всех рабочих чертежах именно она и употребляется. На фигуре 14 даны наиболее употребительные триэдры и аксонометрии. изображение поверхности шарового сектора.

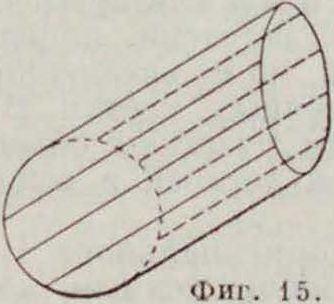
Круг и конические сечения. При перспективе любое конич. сечение может перейти в любое другое. В этом можно убедиться, помещая центр перспективы в вершину конуса (смотрите Конические сечения, фигура 1). При параллельной проекции конич. сечения переходят в одноименные. Действительно, строя на данной кривой цилиндр (косой или прямой), всякую проекцию ее мы получим как сечение цилиндра некоторой плоскостью, непараллельной образующим цилиндра (фигура 15—эллиптич. цилиндр). В частности параллельная проекция круга есть

0

Фигура 16.

эллипс. Желая получить проекцию сферы (поверхности шара), мы только в сечениях, параллельных плоскости чертежа, можем изображать круги, в других сечениях—эллипсы (фигура 16). При параллельной проекции сохраняется свойство сопряженности; в частности пара взаимно перпендикулярных диаметров круга переходит в пару сопря-женных диаметров эллипса. Н. г. находит применение гл. обр. в техническом черчении.

Лит.: Па.льшау А., Начала начертательное геометрии, 9 изд. Мосина—Ленинград. 1927; W <-Ь er II. u. We 1 Is t ei n J., Энциклопедии эле

ментарной математики, 2 над., т, 2, кн. 1, Одесса 1913; S а 1 к о w з к i E., Grimdzijge d. darstellenden Geometric, Leipzig, 1928; Scheffers G. Orund-ziigc der darstellenden Geometric, 2 Auflage, В. 1—2. Berlin, 1922—27. Ю. Рожансная.