> Техника, страница 64 > Неизменяемость геометрическая

Неизменяемость геометрическая

Неизменяемость геометрическая,

неизменяемость системы, свойство стержневой системы сохранять свою те оретическую схему и взаимное расположение отдельных частей в пределах упругих деформаций, вызываемых нагрузками. Стержневые системы с жесткими узлами не изменяемы по существу конструкции своих узлов, например жесткая рама (смотрите); стержневые системы с шарнирн.соедине-ниями узлов, например фермы (смотрите), требуют особого определения своей неизменяемости. Всякую систему молено рассматривать как состоящую из ряда стержней и неизменяемых дисков (смотрите Система). По условию статической определимости число полных шарниров S в системе и число п стержней или дисков должно удовлетворять условию n=2S — 3 (смотрите Система). Если число стержней η <25-3, то система заведомо изменяема. Но и условие n=2S-3 и n > 2S — 3 (система статически неопределима) не гарантируют неизменяемости системы; например показанная на фигуре 1 система, в которой 8= 8 и п=14, то есть 14 >2-8 — 3, по своему образованию является изменяемой. Простейшими образованиями системы являются соединение двух дисков шарниром и стержнем (фигура 2а), или, что то же, присое-

8 6

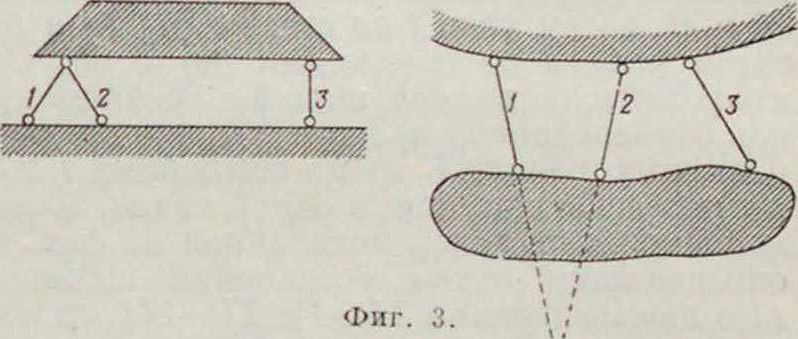
динение узла двумя стержнями (фигура 26), и соединение двух дисков тремя стержнями, не пересекающимися в одной точке (фигура 3 а и б). Последующее развитие системы делается путем присоединения к исходной неизменяемой системе новых дисков, узлов и систем одним из указанных выше" способов; например на фигуре 4 показана комбинированная

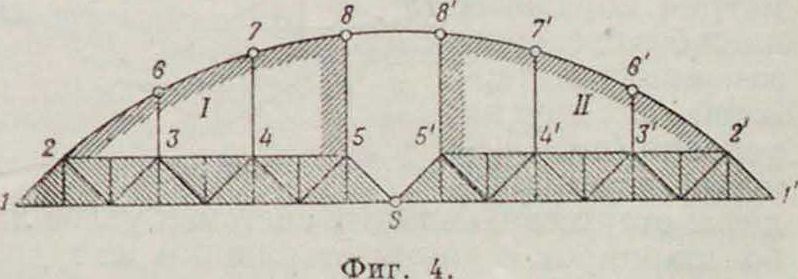
система, неизменяемость которой можно проследить следующим образом по ее образованию. Фермы!—2—5—S иS—5—2’—V как образованные из тр-ков представляют собой неизменяемые диски;к ним присоединены узлы С, 7, S двумя стержнями каждый: узел 6 стержнями 2—6 и 3—б, узел 7—стержнями 6—7 и 4—7 ит. д., чем образуются

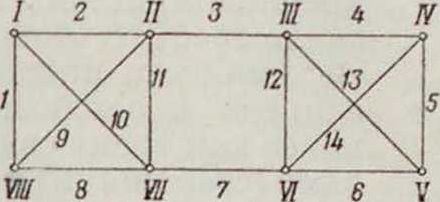
Фигура 1.

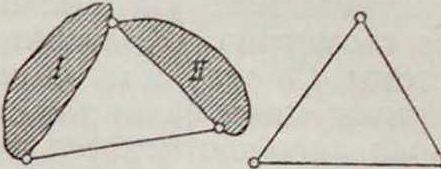
а б

Фигура 2.

Т. Э. 771. XIV.

НЕИЗМЕНЯЕМОСТЬ ГЕОМЕТРИЧЕСКЛЯ

όΰ,

жесткие диски 1 и II; оба эти диска соединены между собой стержнем 8 —8 и шарниром S, что приводит к неизменяемой системе в целом. Аналогично неизменяемость прикрепления системы к земле требует, чтобы система была присоединена к земле не менее как тремя связями (стержнями), не пересекающимися в одной точке (наличие шарнира в присоединении рассматривается как две связи). По существу этого закрепления система и земля должны рассматриваться как два диска.

Указанные условия образования простых систем позволяют проверять неизменяемость системы или указанным путем просмотра ее геометрии, образования из исходной системы (диска) или обратным путем, то есть приведением заданной системы к исходной; последнее достигается путем последовательного устранения из системы узлов с двумя сходящимися в них стержнями,что в силу из-

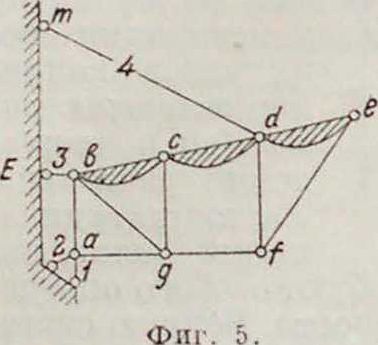
ФИГ. 6.

ложенного не нарушает неизменяемости ос-тающейся части системы. Например проверка Н. г. системы, показанной на фигуре 5, м. б. сделана устранением узла е со стержнями ed и е/, затем узла со стержнями fd и fg, затем узла d со стержнями dm и dc, что приводит к диску cgab, явно неизменяемому, как образованному из двух тр-ков и прикрепленному к земле Е тремя стержнями 1.2,3, не пересекающимися в одной точке. Неизменяемость системы, показанной на фигуре G, определяется путем устранения шарнира 11 с двумя дисками 11—1 и II—III, затем, после устранения шарнира VI с двумя дисками VI—VII и VI—V, приводим к системе, образованной из двух дисков 111—IV и V—IV, соединенных шарниром IV и стержнем аЬ (земля с неподвижными шарнирами а и b). Такая простая поверка Н. г. систем возможна только в тех случаях, если сама система построена простым геометрии. образованием без введения заменяющих стержней и других условий (смотрите Система), что приводит к отсутствию в таких системах узлов либо шарниров с двумя стержнями или дисками (фигура 7, 8, 9 it др.).

В таких системах поверку неизменяемости следует производить, пользуясь условиями кинематики. По одному из них относительное смещение трех дисков возможно только в том случае, если три относительных мгновенных полюса этих дисков лежат на одной прямой (смотрите Кинематический метод). По этому условию система, показанная на

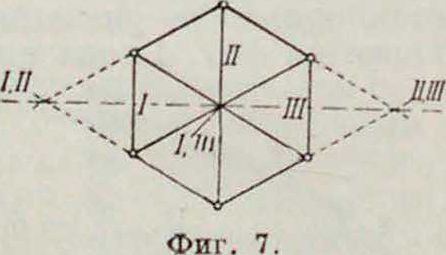
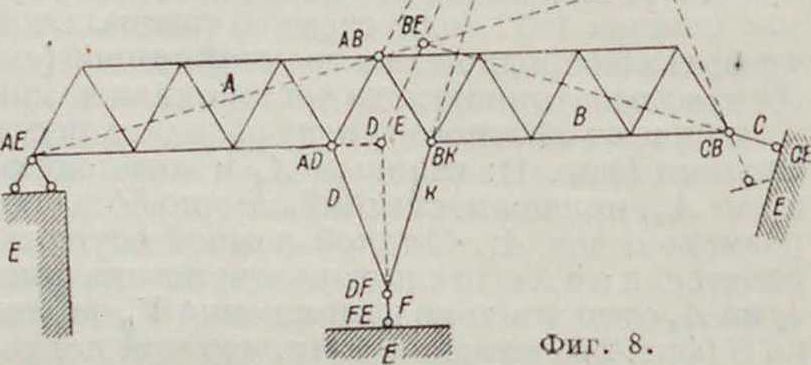
фигура 7, будет изменяема, т. к. относительные мгновенные полюсы I-I1, 11-111, Ι-Ill ее стержней I, II и III лежат на одной прямой. Система, изображенная на фигуре 8, будет изменяема, так как мгновенные полюсы DE, BE и BD, относящиеся к трем дискам:

Е—земля, Ώ—стержень и В—ферма, лежат на одной прямой DE—BD; но достаточно тол i,ко из

fBO

S£

менить направление опорного стержня С, что вызывает смещение полюса BE с прямой DE—BD в точку ВЕ, и система станет неизменяемой.

Исследование неизменяемости путем определения мгновенных полюсов нередко приводит к очень сложным построениям, почему целесообразнее пользоваться другим условием кинематики—построением плана скоростей (смотрите Кинематический метод). При определении этим способом внутренней неизменяемости системы из нее выделяют один из стержней или дисков, действие которого на остальную систему заменяется силами×(фигура 9). С устранением стержня или диска система получает возможность смещения узлов, что позволяет построить для нее план скоростей, обозначенный на фигуре 9 цифрами

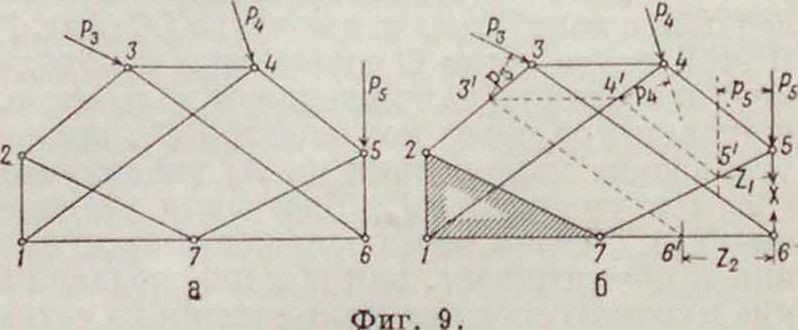
со значками « ». Для построения плана. диск 1-2-7 (фигура 96) принят неподвижным и относительно его определены изображающие точки плана (смотрите Кинематический метод) по исходной скорости 3—3. Если при построении плана скоростей не получится фигура, подобная фигуре исходной системы (фигура 9), то система неизменяема. При получении подобной фигуры выражение возможной работы приводится к виду:

ΣΡρ ΪΡρ

^Λ “ζ,-ζ,” о ^=О0>

что указывает на невозможность установить равновесие, то есть указывает на изменяемость системы. Ндг фигура 10 путем построения плана скоростей определена неизменяемость системы относительно ее опорных закреплений. Для этого в системе устранена опорная связь А5, и для оставшейся части системы построен план скоростей относительно неподвижного шарнира В по принятой скорости 2—2 узла 2, что приводит в конце построения к изображающей точке 5. В виду того что опорное закрепление А5 допускает только горизонтальное смещение узла 5,

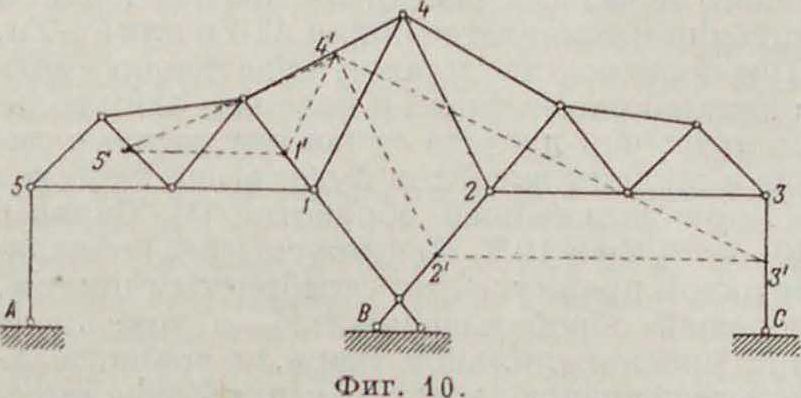
при котором вектор скорости должен быть нормальным и плоскости подвижности, го получение вектора 5—5 в наклонном положении, не удовлетворяющем условию закрепления, устанавливает неизменяе.мость системы

Наконец определение неизменяемости системы м. б. сделано аналнтич. путем. Как известно, усилия во внутренних стержнях и опорных связях системы определяются рядом канонич. ур-ий, из которых величина каждого из усилий×в стержне или в опорной связи м. б. представлена отношением де-термннанто.×= D_p:D. В детерминант D_pвходит столбец с известными членами из канонич.уравнений, определяемыми величиной нагрузки. Если нагрузки на системе нет, то очевидно D_p= 0 и Х=0. Это приводит к условию, что если при отсутствии нагрузки усилия в системе явно равны н у л ю, то она неизменяема. Напр. в системе, показанной на фигуре 11, из выражения момента относительно узла 4 при разрезе системы сечением s—s видно, что усилие в стержне 2—2 равно нулю, что приводит к тому, что усилия в стержнях 2—8, 2—3 равны нулю. Из разреза (— I в той же системе по условию проекции на вертикальную ось следует, что <х>_иг. ц. вертикальнаяслагающая V_a опорной реакции равна нулю. Из выражения момента относительно опорного шарнира 5 следует, что HZ— 7₀1=0, откуда Я=0; это позволяет установить равенство пулю усилий во всех остальныхэлементах системы, чем устанавливается ее неизменяемость. Если бы опорные шарниры лежали на одном уровне, то по ур-ию HZ-V_al=Q нельзя было бы утверждать, что Н= 0, т. к. в этом случае Z= 0; это указало бы, что система изменяема.

Лит.: Прокофьев И., Теория соорушеппй, i. 1. М., 1926; Т и м о ш е и к о С., Статика сооружений, 2 изд., ч. 1, Л., 1926; Мюллер-Бреслау Г., Графин, статика сооружений, пер. с нем., 2 пзд., т. 1, СПБ, 1908. И. Прокофьев.