> Техника, страница 65 > Номография

Номография

Номография, совокупность метод в графич. построений, выявляющих данные функциональные зависимости переменных друг от друга.Совокупность геометрических элементов (отрезков, точек и тому подобное.), служащих для определения функциональной зависимости переменных, называется номограммой, или абаком. В зависимости от того, располагаются ли все элементы номограммы на некоторой кривой (в частности на прямой), плоскости или в пространстве, номограммы бывают линейные (прямолинейные), плоские и пространственные. По характеру геометрия. элементов, служащих для построения номограммы, последние состоят либо из системы помеченных точек либо из системы помеченных линий; в последнем случае иногда каждой переменной соответствует свое особое семейство кривых

(прямых), совокупность которых образует т. наз. сетку номограммы. Обычно данная ф-ия переменных может быть представлена как системой точек, так и системой кривых (прямых), причем между ними существует нек-рое однозначное соответствие. Рассмотрим в качестве примера следующий случай. Пусть имеется ур-ие:

(1)

^ж + ^=1 15 ^τ 20

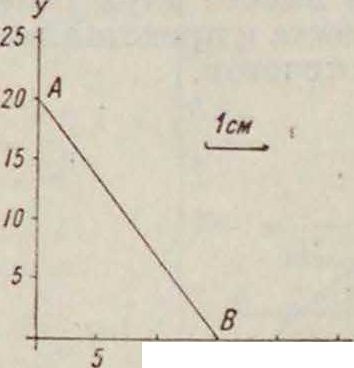
В прямоугольных декартовых координатах последнее ур-ие представится графически в виде прямой, опекающей на оси аз-ов отрезок, равный 15, а на оси у-ов отрезок, равный 20, причем каждому определенному значению аз, удовлетворяющему (1) и представленному нек-рым помеченным отрезком на оси аз-ов, соответствует нек-рый помеченный отрезок на оси у-ов. Т. о. данный график в декартовых координатах представляет собою номограмму, состоящую из системы помеченных отрезков прямой. Вместо осей аз-ов и у-ов можно однако взять две параллельные прямые ξ и у с нанесенными на них делениями, так чтобы прямая ξ соответствовала оси аз-ов, а прямая η оси у-ов. Тогда точке А на оси у-оз (фигура 1), имеющей ординату 20 и абсциссу 0, соответствует на фигуре 2 прямая αα, соединяющая деление 20 прямой у с делением 0 прямой f; точно так же точке В, находящейся на оси ж-ов (фигура 1), соответствует прямая ЬЬ фигура 2. Таким обр. всей прямой АВ фигура 1 соответствует точка (ab) на фигуре 2, получившаяся о г пересечения прямых аа и ЬЬ. Нетрудно видеть, что точкам, лежащим на одной и той же

W 15 20 25

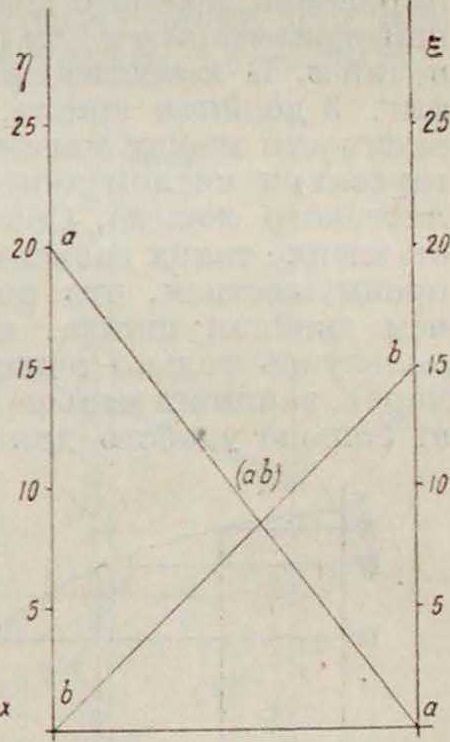
фигура 1. Фигура 2.

прямой фигура 1, соответствует пучок прямых, проходящих через одну и ту же точку на фигуре 2, и что параллельным прямым фигура 1 соответствуют на фигуре 2 точки, расположенные на прямой, параллельной прямым ξ и η. Т. о. для данной системы помеченных отрезков может быть построена соответствующая система помеченных точек, и наоборот.

На практике чаще всего применяются графики, построенные в декартовых координатах, то есть применяющие систему помеченных отрезков. В технике особенно часто этот способ применяется в тех случаях, когда аналитич. выражение функциональной зависимости переменных неизвестно,

а дана лишь экспериментальная зависимость нек-рых частных значений переменных; таким способом вычерчивается наир, кривая намагничивания в электротехнике, кривая JS в термодинамике и т. д. В Н. однако применяются также и другие методы графич. представления функциональной зависимости переменных друг от друга. Так, для ф-ии у=f(x) помимо обычного представления ее в виде кривой в декартовых координатах м.б. применен еще и следующий способ графич.

Лмп витки taycc

-гоооо

2600

2000

1500

1000

5 00 250

100

50

25

го то ГС PaiM Sci.

4000

то

12000

10000

1000

6000

то изображения. Взяв произвольную прямую х и нанеся на нее в данном масштабе ряд натуральных чисел, получим т. н. натуральную ш к а-л у. Отметив затем у каждого деления соответствующее числовое значение переменной у, получим т. н. двойную шкалу, которая и представляет графически данную функциональную зависимость у от х. При помощи интерполирования можно с достаточной точностью найги значения у и для промежуточных значений х. В качестве примера приведена на фигуре 3 двойная шкала, определяющая зависимость между магнитной индукцией (в гауссах) и числом ампер-витков на сантиметров для листового железа. Обычное графич. представление таких зависимостей обладает тем преимуществом, что оно более наглядно, чем двойная шкала, но зато последняя, пользуясь только одним вместо двух размеров, занимает меньше места и представляет больше удобств для отсчетов.

ISO-	- !0 -	-I.SS
	- з -	-1,50
по-	- 8 -	-1,60
	L 7 -	-1.61
160-	|-е ·	1.62
iso-	• 5 -	1.65 ш
140- 150-		-1,65
	з -
120-	2 -	-1.70
ПС: wo-	-	1.75
во-		-ф

Фигура з.

Фигура 4.

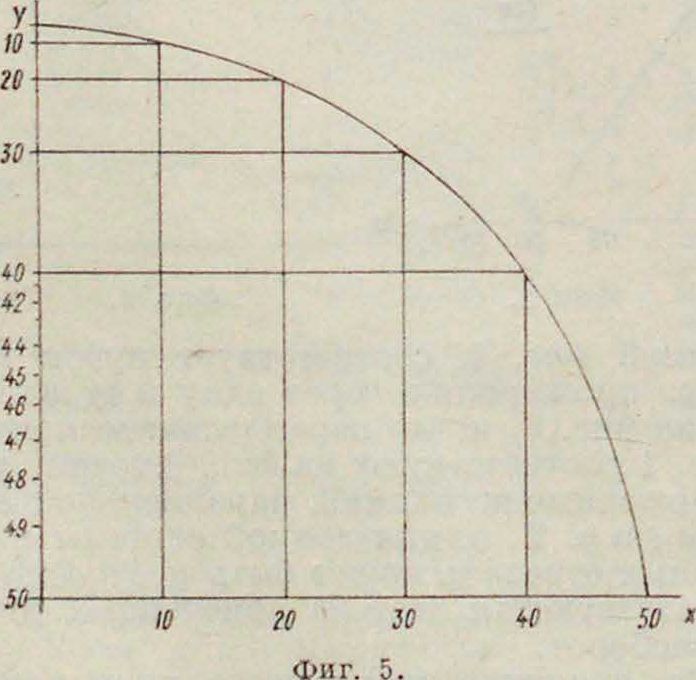
Если имеются две функции одной и той же переменной ху=f_x(x) и г=f₂(x), то аналогичным способом можно построить тройную шкалу. На фигуре 4 приведена например тройная шкала, выражающая взаимозави симость давления насыщенного пара воды (в atm), его темп-ры (в °С) и его энтропии (в абс. единицах). Пусть имеется кривая у=f(x), построенная в декартовых координатах (фигура 5). Если на оси у-ов нанести деления,соответствующие натуральным значениям ж, не нанося значения у, то получится т. н. функциональная шкала. Если затем на последней нанести еще и соответствующие значения у, то очевидно получится двойная шкала. Деления обычной логарифмич. линейки представляют собой функциональную шкалу. Модуле м, или масштабом, у(у) функциональной шкалы у=/(ж) называется число единиц длины (мм или см), содержащихся в отрезке, соответствующем единице переменной у. Наиболее часто встречающиеся и в то же время наиболее важные функциональные шкалы суть шкалы п о-тенциальные, логарифмические и проективные. Потенциальную функциональную шкалу, представляющую функциональную зависимость у=х^п, где п—целое или дробное число, можно построить, либо пользуясь графич. построениями в декартовых координатах с логарифмич. делениями (смотрите Логарифмические диаграммы) либо при помощи таблиц и непосредственных подсчетов. Логарифмич. функциональная шкала, особенно часто применяемая на практике, представляет собой функциональную зависимость у= lgx. На фигуре 6 представлена логарифмич. функциональная шкала с модулем у(у)=40 лш. Построение проективных функциональ- ’ ных шкал основывается на следую- _{фиг 6}щих началах. Пусть имеются на прямой d_x точки А, В, С_х, D_x и на прямой d₂точки А_г, В, С₂, П₂, причем пусть имеет место равенство го

П.5

1.15

1.5

AiCi. Афх

BiG’i Hi-Di

Ач(^2. A 2D2 Ii2.C2 *

(2)

Обусловливаемая этим равенством зависимость точек называется проективной. Графически проективная зависимость м. б. получена следующим образом. Передвинем совокупность точек А_г, В_х, С_х, D_x по d, и совокупность точек А₃, В₂, С₂, D₂ по d₂ до совпадения точек А_х и А₂ с точкой пересечения прямых d_x и do. Взяв затем произвольную точку Р, называемую центром перспективы, нетрудно усмотреть, что прямые РВ_Х, PC_X,PD, пересекут при их продолжении прямую d₂ как раз в точках В₂, С₂, 73₂, удовлетворяющих соотношению (2).

Если на прямой d_x взять начало отсчета О_х и обозначать отрезки О_хА_х, О_хВ_х, О_хС_х,. через у_х, у₂, у_я,. и аналогичные расстояния от какого-либо начала 0₂ па оси d₂ обозначать через г_х, г₂, то между соответ ствующими расстояниями у и z существует соотношение:

hz + p

У=у

° mz + η

(3)

где к, р, т, п суть нек-рые постоянные. Отсюда следует, что если на прямой d₂ нанести функциональную шкалу z=f(x) и спроектировать ее из какого-либо центра на прямую d₃, то получится функциональная шкала для ф-ии:

fe/W.±P. ₍₄₎

" тДж) + η

Рассмотрим в качестве примера построение функциональной шкалы для ф-ии

У —

2х-3 * + 1

(δ)

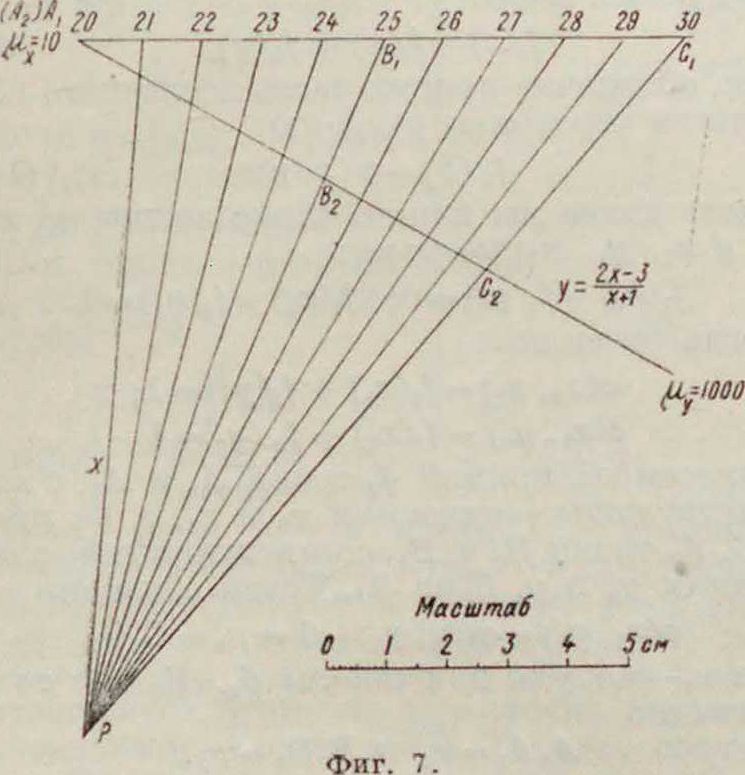
в пределах изменения ж от 20 до 30. Взяв ось ж-ов, нанесем на нее деления с модулем /Ах)=10 миллиметров от 20 до 30 (фигура 7). Возьмем

Для номография, представления ф-ии нескольких переменных применяются часто несколько параллельных функциональных шкал в зависимости от числа переменных. Пусть имеется ф-ия

z*=mx + ny. (6)

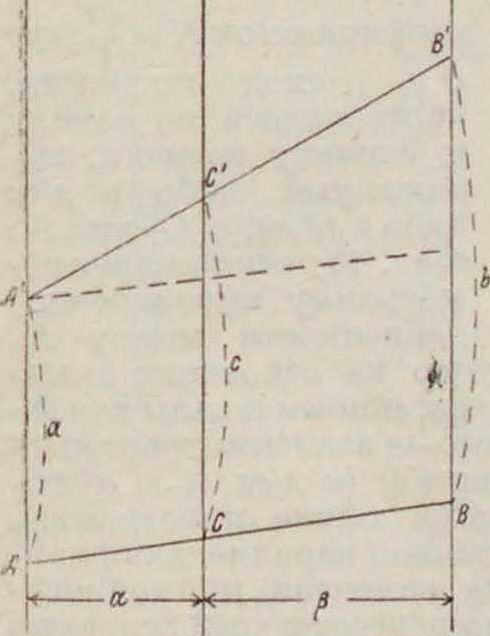
Пусть далее имеются три параллельные прямые ά_Λ, d₃, d₃. которые пересекаются двумя прямыми АВ и АВ (фигура 8а), из которых первую будем считать неподвижною, а вторую меняющей свое положение. Если обозначить расстояние между d_l и d₃ через а, a расстояние между d₂ и d₃ через β, то имеем:

Ь с с —— (ΐ> /*у

β ~ а ’

где а=АА; Ь=ВВ’·, с=СС.

Из равенства (7) имеем далее

a (b - С)=β (С - а) (7)

или

(а + β) с= βα + ab. (8)

Если провести вместо АС какую-нибудь другую прямую, то она отсечет на прямых d_lt d₃. d₃ отрезки, удовлетворяющие равенству (8). Далее, сравнивая равенство (8) с равенством (6), видим, что х и у играют роль а и b, a т и п роль β и а. Если положить

2=(т + п)г, (9)

то получим равенство

(т + n)z=тх + пу, (10)

вполне аналогичное равенству (8), или, разделив на некоторую произвольную величи на этой же оси две произвольные точки, например В (25) и С (30), и найдем подсчетом из (5) соответствующие значения для у, а именно В₃ (1.808) и С, (1,839). Значению же Λ_v (20) соответствует значение А_г (1,762). Таким образом отрезку AJ3_X на оси ж-ов соответствует отрезок 1,808—1,762=0.046 на оси у-ов, отрезку -4,С₁ соответствует отрезок 1,839—1,762=0,077. Проведем через А_х

прямую у И ΟΤΙ ^а‘ “» ложим на ней в определенном масштабе точки

В₂,С₂, определенные вышеупомянутыми величинами. В данном случае удобно взять масштаб д(2/)=1000. Тогда ^Д^ЮООх х0,046=46 миллиметров и Н,С₂= 1000х х0,077=77 миллиметров. Проведя прямые В₃В_г и С_ХС₃до их взаимного пересечения, получим центр перспективы Р. Соединив затем Р со всеми делениями оси ж-ов и найдя пересечения этих прямых с осью у-ов, получим на последней искомую функциональную шкалу.

Фигура 8а.

ну I, определяющую величину масштаба, найдем:

т-гп, 7П, п

z’=_г ж + _t у. (11)

Т. о. для построения номограммы, соответствующей равенству (6) или (10), проведем три параллельные прямые d₃, d_s. d₃, так чтобы расстояние от d₃ до d₃ равнялось а расстояние между d₃ и d₃ равнялось ™. На

* i

прямой d₃ можно отложить как шкалу для переменной г, так и шкалу для переменной г. Т. к. при ж=О, у=0 и г=0, то все три нулевые точки будут лежать на одйой секущей прямой: точно так же и деления 2 бу-ri i j ДУ^Т лежать на од ной прямой, т. к. при ж=1, у=1 и г=1. Что касается переменной г. то так как при z=l, z=m + w, делению 2 шкалы з соответствует деление т + п шкалы г. Таким образом масштаб для z в т + п раз меньше масштаба для г.

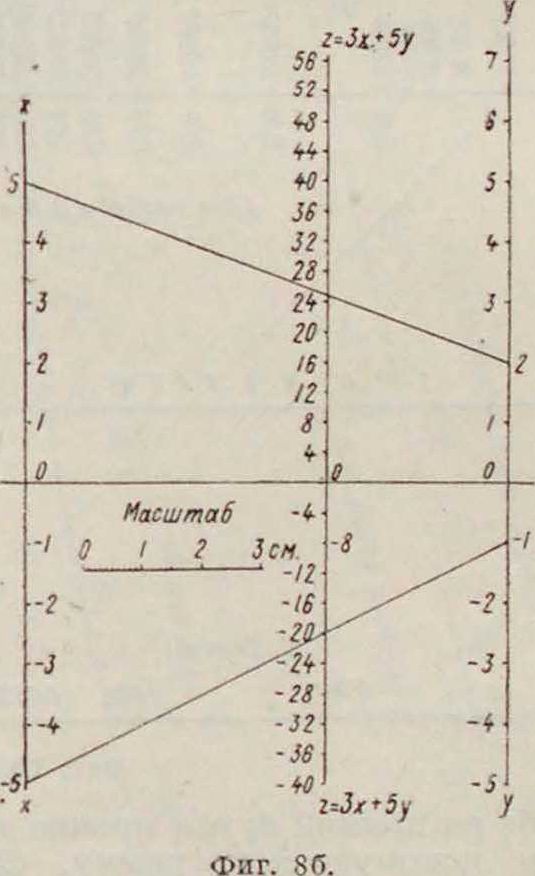
Для примера построим номограмму для функции г=Зж + 5у. Положив z=8z и 1=0.1,имеем 80г==30а:+ 50у. Расстояние между осями d_y и d₃ берем равным 50 миллиметров (фигура 86), а между d₃ и rf₂ равным 30 миллиметров. Модули для шкал х и у берем μ(χΛ=/<(?/)=10 миллиметров. Тогда для z имеем модуль μ(ζ)== 1,25 миллиметров, то есть прямая, соединяющая деления 2 шкал ж и у, будет пересекать шкалу z в точке, соответствующей делению 8. Нанеся в полученном

		а2
1 1-1+
1
1
		С»

Фигура 9.

ном итоге сдвинуть вверх или вниз на величину р.

Однако особенных практических выгод от применения номограмм, построенных длята-ких простых функций, не имеется. Гораздо большее практическое значение имеют номограммы вышеприведенного типа в соединении с функциональными шкалами. Пусть di, d₂, d₃ представляют функциональные шкалы, так что

(¹²>

тогда можно построить номограмму для следующей ф-ии:

/sOO =/ii®) + h(y), (13>

или, обозначив правую часть последнего равенства через ψ (ж, у), ф-ию

/»(*)=<Р(®. У)· (14>

Пусть дат ее мы нашли такие значения х₀, Уо и x_L, у_г, которые дают:

/i(®o)=/г(2/о)=0; /фж,) -=1.

Тогда очевидно

<Кхо. 2/ι)=/iW + /2(2/1)=i; φ(Χι, У о)=/i(3:i) + /2 (2/о)= 1·

Нанесем на прямой d_y точки Л_л и А_и соответствующие значениям ж₀ и ж, а на прямой d₂ точки Б₀ и В_х. соответствующие значениям у_а и у_х (фигура 9). Тогда очевидно

φ(Ρι, Уо)=φ χо- г/ι)=1=д₈=с_ус₀, где //₃—модуль для шкалы d₂. Кроме того очевидно где и μ₂—модули для шкал d_x и d₂· Не-

-ю.ооо	00021-	1Ш0 -16.000 18.000 го.000	000Οί-	00006	1	mil	000Oil·	§§§§	1	трудно что ^3 _
		i	£	егг	<5>	to t4 Q5O1. C5 Qb θ“		«5Г	t-5 s}· ‘O с	И 2 < Отсюда

/1

β

(для расхода О выражен в ^м3/сек)

/2

(15>

и

4 5 6 7 8 9 10

20

Расход О ^л/сек

30 40 50 60 708090ЮО

(10)

.0,0

о.ог 0.03 ojm 0,05 0.06 c.os 0.1 Q= "feeк

/<i _ « _β

μ₂ β *

При расчете каналов круглого сечения приходится часто иметь дело с коэфициентом К=где

Уклон I

0.001

0,002

от о.од *щб о,орв

0,0

Фигура 10.

масштабе на прямой d₃ все прочие деления, получим искомую номограмму. Соединив например точку 5 оси ж-ов с точкой 2 оси у-ов, получим в точке пересечения этой прямой со шкалой z точку 25. Точно так зке, соединив точки ж=— 5 и у= — 1, получаем на шкале z точку с делением —20, и т. д. Для ф-ии z — тх — пу стороны возрастания делений на осях ж-ов и у-ов, в отличие от рассмотренного случая, противоположны. Если имеется функция вида z=тиж + пу ± р, то построение производят точно также, как и выше, но шкалу z следует в окончатель-

Q — расход жидкости, протекающей по каналу в единицу времени, выраженный либо в л/ск либо вм³ск, а г—уклон.

¹ ’ -*· Фигура 10 представляет номограмму, выражающую зависимости между К, Quin построенную на основании вышеприведенных методов, причем шкалы для величин К и Q двойные—в зависимости от двух способов выражения Q (в л/ск и в м³ ск).

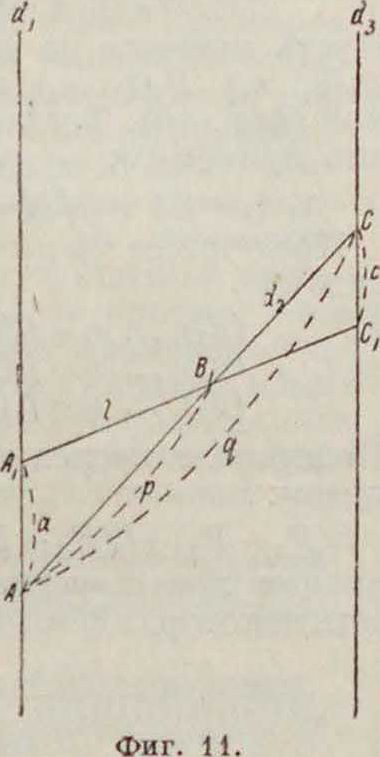
Часто применяются также номограммы, у которых промежуточная параллельная прямолинейная шкала заменена прямолинейной же шкалой, но пересекающей основные шкалы под некоторым углом. Пересечем две параллельные прямые <2, и d₃ (фигура 11) прямою d₂, к-рую будем считать основной прямой, и прямою I, пересекающей первые две прямые в точках А_у и С_ъ а последнюю прямую в точке Β_λ. Тогда очевидно имеем:

Ί р Р

с а

(17)

где АА_Х — а; СС₂*= с;=р; АС=Допустим, что шкала rf₂ — проективная шкала от другой шкалы δ, удовлетворяющей равенству

P-ih’ <¹⁸>

тогда а »_1

a + с <5 + 1

или α(δ + 1)=а + с и с-ад. (19)

Если а=Д(х); д=/*(»); с=/₃(г), то имеем:

/*00=А(ж)Ш)· (20)

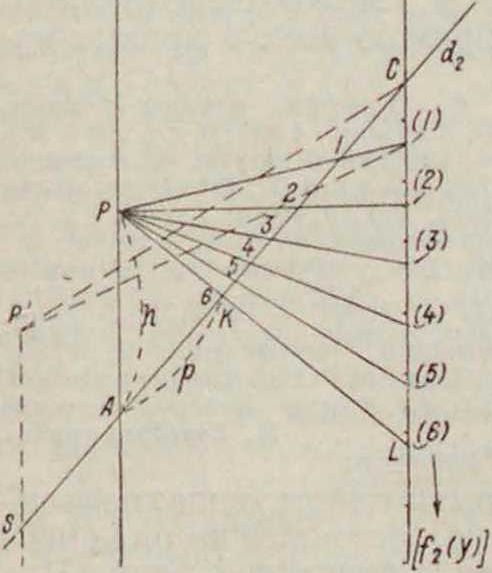
Для определения на da шкалы для р, так чтобы

^ /₂(v) + i’

отложим на d₃ от точки С натуральную шкалу (фигура 12), и пусть P — предварительный центр перспективы; тогда точке С на d₃ соответствует на d₃ точка р=q (т. к. /₂(у)=0 при этом). Проведя из P прямую PS d_a, получим на d₂ точку, которая соответствует f₃(y)=00, то есть точка S должна обозначать деление р=0. Отсюда следует, что SC=q. а т. к. обусловлено, что АС=</, то точки S и А должны совпадать, то есть центр перспективы должен находиться на d_u например в точке Р. Что же касается модулей, то нетрудно доказать, что между ними должно существовать соотношение:

где h=РА,

d,

/*(/*)

причем все модули выражены конечно в одних и тех же единицах длины. В качестве примера рассмотрим построение номограммы для функции г=хУ. (22) Из (22) имеем gz=y gx (23) и. сравнивая(23) с (20), получаем: U(z)-lgz, /i(t)=lg®; /*(»)-»· (2-4) Отложим на ά_Λделения, которые соответствуют lg х, причем пусть /<(Д)=40 миллиметров (фигура 13). На d₃ строим натуральную шкалу для /₂(г/) -ус модулем д(/₂)=16 леи (на фигура обозначения для этих делений взяты в скобках). От точки А, соответствующей делению 1 первой шкалы, отложим отрезок АР_г-h с модулем 8 миллиметров, так что Ιιμ(Ιι)=8 _к.чм.

Фигура 12.

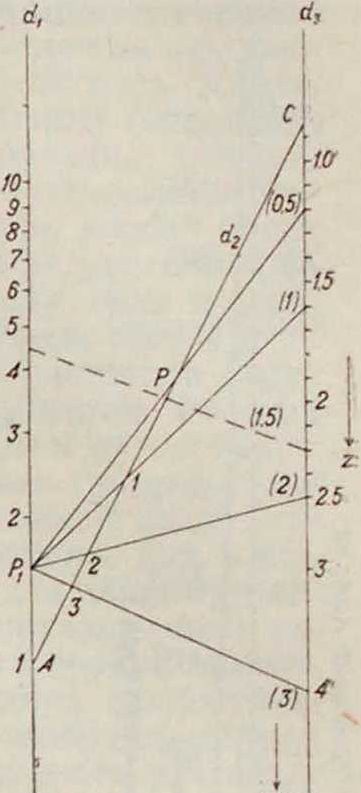
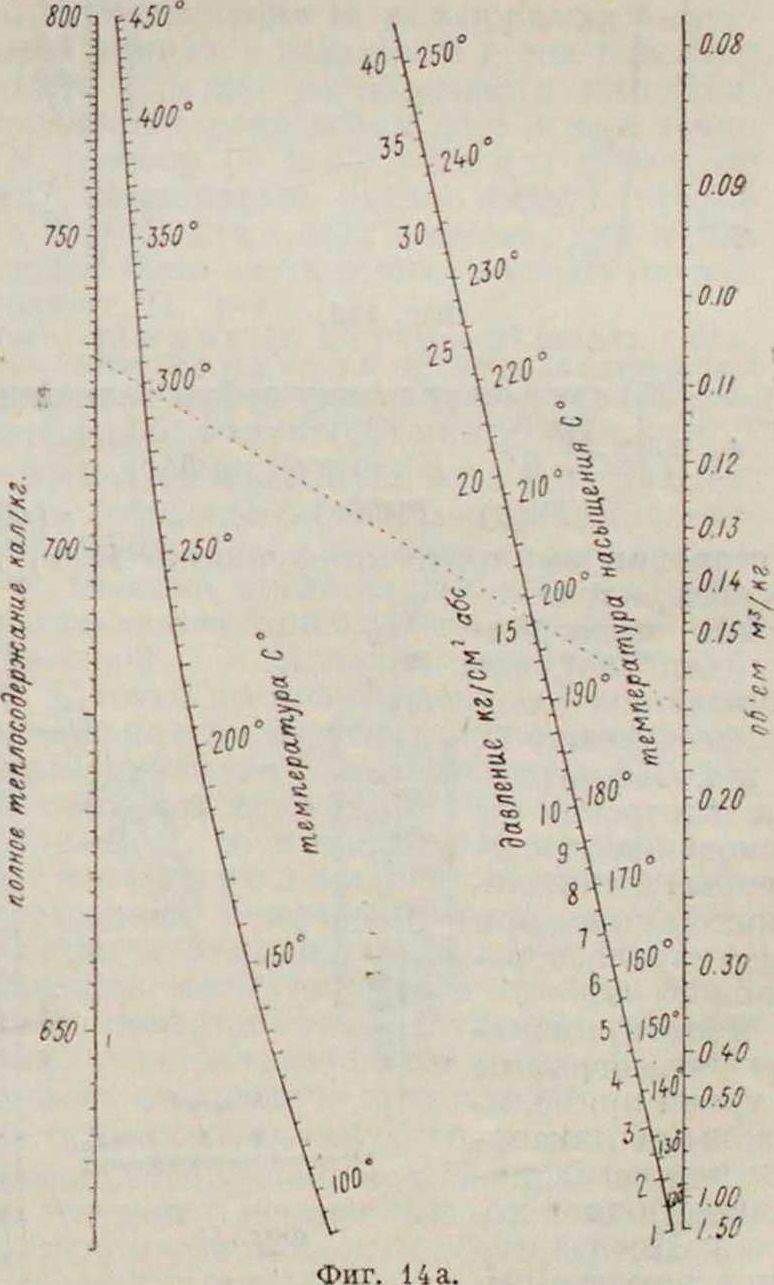
Точку Г, берем в качестве центра перспективы. Проектируя натуральную шкалу у из Р₁ на d₂, получим шкалу для р. Затем на d₃ от точки С откла-дываем деления лога-рифмич. шкалы L(z) в масштабе м(/з) - —— - 80 миллиметров, которые и дадут значения z, соответствующие тем значениям р и х, которые находятся на прямой, проходящей через все три, частные значения. На фигуре 14а и 146 приведены в качестве примера номограммы для водяных паров, построенные по вышеприведенному принципу.

Аналогичными же методами построена на фигуре 15 номограмма для следующего случая. Пусть Р—вес состава движущегося поезда, Р"—вес парово- фигура 13.

за, Р-Р + Р" — вес всего поезда, г—уклон пути (тангенс угла наклона), К—сила тяги паровоза, R и И"—

сопротивления передвижению на единицу веса состава и паровоза. Тогда имеем

F - P (R + i) + P"(R" +г). (25)

Для данного поезда Р"—величина постоянная. a F, R и R"—переменные, зависящие от скорости V поезда определенным, устанавливаемым эмпирически, образом, так что

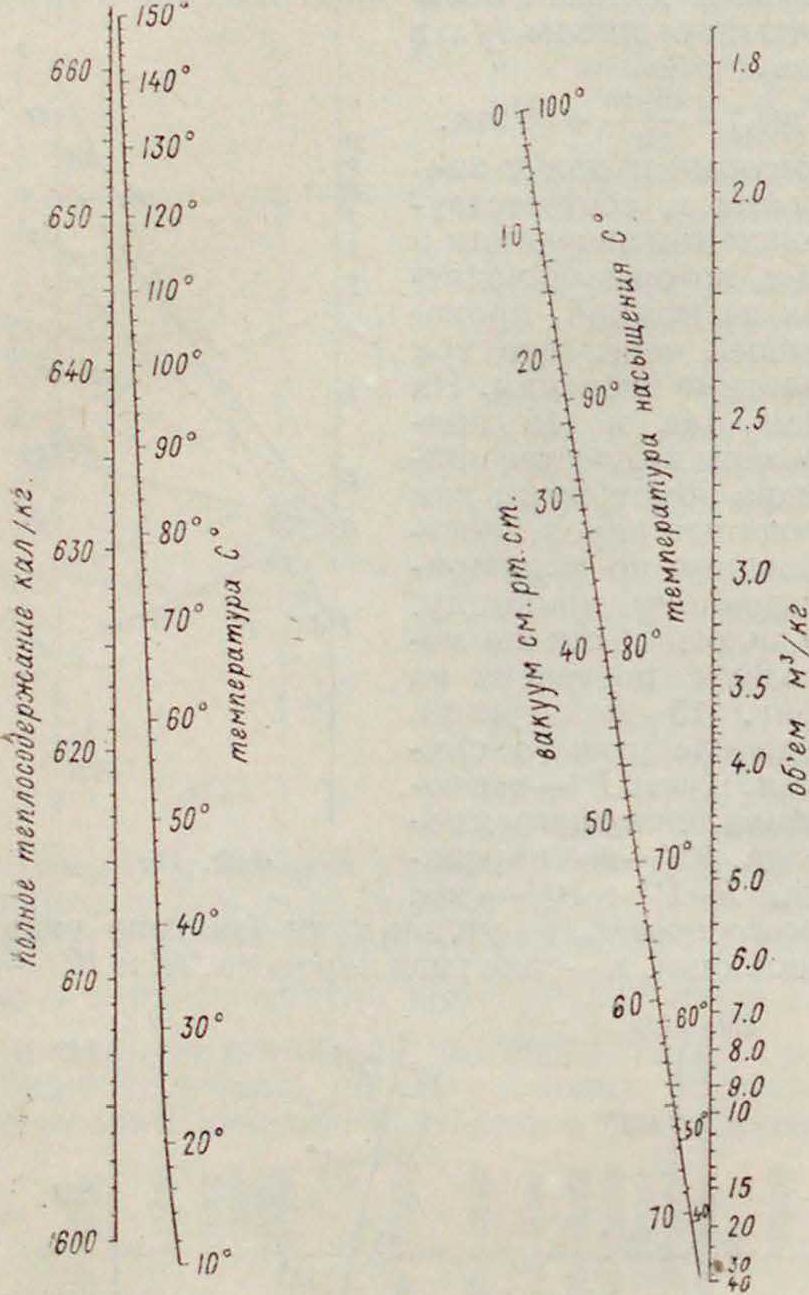
Фигура 146.

ур-ие (25) связывает между собою величины Р", V, г. Из ур-ия (25) имеем, обозначая F — P"(R" — R)=F(v) и R » Φ(ν),

(26) F(v) и

№ s Ш § Μ Ί ISO <3

F(v)=Ρ[φ(ν) + г].

Установив эмпирически функции Φ(ν), можно пост- _ароить номограмму для (26), вы- ³⁰ ражающую зави- т симоеть между Р, ц,_/0V и г. Номограм- | ма построена на -основании опреде-1¹³⁰ ленных эмпириче- *^м ских данных, при,® * весе паровоза, ра-1 % в ном 25 тонн ^ Μ

Часто примени- » ют номограммы с тремя прямолинейными шкалами, пересекающимися в одной точке. Последнего типа номограммы применяются для графического изображения функций следующего вида:

—ί_ - -А—i—. (27)

/з(*) /iW. Ыы>

Масштаб 2 J

Фигура 15.

2i

k

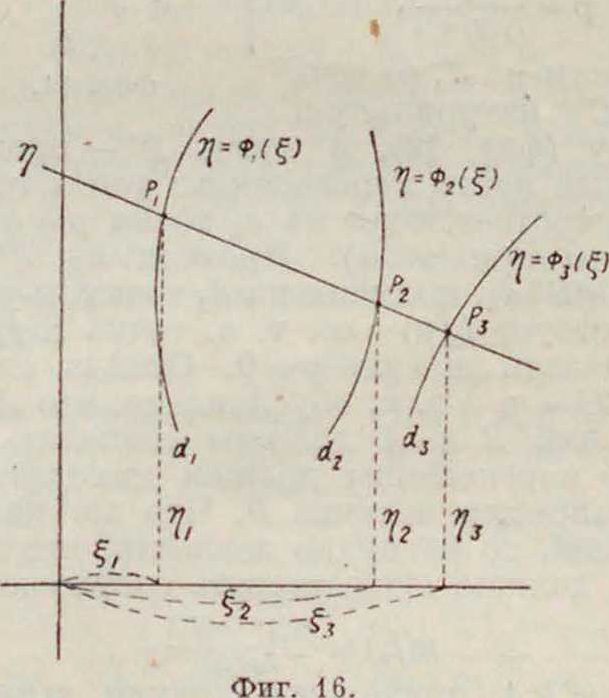
Во многих случаях является более целесообразным применять криволинейные шкалы вместо прямолинейных. Пусть имеются три кривые d_lt d₂, d₃, ур-ия которых в декартовой системе осей координат ξ, η будут:

i(l); η - ФШ V - φ₃(ξ). (28)

Пусть имеются на кривых точки Ρ_ι(ξ_ι. >7,); -Polia- %); Р₃(1з- %). лежащие на одной прямой (фигура 16). Тогда имеем аналитич, условие для этого:

Vi (ii — ia) + ⁷h(sз ^— !ι) + ⁷k(ii ~ i’2) =“ 0. (29) Представим ур-ия (28) в параметрическом виде:

(А) -·- П - ξ - F_t0c)

(А) ·· v-Ш·, $=Fi(y) · (30)

(А). Ч-/.(*); i - W ) Подставляя последние ур-ия в условие (29), имеем:

/i(F, - F*)+UF₃ - Fi) + UF, - F_a)=0, (31) причем левая часть последнего равенства есть некоторая ф-ия ψ(χ, у, г). Так. обр., если

имеется ф-ия трех переменных х, у, г, к-рую можно привести к виду (31), то можно построить номограмму для зтой ф-ии таким обр. чтобы соответствующие частные значения переменных х, у, ζ можно было отсчитывать на сечении прямою всех 3 кривых номограммы.

Лит.: Блох Л. С., Графит, методы техник, расчетов (номография), Харьков, 1929; II и р а п и М. Методы графит, изображений в науке и технике, Берлин—Рига, 1923,L а с ш а η η О ., Die Herstellung gczeichneterRechentafeln, Berlin, 1923; Lu с k e у p., Kinfiihrung in die Nomographic, T. 1—2, Lpz u. В. 1918—20; Pirani 11, Die graphische Darsteilung in Wissenschaft u. Technik, li. 1 922; S c h in i d t Th. Darstellende Geometric, 2 Aufl., li. 2, Berlin, 1923; Schwerdt H., Lehrbuchd. Nomographic, В. 1924; Werkmeister P., Das Entwerfen von graphischen Kechentafeln, B., 1923; CM. также Логарифмически’·, диаграммы. M. Серебренников.