> Техника, страница 67 > Определители

Определители

Определители ,детерминанты, алгебраические суммы, образованные по особому правилу из каких-нибудь и² количеств (чисел, независимых переменных, функций и тому подобное.); такого рода суммы часто встречаются в различных отраслях математики, поэтому для этих сумм введено и особое название ίι схематнч. обозначение, удобное для запоминания, преобразованийи вычислений.

Возьмем систему например трех ур-ий с тремя неизвестными:

а_хх + b_xj + c_Lz=άΛ

а₂х + Ь_гу + c₂z=d₂ · (1)

а^х + b₃y + c₃z=d₃)

Решение:

х =

У =

dib₂c₃ — d i b ₃с₂- - d₂b ₃ci — d₂b C₃-l· d^b C₂ — d₃b₂C (l b₂c$ — Οχ 63C2+ а2Ьз^с1 ” ^α2^1^Γ3 +^α3^ l^c2 ~ ^₃b₂Ci * _Qi ^2^сз ~ ^ai d$c₂- -(i₂d₃C — u₂d}C₃ +a₃d C₂ —ci₃d₂Ci

&ib₂c₃ — (iib₃c₂-{ a₂b₃< 1 — iC;_{-ba361C2 — ci₃b₂C

Я] b₂d₃ — a 1 b₃d₂ -* a₂b₃di —CL₂b d₃·l·(^₃b]d₂ — a_лb₂dι

(2)

aif>2^c3 ^—Ч163С2 +aai>3^ci ^— игА^з + o₂bjC₂~ Q₃b₂C

В выражениях (2) для неизвестных х, у и z знаменатели одинаковы, числители же, как легко заметит!», получаются из знаменателя через замену коэфициентов, при определяемом неизвестном, количествами правой части ур-ий. Алгебраич. суммы, стоящие в числителе и знаменателе ф-л (2), и являются определителями. Следуя общепринятому обозначению для О. (Cayley), записывают например знаменатель в выражении (2) так:

«! ?>! Ci

а. Ь₂ с₂а₃ Ь₃ с₃

Про О. (3) говорят, что он образован из трех горизонталей и трех вертикалей, и называют О. третьего порядка. Итак имеет место тождество: а, !?1 с,

(3)

А Со а. b. с_я

= α^₂ο₃ — а_лЬ₃с_г + а._гЬ_яс_л — ci₃b_ic₃ A H3biC₂ с3^2^ι · (4)

Девять количеств, записанных схематически в левой части тождества (4), называются элементами О., а шесть слагаемых правой части—ч ленами О.

Укажем нек-рые применения О. третьего порядка.Площадь тр-ка с вершинами^,?/!),

(ж₂, У г)» (^хзу У г)¹³ прямоугольной системе координат равняется:

, Х Vi 1

о Уа 1

2/з 1

Ур-ие прямой, проходящей через две данные точки (x_lt у у) и (х₂, |/₂):

i у 1 *ι 3/ι 1

Хя 2/а 1

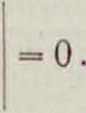
Л-а

X By В_г

В векторном исчислении векторное произведение [АВ] выражается О. 3-го порядка: i i к [АВ] — Л*

В_х

где А_х, А_у, А₃ и В_х, В_у, В_г —проекции соответственно векторов А и В на прямоугольные оси координат, a i, j и к—единичные векторы на тех же осях. Механика, трактующая свое содержание на базе векторного исчисления, пользуется О. 3-го порядка; например момент Л силы F

M=[rF]~· х секториальная скорость

J

У

к г

F,

к г

V,

линейная скорость в зависимости от угловой и выразится так:

i j к

V=[«»·]=и_т и„ и, и тому подобное.

У

В тензорном исчислении удобно пользоваться схемой записи О. 3-го порядка, наложив нек-рые ограничения при преобразованиях с О. Так, тензор Т, имеющий составляющими о„ Ь_и св а₂, Ь₂, с₂; а_а, Ь„. с₅, представится в виде условного равенства

Т =

обратный тензор

Т~1 =

а₁ Ь₁ Су «₂ h п с., «з Ь₃ с₃

а[ b[ с[ а. Ьо с₂

а₃ Ь с_л

причем составляющие этого тензора

«1 h Су	> υι	«1 ^1 С1
(12 ^2 C1j		#2 ^2 ^*2
а3 с3		^3 ^3 С3

Введем более удобную для общих заключений систему записи элементов О. при помощи двойных индексов с таким расчетом, чтобы первый индекс при букве указывал порядок горизонтали, а второй—порядок вертикали. При такой записи мы обойдемся очевидно только одной буквой, и равенство (4) принимает вид:

«и а_п а,₃

й₂[ «₂₂ U₂₃ ⁼ ®π^α22®33 ~ ®11^α32^α23 "Ь ^а21®32^а13^—

а₃₁ а₃₂ а₃₃ — а₂₁а₁₂а₃₃ а₃₁а₁₂а₂₃ — а₃₁а₂₂а₁₃

или, переставляя в правой части тождества множители так, чтобы первые индексы следовали в натуральном порядке, имеем:

«11	«12	«13
»21	«22	«23
«31	«32	»33

— «11«22«33 ^— «11«23«32 +

+ ^α13 ^а21^а32 ^12^21^33 "Ь ^12^23^31 ^13 «22«31· (о)

В правой части тождества (5) каждое слагаемое имеет вид: ± α_1ιχα._2βα._Λγ, где а, β, у представляют любую перестановку натуральных чисел 1,2,3; знак + берется в том случае, если числа α, β, у образуют четное число инверсий (смотрите), знак — в противоположном случае. Очевидно число членов О. 3-го порядка будет 3!.

Возьмем и² количеств, расположенных в виде квадратной таблицы:

«11 »12 «13 ·	• · «1»
#21 &22 ^23 *	·· «2n	(6)
аШ ®й2 ^пЗ*	• · «mt
Составим произведение	из η	множителей,
взятых по одному из каждой		горизонтали
нашей таблицы:
αΐαια2α2«3α3 · ·	a">»	(V)
вторые индексы alt a2,.	an представляют

нек-рую перестановку из чисел 1,2,3.п.

Условимся брать произведение (7) со знаком (—1)“, где к—число инверсий в перестановке а, а₂. а„. Алгебранч. сумму слагаемых вида

Ы)^ка_1аа₂^.а_п,_я, (7)

распространенную на всевозможные перестановки а, а₂.а„ из л элементов 1,2,3,.,«, называют О. «-го порядка и записывают так:

«11 «12 ·	• «ln
«21 «22 ·	• «2η
а„1«„2.	• &ηη

= 2(-¹/«ι_αια_2β2α_3α3.α_ηαη.(8)

О. и-го порядка имеет « горизонталей и « вертикалей; и² количеств а,·,·, записанных схематически в левой части тождества (8), называются элементами О., а слагаемые правой части — членами О. Очевидно О. п-го порядка имеет «! членов. Правая часть тождества (8) дает краткую запись разложения О. «-го порядка. Таблицу (С), состоящую из « горизонталей и « вертикалей, называют матрицей квадратной в том смысле, что она порождает О. «-го порядка; числа α,-j· называются элементами матрицы. Мат-трица м. б. и не квадратной, а состоять из

mn чисел:

«11	а12 ·	* «ln
«21	«22 · 1	• · «2 η
«mi	«m2 ·	• · «mn

пусть например « > ш, тогда из матрицы (С) можно образовать О. наибольшего порядка т. Очевидно таких О. можно составить числом С"‘. Может случиться, что все О. порядков т-го, (m-l)-ro, (m — 2)-го, .,(р + 1)-го равны нулю, но из О. р-го порядка по крайней мере один не равен нулю. В таком случае,следуя Кронекеру.говорят, что матрица (6) имеет так называемый ранг р или характеристику р.

*4

Приведем нек-рые элементарные свойства О.: 1) О. не изменяет своей величины, если превратить горизонтали в соответствующие вертикали, и наоборот; 2) О. сохраняет абсолютную величину, но изменяет знак, если в нем переставить два параллельных ряда(то есть две горизонтали или две вертикали); 3) О. равен нулю, если два его параллельных ряда равны между собою; 4) если все элементы одного ряда О. умножить на число к, то и О. помножится на это число к; 5) О. не изменяет своей величины, если ко всем элементам какого-либо ряда прибавить соответствующие элементы параллельного ряда, умноженные на произвольное число ί; б) если элементы двух параллельных рядов О. соответственно пропорциональны, то О. равен нулю. На основе этих свойств обычно производят преобразования и вычисления О. Теорема сложения О.:

«11	«12 ·	• · «tn
«21	«22 ·	• · «2ll
«й + к и «/г	+ к	ain+kin
«Я1	«112·	• * апп

	«и	«12 · ·	«111		«11	«12 · ·	«111
	«21	(Х2О * *	«2 В		«21	«22 · ·	а2н
	(Хц	Λ/2 · ·	0>1,х		*<1	/С/2 · ·	kin
	anl	(Хп2. ·	«1111		«111	«112 · ·	апк

(9)

Теорема умножения О. (Бнне-Коши):

«11	«12 ·		ί.ι	bj2.	• ь1п
а 21	0 22 ·	• «2п	^21	b22.	• ^2п
«1.1	«,2 ·	• п	bп 1	Ь„2.	• · fr«n

С 1	«12 ·	«In
«21	«22 ·	* ^2 η
«111	to	• ^пп

(Ю)

где Cij равняется или 1) a_ub_lj + a_2ib_2j +. + a_nib_nj(комбинирование вертикалей множимого с вертикалями множителя), или 2) а_аЬ_п + ацЬу_г +. + a,_nb_jn

(горизонтали с горизонталями),

ИЛИ 3) Ciiibji + Oiibji +. -г ^ani^jn

(вертикали с горизонталями), или 4) я_ilb_lj + ацЬ₂у +. + a_inb_nj(горизонтали с вертикалями); например по 3) имеем:

«11«21		1и.Ьц		αΐ1^11+α21^12 ^11^21 ^21^22
α2ια22! по (4) ж		ЬцЬц e:		Cl12,Jll~t~a22,J12 ai2^21~ha22J22
«il«12		ЬцЬц		&13рИ ~b#12^21 ^11^12 ~Ь®12^22
«2l«22		Ь21Ьц		$2] ^ ]l~ ~ ^22^21 ^21 ^12^22^22

Легко проверить, что оба произведения равны друг другу.

Если в О. и-го порядка вычеркнем т горизонталей и столько же вертикалей и сдвинем остальные ряды, не изменят! их расположения, то получим новый О. М (п-т)-го порядка, называемый минором данного. С другой стороны, из вычеркнутых горизонталей и вертикалей образуется О. М т-го порядка, к-рый называется дополнением минора М. Очевидно и наоборот: М яв ляется дополнением минора M’. Например

«п я₁₂ а₁₃ а_и я₁₅

Я₂1 я₂₂ я₂₂ «₂₄ я₂₅

«31 я₃₂ я₃₃ я₃₁ я₃₅

Я41 Я,ц Ям а.

Я 1з я₄₄ «.,< Я-,Ί я₅₄ я,.

(Н)

«11	«12	«11
«41	«42	«44
«51	«52	«54

‘51 “52 “53 «54 “65

вычеркнем в О. 5-го порядка вторую и третью горизонтали и третью и пятую вертикали; тогда оставшиеся элементы дают О. 3-го порядка—минор

(12)

для О. (11), а на пересечении вычеркнутых рядов получается О. 2-го порядка—дополнение минора (12):

я₂₈ я₂₅ !

я₃₃ Я₃₆ t ⁽ ^

Очевидно и обратно: О. (12) является дополнением минора (13). Если дополнение минора М взять со знаком (—1)^{Σ + δ}, где Σ—сумма порядков вычеркнутых горизонталей, а S—сумма порядка вычеркнутых вертикалей, то получим так называемое алгебраическое дополнение минора М. В нашем примере минор (12) имеет алгеб-раич. дополнением

243 + 3*5 я₂₃ Я₂₅ ¹

«33 «85

Элементы О. сами м. б. рассматриваемы как миноры 1-го порядка. Для получения алгебраического дополнения элемента а,у надо вычеркнуть г-ю горизонталь и j-ю вертикаль, из оставшихся рядов образовать минор и взять его со знаком (—1)··. Если обозначим через А,у алгебраич. дополнение элемента а,у, то суммы

«Ч ji + ^a,2^1j₂ + π

^aiiA j + OllAij +.

равны значению О., если г=j, и равны нулю. если г Ф j (Безу).

Например:

“Ь «т -f- Q_niA„j

Chi 0>

<Χοι С1о.

13

а

^а23

^азз

^{! а}11^11 “Ь ^Д12^12 + ^αΐ3^13ϊ

ГГТР А Г-η ^{lT1 u}22 ^23 Л _ 1 ^{1+2 a}2t^fl23

где л_п-(. 1) „„ > ^n-1-i) _{а а}

, ¹⁺¹ ^22 ^2: ^32 ^а33 1+3

Ап=(—1) * ° J д²¹ “²²

I “31 “32

в этом случае говорят, что О. разложен по элементам горизонтали (первой). Еще пример: разлагая по элементам первой вертикали, легко проверить тождество:

«0	«1	С12	• · «и-1	«
-1	X	0	0	0
0	-1	X	0	0
0	0	0	X	0
0	0	0	-1	X
+ apr"		-ч-	«2жп“2	+

Укажем некоторые приложения О. п-го порядка. Обратимся к системе п линейных ур-ий с и неизвестными, решение и исследование которой в сущности и послужило при-

чиной возникновения теории О. Имеем: ΟχχΧχ + +··· + «ι„®„ ~ Ь_к

«2 _χΧχ + «гз^з + · · · + «зn^n ~

«»i®i -Ь Яца^а г · * 4" «nn«V — Определитель

	«11	«12 ·	а
ζ>=	«21	«22 ·	а
	«111	«и2 ·	а

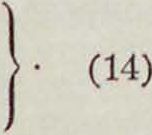
называется О. системы ур-ий (14). Умножая первое уравнение системы на алгебраич. дополнение А_хк элемента а_1к, второе—на алге-бранч. дополнение А_2к элемента а_гк и т. д., наконец последнее на алгебраич. дополнение А_пк элемента а_пк и складывая почленно результаты, находим:

Вх_к= В_к, (14)

где D_k—О., получаемый из В через замену в нем элементов к-й вертикали вторыми частями ур-ий.Полагая в ур-ии (14) fc=1,2,., я и считая ВфО, получаем решение системы:

x -°А

^xi _D >

D 2 _ Р«

I) > · · · ’ D

Отличие от нуля О. В является необходимым и достаточным условием, чтобы система я линейных ур-ий с я неизвестными имела единственное решение. Полагая в системе (14) b!=&,= .=6_П=0, получаем систему однородных линейных ур-ий. В этом случае ур-не (14) обратится в

Dx_k=О,

откуда видно, что обращение О. В в нуль есть необходимое условие существования решения. среди которого не все значения неизвестных равняются нулю. Приложения в геометрии: ур-ие плоскости, проходящей че-пез три данные точки (ж_х, у_и г,), (.гт₂, г/₂. г-₂), С?з. Уз< *з):

х у г 1 ^Хх у_к г_х 1 х₂ у_г г₂ 1 ^хз Уз i

= 0.

Ур-не кривой второго порядка, проходящей через пять данных точек (ау, у_к), (т₂, у₂),. ., (.т₅, ?/₆), Еыражается О. 5-го порядка: х^г х у у“ х у 1 ^χϊ ^χι Ух У хi Ух 1 _ о

^х1 Уз У Уз i

Объем тетраэдра в ф-ии координат его вершин равен

Χχ 2/, z_k 1

^{1 х}г Уз г₂ 1 ^{6 т}з Уз -3 1 х_л у t έ₄ 1

Определители широко применяются в теории линейных и квадратичных форм.

Большую роль в теории О. играет так паз. теорема Лапласа: О. я-го порядка равен сумме произведений из всех различных миноров, заключающихся в те горизонталях или вертикалях (т^п), на алгебраические дополнения этих миноров (мы не приводим этой теоремы в другой обобщенной редакции Коши). Имеется аналогия между теоремой Безу и теоремой Лапласа: если разложение по первой теореме сводит вычисление О. я-го порядка к вычислению я О. (я —1)-го порядка, то разложение по теореме Лапласа значительно понижает порядок О., но зато увеличивает число их. Так например, вычисление О. 5-го порядка по теореме Безу сводится к вычислению пяти О. 4-го порядка, между тем как по теореме Лапласа вычисление того же О. может быть сведено к вычислению десяти О. 2-го порядка и стольких же О. 3-го порядка.

Рассмотрим нек-рые специальные О. Пусть

	«11	«12 ·	• «1 η
В =	ft 21	«22 ·	• «2ιι
	«nl	«112 ·	• «ни

Заменим элементы этого О. алгебраич. дополнениями их:

	Δχχ	Αχζ	·· A- in
Δ =	А 21	Α22.	·· Агп
	nl	Α η 2	Λ * ·*ιηη

D и Δ называются в з а и м н ы м и (rezip-roke Determinante). Умножая В на 3, получаем:

	В 0 0.	0
D ·Δ =	ODO.	0
	0 0 0.	D

откуда

Δ =Dⁿ~¹ (ВФ 0).

Легко показать, что при D=0 и Δ=0. Если в О. В a_tj=dji, то такой О. называется симметрически м. Например

«11	«12	«13
«12	«22	«23
«13	«23	«33

О., взаимный данного симметрического, сам симметрический. Если а,у=— а μ и следовательно а,(=0, то О. называв гея. косым с и м м е т р и ч е с к и м, или а н т и с и м-метрически м. Например

0	«12	«13
— «12	0	«23
-«13	— «23	0

Легко проверить, что косой симметрический О. нечетного порядка равен нулю. В тензорном исчислении пользуются аналогичными терминами—симметрии, и антисимметрии, тензоров. Пользуясь теоремой сложения О., можно любой тензор разложить на два тензора— симметрический и антисймметричес-кий. В приложениях встречаютсяенмм трич. О., вычисление которых сводится к вычислению т. н. циклич. О. Симметрии. О. вида

	«1	Cf2*	•
		«3·	• «!
	«»	«1·	• «H-l

называется цикл и ч е с к и м О., или циркулянтом. Обозначая корень я-й степени из единицы через

2πΐ

со= е ^п,

имеем:

^аХ «2···«ιι (п-1)(п-2) П-1

°_г а₃.а_{к =(}_₁₎ а П (а_х +

«» «1 — «П-1

+ а₂со“ -у а₃о)Ф +. -) α,ω”-»*).

Определитель

	*п	*12 ·	•*1,1
D =	*21	#22 ’	• *2,1
	*П-1	*п—2*	·*„»

η к-рсш сумма квадратов элементов в каждой горизонтали равна единице, а сумма произведений соответственных элементов двух каких-либо горизонталей равна нулю, то есть в к-ром

a “i + * Ь -f-. + я “η=1,

α_ηα_μ -{- «,·₂«^₂ + · · · + Of{n^ajn ~ 6 (i j),

называется ортогопальным.Например при повороте прямоугольных координатных осей вокруг начала координат ф-лами преобразования будут ж,=а_гх + Ь_лу + с₂г,

Ух=*»ж + b₂у + c₂z,

«i=я₃.т + Ь_гу +с₃г,

где а,·, b_{ и с,· (г=1, 2, 3) — направляющие косинусы. О. этой системы

«i Ь₁ с_ая₂ Ь₃ с₂Я₂ Ь₃ с₃

будет ортогональным, потому что, как известно, будут существовать соотношения:

«ι+7l+Ci=1, o|-f bj+ei=1, ef+bl+Сз=1,

я !Я₂ + bjbj + с₃с₂ ⁼ 0, Я)Я₃ + Ь_кЬ з + с^з=О, я₂я₃ + Ь₂Ь₃ + с₂с₃=0.

Если в ортогональном О. переставить вертикали и горизонтали, то преобразованный О. опять будет ортогональным. Произведение двух ортогональных О. является также ортогональным О. Возведя ортогональный О. D в квадрат, получим 7>²=1, откуда Н=±1, то есть числовое значение всякого ортогонального О. равно единице (Якоби).

Рассмотрим т. и. функциональные О., в которых элементами являются ф-ии одного или нескольких переменных. Если элементы О. D являются независимыми переменными, то из тождества

D=я,·! A {i -j- a_i2A,·₂ “Ь. -Ь я_г,₍А

следует

OD

д<Чк

^А)к-

Если же элементы О. D являются ф-иями х, то с1Г) _ dD da,к _ ·νΐ. da/it

dx φβ oatk dx ~ ·“ ^,k dx ’ ik th

^dnn i V /t dn_i2, V и ^da<”

_dx + 2u^Aii_dx + --- + 2j^Ain _dx, i j

обозначая через a_ik, имеем при n=3:

#1 j Cf ,2 #J3		*11 *12 *13		#11 #12 #13
#21 #22 #23	+	*21 *22 *23	+	#21 #22 #23
#31 #32 #33		*31 *32 *33		#3l #32 #33

или

<7*11	do. 12 do, 12			#11	«12	«13
#21	*22	*23	+	^#21	<7 *22	<7*23
#31	*32	*33		#31	«32	«33
		«11	"^12	#13
	+	«21	«22	#23
		d #31 ^#32		,^#зз

Вычислим т. наз. степенной О., или определитель Вандермонда:

1	1.	,. 1
*1	ж2.	*
	ж|.	·®«
	1 ж”-1.	*Ln

О. I является целой однородной функцией

--ой степени переменных х_и х₂, х_п.

Так как замена переменного х_а переменным Χβ(α, β=1,2, .,η; αψβ) обращает О. V в нуль, то делителем О. V будет произведение Π(χ_α — Χβ), распространенное на всевозможные значения для а и β, причем будем считать а> β. Число множителей вида х_а — Χβ будет С я, то есть степень делителя будет та же, что и у ф-ии V. Следовательно возможно следующее равенство:

V=АН (Ха ~Χβ),

где А—численпый множитель. Из сравнения какого-либо члена О. F с таким же членом делителя следует, что А=1. Итак:

	1 1.	1
	Χχ χ2. χί £-5.	χ„ ί,·2	= 11(а5а-Жд), (15) α,/s p
	X?-1 xf1	грП-1 *
где α, /S=1,2,.		η И	а > β. Если в О. (15)

Χγ, х. ж„—корни ур-ия /(х)=0, то квад рат О. V называется дискриминантом (смотрите) ур-ия. Имеем:

V² =

1	1.	1
Χι	ж2.	ж„
ж?	ж!.	• - Ж»
ж”-	ж;·-1	.J.w

= ΐ(χ_α-χ_β)².

^α,β

Дискриминант есть симметрии, ф-ия корней ур-ия и поэтому м. б. В1>фажен рационально через коэфициеты ур-ия /(ж)=0. Обращение дискриминанта в нуль является необходимым и достаточным условием существования кратных корней ур-ия. Возвышая V в квадрат по правилу перемножения О. и введя Zi + ** + .-f ж?,=5_ьполучаем выражение для дискриминанта:

V² =

So

S.

S.

s*

.s_n_

.S_n

Si,— i S„ S_n ,.S_2n_₂

в к-ром суммы одинаковых степеней корней вычисляются по известным ф-лам Ньютона. Определитель

/l fi

f fi

η η

W(M_t, .,/*)=

fin-ΐψη-ν

1η

Γη

η

(1G)

/2

в к-ром f, /₂,., /„—ф-ии переменного а:, называется определителем Вронского. Взяв dW

, мы увидим, что изменится только порядок производных в последней горизонтали — повысится на единицу. Приведем еще такое свойство определителя Вронского: ИФЛ, А/, А/,)=А” - W(f_u U.fn), (IV)

где λ — нек-рая ф-ия х. -Равенство (17) напоминает известное свойство однородных ф-ий. Если менаду ф-иями /_lt /₂,/„ существует линейная зависимость, то определитель Вронского W(f_v /₂,. /„)=0; если же, наоборот, W(/i, /_а, .,/„)=0, то еще нельзя утверждать о существовании линейной зависимости: надо ввести добавочное условие—алгебраические дополнения элементов последней горизонтали О. не обращаются все в нуль в рассматриваемом интервале изменяемости аргумента. Определение линейной зависимости между ф-иями /!, / ,при помощи определителя Вронского требует существования производных этих ф-ий до (п—1)-го порядка, между тем линейная зависимость может существовать и тогда, когда функции этих производных не имеют. Необходимым и достаточным условием существования линейной зависимости между ф-иями /i,/₂,···,/» в интервале Ь является равенство ну лю О. G(f_u/„.,U) (Грам): ь ь

f h(x)f/x)dx Jи(х)(_г(х)ах. J f_l(x)f„(x)dx

а а а

Ь Ь b

fi(x)f/x;<tx Jft(pc)U(x)dx. J f₂(x)f„(x)dx

a a a

b b b

f fn(x)fi,x)dx J f_n(x)ft(x)dx. j 1„(x)f_n(x)dx

a a a

Пусть f₂, —ф-ииnнезависимых пе ременных x_tl х_г,х„ тогда О.

9/,	9/,	9/,
3*1	ϋΧ·2	9*„
9/з	9/а	9/2
ΟΧί	ОХ2	9oc„
9/л	9/n	9/„
ϋχι	дх2	9x„

называют ф у н к ц и о н а л ь н ы м определителем Якоби или якобианом и обозначают at/i/a. /_я) _

• а(“,*₂. х„)

Условие, необходимое и достаточное для того, чтобы п ф-ий от п аргументов были зависимы между собою, состоит в том, чтобы определитель Якоби, образованный для этих ф-нй, тождественно обращался в нуль. Если fu U, ···. in—функции у_и Уг,.·., Уп, ^а эти последние в свою очередь ф-ии£,:с₂, то

Hhh ··· At) _ Э(/)/2. fn) _ д(у,у₂. у_п) _ 9(*»*а ·· *n) a(i/,v_s. у_п) θ(*!*₂. х„)

Функциональный определитель Якоби играет важную роль при преобразовании кратных интегралов. Если η-кратный интеграл

f I ··* ff(^xu^xt,--,‘B_n)dx₁dx_t.dx„

преобразуется при помощи подстановки

^х( - <Р,<У1,У1.у_п) (г =1,2.п),

то

ff · · · 1(^χ1» ®*.X„)dx_t dx_t. dx_n =

.

где F(y_lt j/„ .,у_п)=/(?>!, φ,.<р„).

Определитель Якоби находит большое применение в теории интегрирования диферен-циальиых уравнений, особенно с частными производными.

Если

Ш-щ (^ΐ=1>².”)>

где F—однородная функция,то из определителя Якоби получается определитель Гессе:

o*f	d2F	a=F
dx’·	OxidXi	dXidXn
d*F	32F	a^F
dx-idxi		dx2dxn
d‘F	a*F	d*F
dxndxi	dxn0x2	дх&

Определителем Гессе пользуются в теории форм, а также при рассмотрении многих геометрия, вопросов, для решения которых приходится иметь дело с этими формами.

Понятие об О. в своем дальнейшем развитии получило обобщение—рассматриваются О. бесконечного порядка

^ап «12 «13 · · · «ι« · · · «21 «22 «23 · · · «2Л · · ·

«Л1 «л2 «ЛЗ · · · «ля· ·

(18)

при условии, что при неограниченном возрастании « выражение (18) стремится к определенному пределу, который и принимают за значение О. бесконечного порядка; для этих О. остаются справедливыми многие свойства конечных О. Кроме того вводят в рассмотрение О. высших измерений—кубические.

Лит.: Букреев Б. Я., Элемепты теории определителей, 2 изд., Киев, 1914; В а щ е и к 0-3 а х а р-ченко Μ. Е., Теория определителей и теория форм, Киев, 1877; К а г а п В. Ф., Основания теории определителей, Одесса, 1922; Нетто Е., Начала теории определителей, пер. с нем., Одесса, 1912; Ч е з а р о Э., Элемент, учебник алгебранч. анализа и исчислений бесконечно малых, ч. 1 и 2, Одесса, 1914; F i s с h e г Р. В., Ше Determinanten, В., 1921; N с t t о Е., Die Determinanten, 2 Aufl., В.—Ι,ρζ., 1925; Dos tor G., Elements de la theorie des determinants avec application 4 l’algebre, la trigonomftrie et la geometric analytique dans le plan et dans l’es-pace, 3 6d., P., 1905; Pascal E., Die Determinanten, Leipzig, 1900; Kronecker L., Vorlesungen iiber dic Theorie d. Determinanten, Lpz., 1909; J οροί) i C. G., tlber die Bildung u. die Eigenschaften d. Determinanten, Ostwalds Klassiker d. exakten Wis-senschaften, Lpz., 1896, 77; Hesse O., Die Determinanten, eleinentar bebandelt, 2 Aufl., Lpz., 1872; Kowalewski G., EinfOhrung in die Determinan-tentheorie, I-pz., 1925; Cesaro E., Corso di analisi algebraica, Milano, 1894. Д. Колянковский.