> Техника, страница 67 > Оптические приборы

Оптические приборы

Оптические приборы, приборы, В которых используются свойства света: отражение, преломление, диффракдия. интерференция, поляризация и т. д. В более узком смысле слова О. и. называются системы, состоящие из отражающих и преломляющих поверхностей и дающие изображения предметов, которые либо можно рассматривать глазом непосредственно либо можно принимать на экран. Эти системы обыкновенно входят как составные части в О. п. вообще. В дальнейшем рассматриваются О.

и. в более узком смысле слова. Почти все их свойства можно вывести на основании трех ниже приведенных законов: 1) закон прямолинейного распространения света в однородной среде; 2) закон отражение света (смотрите) и 3) закон преломления света.

Нее эти три закона м. б. объединены в один— принцип Фермд (смотрите Ферма принцип).

О. п. состоят, как обычно,из системы сред, ограниченных преломляющими и отражающими плоскими и сферическими поверхностями. Реже встречаются более сложные поверхности (наир. параболой !, вращения, цилиндр вращения и т. д.). В практике наиболее часты системы, центры сферич. поверхностей которых или лежат на одной прямой линии, называемой осью системы, или м. б. рассматриваемы как лежащие на одной прямой. Они называются оптическими центрированными система ми. Мы рассмотрим их свойства, изучение которых составляет предмет геометрия, оптики (смотрите Свет) и которые являются основаниями теории оптич. инструментов. Пространство, в котором находятся лучи, попадающие в оп-тнч. систему, называют пространством предмета, а пространство, где расположены лучи по выходе из системы,—п р о-странством изображения. Оба пространства мыслятся неограниченными. Лучи, выходящие из какой-нибудь точки освещенного предмета, по прохождении через систему вообще располагаются т. обр., что точки их взаимного пересечения обыкновенно группируются в небольшом пространстве, образуя т. наз. изображение точ-к и; оно называется действительным, когда пересекаются лучи, или м н и м ы м, когда пересекаются их продолжения. Исключение представляет случай, когда лучи в пространстве изображения близки к параллельности. В этом случае мы говорим, что изображение лежит на бесконечности. Поверхность, которой касаются все лучи, образующие изображение точки, носит название каустической, или каустики. В случае идеального изображения точки все лучи собираются в одну точку (получается т. и. гомоцентрический пучок лучей).*

Основной задачей теории О. п. является исследование взаимного расположения лучей, вышедших из ряда светящихся точек (предмета) и прошедших через оптич. центрированную систему, а также и выяснение такого подбора и расположения элементов системы, при которых лучи, вышедшие из каждой освещенной точки предмета, по прохождении через систему дали бы изображение минимальных размеров, расположение же самых изображений было бы подобно расположению точек. Эта задача вообще чрезвычайно сложна и на практике почти всегда решается с известным приближением, зависящим в большинстве случаев от величины сферических поверхностей по отношению к их радиусу кривизны. Наиболее просто решается эта задача, когда отношения поперечников сферич. поверхностей к их радиусам кривизны, а также углы лучей с осью системы настолько малы, что их квадратами и высшими степенями можно пренебречь.

* Такое идеальное изображение в действительности невозможно, т. к. даже в том случае, когда по законам геометрич. оптики все лучи должны были <5ы пересечься в одной точке, изображение будет иметь конечные размеры (порядка размеров световой лолны) благодаря волновой природе света.

Это т. наз. случай гауссовской оптн-к и. В этом случае из законов преломления (или из общих соображений о свойствах изображения) можно вывести ряд нижеперечисленных свойств и закономерностей. 1) Лучи от светящейся точки, по прохождении через систему, всегда дают изображение (действительное или мнимое) этой точки; прямолинейный, перпендикулярный оси предмет имеет всегда прямолинейное, перпендикулярное оси изображение. 2) Во всякой оптич. системе имеются две перпендикулярные оси плоскости—одна в пространстве предмета, другая в пространстве изображения, обладающие тем свойством, что любая точка на одной плоскости имеет свое изображение на другой плоскости на том же расстоянии и по ту же сторону от оси. Эти плоскости называются главными плоскостями, а их пересечения с осью называются главными точками системы.

3) Пучок лучей, параллельный оси, по прохождении через систему собирается в некоторую точку на оси. Имеются две такие точки, соответственно прохождению лучей в двух противоположных направлениях. Эти точки называются главными фокусами системы. Плоскость, перпендикулярная оси системы и проходящая через главный фокус системы, называется главной фокальной плоскостью. Впей лежат все изображепия, даваемые параллельными пучками, идущими наклонно к оси. 4) Имеются две точки с таким свойством, что всякий луч, входящий в систему через одну из этих точек под заданным углом к оси, выходит через другую под тем же углом. Эти точки называются узловыми точками системы. Главные и узловые точки и главные фокусы называются кардинальными точками системы; их положение определяется элементами системы (радиусами кривизны) поверхностей, показателями преломления сред, через которые проходит свет, и расстояниями между поверхностями. В том случае когда показатель преломления среды с обеих сторон системы одинаковый, узловые точки совпадают с главными.

Если мы обозначим через х расстояние предмета от обращенного к нему главного фокуса системы, через х_г—расстояние изображения от другого главного фокуса, через F и F_l—расстояния главных фокусов от лежащих в их пространстве главных точек, через у и у₁ — величины предмета и его изображения, через в—угол с осью, составленный каким-нибудь лучом, идущим из осевой точки предмета, и через —угол с осью того же луча, когда он проходит через осевую точку изображения, через п и η_ί— показатели преломления в пространстве предмета и изображения, то получим такие зависимости:

хХх — FF j, (1)

пуи^щур^. (3)

Первая формула носит название ф-лы Ньютона, третья—ф-лы Лагранжа-Гельмгольтца. Эти соотношения определяю, собой место и ве личину изображения. Величины F и Fi называются главными фокусными расстояниями системы. Из ф-лы следует, что для случая η=rij получается

F=-Fi. Величина ^v- называется линейным увеличением системы, величина называется угловым увеличением. Положение светящейся точки и ее изображения входят в формулу (1) одинаковым образом; такие точки называются с о-пряженными. Если расстояние предмета от его главной плоскости обозначим через d, а расстояние изображения через /, то для случая одной преломляющей поверхности обе главные точки совпадают с вершиной поверхности и из ф-лы (1) и закона преломления получается следующая ф-ла:

П n_t _ n-Tli

d г ’

где г—радиус кривизны поверхности. Для случая бесконечно тонкой линзы с радиусами г и г i получаем это общая формула для всех видов тонких линз. Во всех этих формулах расстояния считаются положительными, если они отсчитываются от фокальных или главных плоскостей но направлению движения света, и отрицательными в противоположном случае: радиусы сфер, отсчитываемые от поверхности к центру, положительны, если они совпадают с направлением движения света. Величина предмета у и изображения у i считаются положительными по одну сторону оси и отрицательными по другую.

Основные типы л и н з и положения в них главных точек HH видны на фигуре 1,

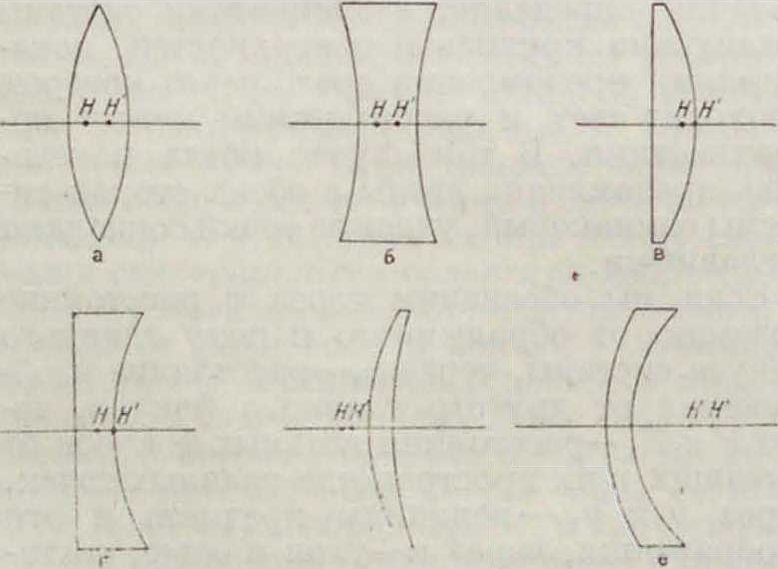
Фигура 1.

где: а—двояковыпуклая линза, б—двояковогнутая, в—плосковыпуклая, г—плоско-вогнутая, д—положительный мениск, е— отрицательный мениск. Употребление кардинальных точек дает возможность находить место и величину изображения при помощи построения.

Все вышеприведенные выражения справедливы для лучей одинаковой длины волны, монохроматических (смотрите Монохроматиче-ский свет), то есть в предположении, что для данной среды все лучи имеют одинаковый показатель преломления. Если же точка ис пускает лучи различной длины волны, то каждая среда будет иметй для различных лучей разные показатели преломления и следовательно разные места изображений. Это явление носит название хроматической аберрации. Благодаря ей получается нерезкость краев изображения у неодноцветных предметов. Система, в которой совпадают фокусы лучей двух каких-либо цветов, носит наименование а х р о м атнче-с к о и (смотрите Ахроматическая система стекол). Вообще говоря, при совпадении фокусов лучей двух цветов, фокусы лучей других цветов не совпадают: получается т. н. в т о-ричный спектр, тоже дающий нек-рую окраску изображения, хотя и очень слабую. Системы с сильно уменьшенным вторичным спектром называются апохроматами. Случай гауссовской оптики является идеальным. Он дает возможность изучить ход лучей, близких к оси системы. Следующее приближение к действительным системам мы получим, если предположим, что пятые степени отношения диаметров действующей части сферич. поверхностей к их радиусам кривизны и углов лучей с осью исчезающе малы. В этом случае анализ изображений, получаемых с помощью оптических систем, дает возможность разложить недостатки изображения на следующие составляющие, получившие общее название аберраций (отклонений).

Предположим сначала, что через систему проходят лучи монохроматические. Разобьем первую поверхность системы концен-трич. кругами, коаксиальными оси системы, на ряд узких зон. Если светящаяся точка лежит на оси системы, то каждая зона дает на оси изображение точки, но вообще говоря, эти изображения не будут совпадать друг с другом. Получается т. н. сферическая аберрация на оси. Расстояние изображения, даваемого заданной зоной от изображения, полученного от центральной зоны, отсчитываемое по оси, называется п р о-дольной сферической аберраци-е й. Вследствие сферич. аберрации сечение пучка лучей, сходящихся по прохождении через систему, плоскостью, перпендикулярной оси (изображение точки на экране), всегда представляется в виде нек-рого кружка, т. н. к р у яг к а рассеивания, к-рый в определенном месте оси имеет наименьшие размеры. Если светящаяся точка леягит не на оси системы, то ее изображения, даваемые различными зонами на экране, перпендикулярном оси, будут рядом колечек, диаметры которых изменяются от зоны к зоне и центры которых будут леясать на прямой, проходящей через ось системы. Совокупность этих изо-браягений дает кометоподобное пятнышко. Этот недостаток носит название к омы. В тех случаях, когда изобраягение точки лежит недалеко от оси, существует одно условие, при к-ром кома исчезает и все лучи собираются в одну точку, если система свободна от сферич. аберрации на оси. Это условие носит название условия синусов и выражается так: произведение из синуса угла, образованного лучом, выходящим из точки на оси с этой осью, на показатель преломления в среде предмета, равно произве дению синуса угла, образованного тем же лучом в пространстве изображения, на показатель преломления среды изображения. Точки на оси системы, для которых отсутствует сферическая аберрация на оси и соблюдается условие синусов, носят название а п л а-натических точек.

Кома, вообще говоря, сопровождается астигматизмом (смотрите). Дело в том, что даже очень узкий пучок лучей, проходящий через оптич. систему под большим углом к оси, не

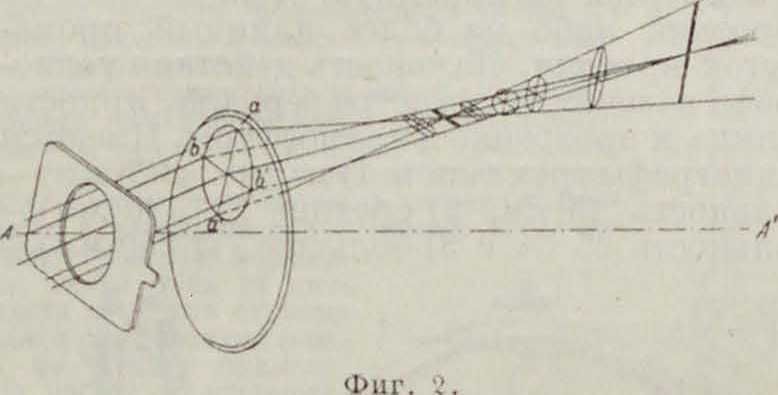
сходится в одну точку, а имеет два наибольших сужения в виде двух взаимно перпендикулярных линий, находящихся на нек-ром расстоянии друг от друга. Это строение пучка представлено на фигуре 2 (АА₁—оптич. ось). При передвижении экрана вдоль оси мы будем иметь два места, где изображение точки представляется в виде короткой линии. Если из пучка лучей выделим две пары: одну аа, лежащую в плоскости, содержащей ось системы (т. н. меридиональные лучи), и другую ЬЬ, в плоскости, перпендикулярной первой (сагиттальные), то два места наибольших сужений совпадут с фокусами этих пар лучей. Если мы будем рассматривать совокупность изображений точек, расположенных в плоскости, перпендикулярной оси системы, то все изображения, даваемые меридиональными и сагиттальными лучами в отдельности, будут лежать соответственно на двух кривых поверхностях. При отсутствии астигматизма у системы эти две поверхности сливаются в одну, которая в общем случае тоже будет кривой. Существует общее простое условие, при к-ром эта

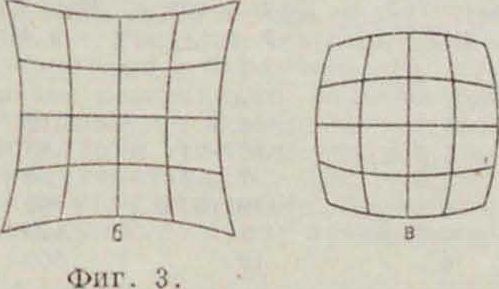
поверхность до нек-рого расстояния от оси будет практически плоской, это т.н. условие Петцваля.

Идеальное изображение должен быть вполне подобным предмету. Нарушение этого подобия (т. наз. о р т о с к о η п и) носит название д и с т о р с и и. Вследствие дисторсии изображение прямолинейного предмета на экране будет иметь искривленные линии. Два вида искривления б, в изображения прямоугольной сетки а вследствие дисторсии показаны па фигура 3. Перечисленные выше пять родов аберраций: сферич. аберрация, кома,

♦

астигматизм, кривизна изображения и ди-сторсия называются пятью аберрациями Зейделя для монохроматического пучка лучей.

Если светящаяся точка испускает лучи различной длины волны, то возникают новые недостатки изображения, с к-рыми приходится бороться при конструировании ои-тич. системы. Помимо устранения хроматич. аберрации, упомянутой выше и представляющей наиболее значительную из всех аберраций, в нек-рых случаях принимается в расчет еще ряд недостатков. Из них мы назовем хроматич. разницу сферической аберрации, хроматич. разницу увеличения и вторичный спектр. Первая состоит в том, что при уничтожении сферич. аберрации для одного какого-нибудь цвета лучи другой длины волны, прошедшие через разные зоны системы, не сходятся в одну точку. Вторая же возникает от того, что величина изображения, образованного лучами различной длины волны, не одинакова. Нетрудно вывести формулы, по которым молено вычислить эти аберрации, если считать, что пятые степени углов лучей с осью и отношений отверстий линз к радиусам кривизны исчезающе маты. Это условие в действительных системах, и то не во всех, является только приближенным, а потому такими ф-лами можно пользоваться лишь для ориентировочных вычислений. Взаимное расположение лучей по прохождении через систему с большой степенью точности дает тригонометрия, просчет хода лучей через систему, на основании законов преломления и отражения. Этим способом обычно и пользуются в точных расчетах. Конечно, в случае многих поверхностей и нескольких лучей, эти вычисления требуют очень много времени и внимательности. Оптич. систем, вполне свободных от вышеуказанных недостатков, почти не существует. При конструировании обыкновенно стремятся ослабить наиболее существенные для данной системы недостатки, за счет увеличения менее существенных.

Весьма большое значение в оптич. системах имеет ограничение пучков лучей, проходящих через систему. Это ограничение делается с помощью плоских пластинок с круглыми отверстиями, называемых д и а-ф р а г м а м и; иногда в качестве диафрагмы служит оправа линз системы. Если мы в пространстве предмета построим изображения всех диафрагм системы, то изображение диафрагмы, к-рое из дайной точки предмета будет видимо под наименьшим углом, называется входным зрачком системы. Изображение входного зрачка в пространстве изображения называется выходным зрачком системы. Входной зрачок определяет собой количество лучей, проходящих через систему, и следовательно яркость изображения. Диафрагма, поставленная в плоскости какого-либо из действительных изображений, даваемых последовательно частями системы, резко ограничивает используемую часть изображения. Она определяет поле зрения системы. В этих же местах системы ставятся марки, перекрестки нитей, позволяющие привести наблюдаемую точку предмета в заданное место поля зрения. Кро-

ме того величина и место диафрагмы могут оказывать влияние на качество изображения и его подобие предмету.

Все указанные выше особенности оптич. систем учитываются при конструировании О. п. Последние можно разбить на несколько типов. 1) Телескопические системы, в которые входит и выходит параллельный пучок лучей. К ним относятся зрительные трубы всякого рода, прицельные приспособления и т.д. 2) Микроскопические и проекционные системы. В них попадают расходящиеся пучки лучей от точек близкого освещенного предмета и оттуда лучи выходят параллельные или почти параллельные. Сюда относятся микроскоп, лупа, проекционный объектив, коллиматоры и т. д. 3) Фотографические объективы. Они дают на конечном расстоянии уменьшенное изображение предмета, находящегося на большом расстоянии (превышающем в десятки раз их фокусное расстояние). Действие их обратно действию проекционных объективов. Среднее положение между 2 и 3 занимают т. н. репродукционные объективы и оборачивающие системы из линз. Указанные отдельные типы часто входят как составные части в более сложные приборы, наир, зрительная труба и коллиматор входят в спектральные приборы, зрительная труба и микроскоп—в дальномер и т. д.

Лит.: Хвольсон О., Курс физики, т. 2, Берлин, 1923; Г рим зе ль Э. Курс физики, ч. 3, М.— Л., 1926; Г а в а р р е Ж., Теория Гаусса, примененная к сферическим зеркалам и стеклам, Москва, 1891; К и с л о в Η. М., Теория оптических инструментов, И., 1915: С г а р 8 k 1 S. u. Eppenstein О., Grundziige d. Theorie d. optischen Instnimente nacli Abbe, 3 Aufl., Leipzig, 1924; G 1 e i c h e η A., Lehr-buch d. geometrischon Optik, Lpz., 1902; Rolir M. Die Theorie d. optischen Instrumento. B., 1904; itandb. d. Physik, hrsg. v. H. Geiger u. K. Scheel. B. 18, Geo-metrische Optik, B., 1927; D r u d e P., Lehrbuch d. Optik, 3 Aufl., Lpz., 1912; Handbuch d. Experimental-physik. hrsg. v. W. Wien u. F. Harms, B. 20, T. 2, Lpz., 1929. В. Линнии.