> Техника, страница 68 > Остойчивость судов

Остойчивость судов

Остойчивость судов. Остойчивостью называется способность судна возвращаться в первоначальное положение по прекращении действия силы (или пары сил), вызвавшей наклонение его.

1) Основные понятия. Судно, как и всякое тело, находится в покое, если действующие на него силы удовлетворяют условиям: ХР=0 и ХМ=0, то есть находятся в равновесии. Судно не будет опрокидываться, если внешняя сила или пара сил, вы

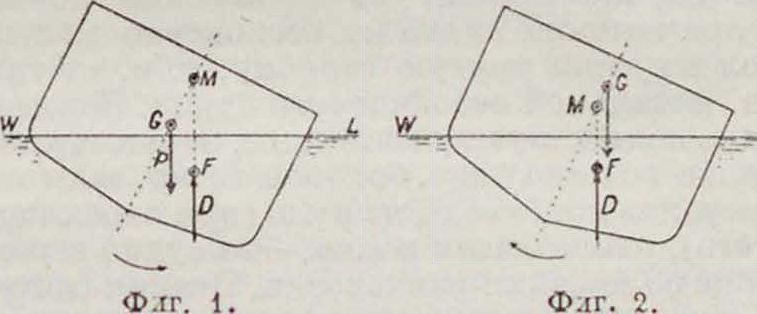
водящая его из состояния покоя (возмущающая сила, опрокидывающий момент), вызовут такую перегруппировку действовавших ранее сил, что образовавшийся от этого восстанавливающий момент будет достаточным для возвращения судна в исходное положение, по прекращении действия возмущающей силы или пары сил. Кроме того во избежание опрокидывания до прекращения действия возмущающей силы, опрокидывающий момент должен нарастать по мере наклонения судна медленнее, чем момент восстанавливающий, а при уменьшении последнего—убывать быстрее. При этих условиях судно может плавать в любом (до известного предела) наклонном положении, сохраняя в этом положении устойчивое равновесие (например на волне, при крене под парусами). На судно, наклоненное до нек-рого угла и затем предоставленное самому себе, действуют две силы: 1) сила тяжести Р (фигура 1), приложенная в ц. т. судна G, и 2) сила под-дерясапия Ώ, равная предыдущей, но направленная в противоположную сторону и прохолящая через ц. т. F объёма подводной части корабля (центр величины—ц. в.). Обе эти силы либо образуют пару сил с плечом h либо лежат на одной прямой и т. о. взаимно уравновешиваются; пара сил может стремиться вернуть судно в исходное положение (фигура 1) или будет опрокидывать его дальше (фигура 2). Оба эти случая определяются положением относительно центра тяжести точки пересечения М (метацентра) линии действия силы поддержания с диаметральной плоскостью судна: если М лежит выше G—судно остойчиво, если М лежит ниже

G — судно не остойчиво и если М совпадает с G — судно находится в состоянии безразличного равновесия. Для случая судна, стоящего в прямом положении на тихой воде (фигура 3), мы имеем дело только с двумя указанными силами, направленными по одной вертикали: силой поддержания и веса, и ур-ия равновесия сведутся к одному: ϊΖ=О,

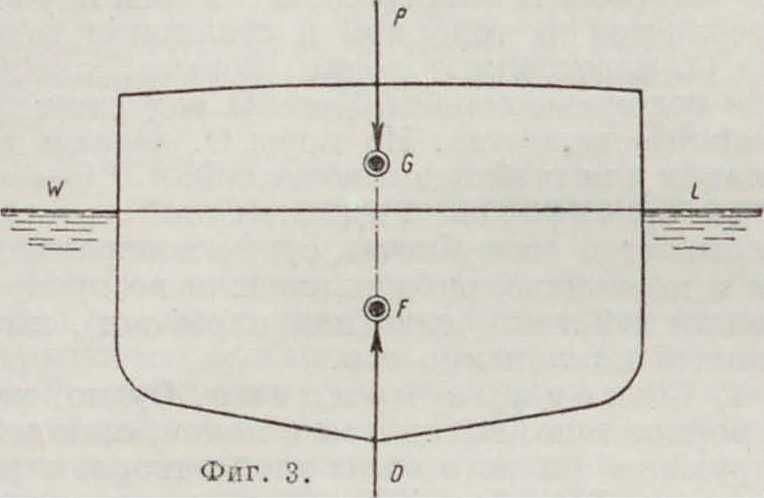
или, расшифровывая, D=Р—у равнение пловучести. Устойчивость судна в таком случае зависит от положения точки М при наклоне судна на бесконечно малый угол в ту или другую сторону, то есть от так называемым начальной остойчивости судна. Если на судно подействуют новые силы, например давление воды на винт, боковой ьетер.залп по борту, давление воды иа руль (при перекладке его), набегающая волна,—то судно выходит из положения равновесия. Всякая система сил, как известно, может быть представлена в виде одной силы, приложенной в любой точке (в нашем случае в центре тяжести судна), и пары сил; разлагая их по трем основным направлениям, получаем три силы, вызывающие поступательное движение судна [ход вперед или назад, дрейф (боковое перемещение),всплытие или погружение], и три пары сил, поворачивающих судно вокруг трех осей (крен, диферент и изменение курса). Для удобства исследуют действие каждой из составляющих отдельно; при этом направленные горизонтально силы и действующая в горизонтальной плоскости пара сил, как не изменяющие осадки и не наклоняющие судна, для изучения О. с. интереса не представляют. Наибольший интерес представляет пара сил, плоскость действия которой лежит перпендикулярно продольн. оси

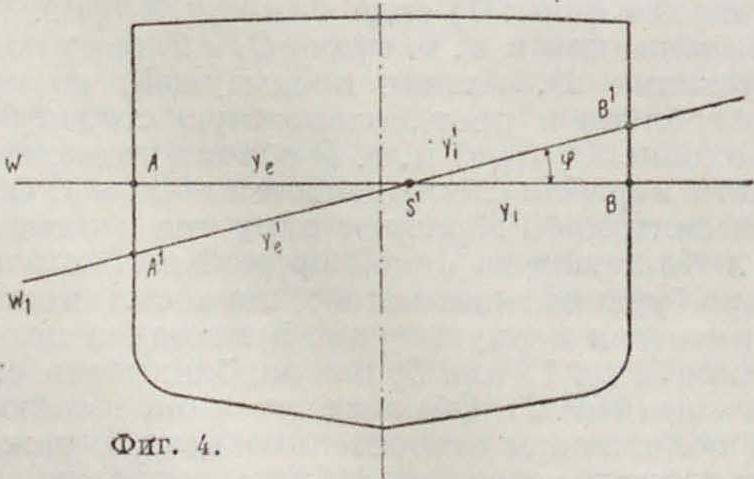
судна,—кренящая пара сил. Т. к. мы рассматриваем действие одной пары сил, то объём подводной части судна должен оста ваться неизменным при повороте его на любой угол. При наклонении частично погруженного тела на малый угол φ (фигура 4) новая ватерлиния АВ пересечет старую АВ в некоторой точке S; положение этой точки можем найти из условия равенства погрузившегося (ВВS) и вышедшего из воды (HHS) объёмов; называя у₍ и у_с ординаты погрузившейся и вынырнувшей части первоначальной ватерлинии, а у_{ и у_е соответственные ординаты новой ватерлинии от липни их взаимного пересечения, обозначая длину (то есть направление, перпендикулярное плоскости чертежа) через L, а диференциал длины через dx и полагая, что участки А А и BB—прямые линии, имеем L L

U у,у, Sin Ψ dx - l I y_eysin<pdx=0~

0 0 L

= I sin ψ j (y,y - y_ty_e) dx,

0

T. e. интеграл равен 0. При весьма малом угле наклонения у₍esу₍ и у_е=у_е, и т. о.

L

If (у)~Уг) dx=0.

о

Левая часть этого выражения представляет статич. момент площади ватерлинии относительно оси S; т. о. получаем, что обе смеишые ватерлинии, получающиеся при наклонении тела на очень малый угол, пере

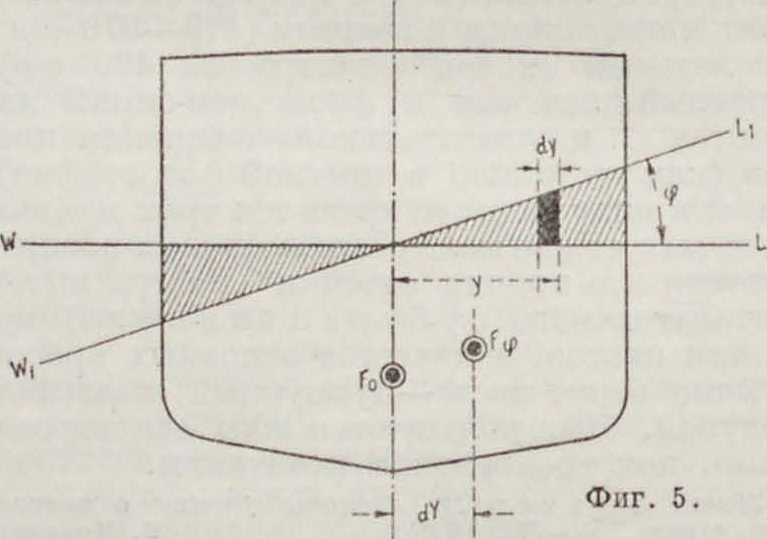
секаются в общем ц. т. площадей их. Во время поворота тела на конечный угол крена ряд последовательных ватерлиний опишут внутри тела нек-рую цнлиндрич. поверхность—подвижную аксоиду (неподвижной аксоидой является поверхность воды), причем каждая ватерлиния касается ее по прямой, параллельной длине судна и проходящей через ц. т. мгновенной ватерлинии. Изменение формы погруженного объёма при крене вызовет соответственное изменение положения ц. в., который перейдет из F₀в Fip. При наклонении плавающего тела (фигура 5) одна часть корпуса будет входить в воду, другая—выходить из нее (входящий и выходящий клин); перемещение ц. в., вызванное таким изменением формы погруженной части корпуса судна, м. б. определено из того условия, что момент массы для нового положения ц. в равен алгебраич. сумме моментов масс изменений объёма. Полагая, что оси×и Y являются главными осями инерции, получаем по общему свойству главных осей инерции

V dX=Jx dv=d<pj I’xy dx dy=· 0 VdY=Jy dv=dg>J Jу² dx dy=l_x dq> VdZ- Jgdv-ίd²<pff у^г dx dy - I_x d^l<p

(т. к. г=у d<p), где X, Y, Ζ и χ, у, ζ соответственно координаты ц. в и ц. т. диферен-циала объёма dv; пренебрегая dZ, как бесконечно малой высшего порядка малости сравнительно с dY, имеем

==0; dY=γ dip=ds,

где ds—бесконечно малая дуга перемещения ц. в.;замечая, что радиус кривизны всякой кривой ρ =, получаем

θφ=Τ ^{И α}Υ=ρ_φάφ.

ΰφ называется истинным метацентрич. радиусом для любого наклонного положения плавающего тела.

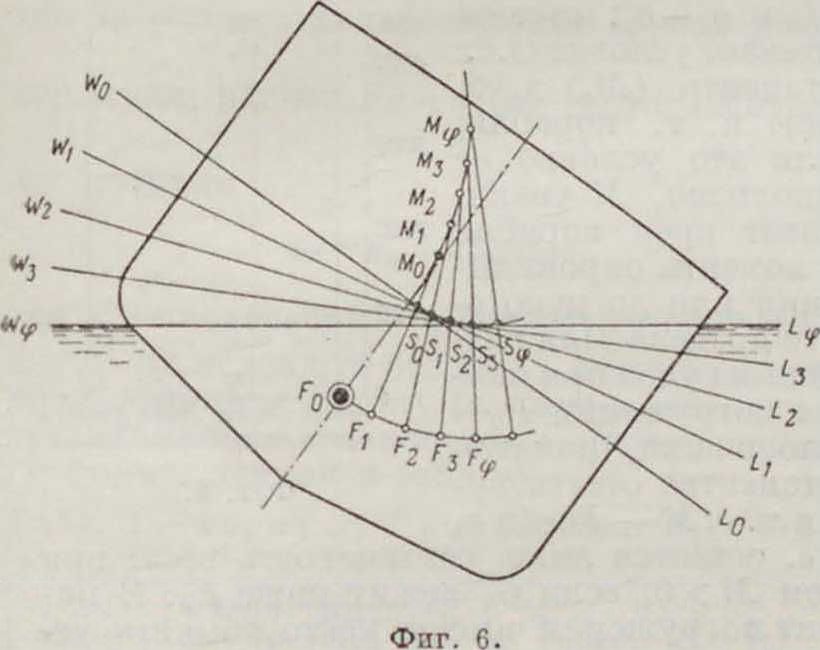
Т. о., резюмируя вышесказанное, получаем следующую картину физич. явлений при наклонении плавающего тела парой сил: последовательные ватерлинии обкатываются по некоторой цилиндрич. поверхностиSJSq, (фигура fi), касаясь ее всегда своим ц. т.; в то же время ц. в перемещается все время т. о., что касательная к кривой перемещения параллельна соответствующей ватерлинии и радиус кривизны в каждой точке равен истинному метацентрич. радиусу для того же угла крена. Зная положение ц. в при любом угле крена, мы легко определим положение метацентра и прочие эдементы О. с.

2) Начальная О. при крене. Пусть (фигура 7) корабль накренен опрокидывающим моментом M_R=R Ь па угол <р, грузовая ватерлиния его GWL перешла при этом из положения W в положение W_lt а ц. в из положения F₀ в положение F, зависящее как от угла крена, так и от формы корабля; при этом ц. т. останется на место (G₀), но направление сил тяжести и поддержания по отношению к кораблю изменится из показанного пунктиром в показанное сплошными линиями D и Р. Тогда величина восстанавливающего момента М получится из ур-ия M_R=M-Ph. Продолжая силу D до ее пересечения с диаметральной плоскостью кораб ля в точке М₀, называется метацентром, из фигура 7 получим, что плечо h равно

h=M₀G₀ sin φ.

Метацентрическая высота

MqGq ~ MqFq —jF;Go j

где M₀F₀—поперечный метацентрически и радиус ρ„, a F₀G₀—высота ц. т. над ц. в., равная а₀. Т. о. имеем:

М - Ρ(ρ₀ - а₀) sin φ, (1)

т. и. метацентрическую формулу остойчивости. Величина М определяет способность к выпрямлению данного корабля при данном угле наклонения. Из ур-ня (1), зная кренящий момент M_R=R-b, можно определить угол крена из ур-ия:

Сама величина Ρ(ρ₀ - а₀) характеризует абсолютно сопротивляемость наклонению различных кораблей в данном положении, а ρ₀ — α₀ относительную величипу этой сопротивляемости на т водоизмещения. Величина ρ₀ остается практически постоянной лишь для небольших углов крена (δ —10°), так как вообще ρ=f(<p) зависит от формы корпуса корабля; величина а„= Const при неизменном расположении весов корабля; поэтому формула (1) может применяться лишь для небольших углов наклонения и характеризует начальную остойчивость корабля. Изменение формы объёма подводной части корабля при крене состоит в переносе клина объёма V, заштрихованного на фигуре 7 пунктиром, в положение, заштрихованное сплошными линиями; при этом ц. т. этой призмы

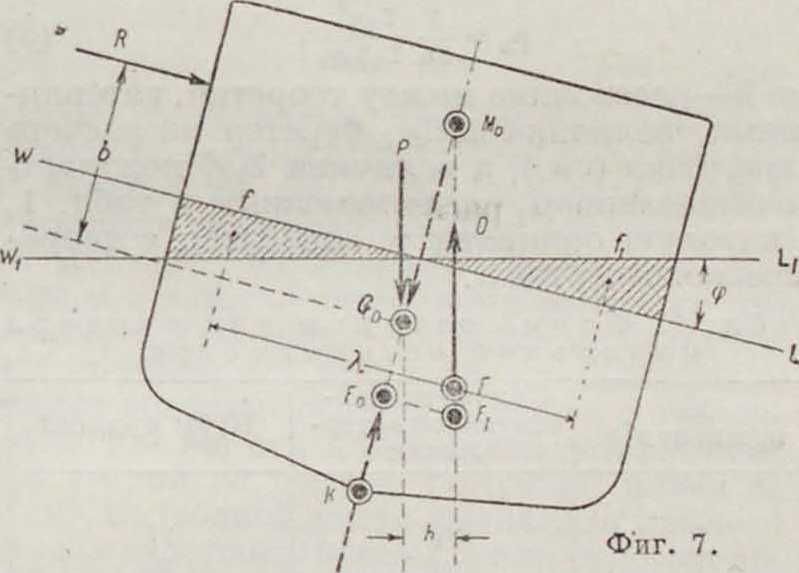
перемещается в h на расстояние А, ап. в F₀перемещается в направлении движения ц. т. призмы на величину δ=·* А. Если А—проекция перемещения ц. т. клина на плоскость первоначальной ватерлинии, то ρ„=_у ’’_{g φ}и формула (1) м. б. заменена

^M=D{v~ sin φ°о)^{sin Δ} (^ν · А - ^ν · “о sin φ)

(ф-ла Атвуда), где Δ=_у —плотность воды.

При малых углах наклонения заштрихованные на фигуре 7 тр-ки можно считать равными, и объём клина при бесконечно малом φ, или вертикальных бортах, по всей длине корабля L

ν=2 J y²sin<p dx, о где у—ордината грузовой ватерлинии, и интеграл берется по всей длине корабля L. Величина проекции перемещения ц. т. элемента клина λ м. б. принята при тех же условиях равной 2· у; тогда получаем,что проекция перемещения точки F₀ на направление параллельное GWL, т. e. F₀F, будет: L

* · £ I* V³ sin <pdx

ад -Цг- ->

где V—объём подводной части судна, а т. к. Со=F₀F : sin φ, то

| Г у³ dx

е₀=-%-- (2)

Обозначая числитель—момент инерции грузовой ватерлинии—через 1_Х и замечая, что

l_x=® j у³ dx. имеем ρ₀=1_X:V. Т. к. I_x=S r², о где S—площадь грузовой ватерлинии GWL, а г—радиус инерции ее, пропорциональной ширине корабля: г=кВ, то 7 в³

es₀ -чу

Приближенные значения величины к_х для различных типов кораблей можно найти в справочниках. Точная величина ρ„ получается вычислением табличным способом интеграла 1_Х по правилам приближенного интегрирования. Напр., пользуясь правилом трапеций, имеем

Go —

± Spvf 3h -0-0У1’

(3)

где h—расстояние между теоретич. ватерлиниями, величина Σ₀Σ₀ι/,· берется из расчета пловучести (смотрите), а величина Σ₀?/? получается вычислением, расположенным в таблице 1, в которую ординаты у заносятся с теоретического чертежа.

Таблица 1.—Ф о р м а таблицы для расчета начальной остойчивости.

№ шпангоутов	Ординаты действующей ватерлинии	Кубы ординат
0	Vo	υο
1	Vi	νϊ
г	У 2	уг
л-1	Уп-1	«i.
*	Уп	Уп
	Сумма 2 =
Поправка ‘ (i/3 + vj =
Исправленная сумма		s.«s-

При пользовании одним из правил Симпсона или Чебышева, как формула (3), так и форма табл. 1 изменяются. Величину а₀ определяют, зная G₀K (фигура 7), находимое из таблицы нагрузок, и F₀K, получаемое при расчете пловучести. Для данного корабля при неизменной нагрузке а₀=Const. Нек-рые численные значения ρ — а₀, характеризующие сравнительную сопротивляемость различных кораблей наклонению, даны ниже.

Тип судна е-а в м

Речные пароходы большие. 1,0—з,о

» » малые. о, 5—1,о·

Линейные корабли.. 0,9—1,8

Лилейные крейсеры.. 0,8—1,6

Крейсеры, эскадренные миноносцы. 0,7—1,0-

Парусные яхты малые.. 1,0—1,5

» » большие. 1,0—2,5

Парусные суда.. 0,6—0,9

Рыбачьи суда.. 0,7—о,8

Товаро-пассажирские пароходы. 0,3—0,7

Буксиры, ледоколы.. 0,5—0,6

Грузовые пароходы.. 0,3—0,6

Транса глантич. пароходы. 0,2—0,5

Сравнительное положение точек F₀, G₀ и М& для нек-рых судов дано на фигуре 8. Если ме-тацентрич. высота A/₀G₀, а вместе с ней и восстанавливающий момент М > 0, то судно· остойчиво; если М<0—судно не остойчиво; если М=0, судно в Знак М зависит от знака ρ₀ — α₀; отсюда вытекает условие О.с.: метацентр (М₀) должен быть выше ц. т. корабля.

Если это условие не выполнено, М увеличивает крен корабля до момента опрокидывания или до некоторого предела. Для подводных судов при полном погружении F₀— неподвижно, понятие метацентра отсутствует и т. о. М=—Ра sin φ, то есть остается лишь остойчивость веса; при этом М > 0, если G₀ лежит ниже F₀. В момент погружения имеют место обычные условия, осложняемые приемом жидкого груза при заполнении цистерн. Т. к. вообще в надводном положении G₀ лежит выше F₀, то при погружении точка F₀ должна пройти через G₀, и в этот момент лодка находится в положении неустойчивого равновесия. Это обстоятельство требует при конструировании подводных лодок тщательного изучения условий их остойчивости в момент погружения (смотрите Подводные суда).

Для приближенного вычисления ρ„ применима формула

В г _У2

^ρ° ~ 11, *Т t ’

где В и Т—ширина и углубление судна, у—коэфициент полноты площади грузовой ватерлинии и δ — коэфициент водоизмещения. Эта формула с достаточной степенью точности м. б. принята в следующем виде:

3) О. с. при больших углах крена. Ф-ла (1) остается и в этом случае в силе, но величина ρ переменна, определяясь формой корабля и углом φ, поэтому можно написать, что

Μ=Ρ(ρ_φ-α₀)δ ηφ. (4)

До входа кромки палубы в воду ρ^ρ,.

4000

3000

2000

1000

	»0	Me— So
	So
			Mo
			Mo
			Go Go*
_ί5.		Fs>	Й Fc.

Линейн Пасса“ Рыбол. /рузебой норабла пароход пароход пароход

Флг. 8.

Так как можно принять Р=Const. то О. с. можно охарактеризовать величиной

o)^sin?

плечом статической остойчивости. При вычислении ρ_φ сделанное выше допущение о равенстве тр-ков, заштрихованных на фигуре 1, не будет иметь места, а потому приведенные выводы следует приложить отдельно к входящему и выходящему клину. Поэтому формула (2) примет такой вид:

L

θφ=Υν /^(а« ^{+ Ь}‘^{3) dx}’ о где а,—ординаты входящей, а Ь,—выходящей из воды части грузовой ватерлинии. Кроме того мгновенная ось вращения, проходящая всегда через ц. т. грузовой ватерлинии, сместится на величину

W-V)dx,

о где Si? — площадь действующей грузовой ватерлинии, равная f (а,- + b_f)dx. Поэто-о му получим

βφ — е<р--,

£ ^{2 4} гг. где _в— поперечный метацентрический радиус, вычисленный без учета смещения оси вращения на величину ξφ· Само вычисление βφ для каждого наклонения производится но форме, данной в таблице 2.

Таблица 2. —Форма для вычисления остойчивости при конечном угле крепа.

шпан гоутов г	Входящие ординаты <4	Выходящие ординаты bi	100	b? Too	a? 1 000	bf 1 000
1
2
9
Суммы	Σα*	Ibi		lb}	Ια® •	lb}

Знаменатели 100 и 1000 вводятся для упрощения расчета, в к-ром следует выписывать лишь четыре значащих цифры. По правилу Чебышева (при 9 ординатах) получим:

. _ 100 ΣΟ - Щ.

2 Σα, + ’

•ί-£ΐ“(Σ«+2«)·

Для низкобортного корабля, когда кромка борта входит в воду, ординаты а,· и Ь,·, снятые с чертежа от точка О (фигура 9), вызовут ошибку в результате; поэтому предварительно определяют изменение осадки, к-рое необходимо сделать для каждого угла крена, чтобы сохранить V=Const·, т. к. при неравенстве клиньев входящего и выходящего это условие нарушается. Величина изменения осадки выражается следующим равенством:

само вычисление производится по таблицам методом приближенного интегрирования. Проведя новую ватерлинию выше или ниже прежней, снимают ординаты а и b) от точки пересечения грузовой ватерлинии и действующей; дальше вычисление производят как указано выше. Описанный метод Ваг-nes’a, обработанный академиком А. Н. Крыловым, не единичен. Не касаясь методов инженера Р. А. Матросова и инженера Н. К. Арцеулова [*], остановимся кратко на способах Fellow и Middendorf’a. При первом

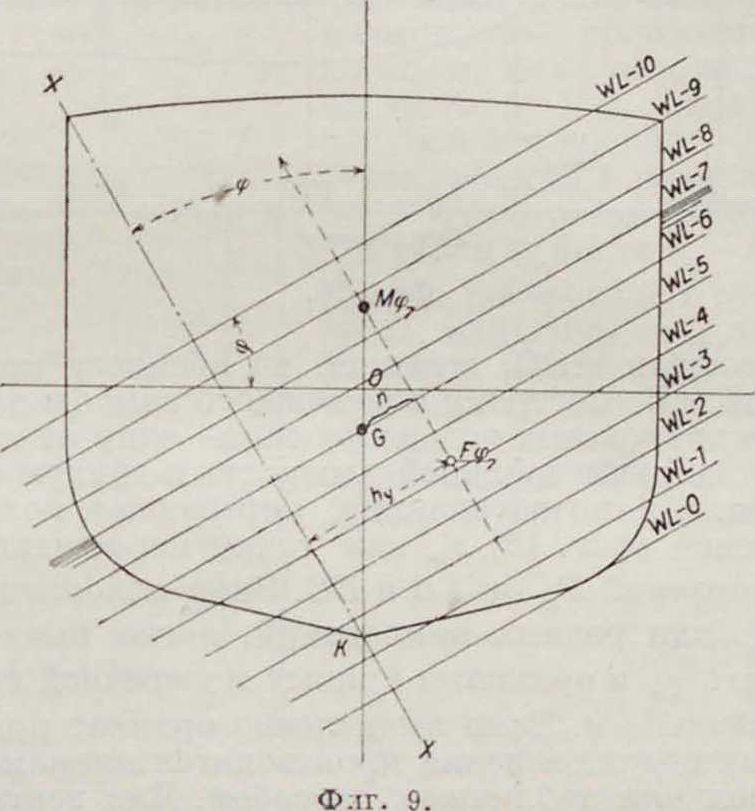
способе на теоретич. чертеж накладывают-две восковки: одну с градусной сеткой через·-10° центром на точку К, другую с серией ватерлинии перпендикулярно оси наклонения XX (фигура 9). Для каждого угла наклонения φ и каждой ватерлинии измеряют интегратором подводные площади шпангоутов и их моменты относительно оси XX. Затем находят водоизмещение и момент его относительно той же оси для каждой ватерлинии; деля второй на первое, получают плечи h_vобъёма подводной части судна для данного угла крена и данной ватерлинии относительно точки К. Откладывая их как ординаты на абсциссах, соответствующих водоизмещению· для измеренного случая, и, соединяя точки для одного угла крена, получают серию поперечных кривых остойчивости (фигура 10). Откладывая по оси абсцисс углы крена, а по оси ординат плечи и взяв в качестве параметра водоизмещение, получают для каждого водоизмещения кривую плеч h_y в функции угла крена. Для получения величины плеча остойчивости 1 φ=(ρφ — а₀) sin φ пользуются следующей формулой

Этот способ дает серии плеч остойчивости для различных осадок. Для военного корабля проще вычислить значения ρ_φ по способу, предложенному Barnes’oM, а поправки к ним по способу академика А. Н. Крылова.

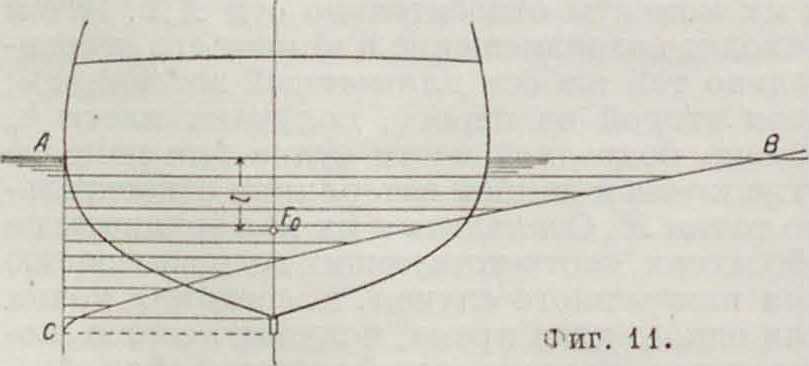
Способ Middendorf’a основан па следующем свойстве интегральной кривой. Если (фигура 11) от киля построить кривую водоизмещения до действующей ватерлинии, то отстояние ц. в F₀ от последней I будет равно

Водоизмещение

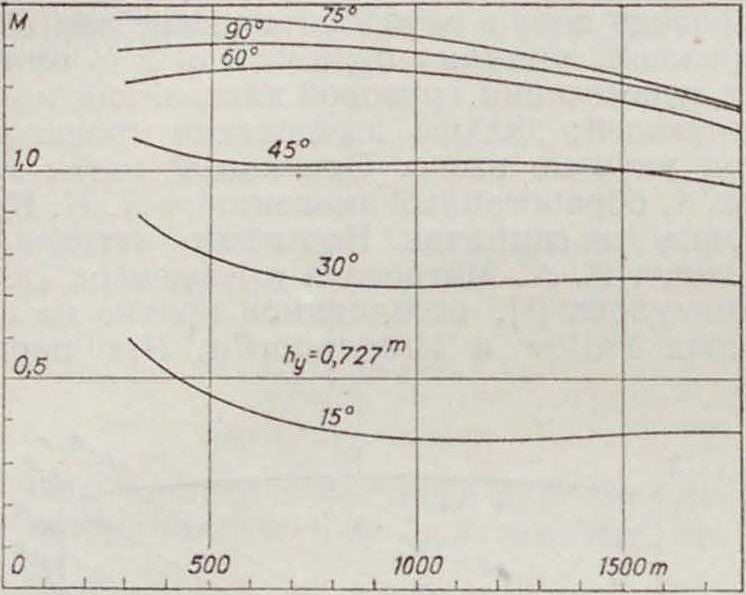
Фигура 10.

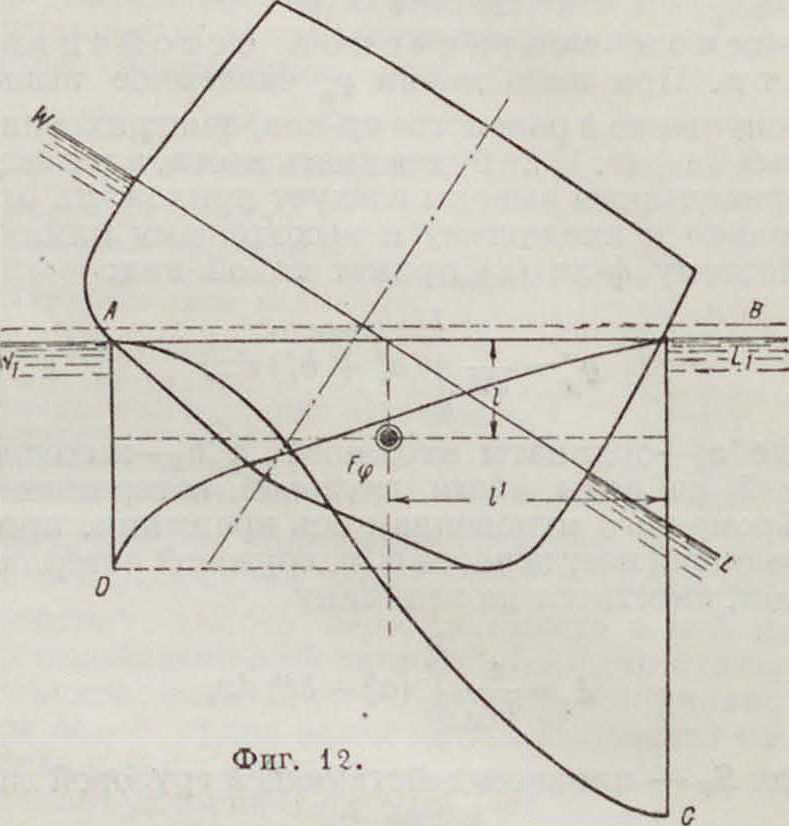
площади АВС, деленной на абсциссу кривой АВ. Построив для каждого наклонения по две кривых водоизмещения—одну от киля по диаметральной плоскости и другую от точки А по ватерлинии, определяют положение (фигура 12) F как точку пересечения отстояний F₉ от А В и ВС. Зная положения F.для разных наклонений, легко вычислить ρ_φ и ординаты кривых поперечной остойчивости. Само вычисление ординат кривых водоизмещения производится планиметром или табличным способом. Для вертикальных прямых бортов можно пользоваться приближенной ф-лой:

= (i?o - %) Sin φ + ρ₀ Sin φ (5)

4) Диаграмма Рида. Отложив по оси абсцисс углы наклонения, а по оси ординат соответствующие плечи остойчивости,

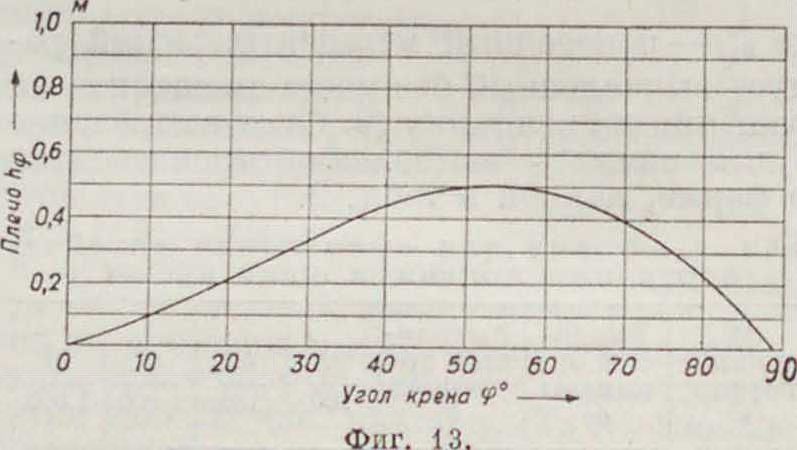
получим кривую изменения плеч остойчивости в зависимости от угла наклонения, т. н. диаграмму Рида, или диаграмму статич. остойчивости (фигура 13). Эта диаграмма дает полную характеристику остойчивости корабля при различных углах наклонения для данных водоизмещения и положения ц. т. корабля; ее ординаты пропорциональны выпрямляющему моменту, поэтому она представляет способность корабля к выпрямлению. Из фигура 13 например видно, что восстанавливающий момент растет по мере увеличения угла наклонения до ~52°, далее он начинает уменьшаться, и при 89° восстанав ливающий момент равен 0, то есть при этом угле крена после прекращения действия возмущающей силы корабль остается в положе

нии безразличного равновесия, а если на него подействует новая сила, то корабль опрокидывается. Так как член a simp в основной формуле (1) возрастает до 90°, то падение-кривой зависит от формы кривой пер

вого члена ρ_φ sin φ. Кривая значений ρ_φ в зависимости от угла крена дана на фигуре 14, из которой видно, что падение кривой ρ_φ начинается после входа в воду кромки борта, выход из воды скулы противоположного борта

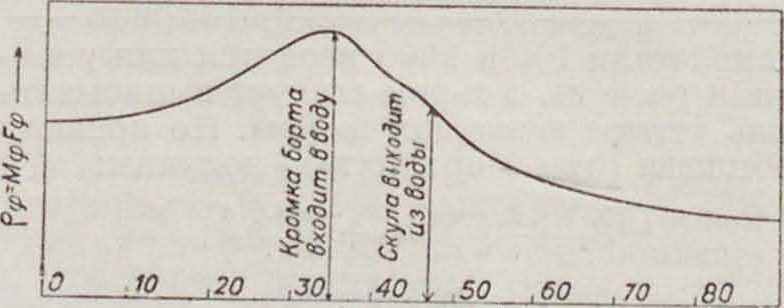
-► Угол крена Ψ

Фигура 14.

еще более усиливает падение кривой. Таким образом правильно построенный и нагруженный корабль не переворачивается и безопасен до крена, при котором кромка палубы входит в воду.

Ф-ла (5) м. б. представлена т. о.: h=))„+ Ah/, член h₀—плечо начальной метацентрич. остойчивости [h₀=М₀6₀ &ίηφ=(ρ₀—α₀) singsj и

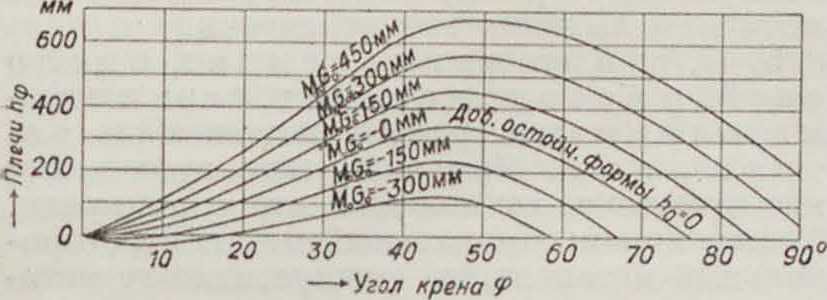
h_A — плечо добавочной остойчивости формы разно влияют на характер кривой Рида. На фигуре 15 вычерчены кривые h для одних и тех же значений h_A, но для различных положений д.т., то есть для различных M₀G₀. Пле-

Фнг. )5.

чо начальной остойчивости />₀ определяет величину статической остойчивости, характер же изменения остойчивости при конечных углах крена зависит от члена h _й. Влияние этого члена у судов различных типов на плечо остойчивости 1ι_φ

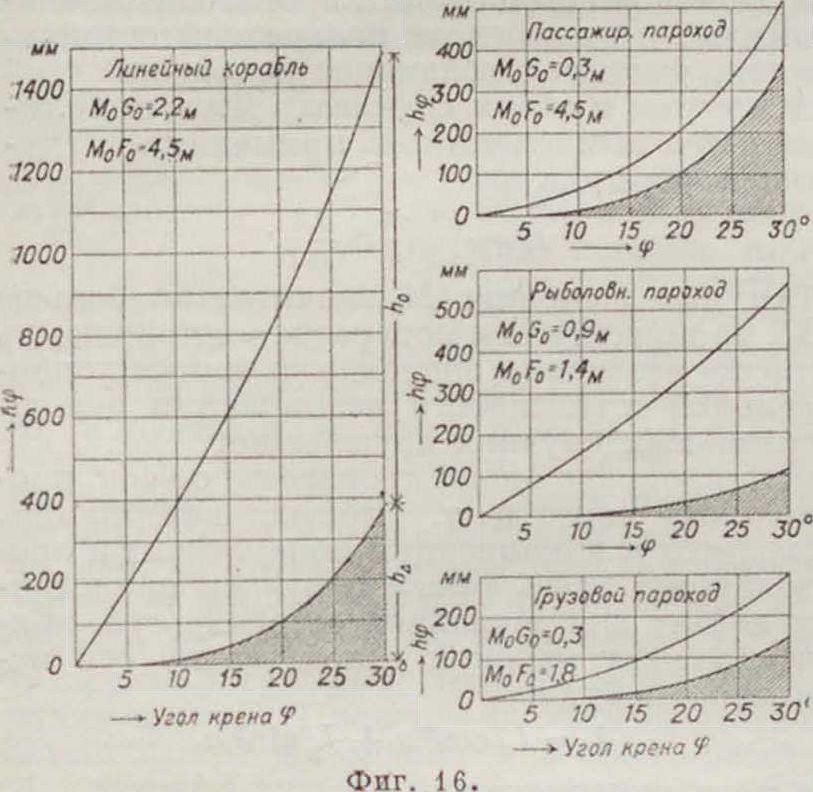
видно из фигура 16. Наибольшую остойчивость имеет судно при большом ρ_φ — а₀ и большом ρ_φ, однако это вызывает резкую качку, поэтому значение величин ρ_φ и ρ₀ — а₀ ограничивается известными пределами, смотря по типу и условиям службы корабля. Для военных судов обе величины должен быть большими, учитывая боевые повреждения (это однако влияет на меткость стрельбы при качке), океанские суда должны иметь большое ρ_φи небольшое ρ₀ — а₀. Рыбачьи суда, учитывая прием рыбы, должны иметь большую ρ₀-«ο ¹¹ малое ρ_φ, наконец обычные грузовые суда могут иметь обе величины небольшими. На фигуре 15 обе нижних кривых показывают, что судно может не опрокидываться, имея (ρ₀ - я₀) < 0 до некоторого угла крена М <0, но далее он увеличивается, корабль в этом случае имеет лишь в положении свободного равновесия нек-рый постоянный угол крена. На фигуре 17 дано взаимное отношение членов h₀ и h_A. Зависимость между величинами ρ₀ — а₀ и h становится еще яснее из фигура 18. Угол наклона кривой Рида в точке Я м. б. вычислен из соотношения:

а так как то tg α=

* 6h

h=(θ_φ - α₀) sin φ,

- α)sin?

~_Λ——; при малом угле накло нения от точки Я:

6_φ - «„=Const и tg α= (ρ_φ - а₀) =

= (β_φ - я₀) COS φ

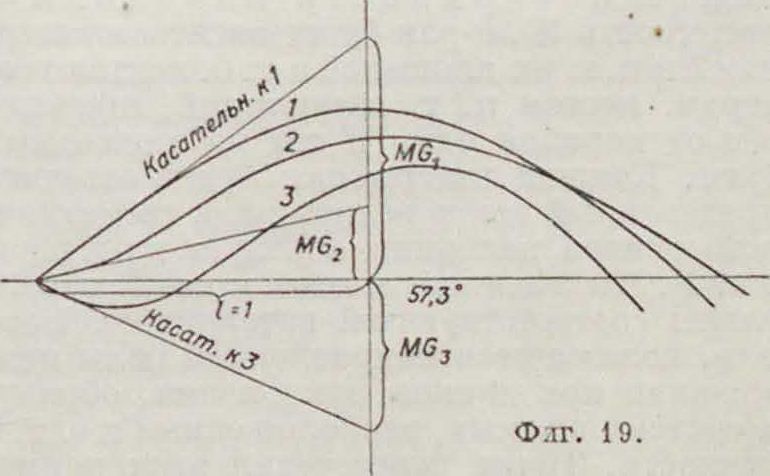
при φ=0, tg α= ρ, - а₀, то есть тангенс угла наклона кривой Рида к оси абсцисс в любой точке есть метацентрич. высота для данного наклонного положения корабля. Если отложить по прямой НВ, параллельной оси абсцисс, отрезок, равный 1 радиану (57,3°), то отрезок СВ будет равен tg а или ρ_φ - а. Сделав построение в точке О, найдем ρ₀ — σ₀, начальную метацентричес-кую высоту (фигура 19) для разных кривых статич. остойчивости MG_lt MG₃, MG₃. Из фигура видно как

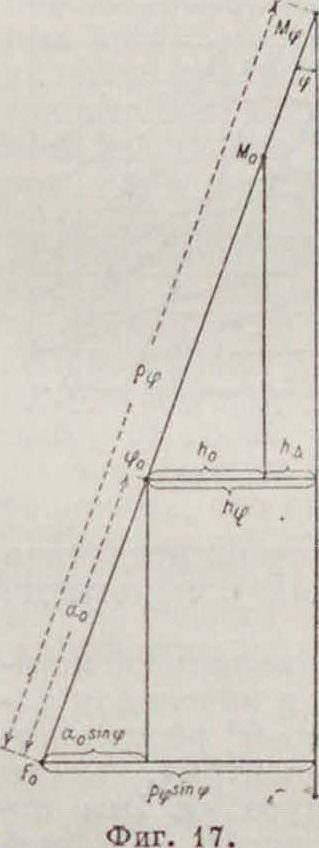
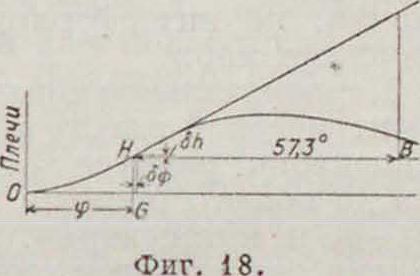
Со — а₀ определяет характер кривой. Для су-жденияобостойчивости при постоянном угле крепа φ нужно исходить из точки Я, соответствующей этому углу крена (фигура 18). Величина ρ_φ— а₀ характеризует относительную сопротивляемость корабля дальнейшему на

клонению при разных углах крена. Серия кривых Рида для судов разных типов приведена на фигуре 20: а—броненосный крейсер, 7=30 000 т, Μ„β=2,Ί м; б—линейный корабль, 7=26 000 т, M₀G =2,1 м; в—малый крейсер, 7=6 000 т, M₀G=(766 м; г—миноносец при 7=2 000 т, 1И₀Сг=0,88; 0—то же судно при 7=1600 т, M₀G=0,80 м;

e—крупный пассажирский пароход, M_nG==0,66 jvi; ок—то же судно, но принимая при расчете во внимание наличие палубных надстроек; з—средний товаро-пассажирский пароход, Ж₀б£ 0,3 м; и—грузовой пароход, M₀G=0,2 м; к—употребительная в Англии форма кривой для грузовых пароходов средней величины, M₀G=0,25 ж; л—грузовой пароход с нагруженным на палубе лесом при плавании по Балтийскому морю, iU_oG=0,

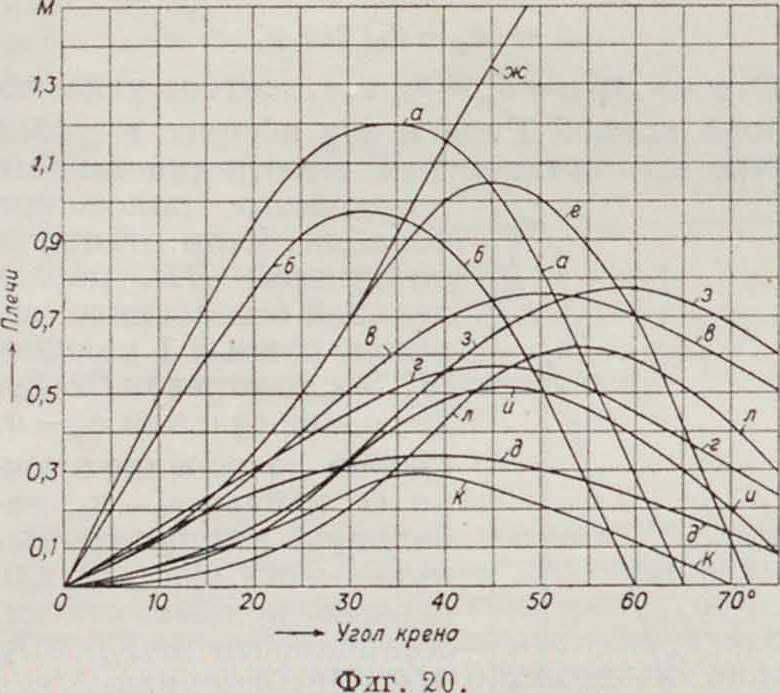
вследствие чего получается очень медленная качка, не интерферирующая с короткими волнами моря.

Первоначальное понятие о начальной мета-цонтрической высоте ρ₀ - а₀ и начальном ме-тацентрич. радиусе ρ₀ при у=0° расширяется до общего понятия метацентрич. высоты θφ-α₀ и метацентрич. радиуса ο_φ. Эти понятия связываются геометрически с формой корабля, единственным геометрическ. свойством которого является симметрия относительно диаметральной плоскости. Проводя ряд плоскостей,отсекающих от корабля один и тот же подводный объём V при разных углах наклонения и построив огибающую этой системы плоскостей, мы получим ци-линдрич. поверхность плавания — поверхность W, которая будет касаться ватерлиний в ц. т. их площадей и т. о. явится геометрии. местом ц. т. ватерлиний, отсекающих от корабля один и тот же подводный объём. Каждой ватерлинии будет отвечать определенный центр величины, а геометрии. место центра величины образует кривую ц. в F. Касательные к этой кривой параллельны соответствующей ватерлинии. Нормали, являющиеся направлением силы поддержания при данном наклонении, образуют систему прямых, расположенных в одной плоскости. Точки пересечения этих нормалей образуют эволюту кривой F, которая называется метацентрической кривой и является геометрии, местом центров кривизны кривой К.Т. о. истинный метацентрич. радиус является радиусом кривизны кривой F. Метацентры, находясь па метацентрич. кривой, не лежат на одной прямой, и т. о. определение метацентра как точки пересечения силы поддержания с диаметральной плоскостью правильно только в отношении начального метацентра, а в общем случае истинный метацентр есть центр кривизны кривой К.Опуская из ц. т. корабля перпендикуляры на метацентрические радиусы и найдя геометрии, место их оснований (подножная кривая метацентрич. кривой), получим т. н. полярную диаграмму остойчивости, дающую величины h<p чисто геометрически.

5) О. с. при наклонениях около осей, несовпадающих с главны-м и ося м и инерции площад и в а-терлннии. При диференте происходят качественно те же явления, что и при крене. Также имеем: продольный метацентр, продольный метацентрич. радиус, высоту метацентра над ц. т. судна и продольную мета-центрическую высоту. Начальная остойчивость характеризуется восстанавливающим моментом:

1/_г=Р(Д₀-а„) sin ψ,

причем R= у“, где 1_у—момент инерции грузовой относительно поперечной оси, проходящей через ее ц. т. Вычисление элементов продольной остойчивости производится аналогично с элементами поперечной остойчивости, учитывая различное положение осей симметрии в обоих случаях. Для приближенного вычисления R применима следующая формула

R =

L² V²

иг а

L-

14 Г

Так как величина М_г значительно больше М, то практически поперечная остойчивость нмрет решающее значение, и вопросы продольной остойчивости возникают в исключительных случаях службы корабля.

Наклонение около произвольной оси, проходящей через ц. т. площади ватерлинии, сводится к наклонениям поперечному и продольному; здесь также получаем аналогичную формулу для начальной остойчивости, причем момент инерции относительно осп наклонения будет

1_а=l_x cos² а -f l_y sin² а, а угол наклопения

Θ — <р cos а + у sin ^α>

где α—угол наклона оси наклонения к диаметральной плоскости (оси λ). Геометрич. рассмотрение вопроса приводит к заключению, что поверхность центров (то есть поверхность,касательная к ватерлинии при различных наклонениях корабля) имеет плоскость наименьшей и наибольшей кривизны, которые совпадают с диаметральной и поперечной плоскостью, проходящей через ц. т.

6) Динамическая О. с. Изложенная выше часть учения об О. с. рассматривает вопрос, исходя из условия равновесия между моментами кренящим и восстанавливающим. Если первый Mr больше второго М, то судно продолжает крениться до достижения равенства М_R= Μ_φ, при некотором угле крена у. Если Μ_η<Μ_φ, то судно выпрямляется до угла крена у, удовлетворяющего равенству Μ_κ=Μ_ψ^. Зная максимальную величину Mr для данного судна в его районе плавания, легко определить достаточность остойчивости этого судна. В действительности уравновешивание моментов-

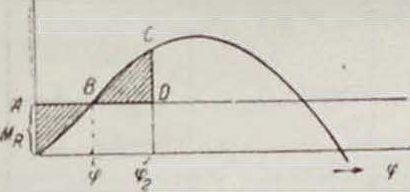
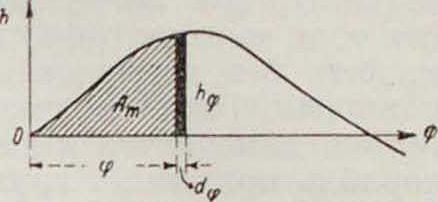
происходит динамически, в движении, что вносит в учение об остойчивости нек-рые поправки. Для этого рассматривают не только силы и моменты, действующис на корабль (статику вопроса), но и движения самого корабля (кинематику) и связь между ними (динамику остойчивости). Т. к. возмущающая сила и опрокидывающий момент вызывают качку корабля, то кинематика остойчивости •относится к учению о качке (смотрите Теория корабля). Динамич. подход к вопросу будет состоять в рассмотрении работы, как опрокидывающего, так и восстанавливающего моментов. Если откладывать по оси абсцисс путь, пройденный телом (углы поворота корабля), а по оси ординат—действующие величины силы (величины, пропорциональные восстанавливаюнщммоментам,—плечи остойчивости), то площадь между кривой нарастания силы, осью абсцисс и ординатой на нек-ром участке пути даст (в нек-ром масштабе) работу силы. При наклонении любым переменным по времени кренящим моментом M_R (фигура 21) корабль приходит к положению статнч. равновесия В с некоторой конечной живой силой, равной разности работ на данном участке кренящего и восстанавливающего моментов (то есть площадь ОАВ);в силу инерции корабль продолжает крениться дальше до угла <р„, пока вся живая сила не будет истрачена на преодоление работы восстанавливающего момента, то есть пока площадь ВДС не будет равна ОАВ. Затем корабль начнет выпрямляться, перейдет снова с той же живой силой точку равновесия и отклонится до начального положения и т. д., пока в действительности вся энергия не будет затрачена на преодоление различных необратимых сопротивлений (трения, волнообразования и т. и.). Площадь диаграммы статич. остойчивости до ординаты у даст работу А_т, затраченную на накренивание корабля на этот угол. Из фигура 22 имеем:

φ φ

А_т=j >^}V Λφ=P J (ρ_φ - a₀) sin φ dtp. о 0

Для малых углов ρ_?=ρ₀ и φ

Am₀= f Ρ(6φ-α₀) sin φ άφ=>

Фигура 2i.

= .P(eo-«o)smytg*.

Связь между M и А_то будет такая:

А_Я~М- tg$. (G)

Аналогично моменту статич. остойчивости можно написать:

Ащ~ Р * Ί"φ »

где τ_φ называется плечом динамич. остойчивости.

7) Практическое значение диаграммы Рида. Нормальные условия плавания корабля не должны допускать крена большего, чем угол, соответствующий ма ксимуму диаграммы Рида, нисходящая ветвь которой предназначается для погашения случайных динамических моментов. Площадь кривой Рида должен быть достаточна для погашения энергии возможного на практике опрокидывающего момента. При динамическом исследовании О. с. существенное значение имеет избыток работы кренящего момента по сравнению с восстанавливающим на протяжении того же угла крена. Поэтому если корабль уже был ранее наклонен некоторым моментом M_R до угла φ₁ и после этого к нему был приложен увеличенный момент М" (например порыв ветра), то увеличение крена (до у₂. по условию равенства площадок а; и Αχ) будет значительно меньше, чем в том случае, когда этот увеличенный момент начал бы действовать на ненакрененный корабль (до угла <р₃, по условию равенства площадок А_г и А). Особенно опасным для корабля является тот случай, когда он накренен моментом M_R" на один борт, а затем моментом М_R, например силой шквала с подветра, он будет переложен на другой борт. В этом случае (начальный угол крена у₄) кинетич. энергия корабля выражается всей площадью А₃ и легко возможно, что незначительные сами по себе } глы наклона могут повести к перевертыванию корабля, т. к. площадь А может оказаться недостаточной для поглощения всей живой силы корабля. Для такого случая судно с отрицат. остойчивостью в прямом положении может оказаться более надежным, т. к. при равном запасе динамич. остойчивости расходование ее на переворачивание судна на другой борт меньше, опасность опрокидывания тоже меньше. Отсюда понятно, что О. с. характеризуется не только h_max, но и <р_тпх, при к-ром плечо статич. остойчивости вновь становится равным нулю. Эти характеристики приведены в таблице 3.

Таблица 3.—X арактеристпкиостойчпво-стп судов раз лично го типа.

Класс пли тип судна	hf/iax* м	Фтах» град.
Малые грузовые и рыбачьи суда..	0,30	70
Парусные суда.	0,40	75
Грузовые ».	0,50	75
Товаро-пассажирские.	0,70	75
Траисатлантики.	1,00	72
Эскадренные миноносцы.	0,35	75
Легкие крейсеры.	0,75	75
Линейные корабли.	1,00	СО
Крейсеры..	1,20	65

8) Изменение О. с. при изменении первоначальных условий. Приведенные ф-лы и расчеты дают возможность вычислить элементы остойчивости для любого корабля при проектной нагрузке. На грузовых судах однако нагрузка резко изменяется по величине и распределению при погрузке и выгрузке грузов. Поэтому знания величины ρ„ — а₀ недостаточно, и необходимо еще иметь диаграмму, позволяющую быстро определять ρ₀ — α₀ для различ

Фигура 22.

ных случаев нагрузки. Для этой цели для грузовых судов изготовляют диаграмму, дающую положение точек F₀ и М₀ при различной осадке, и на ней же наносят положения точки G₀ при погрузке различных грузов. Эта т. н. метацентрич. диаграмма позволяет сделать без затруднений все необходимые подсчеты. Точно так же при изменении нагрузки изменяется и диаграмма Рида. Если корабль принимает груз больший, чем 12— 15% водоизмещения,то необходимо весь расчет остойчивости сделать заново, учитывая новое положение центров G₀ и F₀. Если принятый груз меньше указанного %, то добавочный расчет упрощается, т. к. действующие ватерлинии при одном и том же угле крена будут весьма близки друг к другу и их моменты инерции можно считать равными. Это обстоятельство позволяет получить новые значения метацентрического радиуса V

умножением на у-_{+ ду}, что делается просто на]счетной линейке. Если корабль принимает жидкий груз, то дело усложняется тем, что при крене он переливается, а следовательно в расчетные ф-лы следует ввести поправку на перемещение ц. т. корабля при крене. Так как перемещение клиньев на фигуре 7 вызывает увеличение восстанавливающего момента М, а перемещение жидкого груза вызовет увеличение опрокидывающего момента, то можно считать, если жидкий груз вода, что

6l~ Qa Αρ ⁼ у у »

т. к. определение Δ_ρ аналогично определению ρ₀, если г—момент инерции свободного уровня жидкого груза; отсюда 7-1

Ql~ у

Если жидкий грузпоявляется в результате затопления всего или части отсека, то изменение метацентрич. высоты будет след.:

А о G=(ρ₁ di) (ρ_ρ ^— do)» где di—новое возвышение ц. т. над ц. в Если вода заполнила отделение целиком и не имеет сообщения с зной, то

= do) + ‘-г]. (7)

При тех же условиях, но если вода в отделении переливается, то

ШЖ - ΔΜοΟ_ι - у;

если вода имеет сообщение с зной, [то Δ ЛЩ-f

Во всех ф-лах Р и V—первоначальный вес и подводный объём корабля, р—вес воды и г—высота относительно G₀ ц. т. объёма влившейся воды, ε—переуглубление, Т—основное углубление судна, -i, s и b—момент инерции, площадь и расстояние ц. т. свободной поверхности жидкости в затопленном отделении от ц. т. корабля. На южноамериканских трансатлантиках громадный расход угля к концу рейса понижает начальную и статич. остойчивость, во избежание чего по борту устраивают специальные наделки, части которых служат наружными цистернами Фрама; действие этих наделок максимально при 9>=0°. Другим способом увеличения О. с. является приемка балласта, понижающая положение ц. т. корабля; это средство дает максимальный эффект при 90° крена; т. о., целесообразно комбинируя оба средства, можно достигнуть желаемых результатов.

Вначале было упомянуто, что изменение других мореходных качеств влияет на О. с. Так, изменение пловучести, то есть увеличение или уменьшение осадки, зависящее от приема или расходования груза, уже рассмотрено. Изменение силы поддержания на волнении вследствие инерции поднимающегося и опускающегося ц. т. корабля имеет большое значение при боковой качке. На вершине волны благодаря этому О. с. уменьшается, на подошве—возрастает. Для средних грузовых пароходов при падении силы поддержания на 8—10% метацентриче-ская высота уменьшается иногда до нуля, что особенно опасно для рыбачьих судов.

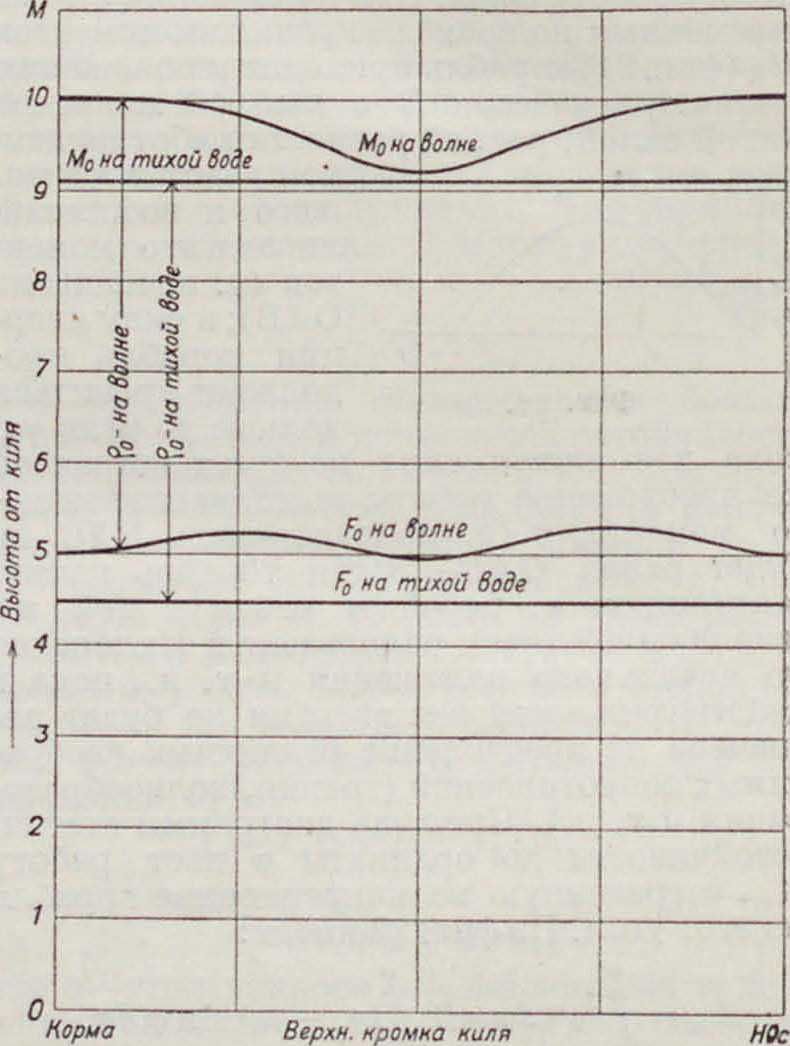
Фигура 23.

Изменение формы грузовой ватерлинии и положения ц. в при килевой качке особенно сильно при волне, идущей от носа к корме. Вообще это изменение повышает положение ц. в Момент инерции грузовой ватерлинии на вершине уменьшается, на подошве увеличивается, и ρ в среднем остается неизменным, a MG—увеличивается; фигура 23 дает картину изменения положения центров при этом в зависимости от положения гребня волны относительно длины судна. Влияние хода корабля на остойчивость зависит от волн, поднимаемых па ходу, и динамич. действия частиц воды. При увеличении волнового сопротивления на больших ходах численно изменение положения метацентра достигает, например у эскадренных миноносцев, 10 см, у глиссеров и амфибий значительно больше. Кроме того работа вин тов создает некоторый опрокидывающий момент. Влияние поворотов сказывается в создании крена, изменяющего начальные условия остойчивости. Рассмотрение условий остойчивости, особенно при больших углах крена, приводит к заключению о значительном благоприятном влиянии на остойчивость надводных частей и надстроек корабля, входящих в воду по мере увеличения крена.

Особо следует остановиться на изменении остойчивости при диференте, когда часть палубы заливается водой. В этом случае 1 может настолько уменьшиться, что судно перевернется. Поэтому для сохранения остойчивости необходимо избегать возможности этого устройством водонепроницаемых отсеков и гл. обр. доведением переборок до главной палубы (смотрите Ήепотопляемостъ).

9) Факторы О. с. Влияние главных размеров корабля: L—длины,В—ширины и Т—углубления м. б. учтено след, образом. Из ф-лы ρ₀=/:Ε, пользуясь ее приближенным значением

Со ~ Sr²: V

при изменении ширины В па В₁^пВ, получаем

ρ„=£n(rn)²: Fn;

отсюда

ρό: ρ=η³: η=η².

Τ. е. метацентрич. радиус, а при α= Const и метацентрич. высота возрастают пропорционально квадрату увеличения В. Точно так же можно получить, что изменение L не влияет на ρ₀ и ρ₀ — α₀, и эти величины возрастают обратно пропорционально увеличению осадки. Если изменяются одинаково все размеры, то

ρ„=Sn²(m)·: Fn³=ηρ₀.

Точно так же восстанавливающий момент М¹ при изменении ширины будет:

Λ/ι - Fn hn*=ΑΓη“,

то есть изменится пропорционально кубу изменения В.

При изменении одного L имеем М“=Мп, т. e. М¹¹ меняется пропорционально изменению L.

При изменении осадки Т имеем: М^ш=М и при изменении всех размеров: Μ^ιν=Μη⁴. При изменении подводных обводов судна при одновременном увеличении водоизмещения точка М₀ опускается и момент остойчивости уменьшается тем в большей степени, чем острее судно, и обратно: М₀ поднимается и момент остойчивости возрастает тем в большей степени, чем полнее судно. Если водоизмещение не меняется, то момент остойчивости остается постоянным, но М₀ опускается тем больше, чем обводы судна острее, и поднимается тем больше, чём полнее обводы судна. Из ф-лы (7) следует вывод о влиянии приема и расходования груза па ρ₀ — о₀. Величина Т + * — (ρ₀ — α₀) представляет высоту над килем такой горизонтальной плоскости, которая лежит настолько же ниже средней ватерлинии, насколько М₀ лежит выше G„. В случае если груз принимается ниже этой плоскости, ρ₀ — α„ увеличивается, если выше—уменьшается; в случае расходования груза—наоборот.

10) Использование результатов. Учение об О. с. имеет применение, кроме обычных условий службы корабля, в различных случаях его жизни, позволяя определять дальнейшее поведение корабля. Так, при посадке корабля на камень, если нос поднялся на η м, корма на к м и судно получило крен φ и диферент у>, то абсциссы точки дна, которой корабль сидит на камне, будут следующие:

х=(i?₀- α₀) _Q V и у=(ρ₀ — а₀) ~ φ, где Q—сила давления на камень=yS — т,

у—плотность воды и S—площадь грузовой ватерлинии. Точно так же место касания корабля к мели м. б. определено по изменению осадки диферента, равно как и опасность опрокидывания. Пользуясь величиной R₀— α₀, можно определить давление на блоки при постановке в сухой док. Помимо судов расчет остойчивости производится для пловучего крана и дока. Особое значение имеет остойчивость при спуске на воду судна не вполне законченного" постройкой "(смотрите Cydocmjioenne), когда неправильные расчеты могут повести к опрокидыванию судна в момент спуска на воду.

Лит.: >) Шиманский Ю. В. п Гардении Ы. Ф., Справ, книга для корабельных инженеров. Π., 1916,—К р ы л о в А. II., Учебник теории корабля, СПБ, 1913; Фа н-д е р-Ф л и т А. П., Теория корабля, ч. 1—3, СПБ, 19 11 — 16; Biles J. Н., The Design a. Construction of Ships, 2 ed., v. 2, L., 1923; Herner H., Die Theorie d. Sciiiffes, 2 Aufl., Lpz., 1921; Pollard J. et Dudebout A., Architecture navale, t. 1, P., 1890; В a t a i 1 1 e I,., Problimes de stabilite, de deplacement et d’assiette du navire, 2 ed., P., 1925; Cowell, The Stability of Ships in Practice, 2 ed., London, 1919; H 1 1 1 h о u se P., Ship Stability a. Trim, L., 1919; Rondeleux M., Stabilite du navire en eau calme ct en mer agitfie, P., 1911; J о h о w-F ocrsterE., Hilfsbuch f. d. Schiff-bau, 5 Aufl., B., 1928; Schmidt A., Die Stabllitat von Schiffen, B., 1892. P. Тишбейн.