Осциллятор

Осциллятор, в общем смысле любая колеблющаяся система. В теоретической физике обычно О. называют линейную колеблющуюся систему, например электрон, совершающий колебания по прямой линии относительно определенного положения равновесия. Если сила, заставляющая О. колебаться, пропорциональна удалению от положения равновесия, то О. называют гармоническим, или квазиупругим, в противном случае О. будет ангармоническим. Гармонич. О. является простейшей идеализированной моделью колебаний в атомах и молекулах и постоянно применяется при рассмотрении процессов распространения света в веществе и т. д. Ур-ие движения О. в классич. механике выражается так:

m^d£=-kx (1)

(х—смещение,»»—масса, к—постоянная ква-зиупругой силы). Решение этого уравнения чисто гармоническое:

®-gi.sin(j/~*:-i+a). (2)

Частота колебаний ^отсюда

b (3)

она (в этом теоретич. простота О.) не зависит от энергии движения, или амплитуды А. Энергия О. равна кинетич. энергии "его при прохождении через положение равновесия (потенциальная энергия здесь равна нулю):

Е=”* А^{5 к}=2 лта>^гА“. (4)

В теории квантов (смотрите), развитой Планком и Бором, вопрос о колебаниях О. получил иное освещение. По основному постулату Бора, фазовый интеграл:

I=^p-dx=nh (5)

(где р—импульс, h—постоянная Планка, n=0, 1, 2, 3, .). Из ур-ий (2), (3) и (4) следует, что для 0.4= ~, то есть

Е=»hto, (6)

иными словами, энергия О. должна быть кратной целого кванта luo.

В новой квантовой механике теория О. изменяется. Основное волновое ур-ие Шре-

дингера (смотрите Кванты) принимает в данном случае вид:

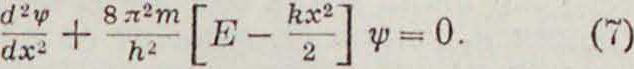
Непрерывное и исчезающее в бесконечности решение этого ур-ия возможно только для дискретною ряда значений энергии:

E-(n + )ha. (8)

В отличие от превшей теории квантов (6) здесь входят половинные значения кванто вых чисел. Этот результат согласуется с экспериментальными спектроскопическими данными.

Лит.: Д а p р о у К., Введение в волновую механику Шредингера, «УФЫ», 1929, вып. 9, стр. 437; S о m m e r f e I d A., Atombau und Spektrallinien, Welleninechanisclier Ergiinzungsband, Braunschweig, 1929; Planck M., Vorlesungen iiber d. Theorie d. Wirinestrahlung, 5 Aufl., Lpz., 1923. С. Вавилов.