> Техника, страница 68 > Отдача артиллерийских орудий

Отдача артиллерийских орудий

Отдача артиллерийских орудий,

импульс силы давления овых газов на затвор орудия, равный количеству движения, приобретаемого орудием в процессе выстрела. По закону сохранения движения ц. т. свободной группы тел остается в покое или движется прямолинейно с постоянною скоростью до тех пор, пока действующие силы, перенесенные в ц. т. группы, остаются в равновесии. Закон этот применим ко всякому огнестрельному орудию, т. к. каждое из них можно рассматривать как группу тел (снаряд, само орудие и т. д.), взаимное положение которых изменяется под влиянием сил давления овых газов, то есть сил, которые, будучи перенесены в ц. т. группы, остаются в равновесии. Силу трения орудия о землю, не превышающую в обычных условиях 0,01 доли силы давления овых газов, можно не принимать в расчет. Если орудие перед выстрелом находилось в покое, то и во время выстрела ц. т. группы останется в покое, то есть перемещение тел группы будет происходить во взаимно-противоположных направлениях и расстояние каждого из них от начального положения будет обратно пропорционально массе этого тела. Если например масса орудия в 100 раз больше массы снаряда и тел, движущихся вместе с ним, то перемещение снаряда вперед будет приблизительно в 100 раз больше перемещения орудия назад. Это движение орудия-явление нежелательное.

В интересах правильности наводки, скорости стрельбы, избежания наката и новой наводки после каждого выстрела и т. д. необходимо было бы, чтобы орудие оставалось во время стрельбы неподвижным. Требование это практически невыполнимо, так как давление овых газов, обусловливающее движение орудия назад, настолько велико, что для закрепления последнего в неподвижном состоянии потребовались бы чрезвычайно прочные сооружения. В полевых орудиях например сила давления ов. газов обычно превышает 125 000 килограмм. В условиях, при которых приходится действовать полевым орудиям, никакое закрепление их в неподви жном состоянии при этих громадных силах давления невозможно. Величина движения орудия назад во время выстрела обусловливается двумя факторами: действием силы давления овых газов и продолжительностью этого действия, то есть импульсом давления овых газов, передаваемым орудию в направлении, противоположном движению снаряда. Импульс этот, называемый отдачей орудия, выражается интегралом г

JPdt,

о где Р—сила давления овых газов и t—продолжительность в ск. действия ее на орудие. Сила Р определяет собою величину ускорения движения орудия во время выстрела и равна ~ W, где G—вес орудия в кг, д—9,81 м/ск“—ускорение силы тяжести и W м/ск²—ускорение движения орудия. Таким образом:

₍₁₎

0 0 о где V м/ек—скорость, приобретенная орудием к концу выстрела. Отдача орудия равна следовательно тому количеству движения, которое приобретает орудие к концу выстрела.

Энергия овых газов тратится на движение орудия, снаряда, самих овых газов и того воздуха, к-рый находится в(канале ствола до выстрела. Т. к. до и после выстрела канал ствола оказывается заполненным приблизительно одинаковым количеством газов, то в дальнейшем расчете влияние воздуха в канале ствола на отдачу можно не принимать в соображение. Такой нее по величине импульс, который передается овыми газами орудию, передается ими также массе снаряда и овых газов. Как и в предыдущем случае, оказывается, что импульс силы давления овых газов равен тому количеству движения, к-рое массы снаряда и овых газов (вес последних равен весу ового заряда) приобретут к концу выстрела, то есть

Г Р di=- F + Г^Q V + ^р- U, (2) J V J я a a^,w

о о где Q—вес снаряда, V—скорость, с которой снаряд вылетает из ствола орудия, р—вес ового заряда и U—средняя скорость, с которой овые газы оставляют канал ствола. Величины Q, V и р для всякого орудия точно известны, тогда как скорость U лишь с большим трудом поддается учету. В тот момент, когда снаряд вылетает из ствола орудия, овые газы начинают также оставлять ствол, причем скорость их становится значительно больше скорости снаряда. Если бы превращение энергии овых газов в их живую силу происходило при этом целиком в канале ствола, то определение скорости U не представляло бы затруднений. Ее можно было бы определить из

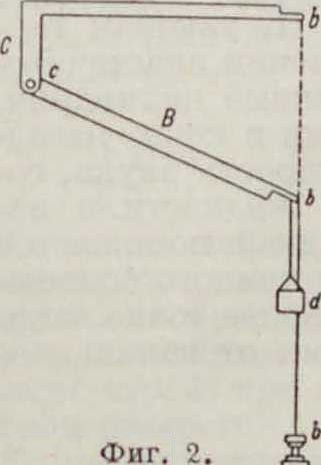
где А—потенциальная энергия, которою обладают овые газы в тот момент, ког-да снаряд вылетает из ствола, и _Q —кине-тическая энергия этих газов в тот момент, когда они обладают средней скоростью -.

По закону адиабатич. расширения газов работа А определится из ур-ия

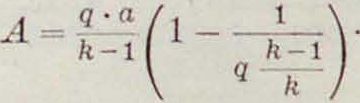
Этот закон вполне применим для данного случая, но он не применим во время движения снаряда в стволе орудия потому, что во все это время овой заряд лишь постепенно переходит в газообразное состояние, развивая энергию; в тот момент когда снаряд вылетает из ство.ча, почти весь заряд перешел уже в газообразное состояние, и овые газы переходят в такое состояние, когда энтропия их становится величиною постоянною, то есть когда дальнейшее расширение овых газов происходит по закону адиабатич. расширения.

Подставляя в это уравнение адиабат вме-

_· Jld - 7

сто объёма а канала ствола выражение — Ϊ,

i

где d—калибр орудия и I-вместо к—1,41, получим:

-длина ствола, и

А=1,915 qdH (l — >

где 7—давление овых газов в тот момент. когда снаряд выходит из канала ствола. То обстоятельство, что к концу движения снаряда в стволе незначительная часть ового заряда еще не превратилась в газ и продолжает переходить в газообразное состояние в то время, когда овые газы оставляют канал ствола, оказывает нек-рое влияние на величину А тем, что, понижая коэф. к₉ увеличивает А. Определить, как велика эта еще не перешедшая в газообразное состояние часть ового заряда, и вместе с этим учесть влияние этого обстоятельства на величину А, оказывается пока невозможным, так как на это обстоятельство влияет не только состав а, но и вес снаряда и длина ствола, от которых гл. обр. и зависит продолжительность перехода ового заряда в газообразное состояние, а вместе с тем и б. или м. полное завершение этого процесса. Итак, допустив полный переход потенциальной энергии овых газов в кинетическую по закону адиабатич. расширения газов, мы получим:

vU~ 2 д

pV 2

8 U

+ 1.915 qdH (l-^y.

При Г=500 м/ск, р =0,615, 7=350 atm., d=7,62 и I 2,3 .и средняя скорость U, с которой газы оставляют канал ствола, будет равна 1 560 м/ск. Подставляя эту величину в ур-ие (2), мы определим отдачу орудия.

Вычисленная т. о. отдача орудия оказывается больше наблюдаемой. Объясняется это тем, что не вся работа А превращается в канале ствола в кинетич. энергию овых газов, т. к. газы эти выходят из ствола орудия в виде струи, упругость κ-poft значительно выше атмосферного давления. Т. о. только часть работы А превращается в кинетич. энергию овых газов в канале ство ла и этим влияет на отдачу, увеличивая ее. Решающее влияние на превращение потенциальной энергии газов в кинетическую при истечении их в среду более низкого давления оказывает форма отверстия, через к-рое происходит это истечение. По законам термодинамики [*]., при истечении эластичных жидкостей через обыкновенные цилиндрич. насадки, скорость истечения в конце насадки не может превысить скорости звука, соответствующей состоянию жидкости в насадке, и давление в последней понижается поэтому лишь до давления немного большего половины начального. Более точно зависимость конечного давления от начального выражается ур-ием

*

91=ч (тгггГ¹ “ °’⁵·^·

Полное превращение давления газа в его скорость происходит только при истечении газа через конич. насадки. Применяя этот закон для данного случая, мы найдем, что при истечении овых газов из канала ствола, передний конец которого не расширен в виде конуса или борт отверстия которого не закруглен, давление этих газов в конце канала ствола понижается лишь до 0,53 того давления, к-рое господствует в канале ствола во время истечения. Дальнейшее понижение давления происходит вне ствола и поэтому не влияет на увеличение интересующей нас скорости U, а следовательно и на отдачу орудия. Т. о. только 0.47 давления газов в стволе превращается в их скорость внутри ствола. Поэтому и в кинетическую энергию газов внутри ствола превращается только 0,47 А. То обстоятельство, что развитие интересующей нас скорости U происходит внутри ствола, нисколько конечно не противоречит тому факту, что наибольшая скорость отдачи соответствует положению снаряда вне ствола, так как самое развитие скорости U происходит в то время, когда снаряд находится вне ствола.

На основании высказанных соображений построено нижеследующее ур-ие, служащее для определения скорости U:

рГ.г

29

^ + 0,97^1(1

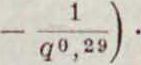
Для давлений 7 в пределах 200—600 atm величина выражения в скобках колеблется в пределах 0,80—0,86. Приняв его равным 0,83 и подставляя вместо д 9,81. мы получим:

и-У * + 14,66* <И,

где U и V—в м/ск, 7—в atm, р—в кг, d в с.м и I—в м. Ур-ие отдачи принимает т. о. следующий вид:

.f"" .ft г : ? 11,6 «уч. (2 i

о

Употребление выведенных ур-ий затрудняется тем обстоятельством, что конечное давление 7 в канале ствола не во всех случаях известно. Там, где имеются данные относительно этого давления, результаты вычисления от (ачи по формуле (2) вполне соответствуют действительности. Вычисляя скорость U но выведенной формуле для случаев, чаще всего встречающихся на практике, и для давлений η 250—500 atm, мы найдем, что скорость U колеблется в пределах 1,7F4-2,1F. В отдельных случаях U доходит до 2,0 F.

Принимая для U среднее значение равным 1,9 V, мы получим вместо ф-лы (2) более простую и годную для приблизительных вычислений во всех случаях ф-лу:

fpdt=°F + 1,9^PF=^ ^{+ 1}^F. (3)

J и a a ⁴

о

Автор настоящей статьи имел возможность проверить все высказанные относительно отдачи соображения на опытах с обыкновенным ружейным стволом. Опыты эти показали, что: 1) при обыкновенном цилиндрическом отверстии ствола скорость £7=~ 1,9 F;

2) при закруглении борта отверстия, причем радиус закругления был 1—2,5 миллиметров, скорость U доходит до 2,25 F; 3) при конич. отверстии ствола, причем длина конуса доходила до 00 миллиметров и диаметр переднего конца конуса— до 13 миллиметров, U делается равной 2,8 F и больше. По предложению Пьобера (Piobert) при вычислении О. а. о. к весу снаряда прибавляют половину веса ового заряда и приравнивают отдачу выражению —_&°^5ρ· F.

Предлагая эту ф-лу, Пьобер принимал, что на величину отдачи овой заряд влияет только до тех пор, пока он не превратится в газ. Начиная свое движение вместе со снарядом, овой заряд постепенно переходит в газообразное состояние, чтобы к концу движения снаряда в стволах окончательно превратиться в газ. Т. о. в среднем вместе со снарядом движется лишь половина ового заряда и поэтому лишь половина заряда влияет на О. а. о. Р. Вилле [²] находит, что предложенный Пьобером коэф. 0,5 слишком мал и что по данным опыта величина этого коэф. должен быть принята равной скорее 1 или даже 2. При этом Вилле считает, что «обе эти величины не могут соответствовать действительности», т. к. уже коэф. этот, равный 1, показал бы, что «во все время движения снаряда в стволе орудия овой заряд совершенно не переходит в газообразное состояние, что очевидно невозможно». Таким обр. и Р. Вилле принимает, что овой заряд влияет на отдачу орудия, находясь лишь в твердом, а не в газообразном состоянии.

Имея все данные для определения величины О. а. о., мы можем легко определить и энергию отдачи. Из ур-нй (1) и (3) имеем

g_v=Q±11?_v.

а в

Отсюда скорость v, к-рую приобретает орудие к концу выстрела,

Т. о. энергия отдачи

G<-2 (Q + 1.9p)2V? 20 ~ 2gG

(5)

Если вес G орудия 1100 килограмм, вся масса его принимает на себя отдачу, вес Q снаряда ~.2 килограмма, вес р ового зарядα= 0,7 килограмм, начальная скорость V снарядα=529 м/(К, то энергия отдачи D будет равна

Л _ (7,2 + 1,9 0,7)²529а ^U ~ 2· 9,81-1100

943 .5 килограмм метров.

Отдача этою орудия

7,2 - 1.9 · о,7 ~ 9.81

529=460

кг/ск.

Скорость

v=529

отката орудия

,2 + 1.9· 0,7 1 шо

= 4,102 м/ск.

Под влиянием приобретенной энергии орудие движется назад до тех пор, пока силы сопротивления движению не поглотят всю эту энергию. Величина отката орудия обратно пропорциональна силам сопротивления откату.

Все современные орудия можно разделить на два класса: 1) орудия с откатным лафетом, в которых все орудие вместе с лафетом принимает участие в откате и 2) орудия с откатным стволом, в которых лафет во время стрельбы остается в б. или м. спокойном состоянии, причем в откате принимает участие лишь ствол вместе с нек-рыми другими частями орудия. К орудиям первого типа относится большинство орудий полевой и отчасти крепостной артиллерии старых типов. К орудиям второго типа относится большинство морских орудий и полевые орудия современных конструкций. Увеличение скорости стрельбы обусловливает необходимость свести к минимуму откат орудий, т. к. накат орудий в положение, к-рое они занимали до выстрела, и необходимость новой наводки ведут за собой значительную потерю времени и утомление орудийной прислуги. Скорострельные в современном смысле этого слова орудия стали возможными лишь тогда, когда удалось в б. или м. степени парализовать откат и приводить орудие автоматически по возможности в то же положение, к-рое оно занимало до выстрела. В наибольшей степени этого удалось достигнуть в орудиях с откатным стволом. Относительная неподвижность лафета этих орудий дала также возможность устройства на орудии щитов, служащих для прикрытия орудийной прислуги от неприятельских выстрелов. Устройство таких щитов на орудиях с откатным лафетом бесцельно, т. к. не избавляет прислугу орудия от необходимости отходить перед каждым выстрелом в сторону от орудия из-под прикрытия щитов.

Простейшими из средств торможения отката в орудиях с откатным лафетом является тормоз для колес орудия и простой сошник. Простое торможение колес орудия хотя и уменьшает откат, но далеко не в достаточной степени. В самом деле, принимая коэфи-циент трения о землю орудия, скользящего под влиянием отдачи заторможенными колесами, равным 0,4, мы получим для нашего отката орудия

- D 943,5 ^s-" 0,4G ^— 0,4-1100

2,145 .ч.

Для торможения отката уже давно поэтому начали применять сошник. Последний представляет собою б. или м. широкую лопату, помещенную у заднего конца лафета и зарывающуюся под влиянием энергии отдачи в землю после первого же выстрела. При достаточной величине сошника реакция земли на сошник может вполне уравновесить давление овых газов на орудие и последнее не будет иметь возможности откатывать-

ся. Способ этот одпако совершенно не применим, т. к. вместо того, чтобы откатываться. орудие начинает подбрасываться вверх (фигура 1). Если а—угол лафета, то вертикаль

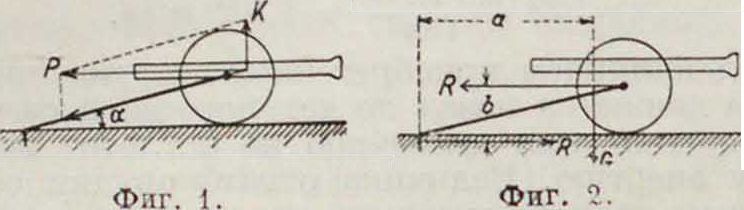
ная составляющаядавления овых газов м. б. принятой равной K=Ptga. Импульс овых газов по направлению вверх будет равен (

Р · tg а · di=® V tg а ®

^1,9р Г tg «.

Энергия подбрасывания орудия вверх равна О - tg² а. Для нашего примера, если α= 30°, Z)tg-a=943,5-0,333=314,5 к гм. Орудие будет подбрасываться вверх на высоту ^Dp ^ts^~ —

= 0,41 .w. Падая после этого вниз, орудие сильно ударяет о землю и сбивает наводку. Новая на для следующего выстрела становится необходимой. Этот недостаток быть может и окупил бы выгоды устранения отката, если бы способ этот не требовал

Фигура з. чрезвычайно прочных, а поэтому и тяжелых лафетов, т. к. силы, действующие на лафет при выстреле, и те напряжения, которые вызываются в орудии при ударах его, в особенности о каменистую или промерзшую почву, очень велики.

Волыпинство полевых орудий старых конструкций снабжалось простым сошником. Однако размеры его, выбор почвы и др. условий, при которых допускалось применение этого сошника, не позволяли ему так сильно зарываться в землю, чтобы орудие при выстреле поднималось вверх. Сошник роет в земле б. или м. длинную канавку, тормозя т. о. энергию отдачи, причем орудие не поднимается кверху. Для этого необходимо выпол-нение.условия(фигура 2): G-a^ R-b, то есть сила сопротивления почвы движению сошника

R iGj. В нашем примере при α= 1,7 метров и

Ь =0,85 метров наименьший откат орудия, при к-ром последнее не поднимается от земли, будет достигнуто при

Я =1100-^=2200 килограмм. Наименьшая длина отката равна т. о.

D 043.5 Q R 2 200 ^U

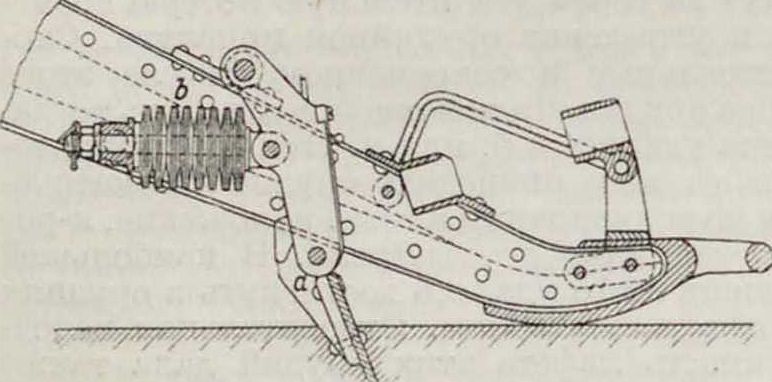
Желание использовать часть энергии отдачи, для того чтобы приводить орудие после выстрела автоматически в положение близкое к тому, к-рое оно занимало до выстрела, привело к введению так называемых эластичных сошников. Сошником этого рода снабжено значит, количество полевых орудий старого образца, находящихся и поныне в употреблении в некоторых странах. Эластичный сошник помещается также у заднего конца лафета; сошник a (фигура 3) сидит на горизонтальной оси и соединен

Фигура 4.

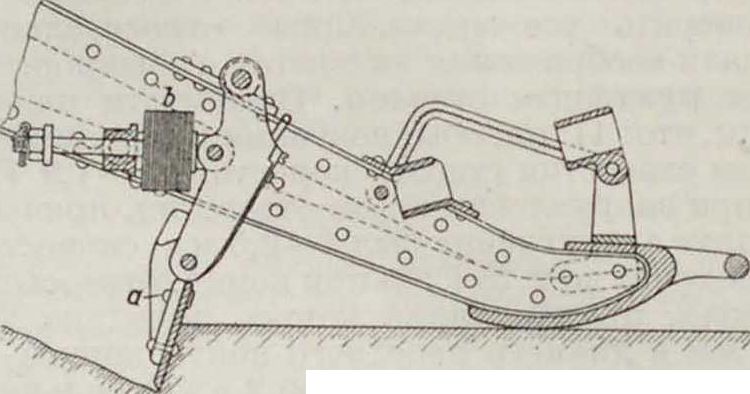
спереди или сзади с сильными пружинами Ь или резиновыми буферами. При откатке орудия(фигура4)эти пружины или буфера сжимаются сошником, движение которого задерживается землею, для того чтобы, снова расширяясь после остановки орудия, сдвинуть орудие вперед в положение, близкое к тому, к-рое оно занимало до выстрела. В момент окончания отката орудия буферные пружины совершенно сжаты. После остановки орудия пружины Ь, расширяясь, двигают орудие вперед и производят т. о. часть работы наката. Фигура 5 показывает сошник русских орудий образца 92/95 г. Сошник действует при посредстве буферной штанги а на резиновые буфера Ь, помещенные внутри заднего конца лафета, имеющего Форму коробки.

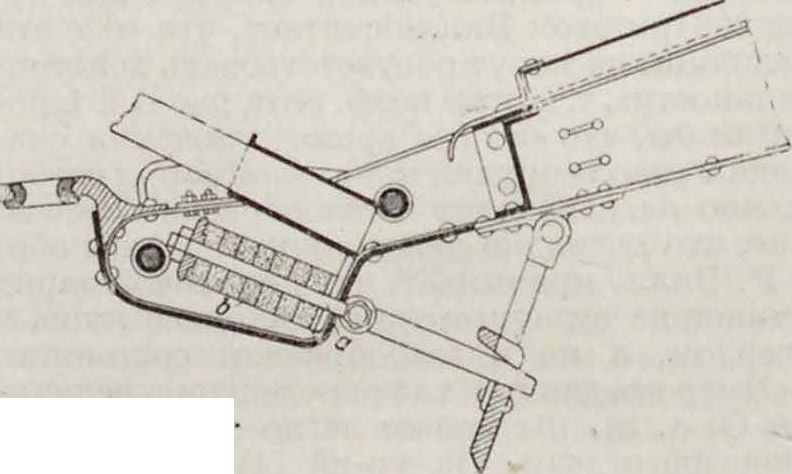
Фигура 5

Действие этого сошника аналогично действию сошника с пружиной.

В нашем примере для предупреждения движения орудия вверх необходимо, чтобы усилия, приложенные к сошнику, не превышали 2 200 килограмм. При откате орудия энергия отката поглотится работою сошника в почве и работою буфера. Величина последней должна равняться работе наката орудия, то есть kGs, где к—коэфипиент трения орудия о землю при накате. Обозначая движение сошника в землю через и его движение относительно лафета через з₂, мы получим откат орудия s=s₁ + s₂. По условию наименьшего отката

D=2200s₂ + к· G(s, + s₂).

При s,»0,2 л и fc=0,2 энергия отката D=943,5=2 200 s_t + 0,2-1 ЮО^Ч 0,2). Отсюда 0,372 .и и полный откат орудия s 0,372+0,2=0,572 метров Лишь в очень редких случаях удается поставить орудие в такие условия, при которых сопротивление почвы не только не превышало бы известного предела, но и точно соответствовало бы тому откату, к-рый м. б. осилен буфером для приведения орудия в то же положение, к-рое оно занимало до выстрела. Существует целый

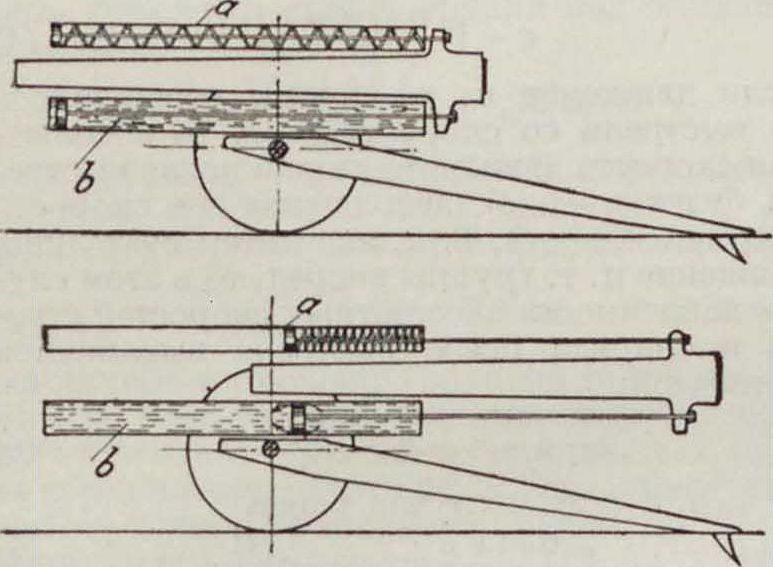
ФИГ. 6.

ряд конструкций эластнчн. сошников, которые посредством регулирования работы буфера сообразно качествам почвы стремятся сгладить этот недостаток. Все эти конструкции однако мало достигают своей цели. Полный откат старых австрийских орудий, снабженных описанным сошником, при обычных условиях бывает равен 0,8—1 м, причем буфер сошника накатывает орудие на расстояние 0,2—0,3 метров от того положения, к-рое орудие занимало до выстрела. В орудиях этого типа с резиновым буфером сошник уже после первого выстрела остается почти неподвижным в почве и орудие подбрасывается после каждого дальнейшего выстрела вверх.

Дальнейшим шагом по пути развития современных орудий явилось введение в начале 90-х гг. прошлого в полевых орудий с откатным стволом и с неподвижным лафетом. В орудиях этого типа лафет снабжен обыкновенным сошником, задерживающим его движение назад. Ствол орудия помещается на лафете так, чтобы он мог совершать под влиянием отдачи большее или меньшее движение назад, не изменяя своего направления, причем движение это тормозится посредством гидравлического и эластического воздушного тормозов (во французских орудиях), или посредством гидравлич. тормоза Ь и одной или нескольких пружин а (фигура 6), или же наконец посредством гидравлич. тормоза и резиновых буферов (русск. полевые орудия образца 1900 г.). Гидравлич. тормоз поглощает при этом большую часть энергии отдачи. Остальная часть этой энергии поглощается эла-стичн. тормозом (пружинами или воздушным тормозом или резиновыми буферами) для того, чтобы произвести необходимый накат ствола орудия. Т. к. в этом случае отдача орудия воспринимается не всем орудием, а лишь одним сравнительно легким стволом, то энергия отдачи будет здесь значительно больше. Принимая в нашем примере вес ствола и всех частей орудия, движущихся с ним, равным 390 килограмм, мы определим энергию отдачи

В =

(7,2+ 1,9 0,7)»5298 2 · 0,81 · 390

= 2 661

к гм.

Эта энергия должен быть поглощена гидравлич. тормозом и пружиною, причем силы, вызываемые этим торможением и передаваемые ла-

Фнг. 7.

фету орудия, не должны превышать предела, при к-ром орудие может стоять спокойно, не поднимаясь вверх. В нашем примере предел этот равен 2 200 килограмм. Максимальные силы торможения в орудиях с откатным стволом относятся к средним силам торможения приблизительно’как 1,3 : 1 (в русских орудиях 1900 г. отношение это менее благоприятно). Т. о. наименьший необходимый для спокойного состояния орудия откат ствола равен в нашем примере

= 1,573 метров.

1,3

Такой большой откат ствола не выполним для полевых орудий по чисто конструктив-

Фпг. 8.

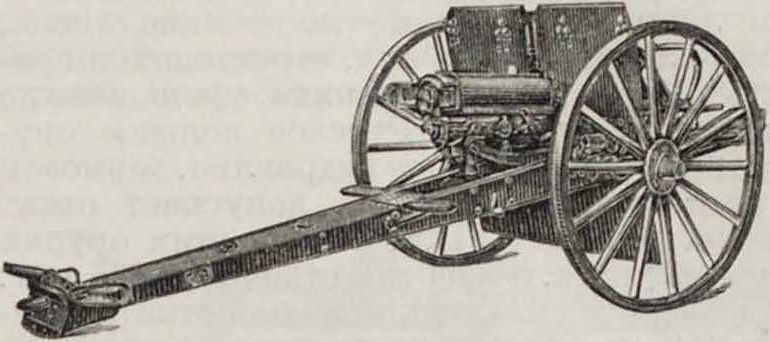
ным соображениям. Если мы примем во внимание, что длина ствола этих орудий колеблется в пределах 1,7—2,4 метров и длина лафета в редких случаях превышает 2 м, то обстоятельство это станет нам вполне ясным. Наибольшая длина отката ствола достигнута в некоторых из лучших современных полевых орудиях, например в американских орудиях (фигура 7 и 8); на фигуре 7—орудие со стволом в нормальном положении, на фигуре 8— орудие со стволом в крайнем заднем положении в момент окончания отката; длина отката равна 1,25 метров В крупповских полевых орудиях откат ствола достигает 1,36 ж. Длинный лафет в соединении с конструкцией гидравлического тормоза, допускающей очень благоприятное отношение максимальных к средним силам торможения отката, позволяет этим орудиям оставаться во время стрельбы в совершенно спокойн. состоянии.

Все попытки сделать откат ствола полевых орудий меньше 1,2—1,25 метров могут привести к успеху только при соответственном увеличении веса ствола и движущихся вме-

сте с ним частей тормозного прибора и при уменьшении веса снаряда или его начальной скорости. Во всех орудиях, энергия снаряда которых на каждый кг веса ствола равна 250 к гм (лучшие современные орудия), все такие попытки должны неизбежно окончиться неудачей. Французские полевые орудия с откатом ствола 1,09 метров по отзыву нек-рых военных специалистов стоят во время стрельбы в общем неспокойно. Спокойствие их достигается лишь при нек-ром угле подъема ствола, когда плечо момента сил, стремящихся вращать орудие вокруг сошника, уменьшено до известного предела. Русское полевое орудие 1900 г., снабженное гидравлич. тормозом и резиновыми буферами, допускает откат ствола, равный 0,91 метров Отдача этих орудий равна490кг/ск, и энергия отдачи—2 835 килограммм. При средних силах торможения отката, равных 3115 килограмм, орудия эти ни в каком случае не могут оставаться во время стрельбы спокойными. Только длинный откат ствола обеспечивает орудию спокойствие во время стрельбы.Спокойствие это достигается однако только при условии действия сошника в благоприятной почве. Если стреляющее орудие находится на каменистой или промерзшей почве, на мостовой и тому подобное., то удержать орудие в спокойном состоянии не удается и при длинных откатах ствола, т. к. сила трения орудия, скользящего по земле под влиянием сил торможения отката, значительно меньше этих сил торможения. Короткий откат ствола, задерживаемый сильным торможением, возможен только там, где возможно прочное закрепление лафета орудия, как например в морских и крепостных орудиях. В большинстве случаев здесь возможны прочные сооружения, выдерживающие силы торможения даже при сравнительно незначительных откатах ствола.

Чтобы дать понятие о силах, поглощаемых при торможении энергии отдачи больших орудий, приведем для примера круп-гговское 24-с.м орудие. Вес ствола этого орудия равен 25 600 килограмм; вес снаряда—215 килограмм; вес ового заряда—74,5 килограмм и начальная скорость снаряда—867 м/ск. Энергия отката ствола

(215 + 1,9 · 74,5)2 · 897

= 192 275 килограмм/м.

2-9.81-25 600

Средние силы торможения отката при длине его в 1 метров должен быть равны 192 275 килограмм. Как было упомянуто, даже наибольшие откаты ствола в 1,25 метров далеко не во всех случаях обеспечивают спокойное состояние полевых орудий во врем51 стрельбы, при которых орудие не выходит из данного ему наводчиком направления. Есть один способ избавиться от этих затруднений, допускающий применение коротких откатов ствола при незначительных силах торможения, которые не в состоянии сдвинуть орудие с места ни при каких из условий, встречающихся на практике.

Во всех существующих орудиях выстрел производится в тот момент, когда все части орудия находятся в покое. Вследствие этого отдача орудия выражается целиком в движении всего или части орудия назад. Если бы мы до выстрела сообщили орудию нек-рое количество движения вперед и произвели выстрел во время этого движения, то послед нее противодействовало бы отдаче и в зависимости от величины этого движения могло-бы поглотить всю или часть отдачи. По закону сохранения движения ц. т. системы тел, ц. т. ствола орудия и снаряда, находящихся в движении до выстрела, продолжает и во время выстрела двигаться с тою же скоростью и в том же направлении. Под влиянием давления овых газов ствол орудия и снаряда будет совершать некоторые относительные движения, скорости v и V которых определяются из уже известной нам формулы

(4>

Если движение ц. т. группы совершалось до выстрела со скоростью ±с, то абсолютная скорость движения ствола после выстрела будет v — (±е), абсолютная же скорость, снаряда V +(±с). Т. к. нас интересует лишь движение ц. т. группы вперед, то в этом случае зависимость абсолютных скоростей ствола и снаряда после выстрела выражается формулой:

v — с=w=V _ _с (6).

О. а. о. и в этом случае равна

_F0+^9p_{=(№ + c)}|_ _(7>

Энергия отдачи

n Gw2 [(Q + 1,9 I))V-G-C]2 _/оч

-^{и =} “2^-“ iFG "· ^(8>

Т. обр. абсолютное движение ствола орудия после выстрела определяется состоянием его-до выстрела. Если скорость с равна той скорости v, к-рую приобретает под влиянием отдачи ствол орудия, находящегося перед выстрелом в покое, то w=0, то есть ствол орудия немедленно после выстрела останавливается. Энергия отката ствола делается также равной нулю. Но в этом случае, для того чтобы придать стволу к моменту выстрела скорость с= v, необходимо приложить к орудию импульс, равный отдаче орудия, то есть накатывать ствол вперед силами, равными тем силам, которые прилагаются к обыкновенным орудиям для торможения отката. Сделав скорость с равною ¹1 _а1>, мы уменьшим энергию-отката в 4 раза. Заставляя эту энергию расходоваться на сжатие пружин или других эластичных приспособлений, способных придать стволу орудия в момент следующего выстрела снова почти ту же скорость с мы получим очень простой способ уменьшать энергию отката в 4 раза и возможность использовать эту энергию для того, чтобы при следующем выстреле ослаблять влияние его отдачи. Кроме того способ этот позволяет использовать всю энергию отдачи, которая расходуется обыкновенно бесполезно, для увеличения энергии снаряда. Действительно энергия снаряда (вместе с овым зарядом) равна для этого случая

«дрС + 3^!

Энергия снаряда в орудии, стреляющем, в спокойном состоянии, равна — -У -. Таким образом приращение этой энергии

0+1,92р/_т. 1)2

для нашего случая равно - + ₄ J >

так как

(Q + 1,9р) F=Gn,

то это приращение энергии снаряда равно

². 1,9р

29

<;г‘, Q + ι,9ρ

29 2 9

Величины второго и третьего слагаемых по сравнению с первым незначительны и м. б. поэтому отброшены. Т. о. приращение энергии снаряда равно для нашего случая энергии отдачи орудия, стреляющего в спокойном состоянии. В нашем примере (смотрите выше) скорость движения ствола орудия под влиянием отдачи

329

7,2 1.9-0,7 390

11,57 м/ск.

Если бы ствол орудия обладал в момент выстрела половиною этой скорости, то есть 5,785 м/ск, то энергия отката равнялась бы

390 5,785» 2-9,81

= 665,25

кгм.

Эластичное торможение энергии такой величины не представляет никаких затруднений даже при откатах ствола не длиннее 1 метров Силы торможения отката не в состоянии при этом не только приподнять орудие, но даже сдвинуть его с места при всех условиях, которые встречаются на практике. Впервые этот принцип противодействия отдаче движением ствола орудия проведен в 1891 г. немецким инженером К. Гауснером [*]. Идеи

Фигура 9.

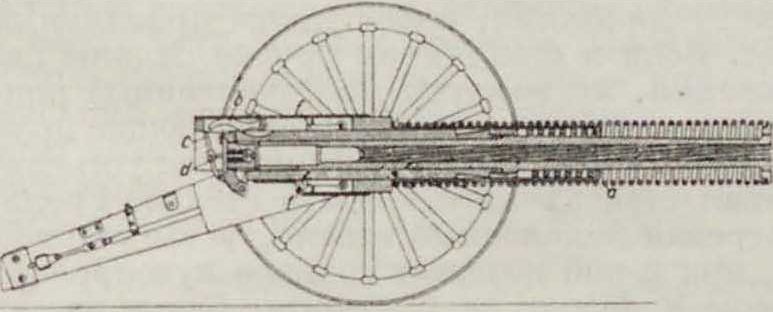
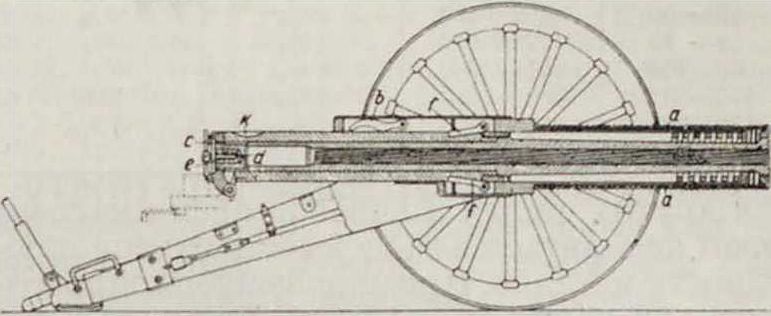
Гауснера не привлекли к себе никакого внимания. В 1905 г. швейцарец Р. Лак возвращается к этой идее [⁴], совершенно не сознавая ее значения. В 1906 году франц. правительство начало испытание горного орудия, построенного на этом принципе. Эдмунд Ре-гла (Edmund Royal а) дает кое-какие сведения об этом орудии и его теорию [⁵]. Образцом подобного орудия может служить полевое орудие, схематич. изображение которого представлено на фигуре 9 и 10 и конструкция которого патентована автору настоящей статьи в различных странах [·]. Ствол этого орудия движется под влиянием пружины а из положения, к-рое изображено на фигуре 9, в положение, изображенное на фигуре 10. Собачка Ь, прижимаемая пружиной к стволу, опускаясь вниз во время прохождения под ней углубления к на верху ствола, схватывает на короткое время рычаг с ударника d и оттягивает его в положение, изображенное на фигуре 9. Поднимаясь немедленно же после этого вверх, собачка b отпускает снова рычаг ударника и последний под влиянием пружины е ударяет в капсюль заряда. Происходит выстрел и при том в тот момент, когда пружина а придала стволу значительную скорость. Под влиянием давления поро ховых газов ствол быстро останавливается и получает импульс назад, достаточный для того, чтобы снова сжать пружину а и привести ствол в положение, изображенное на фигуре 10, где собачки /, прижимаемые пружинами к стволу, задерживают последний. После введения нового заряда в ник и приведения затвора в надлежащее состояние орудие готово для следующего выстрела, который и происходит в описанном порядке после того, как собачки b освободят ствол. Обозначая через: А—работу пружины этого орудия, S—работу трения и других сопро-

Фигура 10.

тивлений во время движения ствола вперед, Т—ту же работу во время движения ствола назад, V—скорость движения ствола вперед в момент непосредственно предшествовавший выстрелу, с—скорость движения ствола назад в момент окончания отдачи, F—величину отдачи орудия и М—массу ствола и движущихся вместе с ним частей орудия, мы получим три уравнения, позволяющие определить необходимую работу пружины:

F= М (г + с);

, Mi²

л-- -

S =

т.

Подстановкой в первое из этих ур-ий выражений для V и с путем дальнейших выкладок мы получим для А:

, _ F* м (τ+s) _ т-s

^Л ~ 8м ⁺ 2D* 2

Выведенное ур-не показывает зависимость работы пружины от величины сопротивлений Т я S и дает конструктору все необходимые указания относительно применения б. или м. сильных пружин в зависимости от сопротивлений Т и S, которые он может изменять в очень широких пределах. л Jlum.: >) Z e u η е г К., Technische Thermpdynamik,

2 АиП., В. I, Lpz., 1900; ²) W i 1 1 e R., Waffenlehre,

3 АиП., Berlin, 190ό; ²) г. П. 63146, Ан. II. 15353/1891:

«) Ши. И. 33598; *) R 0 g g 1 а Е., Ueber Geschiitze mit Kolirvorlauf, «Mitteilungen iiber Gegenstande des Artillerie-und Geniewesens», 1907, 8—9; в) Америк. II. 891778. Справочник по сухопутной поенной технике иностранных государств, М., 1928; Handbook of Artillery, Wsh., 1925; American Coast Artillery, Wsh., 1923. Л. Мартенс.