> Техника, страница 68 > Отражение света

Отражение света

Отражение света происходит на границе двух различных сред и неразрывно связано с преломлением света. Если показатели преломления (смотрите) обеих сред одинаковы, то О. с. не существует, хотя бы среды были совершенно различны по другим свойствам. Законы О. с. принимают простой вид для случая гладкой поверхности раздела, то есть такой поверхности, неровности и шероховатости которой малы в срав нении с длиной световой волны. При выполнении этого условия каждый луч падающего пучка света отражается так, что угол падения, образуемый лучом с нормалью к поверхности, равен углу отражения, причем оба луча, падающий и отраженный, лежат в одной плоскости с нормалью (закон О. с.). В случае шероховатой поверхности свет отражается неправильно (рассеивается во все стороны). Если же беспорядочные неровности поверхности немного превышают по размерам длину световой волны, то рассеяние света может быть интерпретировано, как дифракция световых волн. В случае крупных неровностей рассеяние объясняется, как О. с. от множества маленьких гладких поверхностей, наклоненных в различных направлениях. Дальнейшее изложение относится к правильному отражению от гладких поверхностей на границе изотропных тел.

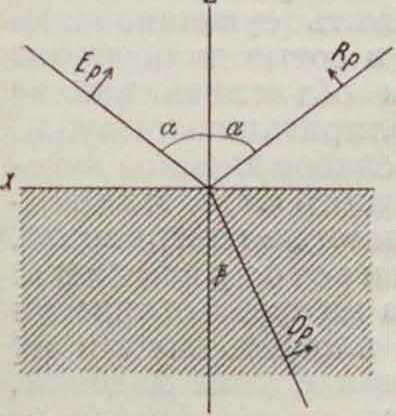
Основным свойством правильно отраженной волны является ее когерентность с волною падающей и преломленной; при встрече падающей и отраженной волны (фигура 1) происходит интерференция (смотрите). На этом основан метод получения когерентных лучей в различных интерферометрах (смотрите). На основании факта когерентности можно заключить с большой степенью точности, что частота световых колебаний при правильном О. с. от неподвижного зеркала не меняется. Наоборот, амплитуда и поляризация (смотрите) отраженной волны в общем случае совершенно иные, чем падающей. Следует различать три случая О. с. в изотропных средах: 1) О. с. от прозрачной, непоглощающей среды, 2) полное внутреннее О. с., 3) отражение от поглощающих сред, в частности от металлов. Во всех трех случаях направление отраженного луча определяется вышеуказанным законом О. с. В геометрии, оптике этот закон м. б. выведен из принципа Ферма

Фигура 1.

(смотрите Ферма принцип). Законы О. с., касающиеся интенсивности и поляризации отраженного света, очень сложны и совершенно различны в трех указанных случаях; они выводятся из общей теории отражения и преломления.

Теория отражения и преломления света впервые дана Френелем на основе представления о свете как волнах в упругой среде. С формальной стороны ур-ия Френеля полностью сохраняют свое значение в электромагнитной теории света. Пусть имеются 2 диэлектрика (смотрите), разделенные плоской поверхностью и характеризуемые диэлектрическими постоянными б! и ε₂ (фигура 2). На поверхность раздела под углом а в плоскости чертежа падает плоская поляризованная волна, разделяющаяся на отраженную (угол а) и преломленную (угол β). Таким образом факт отражения и преломления заранее предполагается. Для решения задачи о направлении, интенсивности и поляризации отраженной и преломленной волны нужно установить условия на границе раздела для электрич. и магнитных сил. Физически ясно,

что переход значения диэлектрич. постоянной из одной среды в другую не происходит математич. скачком, а протекает непрерывно, хотя и очень резко. Поэтому производные, входящие в уравнения Максвелла (см.

Максвелла ур-ия), сохраняют все время конечное значение. Отсюда следует,что и сами диференцируемые величины не претерпевают прерывного изменения при переходе из одной среды в другую. Если предположить граничный слой бесконечно тонким, тогда можно считать, что тангенциальные слагающие электрического и магнитного вектора не изменятся при переходе через такой граничный слой. Пусть ось Z совпадает с нормалью к поверхности, ось×лежит в плоскости чертежа, ось У перпендикулярна чертежу. Обозначим через

Ej-n E,jn Е_хг, Еу2, М_хi, Мух·, М_х2, Му

тангенциальные слагающие электрич. и магнитного вектора в первой и второй среде. Тогда граничные условия для тангенциальных слагающих выразятся так:

ли-ЙчГ-мГ } “^р"²-⁰· “>

V²

Из ур-ий Максвелла и условий (1) вытекают условия для нормальных слагающих

^ειΕ,ι=ε₂Κ_:11

Мл-М_л i

при Z= О

(2)

(магнитная проницаемость для световых волн положена равной 1). Разложим электрич. вектор падающей волны на слагающую в плоскости падения (фигура 2) и перпендикулярную к ней Е_я. Уравнение падающей •гармония. волны для оси×выразится так:

in г, „„ (. xsina + zcosai

Е_х=Ер cos a cos ω ^t — - _t. J,

где ω—угловая частота световых колебаний, полагаемая, в соответствии с опытом, одной и той же для падающей, отраженной и преломленной волны, νχ—скорость волны в первой среде. Для отраженной волны аналогично найдем:

R_x=Н_р cos a cos ω I i--_:---).

Для преломленной:

D_x=D_p cos β cos ω (i -,

где r₂—скорость волны во второй среде. Из (1) следует:

E_X+R_X~D_X

при г=0. Это условие должно удовлетворяться для любых хп t и следовательно аргумент последнего cos у всех трех ф-ий должен быть одинаковым, то есть

Sina _ SiOa Sin£

V χ Vi. V2

(3)

Ур-ия (3) равносильны известным законам отражения и преломления: а’—π—а

sina »ι „. > · W

гт—; ” —=Const

Siup V2 )

Для вьшода амплитуды отраженной и преломленной волны можно воспользоваться непосредственно граничными условиями (1) или комбинацией некоторых условий (1) и (2) и закона сохранения энергии. Энергия электрич. волны, падающей па границу раздела под углом a за 1 ск., пропорциональна е₁с₁Е² cos a, и соответственно для отраженной и преломленной волны—e₁c_lR²ccsa и е₂с₂П- cos β. Найдем сначала выражения для H_s и D_s. По закону сохранения энергии:

βχΟιΕΙ COS a=COS a + e₂c₂Dl cos β.

T. к. показатель преломления по электромагнитной теории света то имеем:

sin a _ Cl sin /ϊ ~ c₂

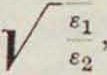
El COS a=R- cos a + _s^{sin n} D² cos β.

(5)

С другой стороны граничные условия (J) дают:

E_s + R_t=A,. (6)

Решая (5) и (6) относительно R_s и D_s, находим:

R,--E,

D.=b,

sin (a — β)

⁸ Sin (a+0) ’ 2sin/3 · cos a Sin (a -f- β)

(7)

(8)

Для расчета компонента Е электрич. вектора в плоскости падения воспользуемся граничными условиями (1) и (2).Из(1)имеем: Dy cos β= {Е_р- Ry) cos a. (9)

Из (2) соответственно:

Ry+Ey^D

Из (9) и (10) следует:

Sina

Р sin/i

(10)

Dy=E

- чб^-rei, 2 sin βcos a

P Sin(a + /J)cos(a-

(11)

(12)

Ур-ия (7), (8), (11) и (12) являются т. н. уравнениями Френеля, вполне отвечающими на вопросы об амплитуде, фазе и поляризации отраженного и преломленного света. Обозначим через L,_s, l_rs, 1_Λ, I._Ρ, irp> Eip интенсивности падающего, отраженного и преломленного света для колебаний электрического вектора, перпендикулярных и параллельных плоскости падения, и примем во внимание, что при преломлении сечение проходящего пучка расширяется; тогда из ур-ий Френеля получим:

т _ j Sin²(a-j5) j Sin2asin2/I.

^rs “ «sin»(a+ft»-^I*“-ⁱis 81п²(ДД7) _a3,

_{r r} tg -’(0-/5), _r J sin2asin 2β °

¹rr ¹‘P tg«(a+fl* “ ^Jfi>sin4a+/3)COS² (α-β)

В том случае когда падающий свет—естественный, то есть р и s компоненты некогерентны, интенсивность падающего света 1_е связана с интенсивностью отраженного и преломленного 1_Г и I_d ф-лами:

1е -Ifs “Ь Др 27_fS)

Ir “ -lrs + Irp j· (14)

™ Ids + lip

На фигуре 3 изображен ход отражательной способности ^rs и ^гр для вещества с показа-

¹ es ¹ ер телем преломления μ=1,50 для различных

15

Г. Э. т. XV.

углов падения. В предел!,ном случае отвесного падения естественного света из (13) и (14) следует:

г „te-JIS Ie l/+i; I

4, I (15)

Ie (e + lj- >

Состояние поляризации отраженного и преломленного света определится из уравнений Френеля, если составить отношение s и р компонентов. Для случая падения естественного света, когда Е_а=Е_р, из ур-ий (7), (8), (11) и (12) следует:

R_s _ cos(a-<3)

Rp ~ COS (α+β) ’

д — COS (a — β). и,

(16) (17)

Оба отношения всегда отличаются от 1, причем (16) всегда > 1 и (17) < 1, то есть отраженный и преломленный свет всегда частично поляризованы, но в обратных отношениях: отраженный луч поляризован в плоскости падения, преломленный — перпендикулярно последней. При a +

-M=f (16) обращается в бесконечность, то есть отраженный луч нацело поляризован в плоскости падения. Комбинируя условие a + β=" с законом преломления (4), получаем:

tga=/i, (18)

т. наз. закон Брюстера, определяющий угол полной поляризации при отражении. Поляризация при преломлении с другой стороны никогда не может быть полной. В предельном случае скользящего падения, когда α= ”, β по закону преломления

		j
	Irs	:
		//„е

ίο so so *о so so 70 < ’ У too node*ив в градус ал Фигура 3.

2 ’

определится условием следо вательно минимальное значение отношения (17) составит “. Если же падающий луч линейно поляризован, то отраженный луч, оставаясь линейно поляризованным, испытывает вращение плоскости поляризации. Если через φ обозначить угол, составляемый плоскостью поляризации с плоскостью падения, а через у тот же угол для отраженного луча, то по ур-ям Френеля

tgy =

COS (a 4- Д) COS (a - β)

(19)

Из ур-ия (7) следует, что знак R„ противоположен знаку Е„, с другой стороны, R_pтакже противоположно Е_р, что ясно из геометрических условий при отражении. Т. о. отраженная волна меняет фазу па 180° (потеря * при отражении). Законы Френеля неоднократно проверялись на опыте и могут считаться в основном вполне подтвержденными. Однако для многих веществ, и особенно твердых, при брюстеровском угле падения, удовлетворяющем (18), отраженный свет обнаруживает эллиптич. поляризацию вместо полной линейной, требуемой ур-иями Френеля. Это обстоятельство м. б. объяснено поверхностным переходным слоем конечной толщины, изменяющим граничные условия. Достаточно допустить существование такого слоя толщиною в сотые доли длины световой волны, чтобы объяснить вполне заметную эллиптич. поляризацию (Друде). Другой причиной м. б. слабое двойное лучепреломление поверхностного слоя, вызываемое молекулярными силами на поверхности.

Полное внутреннее отражение. При прохождении света из среды оптически более плотной в менее плотную по закону преломления (4), начиная с угла падения, определенного условием

sin a=μ, (20)

весь свет должен полностью отражаться. Основные положения теории Френеля д. б, применяемы и к этому случаю, т. к. граничные условия и предположение о неизменности частоты колебаний остаются теми же, то есть теория полного внутреннего отражения должна определяться ур-иями (7), (8), (11), (12). Математич. отличие заключается только в том, что амплитуды отраженного и преломленного света становятся комплексными. Подставляя вместо соя β в ур-ия (7), (8), (11), (12) на основании (4) значение можно привести ур-ия Френеля к нормальному комплексному виду. Комплексность амплитуд равносильна изменению фаз р и s компонентов отраженного света, и следовательно отраженный свет при полном внутреннем отражении вообще, говоря, должен быть эллиптически поляризованным. Для того случая когда падающий луч линейно поляризован в плоскости, образующей 45° с плоскостью падения, относительная разность фаз Δ отраженных sup компонентов может быть выражена на основании ур-ий Фрепеля ф-лой:

Δ COS О Esin- u-μΐ. ,₀

2 sill² a ’ (^1)

при a=” и sin a=μ (угол начала полного внутреннего отражения) Л=0, то есть отраженный луч поляризован линейно. Для угла падения а, удовлетворяющего следующему условию:

sin² α=

2/1=

1 + е²’

(22)

Δ достигает максимального значения Δ„_ηопределяемого равенством:

1-е³

2μ

(23)

Пользуясь полным внутренним отражением, можно т. о. превратить линейно поляризованный луч в эллиптически поляризованный, или при повторном или многократном полном внутреннем отражении—в луч поляризованный по кругу (смотрите Поляризационные приборы). Интенсивность отраженного света в случае полного внутреннего отражения получается в теории Френеля, как это ясно с самого начала, равной интенсивности падающей волны. Вместе с тем ур-ия Френеля приводят к результату, на первый взгляд парадоксальному, об одновременном существовании света и во второй среде, соответствующего преломленному. Действительно р и s компоненты для преломленного луча не обращаются в нуль для случая полного внутреннего отражения. Этот парадокс объясняется тем, что световая волна действительно заходит во вторую среду при полном внутреннем отражении, но снова возвращается в первую; так. обр. вся падающая энергия собирается в отраженном пучке. Графич. интерпретация ур-ий Френеля для полного внутреннего отражения дана Эйхен-вальдом. Для простоты на фигуре 4 выбран тот случай, когда полное внутреннее отражение "происходит при а=45°. Пунктиром изображены магнитные силовые линии (электрические силовые линии перпендикулярны к плоскости рисунка), сплошными линиями указано направление потока энергии, вектора Пойнтинга. Фигура 4 соответствует мгновенному положению; для получения кине-матич. картины нужно бы двигать чертеж в направлении оси У со скоростью света, деленной на sin а. Из фигура 4 видно, что ли-

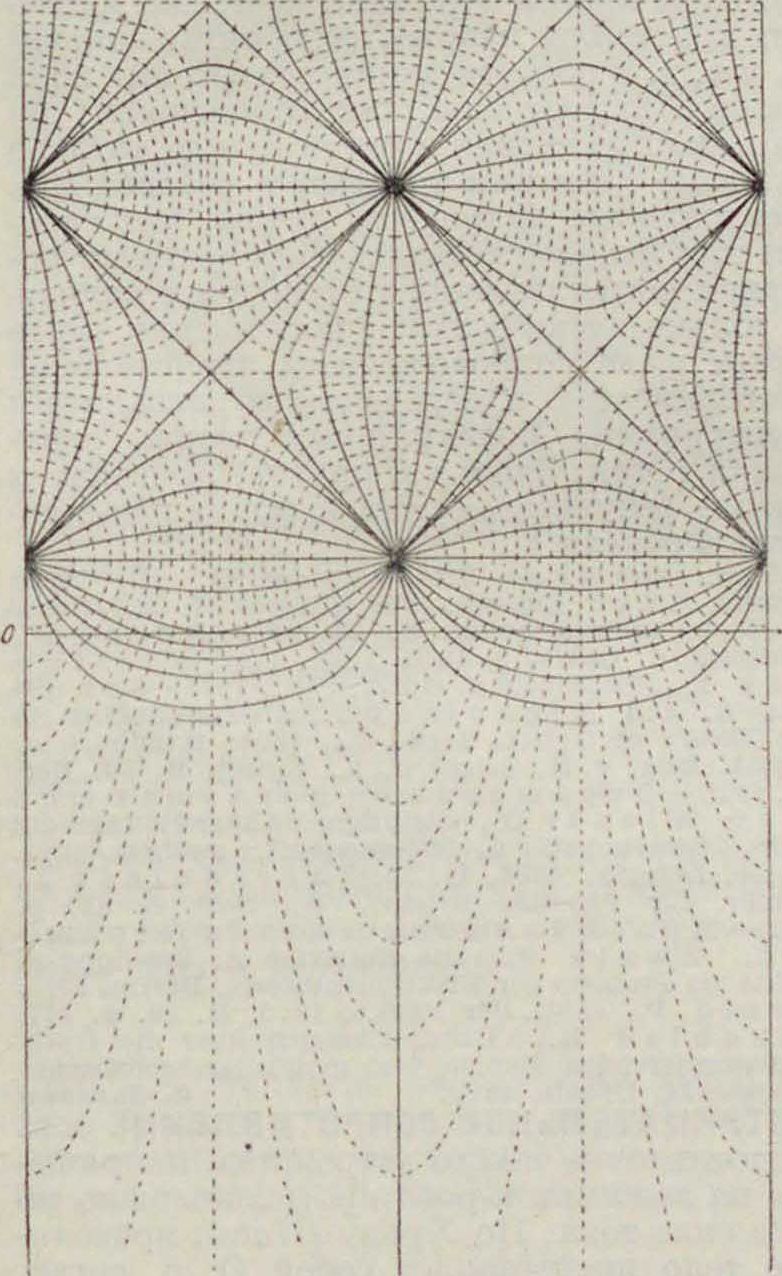
Фигура 4.

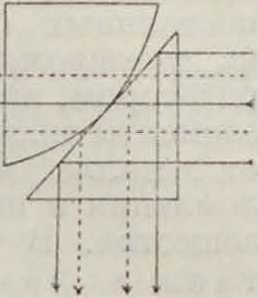
нии энергии заходят во вторую среду "и вповь возвращаются в первую. Волна во второй среде чрезвычайно быстро затухает, сосредоточиваясь практически в слое, соизмеримом с длиною световой волны, и распространяясь вдоль поверхности раздела. Экспериментально волна во второй среде при полном внутреннем отражении была обнаружена еще Ньютоном. Если привести в соприкосновение две призмы (фигура 5)— одну с плоской, другую с искривленной катетной гранью, то при падении лучей под углом полного внутреннего отражения свет проходит через вторую призму не только в области кон- -такта, но и там, где име- ~ ется воздушный зазор, соизмеримый с длиною световой волны. Вторая призма в этом опыте изменяет условия распространения волны во второй среде и «засасывает» ее в сторону (подобное возмущение связано, разумеется, с тем, что часть энергии ускользает из отраженной волны, и отражение, строго говоря, уже перестает быть полным).

Отражение от поглощающих сред. В электромагнитной теории света поглощающая среда характеризуется тем, что в уравнениях Максвелла наряду с током смещения учитывается ток проводимости и волновое ур-ие (например для компонента Электр ич. вектора X) принимает вид д²Х дХ

е^-Мжт^-еМХ, (24)

где о—проводимость. Вследствие поглощения волна в среде получается затухающей, причем в ней поверхность равных фаз в случае косого падения не совпадает с поверхностью равных амплитуд, что весьма осложняет характер явления. Взяв частное решение (24) вида

I 2я тх + пу + ρζ

Х=Ае ^{Г v},

где Т—период колебаний, m, η и р—в общем случае величины комплексные, v—скорость распространения волны, можно привести уравнение (24) формально к обычному виду волнового ур-ия, введя вместо ε комплексную диэлоктрич. постоянную ε

В

ε — ε— ϊΖσΤ.

этом случае ур-ие (24) примет вид е’ э“х. _νc*-w°^AX’

(25)

(26)

и формально теория Френеля автоматически переносится и на случай среды с поглощением. Так же как и при полном внутреннем отражении комплексность амплитуд в данном случае определяет эллиптичность поляризации отраженного света, то есть существование некоторой относительной разности фаз Δ между pus компонентами отраженного света. Обозначая через а угол падения, через у> т. и. азимут восстановленной поляризации, то есть азимут плоскости поляризации отраженного света (относительно плоскости падения) в том случае, если эллиптически поляризованный отраженный свет преобразован компенсатором (смотрите) в линёйнополяризованный, для чрезвычайно сильного поглощения (металлы) Друде получает следующие ф-лы для μ и к:

к — sin Δ tg^J у»,

μ=sin a tg a

COS2 V

i + cos δ sin 2 ν

(27)

(28)

Ф-лы (27) и (28) относятся к случаю падающего света, поляризованного под углом в 45° к плоскости падения. Формулы, связывающие μ и к с а, ψ и Δ, имеют большое практич. значение для определения оптич. постоянных (μ и к) металлов. Определяя на спектрометре (смотрите), снабженном поляризатором, анализатором и компенсатором, элементы эллиптичности света, отраженного от металла, можно найти показатель преломления и индекс поглощения изучаемого вещества. В табл. 1 приведены значения Таблица 1.—Значения μ и ft, для серебра для различных λ в А по Друде.

	/<	k
2 263	1,41	0,75
2 573	1,53	0,84
3 110	1,44	0,36
3 220	0,83	0,49
3 460	0,22	5,01
3 611	0,20	7.22
4 500	0,16	14,5
5 000	0,17	17,1
5 500	0,18	18,8
5 893	0,18	20,6

μ як для серебра для различных длин волн, выраженных в А, вычисленные по ф-лам Друде на основании измерений Минора. В табл. 2 приведены оптич. постоянные для

Га G л. 2.—О птические постоянные для различных металлов по Друде.

Металл	μ	ft
Висмут.	1,90	1,93
Свинец.	2,01	1,73
Ртуть.	1,73	2,87
Платина.	2,06	2,06
Золото.	0,366	7,71
Олово.	1,48	3,55
Серебро.	0,181	20,3
Цинк..	2,12	2,60
Медь..	0,641	4,09
Никель.	1,79	1,86
Сталь.	2,41	1,38
Алюминия.	1,44	3,63
Магний. 1	0,37	11,8

различных металлов по измерениям Друде, вычисленные по ф-лам (27) и (28).

Для отражательной способности поглощающей среды, то есть для отношения интенсивности отраженного света к интенсивности падающего в случае отвесного падения, ур-ия Френеля приводят к следующему выражению:

_ я-(1 + ft²) + 1 — 2μ

~ μΗί Г ft²) -г 1 +2/1

(29)

Отсюда следует, что для веществ с очень большим значением к и относительно малыми μ (металлы) коэф. отражения близок к 1 (металлическое отражение). Парадоксальное на первый взгляд поведение металлов, отражающих сильнее всего лучи наиболее поглощаемые, объясняется так же, как и при полном внутреннем отражении. Сильно поглощаемая волна заходит в металл на ничтожную глубину, соизмеренную с длиною волны, и затем почти полностью вновь поворачивает в первую среду, составляя отраженную волну. Чем больше поглощение, тем меньше глубина, на которую заходит волна во вторую среду.

Между оптич. постоянными вещества μ и к и его электрическими постоянными ε и о по теории Максвелла существует простое соотношение. Комплексная диэлектрич. постоянная (25) м. б. приравнена квадрату комплексного показателя преломления μ:

/t²= e-2iaT.

Для случая отвесного падения отсюда следует, что

μ²(1 — г/с)²=е — 2гстТ

или

/ζ²(1-Λ·²)=ε 1 ,„₀.

μ^^σΤΙ

Эти соотношения хорошо удовлетворяются для достаточно длинных волн (в десятки μ длиною) и неверны для коротких волн, что находит объяснение в теории дисперсии (смотрите) при учете наличия в среде резонаторов, определяющих зависимость ε и а от длины волны. Ф-лы (30) с качественной стороны объясняют особенность оптич. свойств металлов, устанавливая параллелизм проводимости и поглощения. Однако металлич. оптич. свойствами обладают и вещества, ничего общего с металлами не имеющие; густые растворы красок отражают свет, как металлы; кристаллы кварца, флюорита, сильвина и т. д. в области длинных световых волн также обладают металлич. отражением; пары металлов натрия и ртути при достаточно большом давлении отражают резонансные спектральные линии еще лучше, чем твердые или жидкие металлы. Необходимым условием металлического отражения является только очень большое поглощение, к-рое может и не сопровождаться значительной проводимостью и определяется связанными электронами. Молекулярная теория отражения (Озен, Эвальд и другие) приводит к тем же результатам, как и формальная теория Френеля.

Лит.: Общая:×Поль соя О. Д., Курс физики, т. 2 и 5, Берлин, 1923; Т а м м И. Е., Основы теории электричества, М.—Л., 1929; D г u d e Р., I.ehrbuch d. Optik, 3 Aufl., Lpz., 1912; Foretelling K., Lebrbuch d. Optik, Lpz., 1928: S c h и βίε r A. and Nicholson J., Ail Introduction to the Theory of Optics, 3 ed., L., 1924; Handbuch d. Physik, hrsg. v.H. Geiger u. K. Scheel, B. 20, Berlin, 1928.—О T p а ж e и и e от поглощающих сред; Wiener О., «Leipziger Abhandlungen der Sachs. Gesellschaft d. Wissenschaft, mathem,-phys. K lasse, Leipzig, 1908, II. 30; Z a h r a d n i ce k J., «Zlschr. fiir Physik», Brschw.—B., 1930, B. 65, p. 814. — Молекулярная теория отражения: E w а 1 d P., Die Reflexion u. Breehung d.

l.ichts ais Problem der Elektronentheorie, Berlin, 1925; E w a 1 d P., «Ann. der Phys.», 1916, B. 49, p. 117: Lundblad K., Untersuchungen iiber die Optik d. dispergierenden Medion vom molekulartheoretischen Standpunkt, Upsala, 1920. С. Вавилов.