 > Техника, страница 68 > Ошибки измерений и наблюдений
> Техника, страница 68 > Ошибки измерений и наблюдений
Ошибки измерений и наблюдений
Ошибки измерений и наблюдений,
объективные и субъективные ошибки, неизбежно сопровождающие как процесс измерений, так и процесс наблюдений.
Ошибки измерений (0.и.) Измеряя несколько раз одну и ту же величину со всей доступной нам тщательностью, мы в разных областях научного исследования, где применяются такие измерения (в астрономии, физике, химии, геодезии и прочие), получаем нек-рое, хотя и очень небольшое, расхождение результатов между собою. Так, при измерении при помощи микрометра несколько раз подряд одного и того лее расстояния между двумя намеченными точками, мы несомненно найдем, что полученные результаты не будут в точности одинаковы. Причины этого явления ясны: недостаточная отчетливость в отметке точек; при переходе от одного измерения к следующему небольшие измене-ния(напримерподвлиянием изменений 1°и влажности воздуха) как самого объекта измерения, так и той мерки, с помощью которой производилось измерение; субъективный отсчет, зависящий от мгновенного состояния измерителя и могущий допустить случайное отклонение в ту или в другую сторону. На конец ряд условий, связанных с различными видами наблюдения, вызывает эти колебания в результатах измерений. Принимают, что во всех таких случаях можно говорить о нек-ром «истинном» значении измеряемой величины; каждый отдельный результат измерения содержит «ошибку», которая равна разности между этим результатом и истинным значением измеряемой величины, причем это истинное значение в большинстве случаев неизвестно измеряющему. Вопрос о том, является ли принципиально допустимым во всех случаях говорить об истинном значении, есть вопрос теории познания. В качестве рабочей гипотезы это понятие оказывается весьма полезным.
Ошибки измерений различают систематические и случайные. Систематической называют ошибку, которая возникает под действием некоторой причины и потому сказывающуюся одинаково или приблизительно одинаково для всех повторных измерений. Сюда относятся ошибки, возникающие вследствие неправильного графления линейки, ошибочной конструкции весов и вообще всякой постоянной неправильности прибора, с помощью которого производится измерение. Сюда же надо отнести общие для всех ошибки, определяемые пространственными и временными условиями наблюдения или восприятия, в которых производится измерение (смотрите ниже ошибки наблюдения), и т. н. индивидуальные ошибки, то есть регулярные, всегда в одну и ту же сторону и приблизительно одинаковые по величине погрешности, имеющие своей причиной личные свойства измерителя или наблюдателя, связанные с несовершенством рецепторных органов человека. Эти систематич. О. и., свойственные данному способу измерения, должен быть изучены до начала измерений и затем или предупреждаются правильной организацией условий измерения или должны исключаться из каждого полученного результата. Способы определения этихсистемати-ческих ошибок для каждого прибора, а также и индивидуальных ошибок для каждого наблюдателя, равно как названных выше ошибок, вытекающих из общих психология, условий наблюдения, разумеется, различны для различных измерительных процессов. Случайными называются ошибки, причины которых не имеют постоянного характера, но меняются от измерения к измерению, так что и ошибки, вызываемые ими, от случая к случаю могут иметь разную величину и даже разный знак. Сюда в значительной мере относятся О. и., возникающие благодаря изменениям (°, силы и направления ветра, влажности воздуха и тому подобное., а также случайные погрешности субъективного отсчета, гл. обр. зависящего от психологич. фактора колебаний внимания.
Говоря об общей теории О. и., почти всегда имеют в виду только случайные ошибки, т. к. методы исключения систематич. ошибок зависят от данного прибора и не м. б. сколько-нибудь общими. Особенностью случайных О. и. является прежде всего то, что они м. б. исключаемы, в отличие от систематич. О. и., только после уже произведенных измерений. Основными задачами теории являются
следующие: 1) на основании произведенных измерений определить наивероятнейшее значение измеряемой величины и 2) оценить доброкачественность (надежность) полученного т. о. значения. Уже из этой постановки задач совершенно ясно, что они должны решаться методами теории вероятностей.
В основу теории, которая в главных чертах была разработана Гауссом, кладется задача: найти вероятность того, что ошибка окажется заключенной в данных пределах (о, Ь). Эта задача может быть решена различными способами; в основу каждого из них полагается та или иная гипотеза. Сам Гаусс выбрал за исходную точку постулат (требование), обычно называемый п р и н-ципом среднего арифметического: этот постулат состоит в том, что наивероятнейший вывод из системы равноточных измерений должен равняться среднему арифметическому полученных результатов". В настоящее время часто строят вывод на т. н. гипотезе элементарных ошибок, состоящей в том, что ошибка каждого измерения представляет собою сумму большого числа весьма малых ошибок, причины которых действуют независимо друг от друга. Примем ли мы в основание вывода ту или иную из этих двух гипотез, результат математич. анализа в обоих случаях оказывается одинаковым: вероятность того, что О. и. окажется заключенной между х и x + dx, где dx—малое положительное число,
равна h e~h‘x* dx отсюда следует, что ве-
Ул роятность попадания ошибки в конечный промежуток (а, Ь) равна ь
I h-e~hlx* dx. Это I *
и есть известная формула Гаусса. Здесь к означает положительное число, постоянное для данного типа измерений, но различное для различных типов измерений. Легко убедиться, что для измерений с большим значением h сколько-нибудь значительные по абсолютной величине ошибки становятся очень мало вероятными, что свидетельствует о надежности измерений. Напротив, если h мало, то относительно крупные ошибки могут сохранять еще довольно значительную долю вероятности, вследствие чего измерения являются мало надежными. Поэтому величину к обычно называют мерою точности данного типа измерений. Мера точности должен быть известна для того, чтобы можно было практически подойти к решению поставленных задач. Теория Гаусса позволяет из самих произведенных измерений найти наивероятнейшее значение h. Именно, если произведено п измерений и xlt хг. х„ ., х„ означают результаты этих измерений, а ξ среднее арифметическое этих чисел, то наивероятнейшее значение h равно
/="
1=1
Это число h, являясь показателем доброкачественности измерений, и решает собою поставленную задачу; однако часто бывает удобнее оценивать точность измерения другими показателями, которые все тесно связаны с h и м. б. вычислены, если h известно. Наиболее употребительны три следующих.
1) Вероятная ошибка—положительное число г, обладающее тем свойством, что вероятность быть меньше г для абсолютной величины ошибки равна в точности половине. Пользуясь приведенной выше формулой Гаусса, легко найти
0,478936 1 h
2) Средняя ошибка # —т. и. математическое ожидание абсолютной величины ошибки:
h f х1 e h*x*dx 2h fxe h2x2dx=- V-i V -i ·’ h у Л
3) Средняя квадратичная ошибка σ—квадратный корень из математического ожидания квадрата ошибки:
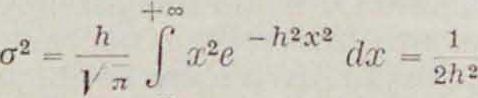
— 03
откуда
Р hV2
Все три показателя обратно пропорциональны к и отличаются друг от друга только постоянными множителями. Эти выражения ясно показывают, что величина h характеризует собою точность измерений.
Если имеется ряд неравноточных измерений, то для совместной их обработки удобно вводить т. н. веса отдельных измерений. Весом измерения называют величину, пропорциональную квадрату меры точности и по возможности выражающуюся целым числом. Если мы имеем ряд измерений, меры точности которых соответственно равны hu кг,., hn, а веса <7!, дг, ., д„, то Щ gji“, hi=дгкг, ., h%=gji2, где к—множитель пропорциональности; число h обыкновенно называют нормальной (вернее было бы нормированной)мерой точности. Смысл введения весов заключается в том, что единичное измерение веса д можно считать равносильным группе из д измерений веса 1. Поэтому, если все веса выражены целыми чи, всю имеющуюся систему измерений можно заменить для математич. обработки системой измерений веса 1. Этим задача обработки неравноточных измерений сводится к измерениям равноточным. Нормальная мера точности h очевидно есть мера точности каждого из тех равноточных измерений (веса 1), к которым мы сводим первоначальный ряд неравноточных измерений.
Нормальная мера точности к в сущности есть величина совершенно произвольная. Ее удобно брать малою, потому что тогда веса измерений становятся большими и с небольшою относительной погрешностью м. б. заменены целыми чи. Однако при слишком больших весах вычисления становятся затруднительными; поэтому практически следует в каждом отдельном случае доводить к лишь до такой степени малости, чтобы округление весов до целых чисел не вызывало" существенных искажений резуль татов. Не может существовать общего правила для этого выбора, в каждом отдельном случае приходится руководствоваться особым расчетом, к-рый при нек-ром навыке не вызывает больших затруднений.
Уже давно были замечены отдельные случаи, когда распределение ошибок значительно отклоняется от ф-лы Гаусса; в частности формула Гаусса дает симметричное распределение положительных и отрицательных О. и.; иногда на практике приходится встречаться с распределением, значительно отклоняющимся от симметрии; такое распределение не охватывается ф-лой Гаусса ни при каком значении параметра h. Иногда в таких случаях говорят, что ошибки не подчиняются теории вероятностей; это утверждение неправильно, потому что формула Гаусса выводится не из общих принципов теории вероятностей, а на основе специальных гипотез, как мы это видели выше; поэтому, если в каком-либо частном случае распределение О. и. не подчиняется закону Гаусса, то это может только означать, что гипотезы, лежащие в основе ф-лы Гаусса, в этом случае не выполнены. Различными авторами были предложены в большом числе другие законы распределения О. и., и некоторые из этих законов имеют опытное подтверждение; однако лишь весьма немногие из них по своей значимости выходят за пределы простых эмпирич. формул.
На практике часто приходится иметь дело со случаем, когда величины, которые нужно определить, недоступны непосредственному измерению, но мы можем измерить целый ряд ф-ий от этих величин. Тогда возникает вопрос о наилучшем возможном использовании полученных результатов измерений для определения искомых величин. В случае, когда число измерений превосходит число неизвестных, эта задача становится проблемой теории вероятностей. Метод, найденный Гауссом для ее решения и основанный на теории О. и., носит название способа наименьших квадратов.
Лит.: Лапан Л. К., Курс теории вероятностей, Москва, 1924; М и з e е 1, Вероятность и статистика, перевод с нем., стр. 174—183, М.—Л. 1930; СгиЬсг F. Wahrscheinlichkeitsreclinung. В. 1, Т. ?, Lpz.—В., 1908. А. Хинчин.
Ошибки наблюдений. Пользование самыми точными измерительными приборами в научном изучении различных явлений при простом и экспериментальном наблюдении и в разных видах технич. деятельности не гарантирует абсолютной точности измерения, поскольку агентом, производящим измерение, является всегда живой наблюдатель. Воспринимающий аппарат этого последнего не обладает абсолютным совершенством. Ошибки, которые допускает этот аппарат, определяются несовершенством его рецепторных органов, недостаточной их чувствительностью, своеобразными явлениями взаимодействия тех впечатлений, которые приходится воспринимать, а также психологическими условиями наблюдения при комплексной работе этих органов. Наконец в тех случаях, когда стоит задача регистрации и измерения наблюдаемого явления при помощи маниций с регистрирующими и измерительными аппаратами, входят в силу личные особенности движений наблюдателя. Тем более серьезное влияние ошибок на. непосредственное наблюдение, которое еще не поддается проверке при помощи точных приборов. Психологически изучена довольно обстоятельно прежде всего область рецепторной сферы, деятельность глаза, уха и др. органов чувств, которая прежде всего определяет наблюдение и в которой и появляются источники ошибок наблюдений. В специальной области т. и. психофизических исследований разрешалась задача определения чувствительности наших рецепторных органов к действующим на них раздражителям. Задача формулировалась какопределение порога чувствительности и обычно разрешалась в двух направлениях: 1) определения абсолютного порога, то есть минимальной величины раздражителя, которую способен замечать-данный воспринимающий орган—глаз, ухо и т. д., и 2) определения относительного порога, то есть того минимального-различия в раздражителях, к-рое эти органы в состоянии уловить. Для примера можно привести нек-рые данные, относящиеся к зрению и слуху. В области различения цветовых тонов максимальная чувствительность устанавливается по отношению к желтому и голубому, минимальная—по отношению к красному, фиолетовому и зеленому цвету. Кроме количественных различий в степени чувствительности здесь известны-случаи цветовой слепоты — неспособности различать некоторые виды цветов, встречающейся в общем довольно часто—от 3 до-6% всего мужского населения (смотрите Дальтонизм). Изменение силы освещения, например при переходе от дневного света к сумеркам, создает изменение в восприятии цветовых оттенков в отношении как их цветового тона, так особенно их светлоты (т. н. явление П у р к и н ь е); при полном дневном свете наиболее светлыми кажутся желтые цветовые тона, а в сумерки—зеленые и голубые, причем эти последние легко смешиваются в их цветовом качестве. Наконец в области цветового восприятия в смысле источника ошибок может действовать контраст одновременно или последовательно появляющихся цветовых раздражителей, в силу которого и светлота и цветовое качество изменяются (белый цвет на темном фоне кажется более светлым, красный цвет на зеленом фоне слегка изменяется в пурпуровый цвет, на желтом приобретает фиолетовый оттенок, в то яге время самый желтый фон получает зеленоватый налет и т. д.).
Целый ряд ошибок присущ зрению в области восприятия величины и расстояния предметов. Наиболее известными являются т. н. гео метрико-оптические иллю-з и и: заполненное расстояние кажется ббль-шим, нежели равное ему незаполненное; небольшие расстояния, заключенные между сторонами острых углов, переоцениваются в сравнении с большими расстояниями между сторонами тупых углов и т. д. Предметы различного цвета, находящиеся на одинаковом расстоянии от наблюдателя, кажутся одни более близкими (красные и желтые), а другие (синие и голубые) более далекими и тому подобное.
В области слухового восприятия ошибки в определении силы звука или высоты тона также зависят от степени чувствительности наблюдателя, с одной стороны, и от условий восприятшп—с другой. В средних высотах музыкальн.скалы нормально развитый средний слух может различать тона, отличающиеся на несколько колебаний в ск., а опытное ухо различает даже дробь колебания. Различна у разных наблюдателей чувствительность к интенсивности звука. В качестве общих условий, вызывающих здесь ошибки восприятия, нужно констатировать временные условия предъявления раздражителей, создающие контрастное взаимное влияние раздражений различной интенсивности: более сильный звук, предшествующий менее интенсивному, еще ослабляет этот последний для наблюдателя. Степень чувствительности воспринимающего аппарата индивидуально различна и в других областях, имеющих меньшее значение для научного наблюдения явлений,—в области обонятельного, осязательного в узком смысле слова, осязательно-двигательного, температурного, вкусового и т. д. восприятия. В качестве общего условия, вызывающего ошибки восприятия, здесь так же, как и в сфере зрения и слуха (являющихся основными средствами научного и прак-тическ. наблюдения), оказывается взаимное влияние одновременных и последовательных раздражений. Напр. отмеченный выше закон контраста—в смысле усиления одним раздражителем следующего за ним противоположного—действует и в области температурного восприятия (погружение нагретой или охлажденной руки в холодную или теплую воду) или вкусового (горький раздражитель, предшествующий сладкому, и. наоборот) и т. д.
Значение указанных выше источников ошибок в области собственно рецепторной сферы проявляется и должен быть учитываемо в сфере самых разнообразных сложных процессов научной итехн. деятельности. Ошибки в области цветового восприятия отражаются в ряде физич. наблюдений, в сфере цветовой и обонятельной, в области наблюдения химич. реакций, в области восприятия музыкальных тонов—в деятельности, оперирующей музыкальными инструментами, в области восприятия интенсивности и качества звуковых шумов, в области медицинских (аускультация и перкуссия) и технич. наблюдений, в области зрительно-пространственного восприятия в сфере геодезнч. и технич. измерений, в области цветового и пространственного восприятия в таких искусствах, как архитектура и живопись, в сфере чувств мускульного сопротивления— в некоторых областях технич. деятельности и т. д. В сфере наблюдения сложных явлений и процессов вступают в силу ошибки, проистекающие не от входящей в это наблю дение в качестве элементов деятельности собственно рецепторной сферы, а относящиеся к самому сложному акту наблюдения. Они зависят гл. обр. от деятельности внимания. При наблюдении неожиданно возникающих и быстро протекающих явлений может сказаться на неточности наблюдения недостаточная подготовленность внимания. При быстроте протекания процесса скажется ограниченность объёма внимания, не позволяющая в одном быстром акте схватывать большое количество зрительных или звуковых элементов. При длительно протекающих процессах обнаружится действие закона колебаний внимания, в силу которого последнее не может долго держаться на одной и той же высоте по отношению к однородным впечатлениям (общеизвестное явление—последовательного прекращения и возобновления тикания часов при долговременном слушании и тому подобное.). Дальше идет ряд ошибок т. н. ожидания, проистекающих от установки, определившейся в силу привычных ассоциаций: переоценка веса груза, имеющего ббльший размер, или медленно поднимаемой тяжести; или ошибки (в сторону преувеличения устанавливаемой величины) при уравнивании большей величины с меньшей и обратная ошибка при обратном отношении основной и подравниваемой к.ней. Такого рода ошибки лишь отчасти элиминируются применением измерительных приборов. Известные ошибки при субъективной оценке малых и больших промежутков времени устраняются применением хронометрия. приборов. Но часто нельзя устранить и ошибки объективной регистрации времени наступления или протекания явлений, связанные с применением хронометрии. приборов и зависящие от индивидуальных различий, восприятий, момента центральной переработки двигательных реакций. Повод к изучению этих последних дан был астрономическими наблюдениями, где было замечено, что различные наблюдатели давали различную регистрацию времени наступления одного и того же феномена, причем эта регистрация связана была с движением руки. Эта ошибка, называемая личной разницей или л и ч н ы м у р а-в н е н и е м и выражающаяся в нескольких сотых и тысячных долях ск., м. б. учтена путем установления типичного для· данного наблюдателя замедленного или быстрого течения его двигательных реакций. Кон-кротные количественные данные, относящиеся к вышеизложенному, см. Спр. ТЭ, т. I, стр. .116—121.
Лит.: Вундт В., Оспопанпп физиологии, психологии, пер. с нем., т. 2, гл. 10, 13, 14 и 15, т. 3, гл. 9, Москва, 1881; Holman n F. Rauinsinn des Auges, В. 1 и 2, Berlin, 1925; Luck lesh M., Visual Illusions, Their Causes, Characteristics a. Applications, New York, 1922; Mull e г 4. E., Die Gesichtspunkto u. die Tatsachen d. psycliophysischen Methodik, В. 1 и 2, В. 1904; С г u b e r. E., Theorie d. Beobachtungs-fehler, Lpz., 1911. В. Экземплярский.