Пара сил

Пара сил, или сокращенно, «пара», две равные по величине и противоположные ПО направлению силы, приложенные к одному и тому же телу. Плоскость, определяемая" линиями действия сил, составляющих пару (F. F), называется плоскостью действия пары, а расстояние d между этими линиями действия называется плечом пары. Силы, составляющие пару, определяют по отношению к какой-либо произвольной точке, лежащей в части плоскости, ограниченной линиями действия сил пары, нек-рую сторону враще-н и я пары .Моментом Н пары называется вектор, модуль которого М равен произведению F d=Fd и к-рый направлен перпендикулярно к плоскости действия

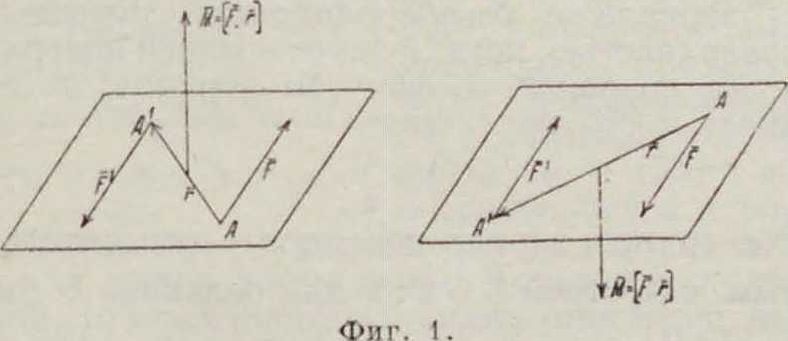
пары в такую сторону, чтобы он образовал вместе со стороною вращения пары право-вннтовую систему (фигура 1). Если А и A

суть точки приложения сил F и F и г А А ’, то не трудно усмотреть, что

ЛГ-iF-r]. (1)

Модуль М численно равен площади парал-лелограма, образованного векторами F и F. Пусть имеются две параллельные, неравные по величине силы Fy и Р₂, так что

Fy > F₂ (фигура 2) и пусть А_у и А₂ — точки приложения этих сил. Найдя равнодействующую 11 этих сил (смотрите Механика теоретическая), приложенную к точке А, имеем:

R^Fy-Ft		(2)
ЛЛо F i		(3)
АА F 2		(3)
ЛА% — AAj Fi~F‘2	R »	(4)
А Αχ Fz	F₂	(4)

откуда имеем:

А Ау=АуТ_г (5)

По мере приближения величины Fy к величине F₂ отрезок ААу увеличивается, а В— уменьшается. В пределе, когда Fy--- F₂,

			r
h			/:
	A, A		A	4
«2		1 *·/-/·,	r,
		f, i		r

Фигура 2. Фигура 3.

то есть когда обе силы составят пару, R=0 н, как видно из равенства (5), ААу=оо. Отсюда следует, что П. с. не имеет равнодействующей силы, или что П. с. имеет равнодействующую, равную нулю и удаленную в бесконечность.

Пусть имеется napa(F.F), точки приложения сил которой суть А и A (фигура 3). Разложив силу F на две составляющие Fy и F, с точками приложения А у и А, получим систему, состоящую из трех сил—F, 1< и F. Сложив затем силы F₂ и F’ в одну равнодействующую F[=F— F._z, получим новую пару (Fy, Fy), статически эквивалентную данной; это значит, что одновременное действие сил -Fy,- F(, противоположных силам последней пары (Fy, Fy), уничтожает действие первой пары (F, F).

Так как

F, _ Рг _ F-Fy AA’ АЛ] АЛу

AA’ А у + АА АуА‘

Отсюда имеем:

F-AJF^FyAyA, то есть модули моментов двух рассматриваемых статически эквивалентных пар равны между собой, а т. к. и стороны вращения этих пар одинаковы, то и моменты их равны. Нетрудно доказать это положение и для более общего случая, а именно: если две пары, произвольным образом расположенные в двух параллельных плоскостях, имеют равные моменты, то эти пары статически эквивалентны. Применяя правило параллело-грама сил, можно одновременное действие двух пар заменить действием одной единственной пары, называемой равнодействующей парой, причем момент последней пары равняется сумме (векторной) линейных моментов составляющих пар. По-

(<3)

(Ό

(8)

следовательным сложением можно получить равнодействующую пару для какого угодно числа пар составляющих. М. Серебренников.

Лит.: см. Механика теоретическая.