Параллaкc

Параллaкc, угол, под которым некоторое данное расстояние видно из данной точки. Так, если расстояние а между точками А и В видно из отдаленного пункта S (фигура 1) под углом е, то последний и называется параллаксом пункта S по отношению к а. При постоянном .4S (например AS=d) величина параллакса будет зависеть от угла А В AS; при AS=BS величина е Фигура 1. достигает своего максимума и определяется из следующего соотношения:

Если пункт S лежит на направлении АВ, то ε=0. Так как при вычислениях ε обычно не превышает 1°, то на практике вместо приведенного выше ур-ия пользуются ф-лой:

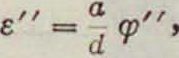
где д>=206 265. Таким обр. при сделанных допущениях величина П. обратно пропорциональна расстоянию. В астрономии под расстоянием а подразумевают либо радиус земного экватора (при вычислении расстояний внутри солнечной системы) либо средний радиус земной орбиты (равный ок. 23 400 земных радиусов), если вопрос касается расстояний неподвижных звезд от тел солнечной системы. В. Никаноров.

П. в астрономии различают суточный и годичный, причем суточным П. называется угол, под которым со светила виден радиус земли, проведенный в данную точку

земной поверхности, а также угол между направлениями на светило из данной точки и из центра земли. Наибольшей величины для данной точки П. достигает, когда светило видно в горизонте; соответствующий П. называется горизонтальным П. Наибольшую величину для земли вообще П. имеет в горизонте для точки земного экватора; соответствующий П. называется горизонтальным экваториальным П.; в дальнейшем он обозначен через п₀. Последний зависит только от расстояния А светила и связан с ним простым соотношением:

Δ — ^р— где у—радиус земного эквато-

ра. Для всех тел солнечной системы кроме луны (для которой средний π₀=57 2,70") можно по малости П. заменить είηπ₀ через л"₀ sin 1". Если еще за единицу расстояния принять большую полуось а земной орбиты,

то для А получается формула: А=> где в числителе стоит средний горизонтальный экваториальный Н. солнца. Имея в виду эту простую связь между расстоянием и П., эти два термина в современной астрономии принимают равнозначащими. Расстояния луны и солнца определяются именно посредством

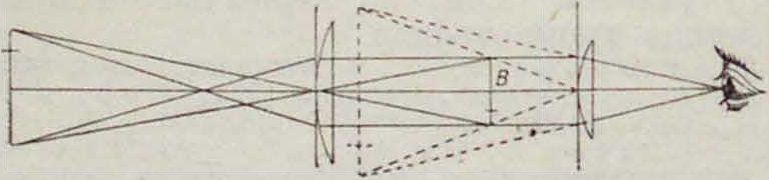
Фигура 2.

измерения ^ГП. либо путем наблюдения из двух разных точек земной поверхности, что дает разность соответствующих местных П., либо наблюдая из одного места, но пользуясь перемещением последнего вследствие суточного вращения земли (отсюда произошел и самый термин: суточный П.). В астрономических ежегодниках и таблицах положение тел солнечной системы всегда дается для центра земли (геоцентрические координа-т ы). Чтобы найти топоцентричес-к и е координаты, т.е. видимые из данного местаземной поверхности, нужно учесть влияние П., к-рый понижает светило к горизонту на угол ~~ sini·, являющийся П. по высоте. Здесь о есть местный радиус земли, z—зенитное расстояние. Влияние П. на

Фигура з. азимут ничтожно, т.к. происходит лишь благодаря отклонению формы земли от точного шара и ощутимо только для луны. П. по прямому восхождению а и склонению <5 вычисляется по ф-лам:

Аа — ^л°^е cos φ sin t sc <5;

At5=sin φ sin (γ — <5) cscy; tgy tg φ sc t,

где φ—геоцентрическая широта места. I—

часовой угол светила. Для луны эти выражения недостаточно строги и требуют еще дополнительных членов. Суточный П. для звезд исчезающе мал. По отношению к ним говорят о годичном П., то есть угле, под которым со звезды видна полуось земной орбиты. Связь годичного П. с расстоянием дается ф-лой А=^а -= — ,*!— а. Ближайшаязве-

зда имеет π=0,76", откуда А — 270 000 и. Для выражения таких больших расстоянии

Фигура 4.

употребляется особая единица, называемая парсеком (начальные слоги двух слов: параллакс, секунда); она равна 206 265 а·== 3,09 х10¹³»ш 3,26 световых лет. Тогда связь между П. и расстоянием становится еще проще: А=парсеков. Годичный П.

влияет на видимое положение звезды. Однако по малости его приходится учитывать только для немногих самых близких звезд. Для огромного большинства звезд он меньше 0,01". Иногда употребляется еще термин вековой II. Последний обозначает смещение звезды, вызываемое движением солнечной системы в пространстве.

Лит.: Иванов А., Курс сферич. астрономии, Берлин, 1923; de Ball L., Lehrlmch d. spharischen Astronomie, I.pz., 1912; EnzyklopUdie d. mathemati-pchen Wissenschaften, B. 6, T. 2, Leipzig, 1905—23; Valentiner V., llandwdrterbuch d. Astronomie. B. 3, T. i, Breslau, 1809. А. Михайлов.

П. нитей труб ы—кажущееся пере -мещение центра нитей трубы относительно точки визирования при перемещении глаза

1 гГ ЩШ

III

^С 1

^ь ^п~*· · ^зжммммжжт

шШш

Фигура 5.

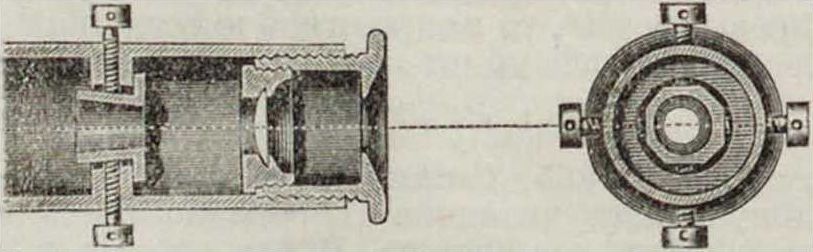
наблюдателя, вправо или влево, вверх или вниз относительно центра окуляра. Диафрагма с сеткою нитей устанавливается в трубе, в сеточном колене, в фокусе объектива, то есть в τολι месте, где получается действительное изображение предметов через объектив, рассматриваемое наблюдателем через окуляр (фигура 2—4): на фшг. 2—в точке В. При визировании трубою наводят на точку визирования центр пересечения двух нитей, или центр квадратика, образуемого четырьмя нитями, или-центр тр-ка,образуемоготре-мя нитями. При визировании нити должны представляться наблюдателю резкими линиями; поэтому перед наблюдением надо вдвинуть (или выдвинуть) окулярную трубочку bс из окулярного колена ВС настолько, чтобы нити представлялись резкими линиями (фигура 5). Затем при визировании на каждый предмет необходимо получать в трубе наиболее ясное его изображение; это достигается вдвижением (или выдвижением) всего окулярного колена ВС (вместе с трубочкой

be) в объективное колено DE с помощью зубчатого колеса и рейки (кремальеры). Однако точная установка сетки относительно действительного изображения предмета ви-

Фпг. 6.

Фигура 7.

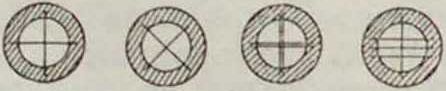
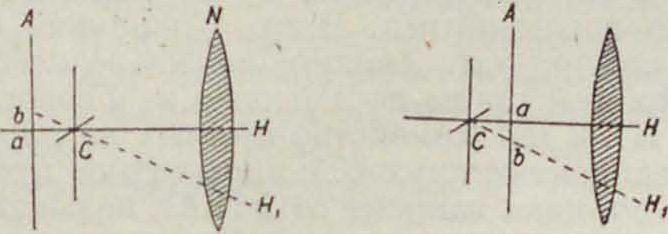
зирования не м. б. достигнута одною только ясностью видения изображения, потому что глаз не всегда улавливает при этом неточное совмещение плоскости сетки с плоскостью изображения в трубе. Между тем если сетка нитей не вполне совмещена с действительным изображением в трубе, то при различных положениях глаза наблюдателя центр нитей покрывает разные точки изображения, поэтому точное наведение не достигается. На фигуре 6—8, где С—плоскость сетки, А—действительное изображение, N— окуляр, Н—глаз, видно, что только при полном совмещении сетки С с изображением А точка изображения, лежащая против центра сетки, не зависит от положения глаза. Отсюда ясно, что при визировании, добившись ясности изображения предмета визирования и точки визирования, необходимо мелкими перемещениями глаза вправо, влево, вверх и вниз относительно центра окуляра убедиться в отсутствии П. нитей; если П. имеет место, то надо его уничтожить движением кремальеры, то есть сближением (или удалением) окуляра с объективом довести плоскость сетки до точного совпаде-

• ния с плоскостью изображения (фигура 8). Только при отсутствии П. нитей точность визирования трубою W равна точности визирования диоптрами (1), деленной на увеличение V трубы: W=* *.

Лит.: Соловьев С. М, Курс низшей геодезии, 3 И8Д., Москва, 1914; В и т к о в с к и и В. В., Топография, 3 изд., Μ., 1928; Б и к А. Н. и Чеботарев л. С., Учебник низшей геодезии. 9 изд., М.—Л., 1998. М. Бонч-Бруевич.