> Техника, страница 69 > Парусность

Парусность

Парусность, совокупность и система сшитых из полотнищ парусины мягких поверхностей—парусов, служащая д в и ж и-телем парусного судна, то есть аппаратом, воспринимающим и передающим корпусу судна силу ветра для приведения такого судна в движение. Паруса, рангоут и такелаж составляют парусное вооруэюенис (смотрите) судна. Система парусов зависит от типа парусного судна (смотрите).

В целях упрощения изучения теории II. полагают, что действие ветра на парусное вооружение, состоящее из ряда парусов площадью s,- с ц. т. их, расположенными в точках х₍, у(, может быть заменено равносильным действием ветра на теоретич. парус, площадь которого S=Ss< и ц. т. которого расположен в точке с координатами: х ~ Иг {S f. ΣS,·,

У - П/,5,·: Ss,·.

До последнего времени теория действия ветра на теоретический парус базировалась на исследованиях Ньютона, рассматривавшего это действие как совокупность параллельных ударов независимых друг от друга частиц воздуха о подветренную часть паруса. Это позволяло вести расчет практич. II. при помощи элементарных ф-л теоретич. механики и давало легкий переход от суммарной II. (теоретич. паруса) к отдельным парусам. Действие силы ветра согласно этой теории сводится к его давлению при нормальном направлении, равному

R~c-l_oSv

где γ—вес 1 м³ воздуха, g—ускорение силы тяжести, S—площадь всех парусов, v—относительная скорость ветра; коэф. с=2-^-4. Если ветер образует с поверхностью паруса угол а, то по этой теории R_a=R sin- и. Однако опытные исследования последнего времени показали, что коэф-т с =1,2 -т-1,4 и зависит от формы и отношения размеров паруса. Многолетняя практика парусного

1-Pacem до центра давления

t -Ширина паруса

НапР^а1

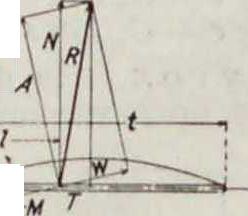
·.&- г флота указывает, что самый покрой паруса, зависящий от искусства мастера и дающий парусу при наполнении ветром определенную выпуклость (пузо), имеет большое знамение. Правильно сшитый парус хорошо наполняется и держит ветер, давая большой ход, в то время как плохо сшитый висит доской и при той же поверхности дает меньший ход. Всего этого приведенная формула не учитывает. Кроме того исследования показали, что R_a=R sina. Наконец центр давления ветра, то есть точка приложения его силы действия, совпадающая по теории Ньютона с центром парусности, в действительности меняет свое положение в зависимости от угла между направлением ветра и поверхностью паруса (угла встречи). Эти результаты привели к заключению, что отдельные частицы воздуха в своем движении связаны друг с другом, образуя струи, которые можно обнару-

Фигура 1.

Фиг. жить на некотором расстоянии от пару-са. 11арус,находясь в потоке воздуха, подвергается действию струй со всех сторон.

Обтекание ветром краев паруса, в oco-^nj-бенности при малых углах встречи, часто вызываетвихри, влиянием которых пренебрегать нельзя. Современные теории П., не отрицая значения главных аргументов, влияющих на силу действия ветра, установленных Ньютоном, вносят существенные коррективы в коэф-ты конечных формул, вывод которых базируется на ур-ии движения жидкости Эйлера и ур-ии давлений Бернулли. Однако результаты приложения этих ур-ий к совершенной и несжимаемой жидкости, дающие близкие к действительности результаты для перпендикулярной к плоскости паруса слагающей движущей силы, дают со-

Фпг. з. вершенно неверную величину для направленной по парусу слагающей силы сопротивления ветру. Последняя=О, т. к. в выводах не учи-"гг» тываются силы трения, которыми нельзя пренебрегать, в особенности в местах резкого изменения давления и скорости на поверхности и у кромок паруса, и которые вызывают вихревые движения воздуха, бесполезно поглощающие значительные количества энергии ветра. Т. к. кроме этого тео-ретич. выводы, давая общую картину явлений, страдают неточностями, зависящими от ряда допущений и условностей, вводимых при рассмотрении вопроса, то наиболее надежные основания для расчетов, как и в случае сопротивления воды, получаются путем обработки результатов испытания моделей в аэродинамич. трубе.

В целях сравнения между собой различных испытаний, результаты последних изображаются зависи мостями между величинами нулевого измерения, что делает их постоянными для любой модели и скорости при испытаниях. Если R есть результиру

ющая сила действия ветра на парус (фигура 1), то ее величина м.б.выражена ф-лой Ньютона:

Л-0_ri

ia

F v²

где С—уже переменный, эмпирически определяемый коэф-т, получаемый из опыта, a F—площадь (пластины паруса). Величина

Ta^v-4

называется подпорным давлением и в теории И. (пренебрегая изменениями у от давления и t° воздуха и беря значения у при нормальных условиях: 760 .им давления и 10^й) можно считать у=1,25 килограмм/м³; тогда

. v³

2-9,81 " ~ 16 ’

^П=й^Сг

F v³

Физич. коэф. С_г—давление ветра на парус площадью F=1 .и² при скорости ветра υ=4 м/ск определяется из опыта.

R=C_r· i] F.

Обычно определяют величины движущей силы А и силы сопротивления W, выражая их через коэф-ты С_а и С„:

A=C_a-q-F,

W=C_w - q · F.

Зная С_а и С„, можно найти R и угол этой силы с направлением ветра. Положение точки приложения силы R (центра давления) определяется из ур-ня .моментов (фигура 1)

М ·= N-1=C_mFq-t.

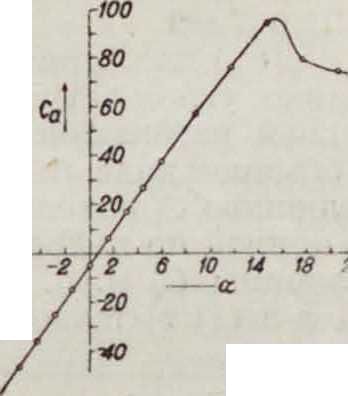
Коэф-ты C_r, С_а, C_w и С_т зависят: от угла встречи а, соотношения сторон паруса, его выпуклости и фор мы. Эти зависимости исследованы эмпирически (Croseck, Eiffel) для твердых пластин, имеющих размеры и форму паруса. Фигура 2 дает зависимость С₀= ·= /,(а) для симметрия. профиля каплеобраз-

*>· -i i »

Фигура 5.

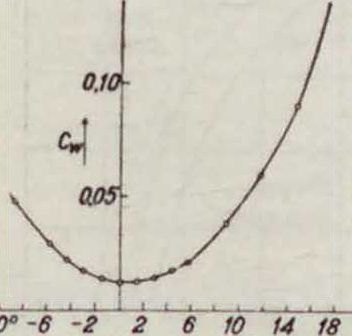
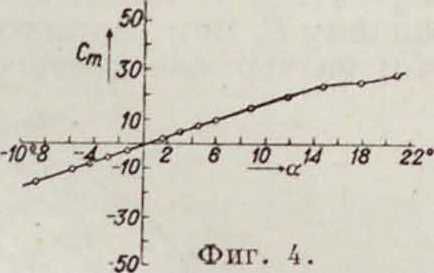
ной формы, полученную в результате аэродинамич. испытаний. На фигуре 3 дана функция С_№=/,(а), на фигуре 4—С_т=/₃(а) и на фигуре 5 —

I=/«(°). при этом

I __ C_mF f ^ Cm t C_nF · q Ca

Обычно результаты аэродинамич. измерений при испытаниях наносятся в форме С_а=φ(C_w), тогда каждой точке этой кривой (фигура 6) будет отвечать определенный угол встречи а, к-рый и обозначается при этой точке; при этом масштаб С,_г берется в 5 раз больше масштаба С„. Для использования в теории П. таких диаграмм их следует строить в одинаковом масштабе для С„ и С„. Тогда любая прямая, соединяющая точки кривой С_а=<р(С,_г) с началом координат, дает величину С_г при соответствующем угле встречи; на чертеже построено С_г для α= 14,4°.

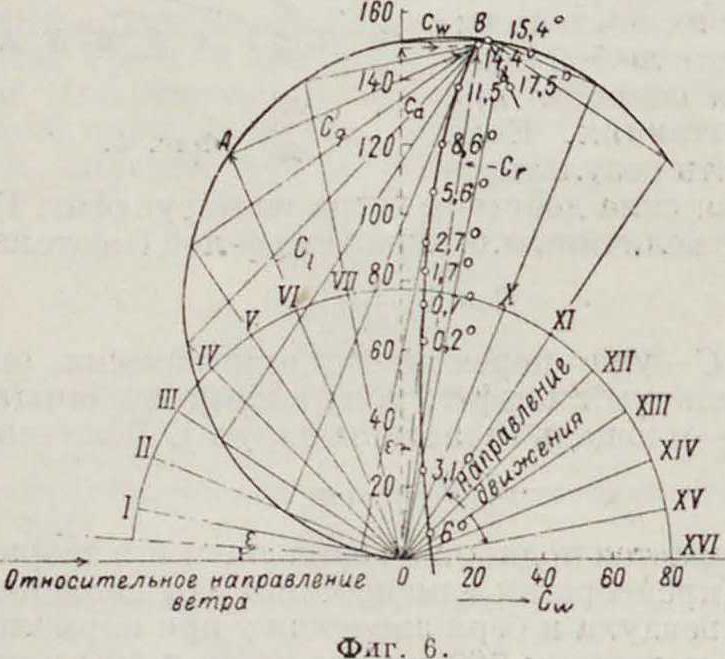
зволяют найти величины C₁, С_д и наивыгоднейший угол встречи. Так наир., для курса по VI румбу, проводя касательнуюАВ к кривой С_а=получаем C₁=О А и С_д=АВ,

α=14,4°. Аналитически:

@ι ·= С_а sin ε - С„ cos ε) _m

C_g=Ca COS ε + c„ sin ε ⁽

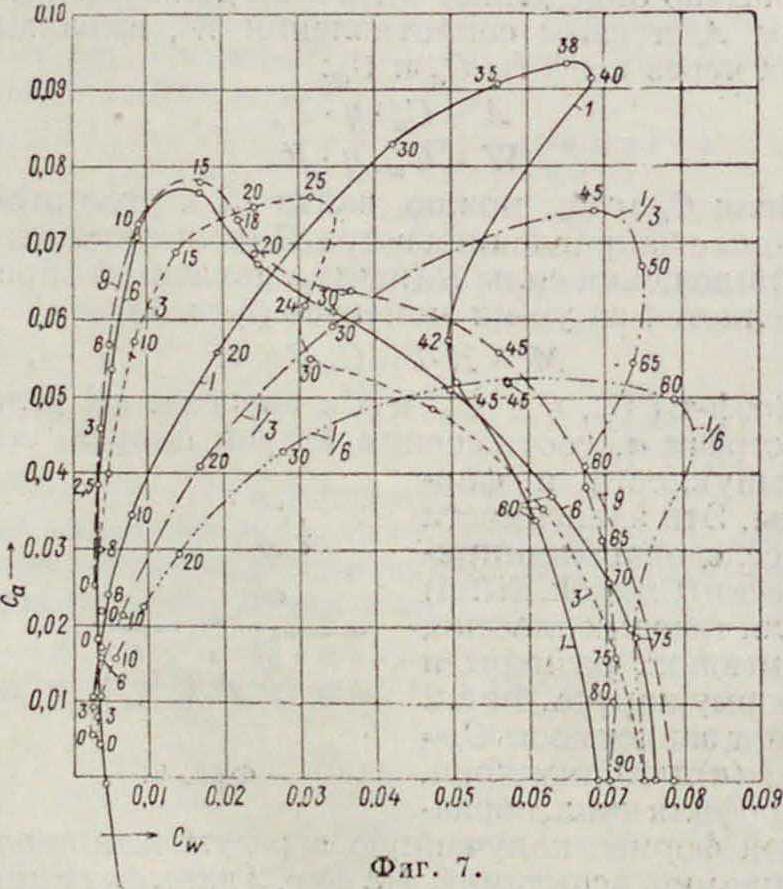
где e—курсовой угол. На фигуре 7 тонкой сплошной кривой представлена функция

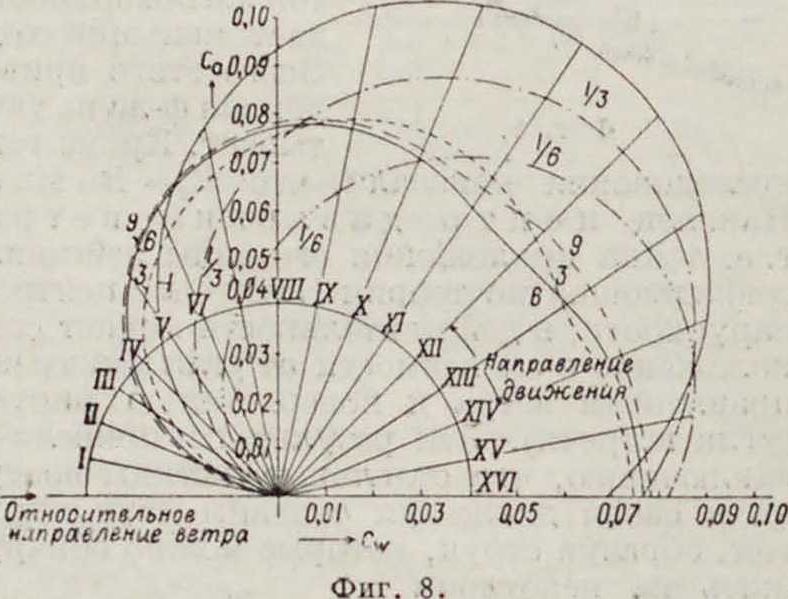
Весьма важно знать составляющие силы R по направлению движения судна и перпендикулярно к нему; обозначив соответствующие коэф-ты через -С_; и С_д, можно найти последние из диаграммы испытаний, построив геометрическое место оснований перпендикуляров, опущенных из точки О на касательные к кривой С_а=ср(С_1Г), то есть подножную кривую к последней. Так, на фигуре 6, проводя

касательную ВА к кривой в точке а= 14,4° и опуская на нее перпендикуляр О А, получаем точку А новой кривой ОАВ—к у р-совой диаграммы. Отрезки О А и АВ дадут величины С_г и С_д в масштабе диаграммы=С_а=φ(0,_Γ) для движения судна по VI румбу левого галса, считая румбы от направления ветра, к-рое на диаграмме принято постоянным. Точки курсовой диаграммы но-

С_а=<р(Ся>) Д^ля прямоугольной пластины при разных углах встречи, а на фигуре 8 такой же линией изображена курсовая диаграмма в ее обычном виде, без зависимости С_а=<р(С,_с). Величины Ci находятся как расстояния от О до кривой по направлению данного курса, а величины С_д м. б. получены аналитически. Из ф-л (1) вытекает, что при острых курсо-

фигура 9.

вых углах (е<90°) С_а должно быть большим, a C_w—малым для получения наибольшего Су, при полных курсах (е > 90°) величина C_t не уменьшается с увеличением С_м, а увеличивается. Т. к. C_w увеличивает дрейф и крен судна, то его в обоих случаях следует иметь минимальным. Т. о. величина С„ дает скорость судну, a C_w влияет на его крен и дрейф, что следует иметь в виду при изучении диаграмм C_a=<p(C_w).

Влияние отношения сторон паруса видно из фигура 7 и 8, где разным пунктиром обозначены диаграммы для отношения высоты паруса к его ширине: 9-|-^ι/«· Эти диаграммы показывают, что при близких к ветру курсах (до VI румба) наиболее выгодны высокие, узкие паруса (гафельные), при более полных(VI—XIVрумбы)—квадратные и при ветре в корму (XIV—XVI)—широкие низ

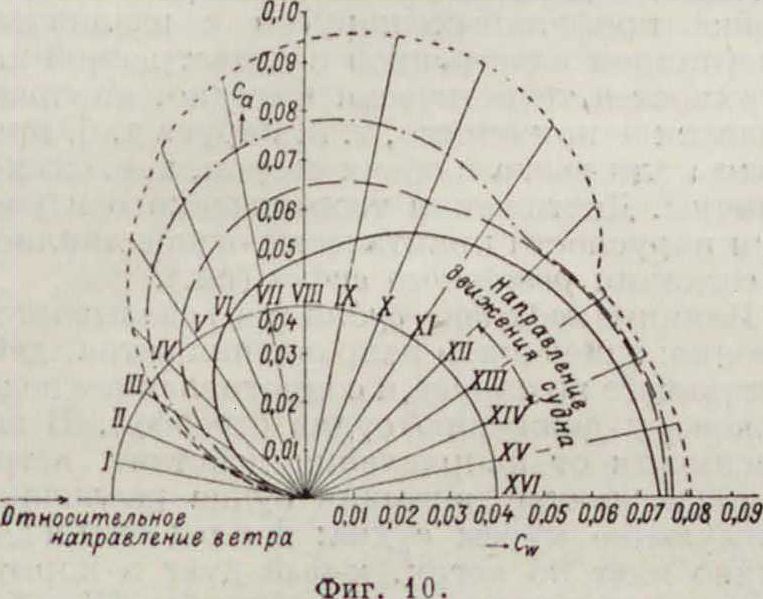
кие. Различный ход кривых объясняется различной величиной индуктивного сопротивления (смотрите); выделяя последнее, можно значительно уменьшить число экспериментов. Из фигура 8 вытекает теоретич. целесообразность применения многомачтовых шхун с вафельными парусами, имеющими на передних мачтах выше гафельных прямые паруса для полных курсов. Такое судно при соответствующем выборе поставленных парусов использует свою П. наиболее выгодно в зависимости от направления ветра.

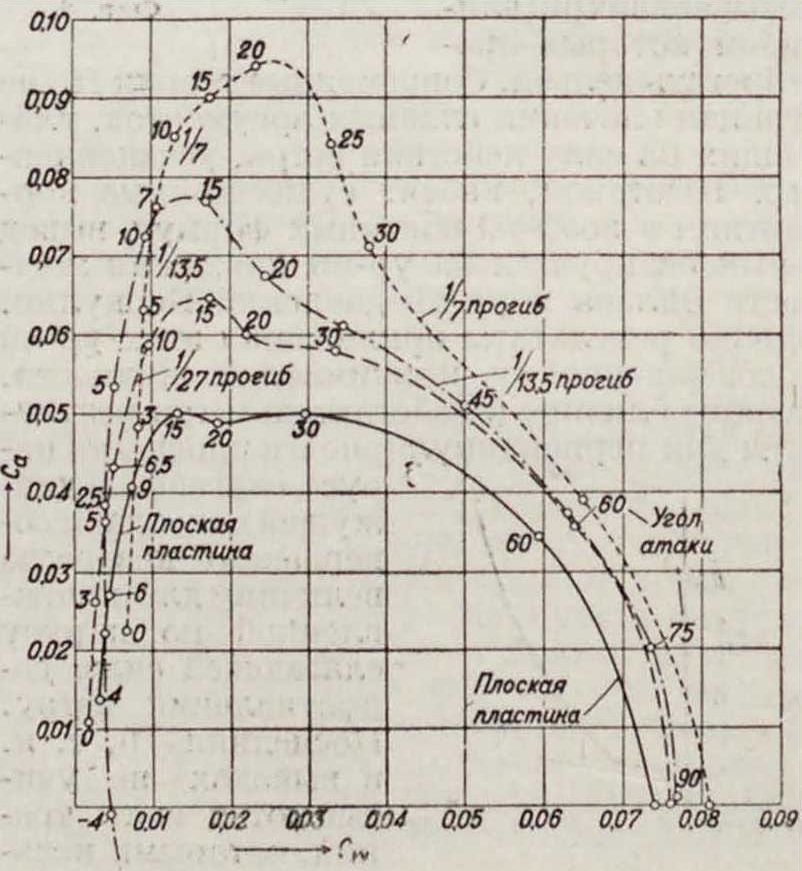
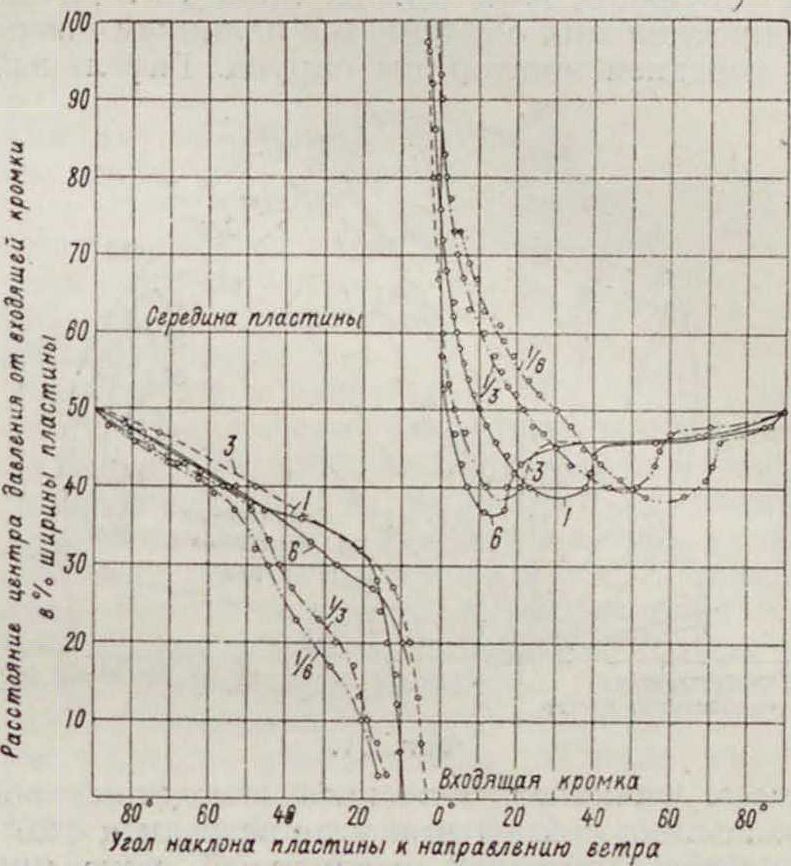
Влияние выпуклости паруса дано на фигуре 9 и 10 для стрел прогиба пластинки 0-т-¹/,. На основании теоретических и практич. данных в настоящее время предпочитают пузатый покрой паруса, между тем как недавно на гоночных яхтах ставились исключительно плоские паруса. Наиболее выгодная выпуклость не может быть определена из опытов над пластинами, т. к. мягкая поверхность паруса может иметь различную выпуклость в зависимости от направления ветра (угла встречи). Практически наиболее выгодна стрела прогиба что видно из диаграмм. Форма кривой пуза имеет второстепенное значение. Влияние контура паруса сказывается на величине индуктивного сопротивления. Узкая входящая шкаторина невыгодна при близких к ветру курсах и выгодна при полных, что является еще одним преимуществом гафельных парусов. Влияние контура паруса сравнительно ма ло изучено, и можно сказать только, что на полных курсах наиболее выгодна эллиптич. форма. Форма 2 (фигура 11) увеличивает индуктивное српротивление на 3—5%, формы 3, 4, 5 несколько меньше; форма 6 увеличивает его на 12%.· Прямые паруса относительно

Фигура 12.

выгодны (при полных курсах), паруса с острыми углами невыгодны, и у них эти углы следует закруглять. Положение центра давления показано для плоской прямоугольной пластины на фигуре 12 тонкой чертой; там же даны кривые для различного отношения сто-

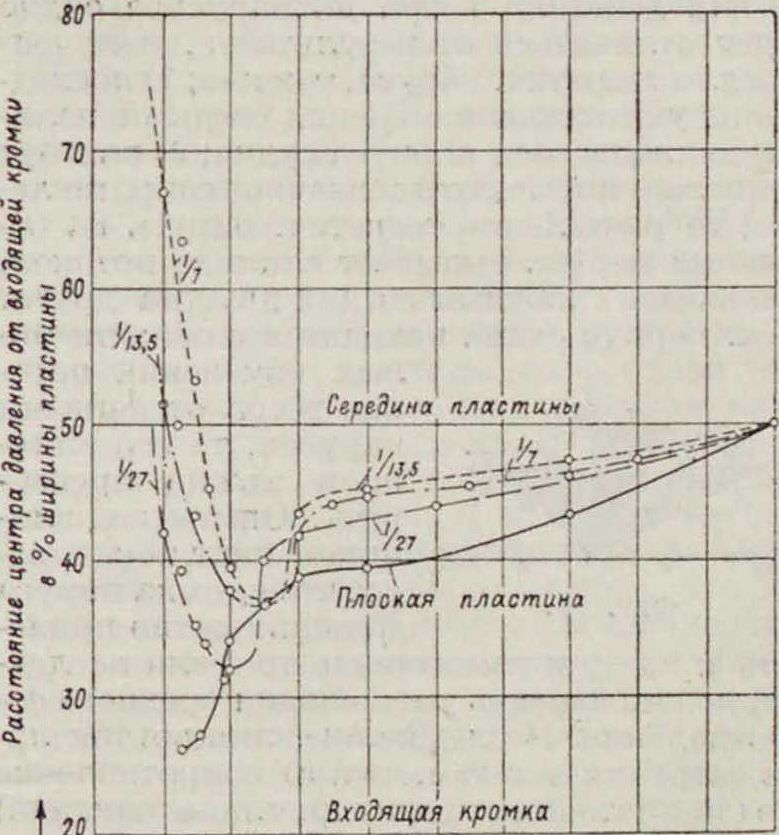
-ю о“ То го зо То м во То so so°

-► Угол наклона пластины к направлению ветра

Фигура 13.

рон; фигура 13 дает влияние пузатости паруса на положение центра давления.

Переход от результатов испытания моделей к действительным скоростям и размерам как существующих, так и проектируемых судов для расчета парусности достигается гооо

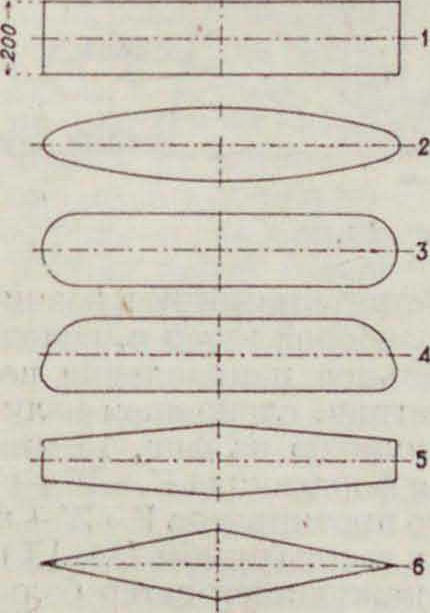
Фигура 11.

для струйного сопротивления при помощи закона аэродинамического подобия Рейнольдса (смотрите Аэродинамика).

На фигуре 14 приведены результаты испытания модели мягкого паруса, которые показывают близкое совпадение с испытанием соответствующих пластин. Нек-рое увеличение сопротивления объясняется наличием мачты у передней шкаторины паруса. Гафельный

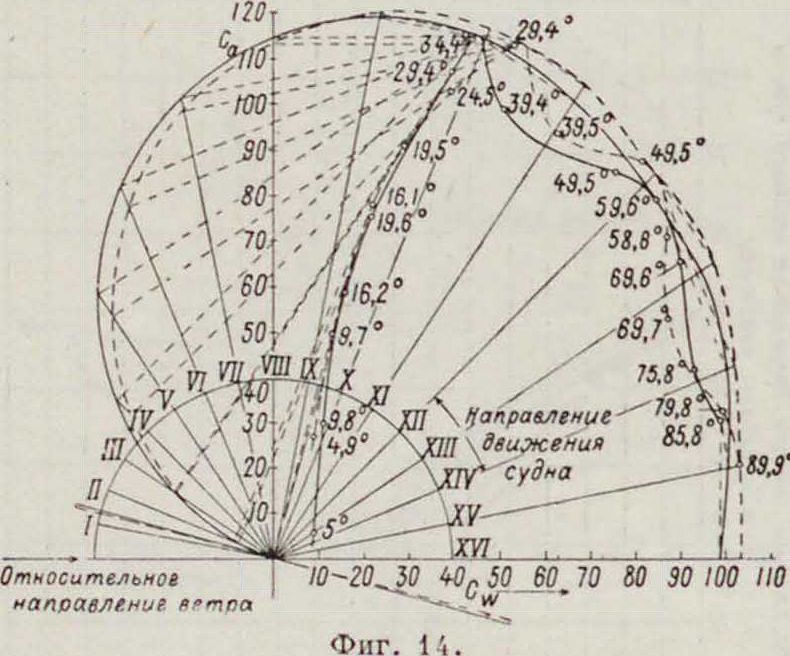
парус начинает полоскать вследствие образования вихрей при угле встречи а < 20°, а соответствующий квадратный даже при а < 30°. Для курсов до 10 румбов наиболее выгодно устанавливать гафельный парус под углом встречи а=25-р30° к направлению ветра, увеличивая его при более полных курсах до 90°. Практическое правило для установки парусов—углы между относительным направлением ветра и парусом и мелсду парусом и курсом судна должен быть равны.

Сила действия ветра на парусное судно будет отличаться от результатов, полученных для теоретич. паруса, так как: 1) последние не учитывают изменения среды от наличия движущегося корпуса судна; 2) рангоут и такелаж вызывают добавочное сопротивление; 3) разделение теоретич. паруса на отдельные паруса вызывает влияние потоков, обтекающих каждый из них друг на друга. Т. к. корпус судна находится в области малых изменений потоков ветра от наличия парусов, то его влиянием можно пренебречь. Опыты над влиянием мачт показывают, что кромка паруса должна плотно прилегать к мачте и изменением профиля последней можно достичь уменьшения вредного сопротивления. Исследование влияния такелажа затрудняется тем, что: а) сопротивление его (закругленных цилиндрич.поверхностей) в виду образования вихрей не следует закону подобия и в высокой степени зависит от числа Рейнольдса для действительного такелажа; б) форма такелажа не строго цилиндрическая; в) части его устанавливают на судне под разными углами к ветру. Опыты показывают, что сопротивление небольшого числа толстых снастей меньше, чем большого количества тонких. Влияние системы подразделения П. (типа парусного вооружения)

различно для разных курсов. На курсах, близких к ветру, опять сказывается преимущество гафельного вооружения перед прямым. Параллельные ряды парусов работают подобно би-, трипланам в аэропланных конструкциях. Особенно интересны случаи такого размещения парусов, когда между ними для прохода ветра образуется узкое пространство, играющее роль насадка и увеличивающее движущую силу паруса. Применение профильных парусов с различным очертанием наветренной и подветренной поверхностей теоретически выгодно, но практически неприменимо, т. к. паруса должен быть пригодны для ветра с обеих сторон, т. о. симметричны. Достижения теоретического изучения парусности практически осуществились в создании роторного судна (смотрите).

Влияние ходкости судна (смотрите) сказывается двояко: изменением направления ветра, действующего на паруса,и сопротивлением воды боковому движению судна (дрейфу). В зависимости от направления действит. ветра к направлению движения судна различают следующие курсы судна: ф ордевинд— судно идет по ветру, к-рый дует в корму, б а к ш т а г—ветер дует из румбов IX·—XV (сбоку сзади), г а л ф и н д, или полветра,— ветер дует из VIII румба (сбоку), б е и д е-в и н д—ветер дует из более острых румбов (сбоку спереди). При движении судно

Фяг. 16.

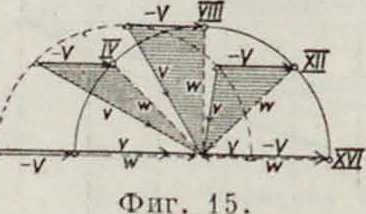
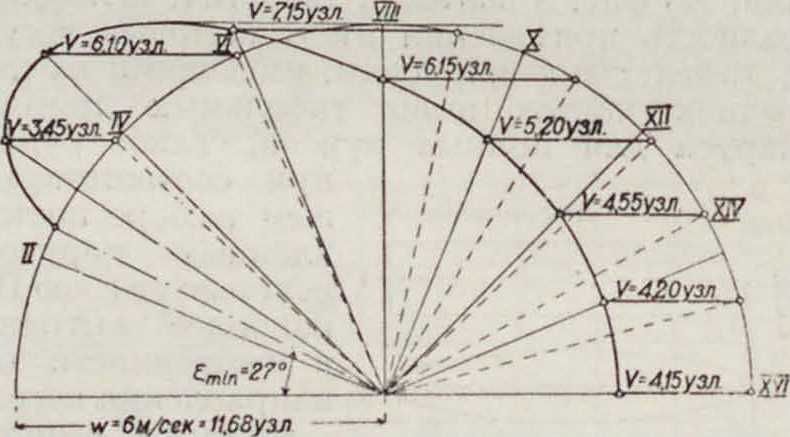
испытывает ветер действительный W и йозни-кающий от его хода лобовой ветер v, вследствие чего относительное направление ветра получается геометрия, сложением величин v и W, что выполнено на фигуре 15 при условии №=Const. Для фордевинда V --= W—v; для парохода, идущего против ветра V— W +ю. На курсах, близких к ветру (румбы II—IX), действующий на II. кажущийся ветер больше, а на полных курсах (румбы X—XIV) он меньше действительного W. Кроме того кажущийся ветер составляет с курсом корабля более острый угол, чем действительный. Т. о. судно по мере увеличения скорости подвергается действию ветра, заходящего к тсу. Фигура 15 отличается от предыдущей тем. что на ней направление движения судна постоянно, а ветра переменно, тогда как на курсовых диаграммах наоборот. Ii действительности скорость судна различна в зависимости от курса, поэтому пунктирный круг фигура 15 превращается в кривую, показанную жирно на фигуре 1G. Из последней видно, что наименьший угол между ветром и курсом ε =· 27°; обычно в зависимости от вооружения он лежит между IV и VI румба-

ми. При необходимости движения но курсу е < ^emin судно должно лавировать, т. с. ит-ти переменными галсами под углом ε > e_min(зигзагами). Наивыгоднейший угол лавиров-ки получают из полярной диаграммы фигура 17, где по румбам отложена относит, скорость судна; крайняя касательная к кривой дает направление наивыгоднейшего (для приближения к цели) курса; на фигуре 17 ε₀=52°.

Учитывая действие кажущегося ветра на паруса, рангоут, такелаж и подводный корпус судна, можно представить это действие замененным одной результирующей силой, приложенной в центре давления. Эта сила, вызывая движение судна, возбуждает реакцию сопротивления воды подводной части ч

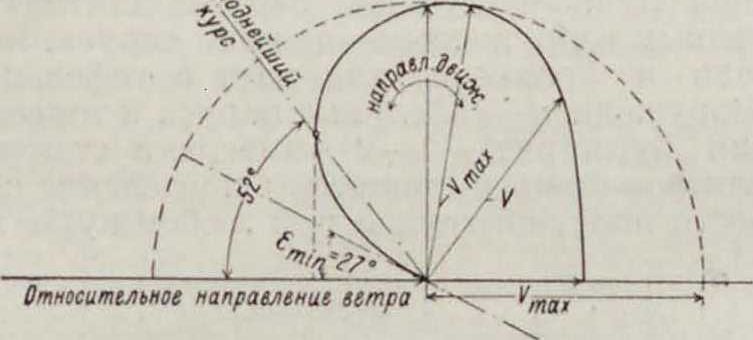
Фигура 17.

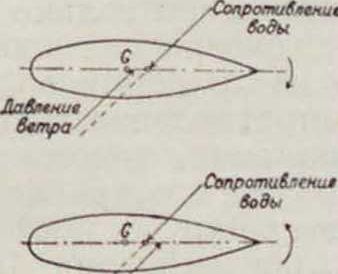
судна, приложенного в центре сопротивления. Силы давления ветра и сопротивления воды должны лежать в одной вертикальной плоскости (фигура 18, верхний чертеж), в противном случае судно будет или отходить от ветра (нижняя схема) или приводиться к ветру (средняя схема). В обоих случаях судно не будет держаться на курсе, причем вто- _х ^ΓοΈ^4,"^!"

рой случай не допу- —_Λ -

стим, т. к. если суд- ^фг- ^

но имеет свойство от-, лш.™.

Ottroa

ходить от ветра, то оно не способно к повороту через направление ветра (оверштаг), к-рый иногда необходим. Однако точный теоретическ. подсчет сил давления ветра и сопротивления воды и определение положения их точек приложения—

у/Давмни“

бетра

Фигура 18.

невозможны, т. к. помимо сложностей самого расчета положение центров переменно и различно при разных курсах в зависимости от угла встречи и крена судна. Задача конструктора сводится к огранич ίππο их перемещения, что легче достичь при гафельном вооружении. Поэтому производят так паз у с л о в н ы и расчет. Определяют положение центра П., к-рый принимают за центр давления, и ц. т. подводной части диаметральной плоскости — центр бокового сопротивления, к-рый принимают за точку приложения силы бокового сопротивления воды. II. проектируют так, чтобы центр ее был несколько впереди центра бокового сопротивления, т. к. последний при ходе корабля смещается несколько вперед. Это расстояние из опыта установлено сле дующим: для кораблей и шхун с прямыми парусамидз среднем 0,0G-P75L, для гафель-ных шхун в среднем 0,039L, где L—длина судна. Кроме того отношение момента площади передних парусов к моменту площади задних парусов относительно середины грузовой ватерлинии должно быть следующим: для судов с острыми обводами от 1 : 0,72 до 1 : 0,78; для коротких Широких судов от 1 : 0,76 до 1 : 0,82; для шхун с прямыми парусами от 1 : 0,82 до 1 : 0,92. При под- у счете в нок-рых слу- * чаях (яхты, крен судна) следует учитывать изменение скорости ветра в зависимости от высоты над уровнем моря. Если качества судна после постройки неудовлетворительны, то их можно исправить: 1) изменением П.—увеличивая или уменьшая передние или задние паруса; 2) изменением положения мачт—перестановкой или изменением наклона мачт; 3) изменением посадки судна — перемещением балласта или груза вперед или назад; 4) изменением формы корпуса—увеличением дейдвуда, укреплением новых досок, или уменьшением имеющегося (почти невозможно).

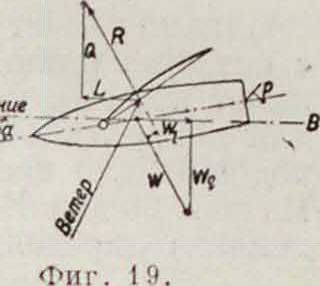
На фигуре 19 изображены силы, действующие на парусное судно на ходу. Давление ветра 11, как-указано выше, м. б. разложено на движущую силу L и силу сопротивления (ветра) Q. Обе вызывают движение судна; но т. к. сопротивление воды, также разлагаемое на составляющие W_t и W_q, в продольном направлении в 10 раз меньше, чем в поперечном, т. e. lEjsslOVK, то и движение судна получается вперед с нек-рым сносом (дрейфом) вбок по линии АВ, не совпадающей с диаметральной плоскостью судна, поэтому силы L и Wi следует брать в направлении движения судна, а не его диаметральной плоскости. В начале движения L > И⁷г, при установившемся движении и Q=W_g. Силы R и Wg практически не лежат в диаметральной плоскости и их приходится уравновешивать перекладкой руля (сила р). Силы L и W% не лежат также в одной горизонтальной плоскости, что вызывает незначительный диферент на корму, к-рый мы не рассматриваем. Силы Q и W_q помимо дрейфа вызывают крен судна, т. к. также расположены в разных вертикальных плоскостях; влияние крена настолько велико, что проблема П. тесно увязывается с остойчивостью, т. к. помимо уменьшения опасности опрокидывания меньший крен обусловливает меньшее сопротивление воды и больший ход судна. Из двух парусов, дающих одинаковую составляющую L, следует выбирать дающий меньшую составляющую Q, на что уже указывалось выше. Существует ряд эмпирич. зависимостей, определяющих полную площадь всех парусов S в зависимости от площади грузовой ватерлинии, миделя, диаметральной плоскости, смоченной поверхности и водоизмещения; последняя выражается

S:D*=k,

где к=1204-160 для кораблей, барков и бри-

гов; для яхт спортивных к=1804-~00. При необходимости увеличивать скорость судна новая П. определится из:

S,

А

S—.

v

Di ‘ ®* ’

где значки (_t) относятся к измененным заданиям; при том же водоизмещении Sj - &· t’J : г².

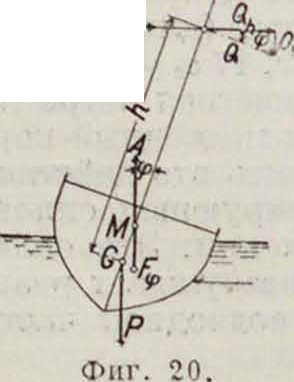
Однако расчет П. следует тесно связывать с остойчивостью. На ходу парусное судно имеет крен <р₀, к-рый не должен превышать: для кораблей 4°, барков и бригов 5°, пароходов 6°, для шхун, катеров 7° и яхт 84-10°. Из фигура 20 действительный угол крена (в радианах) определяется из Q h

^sin?=

где Р—сила тяжести и MG—метацентрическая высота, Q —кренящая сила. Л—ее плечо. Вводя площадь всех парусов S =kQ, получаем к sin φ=ε,

S It

p м a

где ε—эмпирическая величина; она равна: для рейсов в Индийском и других океанах 264-24, для Атлантич. океана 244-21, для европ. вод 214-Ю, для большого каботажа 194-17, для малого каботажа 174-14.

Величина ε наибольшая—для больших кораблей, меньшая—для шхун с прямыми парусами и еще меньшая—для шхун с гафель-ным вооружением. Для проверки условий остойчивости строят (фигура 21) диаграмму статич. моментов (смотрите Остойчивость судов) и кривую моментов силы ветра. При равном ветре от момента AD судно накренится на угол 18°, определяемый точкой F; при шквале: наибольший угол крена будет 37° и определится точкой Н, причем ADE=EGI1. Величина момента силы ветра, определяющая размер П., будет

М_тах - кМ,

где М=AD при угле AF не большем данной выше величины, а к =0,54-1,0 в зависимости от типа судна и условий его плавания. Определенная из условий остойчивости величина «S распределяется между мачтами в зависимости от типа судна (табл. 1).

Таблица 1.—Р асп редел сп не п л о щ а л и п между мачтами в процентном о т н

Размещение и размеры рангоута определяются величиной к" как входящим аргументом—отношением П. фок-мачты к S. Величина силы ветра и давления воды м. б. определена из испытания моделей судна в гидроканале и аэродинамич. трубе. Положение центров для условного расчета определяется чисто геометрически,причем учитывают в зависимости от

Направление ветра

io· его зо“ 40⁰ 50’ во· Фигура 21.

~*ψ90*

типа лишь следующие паруса: для мачт с полным вооружением—нижние паруса, марсели и брамсели, для мачт с гафельным вооружением—гафельные паруса и топсели, для бугшприта—1—2 кливера и стаксель или фор-стеньги-стаксель. Определение скорости парусного судна при любом курсе мо-

1

Г

—1

£

ίοΡ

0

L

Ϋ

V

N

J__1

ярусов S о ш е н и и.

Тип судна	Буг- шприт	Фок- мачта	Грот- мачта	Среди. мачта	Главк. мачта	КрюНс, или бизань-
						мачта
5-мачт, корабль.	6,24	Λ" 19,75	21,06	19,85	20,47	12,63
5-мачт, барк.	6.52	21,24	22,48	21,32	22,35	6.09
4-мачт, корабль.	6, СО	26.30	26.30		26,30	15.10
4-мачт, барк.	6,74	28,16	29.09	—	28,76	7,25
Корабль.	8.36	34,13	35.98	_		21,53
Барк..	9,27	32,28	39.58	:_	_	12,87
Шхуна-барк.	12,32	37,00	29,93	—	_	20 j 75
Бриг..	15.40	35,00	49,60	_
Шхуна-бриг.	16,04	47,20	36,76			_
Гопсельпая шхуна.	18.8ft	20,79	42,78	_		17,54
3-мачтовая ».	19,43	21,84	38,30	_	_	20,43
2-мачтовая ».	22.70	45.10	32,20	_
Гафельная ».	27,65	28,11	44,34	_
Люгер.		50,(9		_	_	18,14
Куттер.	31,00	69,00	—	— .·	• -ί~

Скорость ветра в м/сек Фигура 22.

жет быть в настоящее время теоретически определено только для идеального случая при следующих допущениях: сопротивление воды пропорционально г², дрейф равен 0, сопротивление воды не зависит от крена и волнения, действительный ветер постоянен по силе и направлению и не меняется по высоте; паруса поставлены наиболее рационально. На фигуре 16 и 17 представлены такие диаграммы для w=6 .и/ос. Эти диаграммы строятся для разного направления кажущегося ветра одинаковой силы, после чего делается переход к действит. ветру одинаковой силы для разных направлений. Скорость современных парусных судов приведена в таблице 2.

Как видим, наибольшая скорость достигается при курсе в полветра; падение ее при иных курсах происходит вследствие уменьшения С„. При уменьшении это правило нарушается, т. к. при более сильном ветре уменьшается парусность взятием рифов или уборкой верхних парусов. На фигуре 22 показаны кривые старостей для большого 4-мадтавого барка.

Таблица ^.-Скорость парусных судов.

---1- При силе ветра по Бофорту			2	3	4	5	в	7		9	10
	Длп курса		В среднем в					узлах
По	VI румбу.	1,3	3.1	4,7	6.3	6,7	7,6	7,8	_	_ I	_
»	ΎΊΙΙ ».	1,6	3,6	5,5	7.3	8.4	9,2	9.5	8.5	7,7	10
о	X ».	1.6	3.1	5,1	7,1	8,6	10,8	10,2	10,3	10,6	10
*	XII— XIV румбу.	1,5	3,5	5,9	6,7	8,8	9,7	10,3	11,1	12,5	11

Рассмотренные выше отношения С_а: С„характеризуют парусное судно с аэродинамической стороны, отношения V:охарактеризуют его гидродинамич. свойства. В виду ограничения условиями остойчивости последнее отношение на судах не м. б. повышено значительно. На буерах благодаря незначительному трению льда это отношение достигает 2,скорость доходит до 125 км/ч, и использование аэродинамич. возможностей П. достигает практич. предела.

Лит.: Мпддендорф Ф., Рангоут и такелаж судоп. пер. с нем. СИ К .1905; S с h w а г Т., Die Ent-wicklurig des Krb gssehiffbaues von Altrrtum bis zur Neuzeit. Lpz.,1909; Eiffel G., Der Luftwiderstandu. der Flue, B., i 912; Fu cbs II., Η о |) t I,., Aerody-naniik, B., 1 922; Flettner A., Die Anwendung d. Erkenntnisse d. Aerodvnamik zum Windantrieb von Schilfen. B., 1924^25; Flettner A., Meln Weg zum Retor, Epz., 1926; Betz A., Der Magnuseffekt d. Grundlage d. Flettnenvalze, <Z. d VDI», 1925, 3, p 1; Curry M., Die Aerodynamik des Segels, Diesseri vnr Mflnehen, 1925; Bader H., Beitrag zur Theorie des Segelns, Karlsruhe, 1925; Ackeret J., Das Kotorschiff u. seine physikalischen Grundiagen, 2 Aufl., Gdttingen, 1925. P. Тишбейн.