> Техника, страница 69 > Пары

Пары

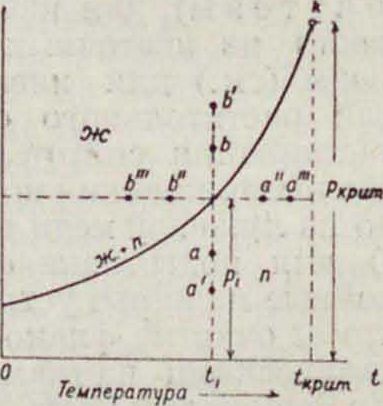
Пары, газы ниже их Г_крит. (смотрите Критические явления). Насыще н н ы e II. находятся в равновесии (смотрите Спр. ТЭ, т. V, стр. 352) с жидкостью или кристаллом, вообще с конденсированной фазой, из которой они образовались. Т. о. насыщенныйП. является одной из фаз двухфазной и однокомпонентной системы, что по правилу фаз (смотрите) отвечает моновариантности системы (одна степень свободы: f=N+2-P=1). Состояние насыщенного II., могущего существовать только в присутствии нек-рого количества конденсированной фазы, определяется поэтому только одним параметром, например 1°. При этом p=f (Т). Насыщенными м. б. II. только при 1° < Т_крит,. Ненасыще н-н ы е П. (перегретые; принципиально не отличаются от газов, приближаясь по свойствам к идеальным газам (смотрите) при повышении t° и понижении давления р; состояние ненасыщенных (чистых) П. определяется как и для любой однокомпонентной фазы двумя параметрами: <° и р. На фигуре 1 кривая р=/(<) есть кривая давления насыщенного пара;все точки [ ее представляют со- | бой состояния двух- ¹ фазн. моновариант- „ ных систем, которые | состоят из конден- 5 сированной фазы и II. Выше кривой— область конденсированной фазы ж; ее можно достичь например при i=Const, повышая давление (р > р в точках Ь,Ь) или при p=Const, понижая Г (t < t в точках b", b"). При обратных изменениях (при р<ср, в точках а, а или при t>t, в точках а", а") мы переходим в область перегретого П.—ниже кривой. Наибольшим давлением насыщенных П. является критическое давление, p“,_um., отвечающее наивысшей 1° сосуществования обеих фаз t°_Kpum.—критическая точка /с (смотрите Критические явления и Спр. ТЭ, т. V, стр. 403).

Термодинамика П. служит основанием всей современной теплотехники. Условие равновесия моновариантной системы, состоящей из т вес. ч. П. и (1— тонн) вес. ч. конденсированной фазы (жидкости) выразится ур-ием:

Vi-Vi-O, Vj-Vi. (О

где ip_г. Vi—термодинамич. потенциалы (у-= U -TS+pv) 1г пара и 1 г жидкости.

Ур-ие (1) связывает два параметра р и Т; будучи представлено в виде

Р-/СО, (2)

оно дает характеристич. ур-ие системы, или ур-ие кривой давления насыщенного П. При изменении 1° системы с Т до T + dT давление изменяется но ур-ию (2) с р до р -f dp; написав, что конечное состояние тоже является состоянием равновесия

Va + ФРα= Vi + ^Ψι

и сравнивая с (1), имеем: dy_а=А р_х, а т. к. dy> - - SdT + vdp, находим для (2):

гр dp

¹ dT

Q

Vi-Vi’

(3)

T. e. ур-ие Клапейрона-Клаузиуса, где Q—скрытая теплота испарения, v_t и v_x—удельные, или молярные, объёмы П. и жидкости. Когда г>! весьма мало сравнительно с v_%, то считая, что насыщенный П. следует идеальногазовым законам pv_t=RT (что справедливо для неплотных П., то есть при достаточно низких Т, например для П. ртути уже при обычных ί°), имеем вместо (3):

Цпр _. 9_. (Л)

dT IIт“ ^v

Интегралом (3) или (4) и является ур-ие (2); этот интеграл м. б. получен при различных допущениях о виде зависимостей Q=<p(T) и v_%— v,=A(T), ни одно из которых не является однако достаточно строгим и общим; например допуская, что ζ)=α-β_ιΤ+β_ίΤ²+., находим из (4) уравнение Дюпре-Гертца-Рен-кина-Нёрнста:

lgp=а- — с lgT + βΤ +. (5)

(дальнейшими членами β"Τ²+β"Τ* + ., как и βΤ, часто можно пренебречь). Пёрнет предложил простую приближенную ф-лу:

igp

^_T-+l,75 IgT- Т + С,

где <?„, E, С—постоянные, причем С—химия. константа, зависящая только от химич. природы П., но не фазы (1), могущей быть как жидкостью, так и кристаллом. Эти уравнения, хорошо удовлетворяя опыту в широком интервале Т, не дают, как и множество других б. или м. эмиирич. ф-л (например известная формула Реньо), обрыва кривой р=/(Т) в критич. точке (при t=t°_Kpum.) и вообще дают неправильные результаты при Т-* со, как показал Бачинский, давший эмпирич. формулы, удовлетворяющие этому условию.

Полная теплота сухого (т=1) насыщенного П.

(

L “ J Ci dT + Q=λ + Qi + р(гг — v_t) (6)

о есть количество тепла, потребное для превращения т=1 жидкости при <°=0° в ιοί

сьиценный пар при t°=<; λ c_xdT — τ e-

o

плота жидкости, а

Qi - Q - V (»,- Vi) -= (T g- p)(v_t-_Vl) (7)

внутренняя скрытая теплота испарения.

Для анализа вопросов технич. термодинамики П. весьма удобен графич. метод энтрной диаграммы. По оси абсцисс (фигура 2) откладываем энтропию S

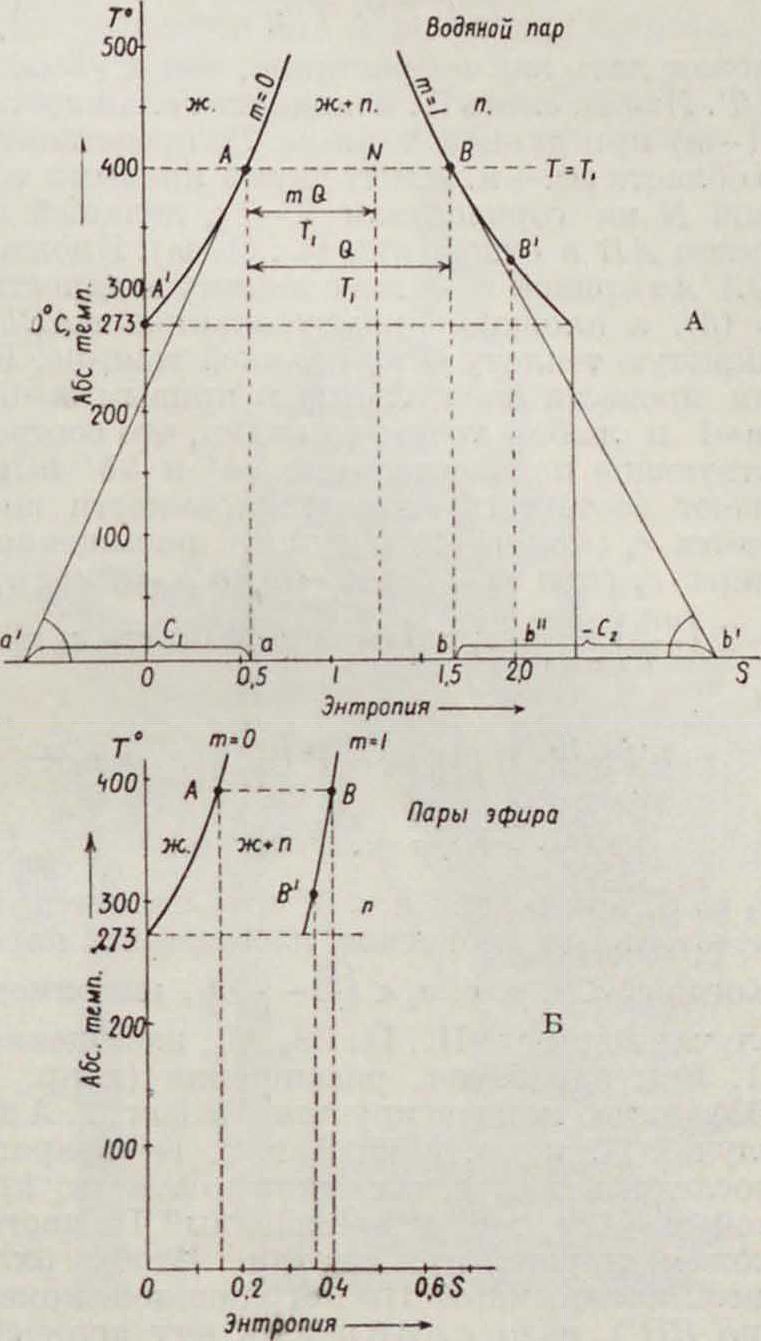
Фигура 2.

1 килограмм нашей системы, то есть в л а ж н о г о П., содержащей m кг II. +(1—т) кг жидкости в Са1/кг град., а по оси ординат Т° в абсолютной шкале;

^s-f+hf-}f··<*)

о о отсюда количество тепла, необходимое для бесконечно малого изменения состояния системы:

dq - Ci dT+ Td - [c_x + » (^ -

- dT + Q dm;

для сухого П. m=1 и dq - (с_х + ~ — dT, или

dq=c₂dr, (9)

где c_t=c₁ + ^dd?_Iг-®· Область влажного П.

на диаграмме заключена между двумя пограничными кривыми: т=0 (кривой жидкости) и 7П=1 (кривой сухого насыщенного П.). Ур-ие 1-й кривой

Т. Э. та. XV.

29

дает возрастание S с Т (фигура 2, А, Б). Кривая же 2-я (m= 1)

S-Si + I (11)

может дать как возрастание, так и убыль S с Т. Любая смесь II. и жидкости влажностью (Ι-m) при данной темп-ре Ί представится в области эю. +м. между двумя кривыми точкой N на горизонтали Т=Т_1г делящей отрезок АВ в отношении m : (1—m). Площадь О А Аа кривой т=0 дает теплоту жидкости λ в (6), а площадь прямоугольника аАВЬ— скрытую теплоту Q при данной темп-ре. Если провести касательные к кривым т=0 и т=1 в любой точке, то видно, что соответствующие подкасательные аа и bb выражают соответствующие теплоемкости жидкости C₁ (при т=0) и сухого насыщенного пара с₂ (при т — Const=1); aa=Tctga_x =

= Т _ - C₁ > 0 (можно считать c_t s с_р)

и

-b6- + Tctga_a-T(§)_m=rc₁ +

+ W-¥=^C>’ d²)

е₂ м. б. как >, так и < 0, что является замечательным свойством насыщенных паров.

Когда с₂ < 0, то есть с₂ < j, например в случае водяного Π., П. CS₂, 0₂, насыщенный П. при адиабатич. расширении (например по Вb) частью конденсируется. На фигуре 2, Адан случай П. воды, а на фигуре 2, Б—эфира; в последнем случае, как видно по наклону кривой m=1, е_г > 0, и насыщенный П. частью конденсируется при сжатии. Чтобы охладить насыщенный П. пограничной кривой (по ВВ), надо сообщить ему количест-т_х

во тепла f c₂dT (площ. bВВb") в случае т»

П. воды и отнять это же количество тепла в случае П. эфира (фигура 2). Для водяного П. Q=607,0—0,708ί (Клаузиус), L=

606,5+0,305/, Сг=§ψ - т=0,305 -

607-0,708! 273 + i

при:

1°. 0 40 100 160 200

с_г.-1,916 -1,538 -1,133 -0,832 -0,676

Для ряда углеводородов и их производных (Г„Н_в, СС1₄, СНС1») е₂=(Т) меняет знак, переходя через с₂=0 при некоторой Т°. По Матиа при Т° -*· Т_крит_, Q-* 0, J^-v-oo

(смотрите Критические явления), а поэтому с_гпри Т° -* Т_крит_ должно стремиться к пределу С₂=- оо.

ИсследованияРамзая-Ионга и Амага показали, что величина Т а следовательно и

(р - Т ||)=- к - Const (13)

одинаковы для П. различных веществ при одинаковых р. К приближенно равно м о-л е к у л я р н о м у (внутреннему) давлению П. (смотрите Газ, Капиллярные явления). Это условие (13) дает с ур-ием (4) для неплотных насыщенных П. правило Пикте-Трау-тона. С (13) связан закон Стефана-Баккера для внутренней скрытой теплоты испарения:

9а

Q - P(v а - %) - Qi=f К dv=a(^ - JJ;

последнее выражение справедливо, когда по Ваальсу К="_г. Из-за наличия поверхностного натяжения а давление насыщенного П. зависит от кривизны поверхности

*·; эта зависимость становится заметной при весьма малых радиусах кривизны (г<1/(). При этом: In—^:=~ к, где к=_D™_]{T (М—молекулярный вес; допускается, что pv=RT). При г>0 (радиус кривизны лежит в жидкости) в случае жидких капелек р_г > р; для Н₂0 при г=16 А р,.=2р; этим объясняются (Кельвин, Р. Гельмгольц) рост крупных капель туманов, росы за счет испарения мелких капель и задержки в конденсации п е-ресыщенных II. в отсутствии зародышей. В малых пузырьках газа внутри жидкости (г < 0) р,.< р, чем объясняются (Дю-гем) перегревы жидкостей выше t°_KU„. и конденсация П. в узких капиллярах (смачиваемых данной жидкостью), в пористых телах (например в адсорбенте силикат е-л е—скелете геля кремнекислоты); в несма-чиваемых жидкостью капиллярах она не конденсируется; там р_г > р. Электрич. заряд капли е понижает ее р_г и вместо гипербоды для In d получается кривая с максимумом

In

Рг _ i р κτϋχ

что объясняет конденсацию П. на ионах уже при малых пересыщениях. Влияние кривизны и электрич. зарядов на р стоит в связи с тем, что, как показал Н. II. Шиллер,р вообще возрастает при повышении внешнего добавочного давления Р (например давления индиферентного газа), и

In ^1,2 Pi

(Р

DiRT^{К 2}

Pi).

что выражает неприменимость закона Дальтона к насыщенным парам при высоких Р (смотрите Парциальное давление); в рассмотренных выше случаях Р₂ — Р_г=равно капиллярно му давлению.

Применение насыщенных и перегретых П. в тепловых двигателях общеизвестно. Свойства П. низкокипящих жидкостей крайне важны при coicuoicenuu газов (смотрите) и в холодильных машинах, а также и при использовании разностей /°, имеющихся в природе (например в тропиках разность /° воздуха и достаточно глубоководных слоев океана—Клод и др.). Высококипящие жидкости, например ртуть, м. б. применены в бинарных паровых машинах или турбинах и вообще в тепловых двигателях с несколькими рабочими телами (смотрите Бинарные машины). При этом возможно повысить наиболеее высокую /° рабочего цикла (7¹,) и тем повысить термодинамич. кпд η=-~^Т- ; в холодильнике тепло, отдаваемое высококипящей жидкостью, может идти на испарение низкокипящей жидкости (Н₂0, S0₂, NHj и др.), П. которой работают во 2-й машине; котел ее совмещен с конденса-

тором 1-й машины. Шребер предлагает последовательно соединять 3 машины со следующими рабочими телами: анилин (от ί°=310° до t°=190°), вода (от t°=190° до ί°=80°), этиламиы (от ί°=80° до <°=30°); термоди-намич. кпд такой машины ?;=33%. Наиболее выгодными рабочими П. являются согласно с энтрной диаграммой (фигура 2) те II., у к-рых отношение наибольшее. Наибольшее значение в технике имеют II. воды, углекислого газа, аммиака, сернистого газа и некоторых углеводородов. См. Спр. ТЭ, т. V, стр. 390, 399.

Лит.: ХвОЛЬСОН О. Д., Курс физики, т. 3, Берлин, 1923; Брандт Λ. А., Основании термодинамики, 4 иад. М.—П., 1923; Наумов В. С., Машиноведение, ч 1, М.—Л., 1928; Б ы к о в Н. А., Термодинамика, М,—Л., 1928; Гиббс В., Аэрозоли, пер. с англ. Л., 1929; Д у б б е л ь Г., Паровые машины и паровые турбины, пер. с нем., 2 изд., Л., 1 926; Янковский II. К., Паровые машины с двумя жидкостями (бинарные), Петербург, 1894; Не рнст В., Теоретич. и опытные основания нового теплового закона, пер. с нем., 2 изд.,М.—Л., 1 929; Clausius К., Abhandl. Uber die median. Warme-theorie, В. 1—2, 2 Aull., Brsch., 1876—1891; W i n-k e 1 in a η n A., liandbuch der Physik, B. 3, WSrme, Lpz., 1906; Schottky W., Π 1 i c li II. u. W a g-II e г C., Tliennodynanilk, B., 1929; Walther K. u. KOttinger M., Tecbnische Warmelehre; Nernst W., Orundlagen de3 neuen Warmesatzes, Stg., 1924; Schrfiter M. u. P r a n d t 1 L., Technische Ther-modynamik, Enzyklop. d. liiatheni. Wissensch., B. 5, Teil 1, 11. 2, l.pz., 1905; Scbu le W., Tecbnische Thermodynamlk, 4 АиП., B., 1923; Bryan G. H., Aligemeine Grundlegung d. Therinodynamik, Enzykl. d. math. Wissensch., B. 5, Teil 1, Η. 1, Lpz., 1903; Schreber K., Melirstofidampfinaschine, Lpz., 1902; J e 1 I i n e k K., Lehrb. d. pbysikal. Chemie, В. 1, 2 Aufi., Stuttgart, 1928; R a m say W. a. Young, «Philosophical Magazine», London, 1885, Series 5, v. 20, p. 515; «Journ. ol the Chem. Soc.», L., 1886, v. 49, p. 37—790; 11 о 1 b о r n u. Henning, «Wiedem Annalen d. Phys.“, Halle, 1908, Folge 4, B. 26, p. 833; Bertrand J., Tbermodynamique, Paris, 1887; Dubem P., Traiti <;16mentaire de micanique chi-mique fondic sur la tbermodynamique, v. 1—4, Paris, 1897—1899. П. Ребиндер.