> Техника, страница 70 > Переменные токи

Переменные токи

Переменные токи (переменные напряжения), изменяющиеся во времени токи (напряжения), проходящие попеременно то в одну, то в другую сторону. В русской терминологии нет четкого разграничения, и часто под П. т. понимают всякий ток, изменяющийся во времени, тогда как в ипостранной литературе alternating current, courant alternatif, Wechselstrom означают исключительно ток с чередующимся направлением, а изменяющийся вообще во времени ток называют courant variable, veranderlicher Strom и тому подобное. С этой точки зрения понятно выражение постоянный переменны и то к, то есть П.т., изменяющийся во времени по неизменному закону. Наиболее часто встречается на практике п е р и-одическийП. т., при котором все значения тока повторяются через определенный промежуток времени, называемый периодом. Число пер/ск. называется частотой тока. Между частотой и периодом существует соотношение:

/Г=1 или -, ·

П. т. получил чрезвычайно широкое распространение в технике. С одной стороны, передача энергии при помощи П. т. представляет в настоящее время то преимущество, что напряжение П. т. весьма просто преобразуется при помощи трансформаторов (смотрите); это дает возможность передавать на расстояние сотен км электрич. мощности в несколько сот тысяч kW. С другой стороны, при П. т. можно использовать преимущества коротко замкнутого асинхронного двигателя (смотрите Индукционные машины), являющегося во многих случаях незаменимой по простоте и прочности электрич. машиной. В технике связи П. т. применяются в самых разнообразных случаях, в радиотехнике для передачи сигналов, речи, для целей телемеханики, телевидения и тому подобное. Широкое применение П. т. в электротехнике привело к созданию целого ряда специальных приемов, ф-л и графиков, применяемых при решении задач П. т. и объединяемых в отдельную дисциплину под названием теории П. т.

Простейшим периодическим П. т. является синусоидальный ток, мгновенное значение которого г изменяется по закону синуса:

г=I sin (ωί + φ)=I sin [²* « + ?>]·

Здесь I—амплитуда колебания тока, со — круговая частота (пульсация), Т=²J —

период, φ—фазовый угол.

Синусоидальный П. т. (напряжение) возникает в прямоугольной рамке, вращающейся с постоянной угловой скоростью в равномерном магнитном поле (смотрите Генератор переменного тока). Для изображения синусоидального тока в прямоугольных координатах откладывают время по оси абсцисс, а силу тока по оси ординат (фигура 1). Фазовый угол зависит ог выбора начала отсчета времени. Данный ток опережает колебание г, равное I sin ωί, на

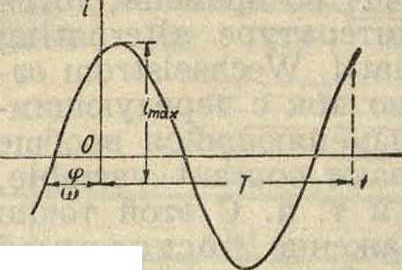
Фигура 1.

время Более удобным является выраже-

ω “

ние синусоидальных П. т. при помощи векторных диаграмм (смотрите), когда каждый ток рассматривается как проекция вектора, изображающего данное колебание, на равномерно вращающуюся ось времени. Длина этого вектора равняется амплитуде колебания, а угол с осью времени определяет фазовый угол колебания. При сложении нескольких синусоидальных колебаний одного и того же периода равнодействующее колебание является тоже синусоидальным и изображается при помощи суммы векторов, изображающих составляющие колебания. Если периоды составляемых колебаний несколько различны друг от друга, то результирующее колебание оказывается несинусоидальным и возникают биения (смотрите).

В нек-рых задачах требуется определить среднее значение П. т. За полный период оно равно нулю. Поэтому обычно вычисляют среднее значение положительной полуволны синусоидального П. т.

Т/2

г_ср.=ψ f I sin (cot, + φ) dt=J s 0,637/. о

Во многих задачах ищут среднее квадратичное значение тока. Так например, э ф-фективным, или действующим, значением силы П. т. называют силу постоянного тока, выделяющего за определенный промежуток времени в проводнике такое количество теплоты, как и данный П. т. Поэтому

1эфф. т

„ Р Sill² (ωί + φ) άφ =

V 2

Равпым образом эффективное значение напряжения и —U sin cof выражается через и^.=-₍7₂:=0,707П.

Измерительные приборы обычно показывают эффективные значения силы и напряжения П. т.

В электрич. цепях, содержащих последовательно включенные реостат с сопротивлением R, конденсатор с емкостью С и катушку самоиндукции с индуктивностью L (фигура 2), мгновенные значения силы тока г и напряжения и связаны ур-ием:

Фигура 2.

ИЛИ

между собою диференциальным

, т> л i т di, i* i dt

^u=^Rl + ^Ldt+J ~c’

r ^d2i. p di, 1 · ₌ du

τ ^л,цТ Λ* -if

dia

dt

Интеграл этого диференциального ур-ия состоит из двух частей: 1) установив

шегося тока, возникающего в цепи через достаточно долгий промежуток времени и не зависящего от начальных условий при включении цепи; установившийся ток определяется заданным напряжением и называется поэтому в ы-нужденным током; 2) переходного тока, определяемого как интеграл диференциального уравнения без правой части и зависящего от начальных условий включения. Переходный ток не зависит от заданного напряжения и называется поэтому свободным током. Энергия свободного тока с течением времени поглощается в цепи, так что через достаточно долгий промежуток времени свободные токи в цепи затухают. Действительный ток является в каждый данный момент времени суммой установившегося (вынужденного) тот и свободного тока.

Установившийся синусоидальный П. т. Если к=U sin со/, то диферен-циальное ур-ие принимает вид:

^L^+^Rm+iⁱ-^U(ocoscot·

Установившийся ток, удовлетворяющий этому ур-ию, определяется по ф-ле:

г=^Uz sin (ωί — φ), где _____

z-V ^R2+{L»-ch>Y

есть полное, или кажущееся, сопротивление данной цепи, а сдвиг фаз

Пси--¹-, С о)

φ=arc tg -д--

Т. о. в цепи П. т. сила тока отстает по фазе от напряжения на угол φ, называемый сдвигом фаз. Амплитуда силы тока получается путем деления амплитуды напряжения на кажущееся сопротивление г, называемое также импеданцем (смотрите). Частный случай: /i=0. Сила тока отстает от напряжения по фазе на угол ” или опережает напряжение на тот же угол, φ=— ”

в зависимости от знака разности La> - ₍¹^.

Отстающий ток называется индуктив-н ы м, а опережающий—е мкостаым. В обоих случаях ток, сдвинутый по фазе на

2 относительно напряжения, называется реактивным током (прежде говорили «безваттным»). Разность Leo— ~ называется реактивным сопротивлением, или реактанцем (прежде говорили «безваттное» сопротивление), и обозначается обычно буквой х:

х=Lay=хl Xq,

где x_L=Leo—и ндуктивное, х_с=—

емкостное сопротивление. Т. о. в цепи П. т. емкость компенсирует влияние индуктивности. В действительной цепи сопротивление всегда отлично от нуля, 11ф 0. Если R >0, то сдвиг фаз по абсолютной величине < При изменении частоты реактанц х меняет свое значение и обращается в нуль, когда т 1 1

Ζ-ίΟ=77- ИЛИ СО - ·

Сш J/L0

В этом случае в колебательных контурах получается совпадение частоты вынужденного и свободного колебания, или резонанс (смотрите)· Сила тока совпадает при х=0 по фазе с напряжением и получает наибольшую при данном сопротивлении амплитуду

Переходный ток. 1)Апериодич. случай: R²>~. Сила тока г определяется из формулы

-air 2Qo + IqCR, , _τ, Λ.

г=е 1“ ^silv< + Jochv/j;

здесь: 1₀—начальное значение силы тока, <?„—начальное значение заряда конденсатора С, v-V —Д- Д> α= -у —множитель г 4L·* L>L· 2L·

затухания.

2) Колебательный случай—R* < ⁴(^Л. Сила тока определяется по ф-ле:

г=^2Q ^- ^R sin γ t + Z₀ cosγ ή,

1 Ϊ Д2

где γ=у с£ — t_Li — круговая частота собственных колебаний иепи. Если можно пренебречь сопротивлением цепи, то у определяется по ф-ле

3) Критич. случай: Л²=_Q. В

т VQq + TqCFI ^J· 2CL

этом случае )·

Мощность П. т. Мгновенная мощность р, доставляемая цепи П. т., в которой действует напряжение и, определяется следующим выражением:

р=vi=U sin coil sin (cot — φ) =

= ~ [COS φ — COS (2ωί — φ)].

Мгновенная мощность пульсирует с частотой вдвое большей, чем частота тока. Среднее значение мощности: т

Р=} f иг dt=^ · J- · cos φ - г Ц_фф_.

Мощность П. т. равна произведению эффективных значений силы тока и напряжения на cos φ угла сдвига фаз между напряжением и силой тока. Множитель cos φ называется также коэфициентом мощности. Мощность П. т. можно тоже изображать при помощи вектора, имеющего длину, равную кажущейся мощности,!. е. произведению эффективных значений силы тока и напряжения и_эфф.-1_эфф. Проекция этого вектора на направление под углом ψ дает активнуюмощность U_Эфф. 1₃фф.· соя ψ. Проекция на перпендикулярное направление дает реактивную мощность и_эфф. 1„фф. - sin φ. Реактивная (прежде говорили «безваттная») мощность, как и активная, выражается в W.

Однако для различия принято кажущуюся и реактивную мощность измерять в VA. За последнее время распространяется также для единицы измерения реактивной мощности обозначение VAr, что означает — вольтамперы реактивные. Активную мощность молено также рассматривать как произведение вектора напряжения и“ФФ. ^на проекцию вектора тока на направление папряжения, 1_зфф, -cosy. Т. о. можно мысленно разложить силу тока на два составляющих тока: 1) активную составляющую с амплитудой 1 COS φ, совпадающую по фазе с напряжением, и

2) реактивную составляющую (прежде говорили «безваттную») с амплитудой 1 sin φ, опережающую напряжение или отстающую от него на “. В действительности по проводнику, понятно, проходит только один мгновенный ток, и разложение его на составляющие является удобным приемом для решения задач П. т. Подобно силе тока молено разложить на составляющие и напряжение: активная составляющая напряжения с амплитудой U cos φ совпадает по фазе с силой тока, реактивная составляющая с амплитудой U sin φ сдвинута относительно тока по фазе на ”.

Символический метод. Во многих случаях при решении задач П. т. приходится, не довольствуясь методом векторных диаграмм, прибегать к вычислению. В этих случаях удобным орудием вычисления является метод комплексных чисел (смотрите), позволяющий алгебраически учитывать фазу и амплитуду колебаний, подобно тому как это делается графически в векторных диаграммах. Векторы, изображающие периодические переменные величины, в спою очередь м. б. изображены при помощи комплексных чисел. Напр. комплексное число

У 21 cos (cot - φ) + j У 2 I sin (cot — <?>)=

= У 2 Ιβ^^ω1~^ψ^

(где j - y~ 1) изображает вектор, длина которого равна У Ш, а проекции на действительную и мнимую оси равны у 2 I COS (cot — φ) И У 21 sin (ωί — φ). Можно поэтому условиться, что это комплексное число будет символически изображать П. т., мгновенное значение к-рого г=У 21 sin (ωί - φ);

здесь У 2 I—амплитуда, а I—эффективное значение данного П. т. Можно еще больше упростить обозначения, если брать вектор, равный по длине не амплитуде, а эффективному значению I колебания, и в соответствующем комплексном числе

_1е1Ы-я>) „ _le-w. gjcol

отбросить множитель времени _ejoH, р_{огда комплексное} число

ϊ - ΐ6-’^φ

изображает символически силу тока i. Если этот ток проходит в цепи под влиянием напряжения и=У 2 U sin cot,

то это напряжение тоже м. б. изображено без множителя времени числом

ϋ-и.

Частное от деления напряжения U на силу тока i,

” J<P

= У COS φ + j у sin φ=Г + jx,

называется комплексным импедан-ц ем цепи. Его модуль г равен полному сопротивлению цепи. Действительная часть и у COS 95 ‘

г COS φ=г равна активному сопротивлению, а мнимая часть и.

У sin φ=Z sm φ=X

равна реактивному сопротивлению. Таким обр. комплексный импеданц является векторной суммой активной и реактивной составляющей сопротивления (фигура 3).

В комплексной же форме зависимость между напряжением и силой тока при П. т.

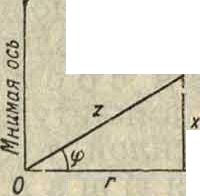
Дейстбит. ось

Характеристика цепи

Фигура 3.

сохраняет простую форму закона Ома: ΰ=I г.

Между символич. значением комплексных чисел ϋ и I, с одной стороны, и ζ—с другой стороны, существует различие. Векторы ϋ и I получены после условного сокращения множителя времени е^1Ы, тогда как вектор, изображаемый г. не зависит от времени.

В связи с этим различием^ часто считают выражения U, I не комплексными чи, а векторами, оставляя название комплексного числа за их отношением ζ, в котором множитель времени сокращается. Это различие несущественно, хотя многие видят в нем более «ясный» подход к символич. методу, чем при обычном пользовании комплексными чи.

Обратная величина комплексному сопротивлению, комплексная проводимость, или адмитанц (смотрите), определяется по следующей формуле:

ί-β-Λ.

X 7. *7.

При разветвлении тока общий ток равен векторной сумме токов в отдельных ветвях. Так например, если напряжение V приложено к 2 параллельным импеданцам (фигура 4), то

ίι=ύ(0ι-βι), ~ U(g₂-jb₂),

i=i,+и=tf[(_ffl + g₂) - j(b_t + b_a)], где

bi-

L o)

g 2 =

r 2

Z1^{7 x} Zi ⁷ z₂⁷ * Z₂

zl=rl + L]co², zl=r + L|co².

При диференцировании символич. выражений И. т. следует учитывать множитель вре-

/,.^L

гТЛЛР—АЯЯКЯЯГ

Фигура 4.

I,

мени е-

№

ком-

изображает то ~ изображает комплексное число ja>ld<-^ut~^v>=coIet(^cat4l‘*~i)’ откуда

Так, если 1 плексное число,

dl. _τ·

Τι ⁼ 1^ω1·

Производная по времени вектора П. т. опережает данный вектор на ” и имеет в ω раз

Способы вычисления комплексного сопротивления электрических цепей. таштажг-

L

ЛТДнАЛ-П-Л-,

Формулы для вычисления

2=г + jLco

• 1 I ¹

у “ Ί-⁺ jLH ‘

• jrLo) _ ^Z ~~ r + iLoi

• jLw

rjL(o

rL²a>² -f jr²Lro г^г + L²co“

, + jCoi =

1 + jrCco

2 =

r r - jr²C(o

l+jrC’io 1 + r²C²<u^z

• I

^y=r

Действительная часть этого выражения обозначается обычно буквой η и называется иногда копдуктанц (смотрите). Мнимая часть обозначается буквой b.

9 =_z^r, b=“, у=g — jb.

Применение комплексных чисел позволяет применять к установившимся П. т. не только закон Ома, но и правила Кирхгофа. Т. о. можно вычислить комплексное сопротивление ряда цепей (смотрите таблицу).

ббльшую амплитуду. Интегрирование как действие, обратное диференцированию, дает

fi dt=~ i=- j¹ i.

J Jio m

0

Интеграл по времени вектора П. т. отстает па ” от данного вектора и имеет в со раз меньшую амплитуду. Т. о. применение комплексных чисел превращает диференциаль-ные ур-ия И. т. в алгебраич. ур-ия, например ур-ие тока в электрич. цепи, содержащей сопротивление, индуктивность и емкость,

L ^dd + Ri + l f i dt=и превращается в алгебраич. ур-ие: j<oLi + Ri-jJ-i=ZJ,

ИЛИ

17-i[R + j(Lco-±)]-L·.

В более сложных случаях преимущества символич. метода проявляются еще ярче, например если параллельные цепи связаны между собой индуктивно с коэфициентом взаимной индукции М, то силы токов в этих цепях определяются следующими диферен-циальными уравнениями:

u-Rfr + L^+M^,

и=Т?₂г₂ + L_s +М ~·

При установившемся режиме получаются комплексные алгебраич. ур-ия:

u=(R₁ + jL,ω)ΐ₁ + j М coi г, и=(7f_a + jL₂cu)7₂ + jMwi_lt

откуда

j _ jj 1/л+нь2+п)++

¹ 3 ’

¹2~^U J >

где

s²=[RiRt - (T^L, - M)²co²]² + (BiLj +

+ RJ^o*.

Сдвиг фаз между Д и 7*_а зависит от ω и постоянных цепи. Можно определить М, при котором этот сдвиг фаз будет равен ”. Тогда Д=kj Д, а следовательно

kj (7?! + jLjo»)/, + jMcoit =

- (7?_а + ?Ь₂а))Д - kMcoi_%,

откуда

— kL/jj=Т?₂ — /сМси, /c/ϊ, + Мсо — L_aco

ИЛИ

м - 2 (1* + ь.) + - L₂)²-4·^.

Вычисление мощности. Если в электрич. цепи под влиянием напряжения fi - ГУе ~^)Vl проходит ток 7=7е^-т, то средняя (активная) мощность, потребляемая в этой цепи, равна

Р=U1 cos у, где φ=ц’_г — ψj.

Чтобы получить это выражение методом комплексных чисел, следует один из векторов, например ύ, помножить на сопряженное выражение другого, 7=7e^5V’². Тогда

ύ ί=υΡ^Κψ*~^Ψί)=UI cos φ + jUl sin «ρ. Действительная часть этого произведения дает активную мощность, а мнимая— реактивную.

ОбщаяцепьП. т. Целый ряд задач П. т. может быть сведен к простой эквивалентной схеме (фигура 5). К двум первичным зажимам А, В прилагается напряжение b. Тогда па вторичных зажимах С, D появляется напряжение Д₂, зависящее от Ь и от тока нагрузки 7"₂. Если известны и_г, Д, то этим определены Г7_1; Д. При холостом ходе (индекс 0) Д_>0=0,

Ul,0=$0^2,0} Д ,0=2/flH 2,0-

При коротком замыкании (индекс к) b’_2к=0,

^ ^_ 1к —%12ft, 1цс ⁼ ^к ·

где

«0=1+ 2/А, S*=1 + 2,

г ~Ζι + г₂ + Дг₂гД.

Между этими величинами существует следующая зависимость

s₀s_k-zy_a=1.

При любой нагрузке пользуются принципом наложения холостого хода и ко-

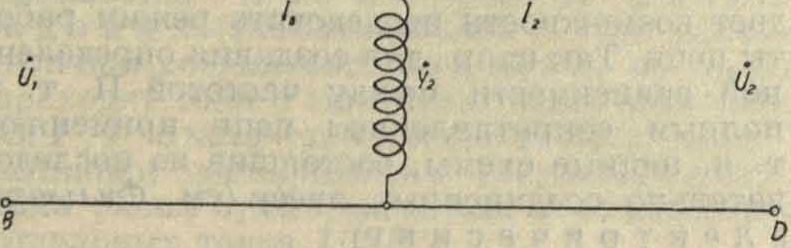
Фигура 5.

роткого замыкания: для любой нагрузки П_а, берут ύ_2>0=ϋ₂ и Ii_k=Ii, тогда получают первичные величины 1Д, 7, путем н а-л о ж е н и я обоих режимов:

= 77_1>0 -)- Ь _к — s₀ ΰ₂ + гД,

Д ” 7,.0 + Д*=УаР* + **Д ·

Эта общая цепь П. т. дает решение задач передачи энергии, преобразования энергии в трансформаторах и ряде электрич. машин.

При и_х=Const и при постоянном сдвиге фаз между Д и (Д конец вектора 1_Л описывает окружность (круг о-вую диаграмму), на которой можно определить графически значения 7*_а, П₂, вторичную мощность, потери и отдачу. Пусть г_п обозначает импе-данц нагрузки между С и D. При постоянном вторичном сдвиге фаз г_п сохраняет свое направление при из-Фпг. 6. менении нагрузки, и потому конец вектора г₂ + г„, изображающего общий импеданц, перемещается по прямой PQ (фигура 6). Конец обратного вектора. ¹ i- описывает следовательно окруж-

2i+Zn

ность, получаемую путем инверсии (смотрите) прямой PQ. Эту же окружность, но только смещенную на и„, описывает конец вектора у_а+. Инверсия этой окруяспости дает

+ 2 “Г Z_n

новую окружность, описываемую концом

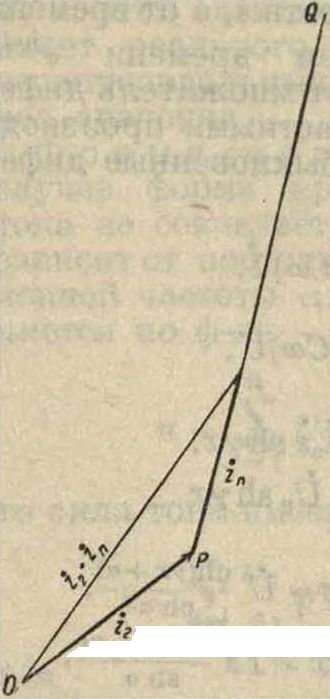
^z2 + Z_n

. Прибавляя

•обратного вектора

_β 1 "Ь У а + ^ζη·α

вектор %, мы смещаем всю окружность на г_х. Точки этой окружности соответствуют значениям полного импеданца цепи

«I ^гb + ^ХП

Ί----· · ·

1 + ²2’1а + ²пУа

Третья инверсия превращает этот импеданц в вектор полной проводимости всей цепи, изображающий в соответствующем масштабе силу тока Д. Окружность, описываемая концом вектора 1_и со всеми вспомогательными линиями, позволяющими графически определять ряд элементов работы цепи, называется круговой диаграммой цепи. Существуют способы для весьма простого построения круговых диаграмм, излагаемые в учебниках. В более сложных случаях применение обшей цепи П. т. не дает возможности исследовать режим работы цепи. Так например,для создания определенной зависимости между частотой П. т. и полным сопротивлением цепи применяют т. н. цепные схемы, состоящие из последовательно соединенных ячеек (смотрите Фильтры, электрические).

Линии с распределенными постоянными. В длинных линиях или при большой частоте П. т. постоянные линии нельзя считать сосредоточенными. Пусть г, д, L, С обозначают соответственно сопротивление, утечку, индуктивность и емкость, приходящиеся на единицу длины линии. Сила тока г и напряжение и удовлетворяют тогда диференциальным ур-иям:

0и. _Т di di i _п ди

~M=ⁿ + ^LTi’ ~bх ⁼ 9“+^СЛ’ где ж—расстояние точки наблюдения от начала линии. При установившемся синусоидальном режиме зависимость г, и от времени определяется множителем времени e^lmt. После сокращения на этот множитель дифе-ренциальные ур-ия с частными производными превращаются в обыкновенные дифе-рснциальные ур-ия

-f_x=(r+jLc»)i,

di

dx

^; (g + jC(o)U,

откуда или

U=Г/₀ ch γχ - I₀z sh уж, ΐζ=ΐ₀ζ ch γχ — ϋ„ sh γχ

сШуж + al

U₀=V ch γχ -)- lz shycc=V

ch a

sh(yX + O

I₀z=lz chyx -И/oShya;=1ζ· _gllaгде ύ₀,ΐ₀ — значения ϋ,ί в точке ж=0; ζ=· г +зХш__хар_актер_ИСТИКа линии, или волновое сопротивление; γ=V (г + jLa>) (д + jCaj); th a=-4-.

Существуют номограммы, позволяющие определять графически а, а затем распределение U, 1 в ф-ии от расстояния х. Эти номо граммы основаны на свойствах гиперболических ф-ий комплексного аргумента. Подробнее см. Линии передачи, Линии связи. Сети электрические.

Символический метод при затухающих колебаниях. Колебательный затухающий ток г=le~^al sin (ωΐ— φ)

можно тоже изобразить при помощи комплексного числа:

[J]=Ιβ~^α1β^ί(·^ω1~^ψΚ

Тогда

.-(-«+ #ю) Ιβ-βΚ"*-’)=(- a + }b)[Л. Поэтому диференциальное ур-ие цепи и=М + L ^dJ_t

преобразуется в алгебраическое [U]=(R-La + jLa>)[I], так что комплексный импеданц для затухающих колебаний в цепи, содержащий R L, м. б. изображен при помощи комплексного числа

R— La -f- jLcо.

Этот метод можно применять и при более сложных задачах.

Многофазные токи. Если на роторе двухполюсной электрич. машины вращающемся в равномерном магнитном поле, расположено п симметричных обмоток, то в этих обмотках наводятся напряжения, изображаемые комплексными чи

ύ_λ=Ι/β^{3(ωί + λψ)} (λ=1, 2, .,η),

где Я—порядковый номер обмотки, у> « ²^ —

сдвиг фаз между напряжениями двух соседних обмоток. Сумма этих п напряжений равна 0:

ύ₁ + ν₂ +. + ν„=0,

так что из этих обмоток можно образовать замкнутое кольцо, соединяя их последовательно. Результирующее напряж ение, равное векторной сумме сторон правильного η-угольника равно нулю, так что в такой замкнутой обмотке не будет проходить ток (соединение мн-ком). Можно однако соединить вместе начальные точки всех обмоток, так что их напряжения будут изображаться симметрично расположенными радиусами-векторами (соединение звез-д о й). Совокупность этих обмоток образует я-фазну ю систему П. т., а отдельные обмотки системы образуют фазы этой системы. Если нагрузить одинаково все фазы симметричной системы, то в каждой фазе возникает ток, изображаемый вектором

j _ Ч*=1_е + *v-<p).

^λ ζ

Мгновенная мощность каждой фазы равна ρ_λ=ϋ ] 21} 2 sin (cot + λψ) sin (coi + λψ— φ)== UI[COS φ — COS (2coi + 2λψ — φ)], а мгновенная мошность всех п фаз равна сумме Р=2рд=nUI cos φ. Т. о. мгновенная мощность системы равна сумме средних мощностей отдельных фаз и сохраняет постоянное значение независимо от времени

(уравновешенная система). Уравновешенной м. б. при известных условиях и несимметричная система. Осо :енное значение имеет в технике трехфазная система (смотрите Системы переменного тока).

Несинусоидальные П. т. Применяемые в технике П. т. в действительноеги всегда б. или м. отклоняются от синусоидально! формы. Если отклонения принимают значительные размеры, то кривая П. т., как всякая периодич. кривая, м. б. разложена на основную синусоидальную волну и на ряд синусоидальных высших гармоник (смотрите Тригономенгрические ряды):

СО

г=2 ^:i> V- ^si[1 (Ρ^ωί + <Рр) =

Р — 1

со

= 2 (a_r sin ρωΙ + b_p cos ρω/),

P=1

где

Л η

πα_ρ=J ΐ sin ρχ dx, лЬ_р - |* i cos ρχ dx. о 0

На основании общих свойств тригонометрических рядов эффективное, то есть среднее квадратичное, значение несинусоидального тока, равно корню квадратному из суммы квадратов отдельных гармоник:

I=П + Ц+.

Средняя мощность несинусоидального П. т. равна сумме средних мощностей отдельных гармоник:

Р=IiUj cos ψ_λ + I₂U₂ cos <р₂ + ., где эффективное значение кривой напряжения определяется также по ф-ле:

U^e= U?+ Ui +.

По аналогии с простыми П. т. средняя мощность несинусоидального П. т. выражается в виде

Р=kUI,

где fc=cos ψ является коэфициентом мощности, то есть множителем, на который надо помноясить UI, чтобы получить Р. Здесь φ не является углом между действительными векторами П. т. Большинство практич. построений и расчетов с несинусоидальными П. т. производится однако с эквивалентными синусоидальными векторами, имеющими эффективные значения U, 1 и составляющими между собою угол φ, определяемый из равенства

k=COS Φ=^¹^¹°^08φι + Рг^2С08Уг+··· _<

⁹ у 0 +щ+~.у~ц + /?+.:

По этим данным определяют: результируίου

щее полное сопротивление г=_t, резуль-

р тирующее активное сопротивление г=,-_а =

= Y cos ψ, результирующее реактивное coin

противление х=_l sin φ.

Активн. сопротивление несинусоидально-го П. т. отличается от сопротивления синусоидального П. т. тем, что вытеснение тока (смотрите Скин-эффект) различны образом сказывается на различных гармониках. Только в том случае, если пренебречь этим различием и считать г постоянным, можно написать

U COS φ=Ш=ущ COS² Ψ₁ + Z7§COS² ф_г +. ; аналогично

U sin φ=yu² sin² <py + ?7|sin² φ₂+. Отсюда эквивалентное реактивное сопротивление

U sin φ

X - —

По реактивная мощность эквивалентного тока не равна сумме реактивных мощностей отдельных гармоник:

TJ1 sin ψ=F 2 U_; Ι_λ sin φ_λ. Множитель

F =

ущуущ где хя - λ [.со -

>.Сш ’

называется множителем расхождения (Induktionsfaktor). При параллельном соединении двух цепей, по которым проходят токи с эквивалентными значениями Г, I" с коэф-тами мощности cosy/, cosy/, активная составляющая результирующего тока равна сумме активных составляющих отдельных токов Г, I":

1 COS φ=Г COS φ + I" COS φ".

При сложении реактивных составляющих следует принимать во внимание различные множители расхождения F, зависящие от постоянных цепи, так что

FI sin ψ=FT sin φ + F"I" sin ψ". Обычно принимают для упрощения F=F=F".

Только в этом случае молено написать 1 sin Ψ=Г sin φ’ + J" Sill φ".

T. о. угол сдвига ψ эквивалентных П. т. не имеет реального значения, и диаграммы несинусоидальных П. т. имеют приблинсен-ное значение.

Форма кривой тока. В общем случае форма кривой несинусоидального тока не совпадает с кривой напряжения и зависит от постоянных цепи г, L,C и от основной частоты ω. Если напряжение изменяется по ф-ле и -

η

2 i/_A^2sin {λωΐ + ψ,),

Я=1

то сила тока имеет вид

ΎΙ гг

¹=Σ г, i^{72 sin} (^ш+ч>>. - νλ)-

Я=1

где

ζ=г² + (λΐω -, tg _{Ψλ τ}^λ·- ·

При индуктивной нагрузке последовательные амплитуды силы тока равны

ViUi VeUz У Ua

У Г* + ’ J Г> + iL*(0* У г2 +

При индуктивной нагрузке амплитуды высших гармонических кривой тока сглаживаются по сравнению с кривой напряжения. б т. Э. m. XVI.

При емкостной нагрузке амплитуды последовательных гармоник силы тока равны:

γΐϋι |/~2 U_s _ Ϋ2Е7₃

^Г2 + С2ш2 ^Г2 + 4С2щ2 |/~^г2 + ₉С2_Ш2

При емкостной нагрузке амплитуды гармоник тока имеют большее значение у кривой тока, чем у кривой напряжения; происходит искажение кривой, особенно заметное при малом сопротивлении. В большинстве технических П. т. вторая полуволна тока повторяет первую, но с обратным _ знаком, так что

Фигура 7.

В этом случае в разложении /(/) имеются только нечетные гармоники. Если в начальный момент отсчета времени /(0) равно 0 и если кроме того кривая симметрична относительно начальной точки,

/(-«)=-/(*),

то разложение кривой будет состоять исключительно из синусоид нечетного порядка:

г=Ij^sincot + I₃ sin 3ωί + 7₅sin5cui +.

Кривая считается практически синусоидальной, если ни одна из ее ординат г не отличается от соответствующей ординаты основной волны г_х больше чем на 5 % от амплитуды j/2X, этой основной волны. Для характеристики несинусоидальных кривых П.т. пользуются следующими коэфициента-ми. а) Коэфициент искажения: отношение эффективного значения основной волны к эффективн. значению эквивалентного вектора:

Фигура 8.

/й-ϊ¹·

б) Коэфициент амплитуды: отношение максимального значения к эффективному

i hna.

/a i

в) Коэфициент формы: отношение эффективного значения к среднему за положительную полуволну

h=γ—·

^lcp·

Для синусоиды

/, —1,11, /„=1,41, ft- 1. Некоторые разложения. 1) Прямоугольники (фигура 7):

У - * Y_m(sincot + *sin3cot + .),

/*-1. /«-1-

2) Равнобедренные тр-ки (фигура 8): у - (sin cot, -·sin 3cot + ~ sin 5coi — .).

3) Трапеции (фигура 9):

У ⁼ _ла ~j!~ C^-i ^siⁿ + -4₃ sin 3ωί + .), где

^4-2/i + i=(2fe jl 1)2 ^siⁿ + 1)2яД, β_Ι=“.

На практике часто встречается трапеция, у которой β=^ Τ’; тогда

i=1.053Г», (sin cui — sin 5ωί + i sin 7ωί — -^7Sin llcuf + .), /j=1,06, f_a=1,59.

4) Параболы (фигура 10):

У=^ (sin cot + — sin 3ωί + ^ sin 5ω< +. V

Дальнейшие примеры—см. Тригонометрические ряды.

Кроме П. т., среднее значение которых за полный период равно нулю, в технике встречаются волновые токи, когда на

ток, имеющий постоянное направление, накладывается синусоидальный или несинусоидальный П. т., например и=U₀ + Uj j/2 sin cot + U₂l 2 sin (2 ωΐ + ψ).

Измерительный прибор постоянного тока, покажет для такого колебания значение U₀, тогда как прибор П. т. покажет эквивалентное эффективное значение:

ϋ-γΰΐ + ΌΙ + Щ.

Такие волновые токи встречаются при выпрямлении П. т. Обычной причиной искажений П. т. является несинусоидальность. наведенного в генераторах П.т. напряжения и кроме того непостоянство характеристик г, С, L рассматриваемой цепи, например зависимость L, при наличии железа, от силы тока. Изучение П. т. с нелинейными характеристиками требует специальных исследований. На практике оно большей частью· проводится графически. Анализ кривых, получаемых при помощи измерительных приборов, —см. Гармонический анализ и, Тригонометрические ряды.

Лит.: Круг К. А., Основы электротехники,

2 изд., М., 1926; Френкель А., Теория пере-· менных токов, пер. с нем., М.—Л., 1928; Жане П., Общий курс электротехники, т. 2, пер. с франц., М.,. 1929; Черданцев И. А., Теория переменных токов, 2 издание, М.—Л., 1927; Рюденберг Р., Явления неу становившегося режима в электрических, установках, М,—Л., 1930; Widmar М., Vorle-sungen (iber die wissenschaftlichen Grundlagen d. Elektrotecbnjk, Berlin, 1928; Kennelly A. K. The Application ol Hyperbolic Functions to Electrical Engineering Problems, New York, 1925; S t e i n-m e t z С. P., Theory a. Calculation ol Alternating Current Phenomen, 5 ed., N. Y., 1917; Cohen L., Formulae a. Tables for the Calculation of Alternating Current Problems, N. A⁷., 1913; Emde F., Sinus-relief und Tangensrelief in d. Elektrot.echnik, Braunschweig, 1924. Я. Ш пильрейн.