 > Техника, страница 70 > Периодические функции
> Техника, страница 70 > Периодические функции
Периодические функции
Периодические функции, ф-ии, не меняющие своего значения при увеличении аргумента на постоянное число т, то есть удовлетворяющие условию: /(ж + тонн)=/(ж) для всякого х; τ называется периодом. График П. ф. представляет неограниченное повторение одного куска кривой, перенесенного вдоль оси ж-ов на длину τ,2τ,.,—τ,. (смотрите фигура). Если П. ф. имеет период т, то
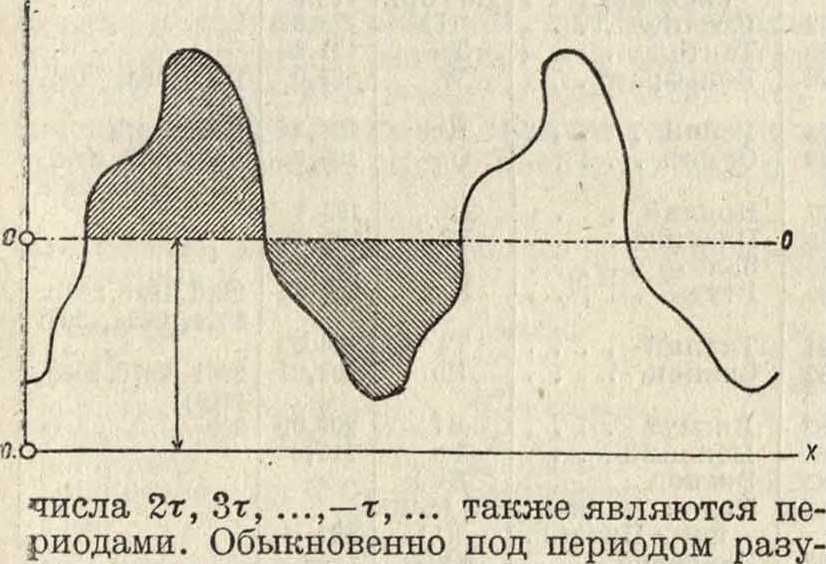
меют наименьший положительный период. Простейшие П. ф.—тригонометрические ф-ии <см. Тригонометрические функций)·, sin ж и cos ж имеют период 2л sin (ж+2я)=з1п ж, cos (ж+2я)=со.ч ж. Ф-ии sin пх и cos пх имеют период (наименьший); при η целом они допускают также период 2л. Это обстоятельство имеет большое значение для выражения произвольной П. ф.: произвольная П. ф. с периодом 2л, при нек-рых дополнительных условиях, м. б. представлена в виде ряда, содержащего постоянный член и члены с sin пх, cos пх (п=1, 2,3, .) с постоянными коэф-тами (смотрите Гармонический анализ, Ряды Ф у р ь е). П. ф. имеют большое применение в физике и механике для описания периодич. процессов (колебаний); если явление имеет период Т, то основными П. ф. яв-ляются sin γ, cos-y-(£—независимое пере-
менное, время; см. Маятник). После тригонометрия. ф-ий важным классом П. ф. являются эллиптические, или двоякопериодические, функции (смотрите Эллиптических функции). Здесь рассматриваются также комплексные значения аргумента г; два периода 2ω, 2готоже, вообще гово ря, комплексные; двоякопериодич. функции /(г) определяются условиями: /(г + 2си)—/(г), /(г + 2со)=/(г). В последние годы датский математик Гаральд Бор изучил новый класс ф-ии—п о чти-п ериодические ф-ии. Их определение такого: /(ж) является почти периодической ф-ией, если для всякого малого положительного числа е можно найти такие числа τ («почти-периоды»), что для всех ж имеет место неравенство: |/(ж + тонн)-/(ж)| < е; при этом разные почти-периоды, соответствующие данному е, должен быть расположены не реже некоторой арифметич. прогрессии. Простейшими почти-периодич. ф-иями являются суммы II. ф. с несоизмеримым отношением периодов, например A sin ах+В sin βχ, если "
иррациональное число. Доказывается, что любая почти-периодическая ф-ия м. б. представлена бесконечным рядам Фурье вида
СО
2 («„cos ληχ+ b„sin ληχ), где Α„—любые дей-
η=1
ствительные числа (если Яп целые, то получим П. ф.). Почти-периодич. ф-ии встречаются в ряде проблем динамики.
Лит.: Привалов И. И., Ряды Фурье, Москва— Ленинград, 1930. В. Степанов.