 > Техника, страница 71 > Планиметр
> Техника, страница 71 > Планиметр
Планиметр
Планиметр, инструмент для механич. определения площадей фигур на бумаге в мелких квадратных единицах (см, миллиметров) или в земельных мерах (га, м2). П. подразделяются на две группы: полярныеП., которые при употреблении вращаются около одной неподвижной точки (полюс), и линейные, перемещаемые по плану параллельно своему первоначальному положению.
А. Наиболее распространены в геодезич. практике полярныеП.; лучший из них компенсационный!!, механика Коради: он является усовершенствованным видоизменением П. Амслера. П. Коради существуют двух видов: 1) с постоянным рычагом и 2) с переменным; они различаются между собой устройством свободного рычага и расположением счетного механизма относительно точки пересечения рычагов.
П.с постоя ни ым рычагом (фигура 1) состоит из двух отдельных рычагов, к-рые
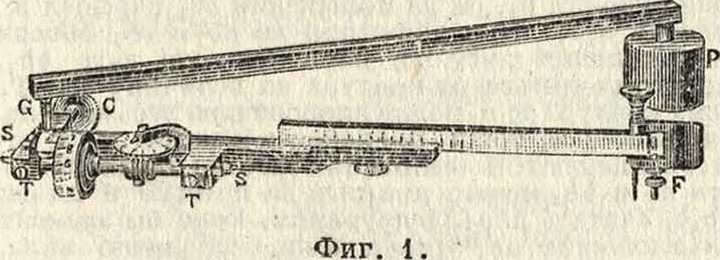
для работы составляются вместе. Один из них называется полюсным, другой— обводным. Полюсный рычаг—металич. брусок, к одному концу которого приделан медный цилиндр Р. Снизу цилиндра, в его центре, вделана тонкая игла (полюсП.), которая во время работы вдаливается в бумагу и остается неподвижной. Для уменьшения трения низ цилиндра Р сточен т. о., что в средине получается небольшой выступ, перпендикулярный к направлению рычага. На другом конце бруска прикреплен конич. формы стальной отросток G, оканчивающийся шариком. При соединении рычагов этот отросток вкладывается в гнездо обводного рычага полушарообразной формы. Обводный рычаг состоит из двух частей. Одна часть—небольшой брусок такого же вида, как и у полюсного рычага. В свободном конце его вставлен обводный шпиль (игла) с небольшой пружиной и грифом F. Этот гриф держат пальцами при обведении фигуры. Снизу грифа ввинчивается подставка, устанавливаемая так, что обводный шпиль только слегка касается бумаги и не царапает ее. Сбоку этого бруска нарезана полумиллиметровая шкала для установления обводного рычага на определенную длину. Другая часть обводного рычага представляет собой металлич. отлив с тремя выступами. В удлиненном его конце сделан желобок, в к-рый· вставляется брусок, с обводным шпилем и закрепляется винтом, проходящим снизу. Между выступами Т, Т помещается счетный механизм, состоящий из циферблата, счетного колеса и верньера (смотрите). Счетное колесо (валик) наглухо скреплено с осью, в средине которой сделан бесконечный винт. Концы оси конич. формы входят в углубления небольших подшипников. С помощью винтов S, S можно изменять положение этих подшипников и сообщать оси продольное перемещение. Счетное колесо цилиндрич. формы, с металлич. ободком, сделано из белого цел-люлоида. Поверхность колеса разделена на 100 равных частей и занумерована через каждый десяток деления цифрами 0—9. Для-, оценки десятых долей деления колеса рядом с ним установлен верньер. У первого штриха верньера подписана цифра 0 и у последнего 10. К бесконечному винту оси счетного колеса прилегает шестерня, скрепленная с осью вращения кружка (циферблата). Поверхность кружка разделена на 10 равных частей, отмеченных цифрами 0—9. Сверху кружка через его центр проходит отросток, оканчивающийся острием, которое служит указателем (индексом). Бесконечный винт и шестерня сделаны с таким расчетом, что одному полному обороту счетного колеса соответствует 0,1 полного оборота циферблата. Счетный механизм дает возможность считать полные обороты счетного колеса (по циферблату), десятые и сотые доли его оборота (на самом валике) и тысячные доли его оборота (по верньеру). На свободном выступе свободного рычага помещается опорное колесо С, вследствие чего вся тяжесть П. распределяется на 4 точки опоры: полюс, свободный шпиль, ободок счетного колеса и опорное колесо.
П.с перемени ым ры ч а гом (фигура 2) отличается от описанного устройством обводного рычага. Этот последний состоит из длинного бруска FL (—23 см) с изогнутым
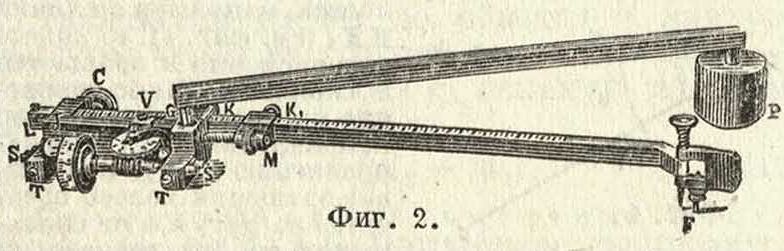
концом, в к-рый вставлен обводный шпиль F. Для соединения со счетным механизмом рычаг вставляется в 2 муфты, находящиеся на противоположной стороне выступов Т, Т,
и закрепляется двумя нажимными винтами К (второй винт находится на выступе с опорным колесом С и на фигуре не виден). Для сообщения рычагу медленного движения, он вкладывается в третью муфту М с нажимным кинтом Κχ. При помощи микрометрического винта, обвитого пружинкой, муфта М соединяется с выступом Т. Чтобы устанавливать рычаг на определенную длину, на верхней его грани нарезана полумиллиметровая шкала, а сверху рамы счетного механизма прикреплен верньер V. Для такой установки ослабляют нажимные винты К, КJ и движением руки устанавливают рычаг сначала грубо на требуемую длину; затем, закрепив винт К1, действуют гайкой при муфте М, устанавливают рычаг точно по верньеру и закрепляют нажимные винты К. В других деталях П. с переменным рычагом подобен вышеописанному П. с постоянным рычагом.
При соединении рычагов свободный рычаг будет вращаться около воображаемой оси, проходящей через центр шарика, к-рый находится на конце отростка О, и перпендикулярной к плоскости чертежа. Эту линию называют осью вращения П. Расстояние от оси до полюса примем за длину полюсного рычага, а расстояние от оси до обводного шпиля—за длину обводного рычага. Чтобы практически получить длину обводного рычага, устанавливают на бумаге этот рычаг и делают 2 накола—обводным шпилем и иглой—через отверстие, просверленное в шарообразном гнезде рычага. Последний накол будет проекцией оси вращения. Расстояние между наколами принимают за длину обводного рычага. Для получения длины полюсного рычага удерживают в том же неподвижном положении обводный рычаг, осторожно вкладывают в гнездо отросток О, нажимают цилиндр Р и получают полюс П. Расстояние между полюсом и проекцией оси вращения есть длина полюсного рычага.
Т е о р и я П. разрабатывается при условии, что плоскость ободка счетного колеса перпендикулярна к направлению обводного рычага. 1) Положим, обводный рычаг перемещается параллельно самому себе
Т
К
~г
%
~Л~
-ь
% Фигура 4.
Фигура 3.
ш из положения 1 перейдет в положение II (фигура 3). При этом ободок счетного колеса К обернется на такую дугу и своей окружности, которая равна перпендикулярному расстоянию h между 1и II положениями:
u=h. (1)
2) Если обводный рычаг перемещается параллельно ^самому себе, но под углом к направлению счетного колеса, например по линии К К 2 (смотрите фигура 4), т > колесо одновременно и вращается и скользит. Такое движение разлагается на два: по направлению КК^ и по направлению К К %. Вследст-- вие вращения колесо обернется на дугу/г, а от скольжения оно не сделает ни •сдного оборота. Следовательно и в этом случае
u=h. (2)
.3) Если обводный рычаг вращается около некоторой точки а и из положения аЬ перейдет в положение ас
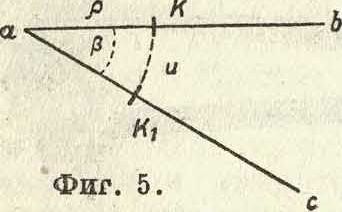
(фигура 5), то счетное колесо К переместится в К±, обернувшись нд дугу и. Длина дуги и будет зависеть от расстояния колеса К до точки а. Обозначив это расстояние через ρ, дугу при радиусе, равном единице, соответствующую углу Ьас, через β, имеем:
Κ=βρ. (3)
4) В общем случае, когда обводный рычаг из какого-либо положения перемещается в другое произвольное,
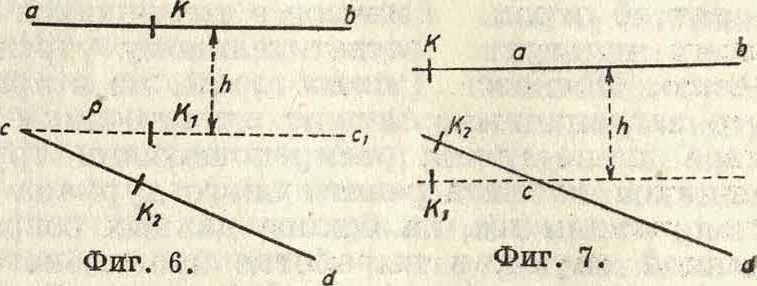
например из положения аb в положение cd (фигура 6), такое движение можно разложить на два: сначала считать, что рычаг из положения ab передвинулся параллельно самому себе и занял положение cclt а затем, повернувшись около точки с перешел в положение cd. На основании предыдущего дуга, на которую обернулось колесо К при переходе из Е в К2, выразится:
U^h+βρ. (4)
Для П. с переменным рычагом формула (4) обратится в U=h — βρ (5)
вследствие того, что счетный механизм в таком П. находится за точкой пересечения рычагов, и при вращении обводного рычага около точки с на дугу β (для перехода из ссх в cd) счетное колесо будет вращаться в об-. ратную сторону против вращения, когда оно переходило из ab в ccj (фигура 7). При движении обводного шпиля по контуру фигуры счетное колесо будет и вращаться и скользить. Т. о. путь, пройденный колесом на бумаге, вообще будет более (иногда равен) дуги, на к-рую счет-пое колесо обернется при своем перемещении.
Положим, требуется вычислить площадь фигура 8. Установим П. так, чтобы его полюс Р находился внутри фи-гуры. Обводный шпиль по- Фигура 8.
ставим в точку а контура фигуры. П. займет положение аЬР, причем ab =Д есть свободный рычаг и ЬР=—полюсный. Пере двинем обводный шпиль на очень малую часть контура acidi и поставим его в точку аг. П. займет положение а1Ь1Р и про идет элемент площади abPbi^c^a. При этом точка b пересечения рычагов переместится в Ьь и полюсный рычаг Rx пройдет площадь сектора Движение обводного рычага k из ab
в axbi разложится на два: 1) обводный рычаг R из положения ab передвинулся в положение сЬг параллельно самому себе и 2) повернувшись около неподвижной точки blt он из положения cb1 перешел в положение atb1. При движении из ab в cbx обводный шпиль опишет дугу ас, параллельную дуге bb1} и будет отклоняться от контура на величину ccj. Т. к. длина контураacjai по предположению весьма мала, то уклонением cci можно пренебречь и считать, что точки с и ci совпадают. На основании того же предположения дуги ас и bbi можно принять за прямые и площадь abblc1 считать параллелограмом. Если бы элементарная площадка аЬРЬια^α была бесконечно мала, то такие допущения были бы совершенно точны. Т. обр. элементарная площадь разделилась на три площади: параллелограм аЬЬгс и два сектора bРbг и cbjaj. Обозначим элементарную площадь abPbia1c1a через Р, дугу при радиусе, равном единице, соответствующую углу cbiai, через β· дугу при таком же радиусе, соответствующую углу b Pbit через φ. Удерживая прежние обозначения, будем иметь:
р=ДЬ+| cai-R+- bbi-Ri. (6)
В этом выражении, на основании (4) Η=ιι+βρ. На основании пропорциональности дуг своим радиусам сах=βϋ и bbl=<pRx Подставив эти выражения вместо равных им в ур-ие (6), будем иметь:
p^Ru-RPe + ^W + ^fR^ (7)
Передвинем обводный шпиль также на1 весьма малую часть контура α^. П. займет положение а2Ь2Р, прой-
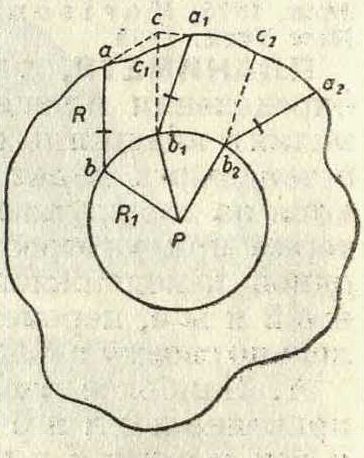
дя новый элемент площади aic^baPbiGi· Этот элемент подобно предыдущему можно разложить на 3 площади и выразить ф-лой, подобной формуле (7). Т. к. часть контура αια2 вообще не равна части aalf то новый элемент площади не равен предыдущему, и в выражении этой площади величины и, β и <р будут иные. Обозначив через Ρι элементарную площадь a^b^Pbiа1: будем иметь:
p1=Rui - Rβle +2^iR2+2,’iri
Для следующего элемента площади получим
Р2=Ru% — Rβ2Q + 2 02jH2 + VzRl
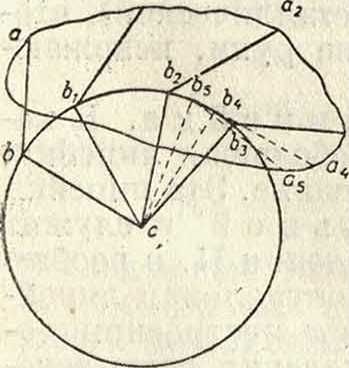
ит. д. По обведении обводным шпилем всего контура П. пройдет ряд элементарных площадок и займет первоначальное положение abP.Чтобы получить выражение всей площади фигуры, надо взять сумму выражений всех элементарных площадей. Складывая почленно предыдущие выражепия, будем иметь:
Р+РХ + Р2 + -·.=й(и+«!+ «2 + .) —
“ Дв(0 + 01+02 + ···) + 2 ^2(0 + 0 1 + 02 + ···) +
+ 2^ΐ(Τ,+ ¥ι1+4!2 + .). (8)
В этом выражении Р+Р1+Р2 +. дает общую площадь Р фигуры. Сумма u+Ui +. представляет сумму дуг, на к-рую обернулось счетное колесо при обведении всего контура и к-рую обозначим через U. Суммы 0 + 01 + 02 +. и 9>+?ч+ 9>2 +··· выражают суммы дуг при радиусе, равном единице, и каждая в отдельности равна 2π. Что сумма φ+^ι-Κ. равна 2л, видно из чертежа, т. к. точка пересечения рычагов Ь при полном обведении контура опишет полную окружность. Для доказательства того, что сумма 0 + 0,+. равна 2л, возьмем произвольную точку и из нее проведем линии, параллельные всевозможным положениям обводного рычага. При точке построятся углы, соответствующие величинам β, 0, 02.При полном обве дении контура сумма построенных углов будет равна 360°, и сумма дуг, им соответствующих, при радиусе, равном единице, будет равна 2л. На этом основании формула (8) представится так:
Р=ЙС7-2л-й® + лН2 + яйх,
или
Я=йи + я(К2 + й!- 2Й®). (9)
Для П. с переменным рычагом последний член в скобках на основании ф-лы (5) будет иметь положительный знак, и формула (9) представится в таком виде:
Р= ЯЕ7 + л(К2"+й? ±2Ηρ): (10)
Формула (10)является общей для обоих видов П. Второй член формулы (10), зависящий от размеров П., есть величина постоянная. Обозначив его через Q, будем иметь:
P=RU+Q. (И)
Для исключения постоянного Q из формулы (И) поставим полюс П. вне контура фигуры в точку с (фигура 9) и обводный шпиль в точку а контура. При обведении контура по ходу часовой стрелки обводный шпиль будет проходить через точки a, alt «2, лежащие на верхней части контура. П.будет занимать при этом положения аbо, и т. д. Об водный шпиль, дойдя до некоторой предельной точки, например а3, будет двигаться по нижней части контура, и П. будет перемещаться в обратном направлении. При движении обводного шпиля по верхней части контура пространство между начальным и последующими положениями рычагов будет увеличиваться, то есть бу дут увеличиваться до некоторого предела суммы: β + βι + β% +. φ + ψι + ч>2 +. При движении шпиля по нижней части контура это пространство будет уменьшаться, и когда П. займет первоначальное положение abc, суммы β + βί+ ·, ψ + Ψι+··· обратятся в нуль. Вследствие этого в формуле (8) три последних члена, содержащие β и φ, обратятся в нуль, следовательно обратится в нуль постоянное число Q=n(R2 + + Rj±2Rs); формула (11) примет вид
P=RU. (12)
Итак, для вычисления площади фигуры имеем две формулы: при установке полюса внутри фигуры—ф-лу (11) и при установке полюса вне ее контура—ф-лу (12). При измерении площадей выгоднее полюс П. ставить вне контура фигуры. Кроме того при вычислении площадей старыми П., у которых концы оси счетного колеса достаточно износились, замечается продольное шатание оси. В таком случае расстояние между точкой пересечения рычагов и счетным колесом постоянно изменяется, то есть ρ является величиной переменной и само постоянное число Q—ненадежным.
Практическое пользованиеП. Соединив рычаги, выбирают место для постановки полюса по возможности вне контура фигуры. После установки полюса делают пробное обведение фигуры по ходу часовой стрелки. Если окажется, что при обведении рычаги составляют между собой слишком острые или тупые углы, то положение полюса меняют. Выбрав окончательно место для полюса, устанавливают обводный шпиль в одну из точек контура, к-рую считают начальной, и делают отсчет.
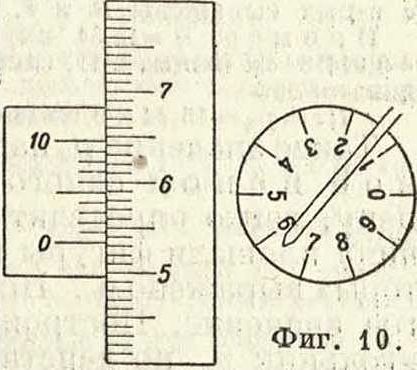
Допустим, что циферблат и счетное колесо расположились так, как показано нафигура 10. Отсчет делают так:сначала смотрят на циферблат и с него берут цифру, меньшую из тех, между к-рыми находится индекс (в данном случае 6). Затем смотрят на счетное колесо и записывают меньшую цифру из тех, между которыми находится нулевой штрих верньера. На фигуре 10 это цифра 5 (десятые доли оборота колеса). Отэтой цифры считают по черточкам сотые доли—их будет 4. После того по верньеру оценивают тысячные доли оборота,к-рых будет 6 (т. к. совпадает 6-я черта). Полный отсчет будет: 6 546 (тысячных). Сделав отсчет, осторожно обводят шпиль по контуру фигуры, двигая его по ходу часовой стрелки. Доведя обводный шпиль до начальной точки, снова делают отсчет указанным способом. Пусть этот отсчет будет 7 907. Разность отсчетов, равная 1 361, укажет, что ободок счетного колеса при обведении контура обернулся на 1з?1 тысячную своей окружности. Для получения плошади в натуральных (мелких) или земельных мерах эту разность надо умножить на некоторый коэфмциент.
Обозначив отсчет до обведения контура фигуры через mlt отсчет после обведения— через т2 и коэф. через к, искомую площадь Р выразим след, обр.:
Р=к (m2 - m-j). (13)
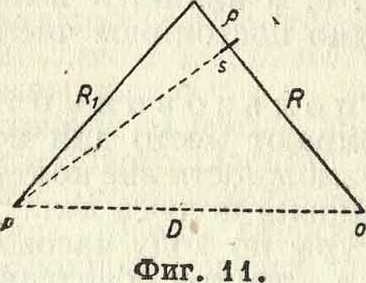
Геометрическое значение постоянного числа Q. Поставим рычаги планиметра Под таким углом, чтобы воображаемая плоскость ps (фигура 11), проходящая через ободок счетного колеса, прошла через полюс. Составится остроугольный тр-к, в котором обводный рычаг R может служить основанием и ρε—его высотой. При таком положении ры-
Фигура 9.
чагов расстояние между полюсом р и обводпым шпилем о, равное D, будет величиной постоянной. Применяя теорему геометрии о квадрате стороны, лежащей против острого угла, будем иметь:
Вг=Е2 + д2_2йг.
Для П. с переменным рычагом, у которого счетный механизм расположен за точкой пересечения рычагов и угол Ь тупой, последний член 2Rе будет иметь положительный знак. Предыдущая формула будет общая для обоих видов П. и представится так:
D2=Ra+Ri±2Rg.
Это есть тот трехчлен, к-рыЯ в выражении постоянного числа Q заключается в скобках (формула 1U). Заменяя его через, 232 будем иметь:
Q=.4(R2-f 2?2±2Ηρ)=π2>2. (14)
Следовательно постоянное число геометрически представляет площадь круга с радиусом D. Если начертить круг с радиусом D, поставить в центр круга полюс П и обводным шпилем обвести окружность круга, то при обведении счетное колесо не сделает ни одного оборота. Это произойдет благодаря тому, что плоскость счетного колеса будет всегда перпендикулярна к направлению движения и будет лишь скользить.
Преобразование формулы Р=R 27 для вычислений, Ранее было указано, что при вычислении площэдрй дугу, на которую обернулся ободок счетного колеса, обыкновенно выражают в тысячных долях оборота. Обозначив, как и раньше, окружность ободка счетного колеса через С, 0,001 С через т и число тысячных долрй, на к-рое обернулось колесо при обведении контура фигуры, через μ, получим, что U=т-/г, следовательно Р=R-τ-μ. Там же указано, что число тысячных долей, на которое обернулось колесо, получается как разность т^—т% отсчетов по циферблату, счетному колесу и верньеру до и после обведения контура, следовательно я=m2-n)j и
Р=R -т(т2 -mi). (15)
Множитель Дт есть произведение длины обводного рычага Д на длину 0,001 С и представляет собой площлдь прямоугольника, соответствующую тысячи ой доле оборота колеса, или цену одного деления П. Эту площадь можно рассматривать в ее натуральную величину в см2, миллиметров2 и вообще в тех единицах, в которых выражены Д и т.
Пример. 2? =15,54 см, С =6,18 cjk, 0,001С=т==0,00618 сантиметров (взяты с П. сист. Коради № 22927), следовательно
Дт ~ Ро —16,54×0,00618=0,096 с.м2=9,6 миллиметрови.
Такое значение р„ называют абсолютной ценой одного деления П. Зная эту цену, легко определить натуральную величину площади фигуры в тех единицах, в которых выражено р„. Но ра м. б. придано другое значение. Построим на бумаге прямоугольник р„ по действительным величинам Лит. Построенную площадь будем рассматривать как план некоторого земельного участка, нанесенного в масштабе При составлении плана каждая линия местности уменьшается в М раз; и обратно, чтобы от площади плана перейти к площади земельного участка, нужно ____
линии плана увели- "
чить в Мраз. Увели- s°
чив R и т в Ж раз ям
(фигура 12), получим ф
другое значение для цены деления П., например S„, выраженное в земельной мере. Ее называют относительной ценой одного деления П., следовательно
So=R · т · М (16)
Числовое значениер0 и S0eсть коэф. к ф-лы (13). Подставляя вместо 11 τ в формуле (15)
So
RM ~~ Фигура 12.
ь
численную величину р0 или S„, будем получать площадь или в натуральную ее величину (в см2 или миллиметров2) или в земельной мере (га или м2).
Определение численной величины цены деления П. Заменяя далее в формуле (15) Rt численным значением р0и So, получим две ф-лы:
р=р0(т2 -“,)и?=S0(m2 — mj.
Первая формула выражает площадь в натуральную ее величину, вторая—в единицах земельной меры. Отсюда
Ро =
mo-mi
т2 — т1
следовательно для определения цены деления П. надо знать площадь в соответствующих единицах (р и Р) и соответствующее число делений П. (т2— т,), то есть число тысячных долей оборота счетного колеса. На этом основании цена деления П. проще всего определяется опытным путем: строят на бумаге квадрат со сторонами в несколько сантиметров или дм., смотря по тому, в каких квадратных единицах будет выражаться площадь. Затем этот квадрат обводят несколько раз П. Из разностей отсчетов до и после обведения берут среднее, то есть получаютРазделив площадь квадрата на среднюю разность отсчетов, получают цену одного деления планиметра в натуральных единицах, т. е-B СЛ12 или в дм.2
Пример. Построен квадрат со сторонами в 5 см. Площадь квадрата равна 25 см2 или 2 500 миллиметров2. Средняя разность отсчетов, выведенная из 5 обведений, равна 266 тысячных, или делений П.
25
Ро 266
ем2=0,094 см2=9,4 миллиметров2.
Для определения S0 площадь квадрата надо выразить в земельной мере, принимая во внимание масштаб плана (ф-ла 16). Положим, что масштаб плана ——.
10000
т. e. 1 сантиметров соответствует 100 м, следовательно сторона квадрата будет равна 500 м, а его площадь 250 000 м“ или 25 га. Поэтому
Ь-щ гα= 0,094 гааг0,1 га; S0 =.и2=939,85 м2.
Для увелич ния точности обведение П. делают несколько раз. Отдельные результаты (разности отсчетов) не должны отличаться более, чем на 1—2 деления. В таком-случае за окончательный результат принимают среднее арифметическое. Самое обведение по сторонам квадрата следует делать по линейке (лучше по металлической), чтобы уменьшить сотрясение руки, искажающей отсчеты.
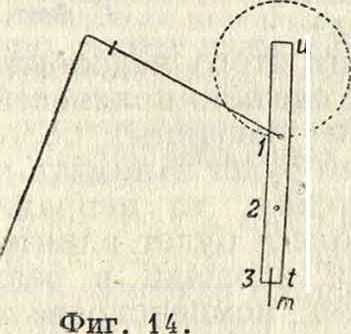
Контрольная линейка. К каждому ГГ. прилагается небольшая линейка, которая помещается в его ящике. Эта линейка· называется контрольной и служит для определения цены деления П. и вообще для его исследования. Контрольная линейка исключает необходимость построения геометрии. фигур для определения цены делений и позволяет быстро определять эту цену, уничтожая при этом сотрясение руки. Здесь описана контрольная линейка, приложенная к П. сист. Коради с постоянным рычагом за № 22927 и рассчитанная для определения цены деления П. для масштабов с прежним основанием (дюймовым). Но зная цену деления для масштаба с одним основанием, ее легко определить и для всякого другого. Контрольная линейка, изображенная на фигуре 13 в плане и в разрезе,—металлическая, хорошо отполированная пластинка, длиной ок. 3,5 дм. Водном ее конце вставлена тонкая игла и, прикрытая винтом v. Другой конец линейки сточен под острие, на котором нарезан штрих t. Место, где вставлена игла и, отмечено нулем. Начиная ют него, через каждый дм. на поверхности линейки высверлены небольшие гнезда, отмеченные 1", 2", 3". Во время работы линейку кладут на бумагу, в которую вдавливают иглу и. У другого конца линейки тонким карандашом проводят на бумаге черту
О
V

“I ~.
Ц Фигура 1j.
ж, с которой совмещают штрих линейки t. В гнездо, отстоящее от иглы на 1", вставляют обводный шпиль, а П. примерно устанавливают так, как показано на фигуре 14, и делают отсчет, а затем, придерживая одной рукой обводный шпиль, чтобы он не вышел из гнезда, другой рукой осторожно двига-,ют контрольную линейку по ходу часовой •стрелки. Обведя полный круг, совмещают
штрих t с чертой т и снова делают отсчет. Т. о. обводный шпиль пройдет по окружности круга с радиусом в 1". Окончив обведение, его надо повторить, но двигая П. уже в обратном направлении, то есть против движения часовой стрелки. Подобным образом обводят круги с установкой обводного шпиля на 2" и на 3". На основании изложенного будем иметь следующие формулы для определения цены деления с помощью контрольной линейки: если S—определяемая цена деления П., mj и ж i—отсчеты до и после обведения круга с радуисом r= 1", т.2 и то/—отсчеты для круга в 2г, то3 и то3 — •отсчеты для круга в Зг, то
S(mi — mj=яг2=яг2,
S(m - тг)=я(2г)2=4яг2,
S(ma — то3)=л(3г)2=9яг2,
•откуда
g, ”·2 4лг2 9 лг“ (Ш)
т -т i ггЦ-т2 та-та 0
В следующей таблице приведены результаты определения цены деления П. сист. Ко-ради с постоянным рычагом № 22927 с установкой на контрольной линейке обводного шпиля на 1, 2 и 3 дм. Цена деления вычислена как для определения натуральной величины площади (в дм.2), так и в земельной мере, старой (в дес.) для масштаба и но-
8 4UU
вой (в га) для масштаба --.
Определение цены деления П. дляразныхмасштабов. Выше при-
| Длина г | т - Ш т2 - тп2m?t m3 | 4πτ2
9лт2 | S | |
| 1 дм. | 212 | 3.1416 Дм.2 | 0,0143 дм.2 | |
| 2 » | 887 | 12,5664 » | 0,0142 » | |
| 3 » | 1968 | 28,2744 » | 0,0143 » | f |
| 100 сж. | 212 | 13,09 дес. | 0,061 дес. | |
| 200 » | 887 | 52,35 » | 0.058 » | *2 |
| 300 » | 1 968 | 117,79 » | 0,059 »> | |
| 254 м | 212 | 20,27 га | 0,095 га | |
| 508 » | 887 | 81,07 » | 0,091 » | Us |
| 762 » | 1 968 | 182,41 » | 0,093 » | f |
Сррдняя S: *1 0,014 дм.2; *2 0,059=0,06 дес.;
0,093=0,09 га.___
ведена ф-ла, выражающая цену деления П. в земельной мере (ф-ла 16): S0=R-r-M2. Из нее видно, что S„ изменяется пропорционально изменению длины обводного рычага R и пропорционально квадрату знаменателя численного масштаба (т изменяться не может). Если измерять площади разных масштабов, но при одной и той же длине рычага R, то S„ будет зависеть только от масштаба. Если новый масштаб то для него цена деления будет S^R-τ-Ν2. Взяв отношение равенства,будем иметь |^= откуда
Si=SoHV (1?)
Эта формула позволяет цену деления, вычисленную для одного какого-либо масштаба, перечислить для произвольного.
Пример 1. Для масштаба g * S0=0,06 дес.
Вычислить Sj и S2 для масштабов и —щ.
Si =0,06
= 0,015 дес.,
S2 =
„ „„ /42 000 2, _
°’°6 ( 840о) =15ДеС·
Из этого примера видно, что знаменатель второго масштаба в 10 раз более знаменателя первого, а цена деления S2 более Si в 100 раз (Ма).
Пример 2. Для масштаба S0=0,06 дес.
Вычислить Si в метрич. мере для масштаба —
Пользуясь соотношением 1 дес.=1,09254 га, сначала надо перевести 0,06 дес. в га. Полученный результат
0,0655524 дает цену деления в га для масштаба
8400
Остается перечислить ее для масштаба
Si
/10000 2
= 0,06555 (g^oj =0,093 га;
получилась та же цена, которая вычислена по контрольной линейке и помещена в предыдущей таблице.
Цена деления П. обыкновенно дается механиком для разных масштабов и при определенной длине обводного рычага. Результаты обычно пишутся на ярлыке, наклеенном внутри футляра П. Так, для П. К» 22927 цены вычисле! ы для й=309,0 полумилли-метров. Цена деления м. б. вычислена непосредственно по формуле S0=R-r· М2, если известны размеры П. Так, для планиметра № 22927 при R=6,16 дм. <7=2,42 дм. и М=8 400, τ =0,00242 дм.; М2=70 560 000 и&„==6,16x0,00242x70 560 000=1 051 852 дм.2 По обращении в дес. S0=0,0G2=.0,06 дес.
Вычиелениевесьмамалыхпло-щ а д е й. При вычислении малых площадей большая цена деления дает и больший процент ошибки, поэтому выгоднее в таком случае, чтобы цена деления была возможно меньшей, а разность отсчетов μ^ — μ, возможно большей. Но р0 =ϋτ, следовательно для уменьшения р0 надо уменьшить R. Если при длине рычага R цена деления была р„, то для новой цены рг рычаг надо изменить в Rx:
p0=R-T, Ρχ^Ρχ-τ;
взяв отношение, будем иметь ~ · Из этой пропорции получим
Ρο-Pi Д-Д1 Ро л откуда R—=R · р°~р“. По этой формуле вычисляется изменение длины рычага при изменении цены деления в другое.
Вычисление постоянного числа. При постановке полюса внутри фигуры ее площадь вычисляется по ф-ле: Р= RU + Q или P=S0(m2 - mi) + Q. Если q—число делений П., соответствующее площади круга Q (So—цена одного деления П.), то предыдущая формула представится так: Р =So(m2 —mi) +S0Q, откуда
1=ζ·~ (m» - mi).
*0
p
В этом выражении ^--площадь фигуры в делениях
Ьо
П„ a (ma-mx)—разность отсчетов до П., когда его нолюс внутри фигуры.
Пример. Для определения q взят квадрат со сторонами в 30 см; масштаб чертежа следова тельно сторона квадрата равна 3 000 м, а его площадь
Р 900
900 га. Цена деления П. S0 =0,09 га, член—=—==
оо 0,09
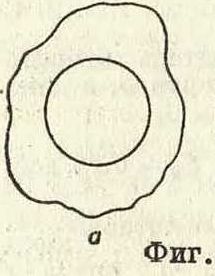
= 10 000 делений. Разность отсчетов по П. m2-mi до и после обведения квадрата в среднем из 4 обведений равна 9 347, следовательно q=10 000 — (— 9 347)=19 347 делений. Появление отрицательного знака у разности m2-mi объясняется тем, что площадь вычисляемого квадрата Р менее площади круга Q. В этом случае счетное колесо при об-
© в едении П. будет вращаться в обратную сторону, мимо нуля верньера, подпись колеса будет проходить убывая, и второй отсчет т2 будет менее первого mi. Действительно, в формуле 6 P =RU + Q, где все чле-
15· ны положительны, Q
входит слагаемым. Разность P—Q =RU будет положительна и соответствует пространству между кругом Q и контуром (фигура 15,а) к-рое П. обращает в прямоугольник RU. Если Q более Р, то P - Q=-RU. Но R отрицательным быть не может, и отрицательным будет U, т. e. m2 —mi, и тогда mi>m2. Отрицательное RU соответствует пространству между кругом и контуром на фигуре 15 б. Для получения численного значения - RU надо обводить П. против хода часовой стрелки; в этом случае счетное колесо будет вращаться по возрастающей подписи, и второй отсчет т2 будет более первого mi. Приведенную выше формулу P =S0(m2-mi)-fS0q можно переписать так:
Р=S0[(m2 + q)- mi];
из нее видно, что при вычислении площади с постановкой полюса внутри фигуры надо ко второму отсчету прибавить число делений, соответствующее постоянному числу. Постоянное число в делениях П. также дается механиком для нек-рых масштабов и при определенной длине обводного рычага. Соответствующие числа написаны на ярлыке, наклеенном в футляре П.
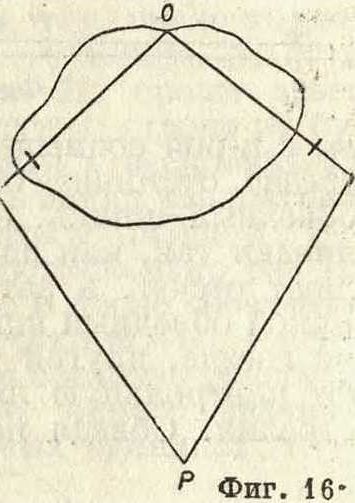
Условия, требуемые от П., них поверка. Условия, требуемые от П., следующие: 1) счетное колесо должно свободно вращаться; 2) плоскость счетного колеса Д. б. перпендикулярна к направлению обводного рычага; 3) длина обводного рычага должна соответствовать цене деления П., которая дана механиком; 4) постоянное число должен быть вычислено правильно. При исследовании 1-го условия вращают счетное колесо около оси. Если вращение медленное, колесо будет останавливаться—ось слишком зажата. В этом случае положение оси надо изменить, действуя винтами при подшипниках. При вывинчивании подшипники будут раздвигаться, и вращение оси будет свободнее. При очень быстром вращении подшипники, наоборот, надо сдвинуть. При этом необходимо обратить внимание на то, чтобы счетное колесо не задевало верньера. Поверка 2-го условия, самого важного, производится так: измеряется площадь фигуры при двух положениях П., к-рый устанавливают так, как показано на фигуре 16, то есть счетное колесо в первый раз будет находиться влево, а во второй—вправо от линии, соединяющей полюс и обводный шпиль (линия РО). При обведении фигуры при обоих положениях П. делаются отсчеты, а их разности сравниваются между собой. Если разности отсчетов будут значительно различаться, то условие перпендикулярности не выполнено. Для исправления этого недостатка в П. системы Коради не сделано приспособлений. Но так как при указанных положениях П. счетное колесо будет занимать противоположные положения, то неправильность в положении колеса будет влиять на результат вычисления площади в разных направлениях и будет компенсироваться. Вследствие этого П. сист. Коради называют компенсационным. На этом основании можно рекомендовать производить вычисление площади при двух указанных положениях П. Среднее из результатов будет почти свободно от влияния этой ошибки. Поверка 3-го условия производится так. обр.: при помощи контрольной линейки вычисляется площадь круга. При этом свободный рычаг П. устанавливается на длину, указанную механиком. Обведение круга делается при двух положениях инструмента, указанных на фигуре 16. Для увеличения точности такое обведение следует повторить. Если разности отсчетов будут отличаться на 1—2 деления, то за окончательный результат принимают среднее. Умножив эту разность на цену деления П. S0, данную механиком и соответствующую длине рычага, получают площадь круга по формуле P=S0(m2- тх). Затем, вычислив площадь того же круга по формуле да2, сравнивают с ней площадь, вычисленную П. Если площадь по П. будет более площади, вычисленной по формуле да2, то рычаг надо удлинить; если менее, то надо уменьшить. Это следует из того, что для одной и той же площади RV— R1U1, то есть длины обводного рычага обратно пропорциональны длинам дуг, на которые обернулось счетное колесо. Следовательно для уменьшения длины дуги или соответствующей ей площади надо уве-
личить рычаг и наоборот. Изменение длины рычага м. б. рассчитано по ф-ле
R1-R=R,‘^;
1 И1 ’
здесь μ—число делений, вычисленное для круга по формуле а и±—разность отсчетов по П. при установке его на длину рычага R.
ПГ%
Пример. К=332,1 полумиллиметра, /i=-=-=2 088
Ьо делениям, μ, =2 108 делениям, Ri - R=332,1 ·——=
105
= 3,16 — 3,2 полумиллиметра. Т. к. площадь по планиметру оказалась более геометрической, то рычаг надо увеличить, и J?1=335,B полумиллиметра. Установив рычаг на новую длину, надо повторить испытание. Поверка постоянного, числа, вернее, числа делений q, соответствующего площади круга Q, производится так, как описано выше.
Некоторые замечания о пользовании Π. 1) Надежные результаты П. дает, когда вычисляемая площадь начерчена на ровной, гладкой бумаге, без всяких шероховатостей. Неровная бумага влияет на обороты счетного колеса и искажает отсчеты. 2) Не следует делать начальный отсчет нулем, а лучше записать его так, как указывает инструмент. При установке на нуль можно не заметить 1—2 делений, на которые отойдет счетное колесо. 3) Когда указатель на циферблате находится близ какой-либо цифры, то надо обратить внимание на положение нуля верньера относительно штрихов счетного колеса, подписанных 9 (девяткой), 0 (нулем) и 1 (единицей). Если нуль верньера находится между 9 и 0 колеса, то с циферблата надо взять меньшую цифру; если он находится между 0 и 1, то надо записать ту, на к-рую указывает индекс. 4) Обводный шпиль надо двигать по контуру осторожно, выбирая все извилины, следя в то же время ва движением циферблата. Если при обведении контура по ходу часовой стрелки нуль циферблата прошел мимо указателя несколько раз, то столько же раз ко второму отсчету прибавляется 10 000; при обратном движении эта цифра вычитается. 5) Обведение контура надо делать не менее двух раз в прямом и обратном направлениях и при двух положениях планиметра. 6) При вычислении малых площадей выгоднее брать рычаг короче.
Точность вычисления площадей П. зависит от многих условий. На нее влияет качество плана, форма контура, величина площади и прочие Изменение площадей по старым планам, бумага которых измята, менее надежно. Также невыгодно вычислять П. узкие и длинные полосы, дороги, просеки, канавы, лесные делянки и прочие Площади таких полос точнее вычислять по натуральным измерениям. Малые площади вычисляются с большей ошибкой. Практика показывает, что при наивыгоднейших условиях измерение площадей П. сист. Коради при двух положениях инструмента производится с ошибкой до 0,0025 или (—) изме-
400
ряемой площади. Механик Коради ввел усовершенствование в своем компенсационном П., поместив счетное колесо на особую шайбу, сделанную из твердого каучука и
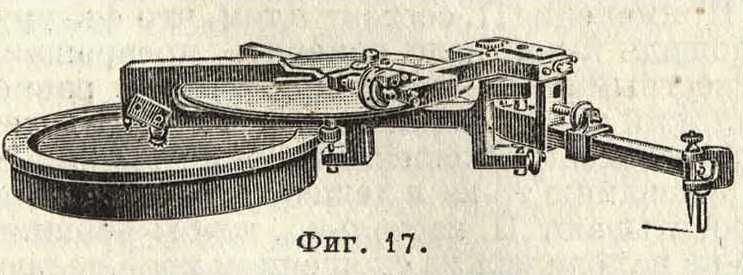
гладко отполированную; благодаря этому на отсчетах по колесу не сказываются неровности бумаги (фигура 17). С. Цветков.
Б. Наиболее совершенным из линейных П. является линейный П. с шаровым сегментом сист. Гомана·—Коради (фигура 18). Он состоит из рамы АА, в которой вращается ось с наглухо приделанными к ней двумя тяжелыми валиками ВВ равных диаметров, так что при передвижении прибора по бумаге он сохраняет неизменное направление. Параллельно оси валиков ВВ в верхней части рамы расположена другая ось с зубчатым колесиком и тщательно выточенным шаровым сегментом е, прикасающимся к совершенно гладкому полированому цилинд
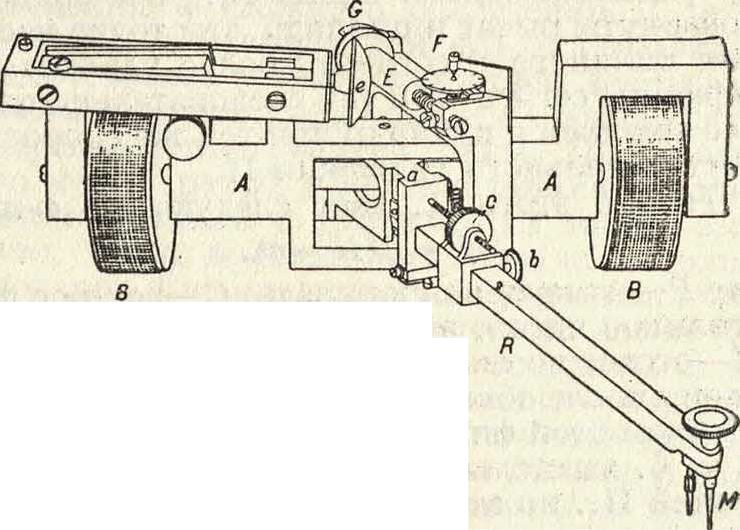
Фигура 18.
ру Е, целые обороты которого отсчитываются на циферблате F, а части оборота по верньеру на барабане G. Наружные поверхности валиков ВВ нарезаны мелкими зубцами (насечками), так что валики moijt только катиться, но не скользить по бумаге; зубцы левого валика В захватывают зубцы зубчатого колеса оси вращения сегмента е, и потому во время движения прибора на бумаге вращаются как валики ВВ, так и ось сегмента е; соприкасаясь с поверхностью цилиндра Е, шаровой сегмент е вращает цилиндр Е. Если зубцы валиков и зубчатого колеса оси сегмента е одинаковы, то длина дуги, на к-рую обернется валик В, равна общей длине дуги всех одновременных оборотов оси сегмента е; иначе говоря, линейное-перемещение всего прибора по направлению, перпендикулярному к оси валиков ВВ, равно линейному перемещению какой-либо· точки окружности оси сечения е. В середине рамы АА расположена вертикальная ось, около которой может поворачиваться вправо и влево в известных пределах обоймица а; в верхней части этой обоймицы помещен упомянутый выше гладкий цилиндр Е, а внизу вставлен длинный брусок R (рычаг), с ведущим острием М на конце. Брусок разделен по всей своей длине на миллиметров и при помощи небольшой обоймицы с верньером, зажимным винтом Ь и гайкой с м. б. поставлен и закреплен в любой части своей длины, для чего он вдвигается в обоймицу или выдвигается из нее. Ведущее острие М составляет третью точку опоры инструмента во время измерения площади; но две другие· точки опоры (валики ВБ) расположены так, что ц. т. всей системы находится почти над ними и давление на ведущее остриеЖ незначительно. Оси цилиндра Е и бруска (рычага) R всегда параллельны, причем цилиндр Е особой пружиною в обоймице постоянно нажимается на шаровой сегмент е и, смотря по положению обоймицы а, зависящей от движения ведущего острия вправо или влево, касается сегмента в разных точках. Когда ось рычага R перпендикулярна к оси валиков ВВ, тогда цилиндр Е касается вершины сегмента и остается неподвижным, хотя бы П. двигался и сегмент вращался.
Если рычаг повернуть вправо, то цилиндр Е касается сегмента в точке, расположенной ближе к барабану G, и при движении П. ^вперед вращается в сторону возрастающих надписей циферблата и барабана; наоборот, если рычаг R повернуть влево, то цилиндр .Е коснется сегмента в точке, более удаленной от барабана G, и при том же направлении движения П. будет вращаться в сторону уменьшающихся надписей. Чем больше повернуты рычаг и цилиндр, тем точка касания цилиндра к сегменту более удалена от вершины сегмента, и тем следовательно скорее вращается цилиндр при той же скорости поступательного движения П.
Теория этого П. дает следующую ф-лу: Р=C(N - п),
где Р—измеряемая площадь, С—пек-рое постоянное число, зависящее от размеров П., N—отсчет по циферблату, барабану и верньеру после обвода фигуры, п—отсчет перед •обводом этой фигуры. Постоянная величина € м. б. вычислена по измерению отдельных частей П., но это не точно; точнее и скорее определить ее из опыта, обводом какой-нибудь простой геометрич. фигуры известной площади, например круга или квадрата. Зная площадь такой фигуры и отсчеты при начале и конце обвода, получим:
° N-n
Постоянную С можно изменить, вдвигая и выдвигая рычаг R. Для широких площадей можно вставить дополнительное колено. Т. к. рычаг и дополнительное его колено имеют мелкие деления, то, определив С при двух разных установках (длинах) рычага, можно вычислить по пропорции ту установку, при которой постоянная С’ будет круглым числом или числом, выражающим площадь в м2 или в других мерах при данном масштабе плана (чертежа).
Для измерения площади описанным II. ставят его на чертеж так, чтобы ось валиков В В приняла направление, перпендикулярное к длинной средней линии обводимой фигуры, и чтобы отклонения рычага с ведущим острием в ту и другую стороны были достаточны для обвода по всем извилинам контура. Затем, установив острие М в любую точку контура, отмечаемую наколом тонкой ;иглы или же тонко очиненного карандаша, .делают отсчет по циферблату, барабану и язерньеру; после этого обводят контур острижем в сторону вращения часовой стрелки, пока острие не вернется в начальную замеченную точку, и делают второй отсчет. Разность отсчетов, помноженная на постоянное число, даст площадь обведенной фигуры ® мелких или земельных мерах.
К линейным П. можно отнести л и н е й-ку-плаыиметр Зарубина (фигура 19: А—профиль, Б—план). Она состоит из двух частей: линейки и счетного механизма. Линейка LL имеет на обоих своих концах по прямоугольному вырезу тп, в которых вращаются на общей оси 00 два одинакового диаметра валика а с рубчатой поверхностью. Концы оси помещаются в стойках К и К, которые привинчены к линейке; для уменьшения трения в концы оси 00 (в ко нические в них углубления) входят конические острия, вделанные в стойки К и К и составляющие с ними одно целое. Для удобства прокатывания линейки по бумаге, на которой начерчен контур, на ее концах сделаны две рукоятки д, д. Сверху ось и валик

т п т л
Б

Фигура 19.
прикрыты полым медным полуцилиндром D. Счетный механизм (фигура 20: А—вертикальный разрез, Б—план) устроен след, образом: конец b оси валиков аа снабжен шестерней е, передающей своими зубцами вращательное движение зубчатому коронному колесу р, соединенному наглухо с его вертикальною осью вращения, утвержденной нижним концом в линейке, а в средней части в стойке-скобе, снизу привинченной к линейке. На верхний конец оси коронного колеса насажена большая стрелка б, вращающаяся по большому внешнему кругу
Д Б
| б м | 0
) ® | |
Фигура 20.
циферблата Z. Для подсчета полных оборотов большой стрелки б над циферблатом имеется другая, малая стрелка ж, движущаяся по внутреннему кругу, концентрическому с первым. Внешний круг разделен на 100 частей, подпись идет слева направо через каждые 10 делений; внутренний круг имеет 50 делений. Малая стрелка движется в 50 раз медленней большой, что достигается системою зубчатых колес, передающей движение большой стрелки б малой стрелке м. Вследствие равенства диаметров валиков скошенный край линейки L при движении планиметра перемещается параллельно самому себе. Из устройства П. ясно, что число оборотов валиков, помноженное на длину окружности валика, выражает длину пути, пройденного П. по бумаге.
Применение П. состоит в том, что фигуру, площадь которой надо измерить, превращают известными геометрич. приемами в равновеликий треугольник (или трапецию); затем прикладывают скошенный край линейки П. к основанию тр-ка и делают отсчет и; затем прокатывают П. настолько, чтобы вершина тр-ка находилась на скошенном крае, делают второй отсчет п разность отсчетов п-п, помноженная на длину окружности валика, выраженную в тех или иных мерах длины, даст длину высоты тр-ка, следовательно и половину ее длины; помножив половину высоты на длину основания, получим площадь тр-ка, равновеликого площади фигуры. Для удобства применения П. на скошенном краю линейки наносят единичное основа-н и е. Полученный равновеликий тр-к с произвольным основанием приводят (геометрии. приемом) к тр-ку с единичным основанием. Если прокатить П. от единичного основания тр-ка до его вершины, то полу-разность отсчетов, помноженная на длину окружности валика, дает площадь тр-ка в •соответствующих мелких или земельных мерах. Вместо первого отсчета можно перед прокатыванием П. ставить стрелки на нули: тогда отсчет после прокатывания определит длину высоты тр-ка с единичным основанием. Площади измеряются линейкой-П. системы Зарубина с точностью ±0,01 измеряемой площади.
К оригинальным по мысли П. можно отнести: 1) П. Вебера-Керна и 2) П.-топорик Прнтца. П. Вебера-Керна (фигура 21) состоит из двух рычагов—переменного по длине, обводного рычага с острием А и счетного рычага В; рычаги скреплены под прямым углом и имеют цилиндрич. поверхность.
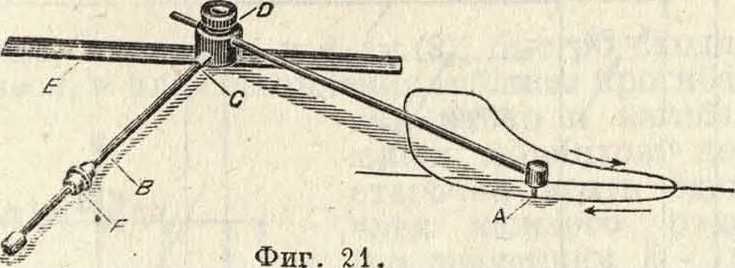
lB вершине прямого угла помещена тяжесть D с острием (иглой), скользящим в продольном ^прямолинейном жолобе неподвижной .линейки Е. На счетном рычаге нанесены миллиметровые деления и на него надета колесо-муфта F с зубчатым лезвием (краем) инеболыним верньером, скользящим вместе ►с колесом вдоль по счетному рычагу; точность верньера 0,2 миллиметров. Неподвижная линейка имеет на нижней поверхности две иглы, которыми она прикалывается к столу. Теория этого П. дает формулу P=R-a, где Р— измеряемая площадь, R—длина обводного рьшага, а—путь, пройденный колесом-муфтой по счетному рычагу. Применение этого П. состоит в следующем: устанавливают обводный рычаг AD на какую-либо заранее намеченную длину, например 20 см, отмеченную на рычаге штрихом с надписью, вдвигая и выдвигая его в отверстие тяжести в вершине угла; вставляют счетный рычаг В его расщепленным концом С в отверстие тяжести Ώ делениями вверх; укладывают линейку на чертеж так, чтобы контур измеряемой площади можно было удобно обвести вокруг, то есть без того чтобы игла тяжести Ώ могла выскакивать из паза (желобка) линейки Е затем обводят по контуру слева направо. Перед обводом надо проте-ретьсчетный рычаг сухою тряпкою, чтобы ко-.лесо-муфта скользило свободно. По окончании обвода отсчитывают длину а пути, к-рый проскользила муфта по рычагу; произведение длины а на длину R обводного рычага дает искомую площадь в, мелких или земельных единицах.
П.-топорик Притца—см. Интегрирующие приборы.
Т. 9. m. XVI.
Лит.: Соловьев С. М., Курс низшей геодезии М., 1914; В итковск и и В. В., Топография, 3 изд.! М., 1929; Бик А. Н. и Чеботарев А. С., Учебник низшей геодезии, 9 изд., М.—Л., 1928;×в о л ь-сон О. Д., Курс физики, т. 1, стр. 250—252, Берлин, 1923. М. Бонч-Бруевич.