> Техника, страница 71 > Пластины

Пластины

Пластины, пластинки, плиты, тела, имеющие форму прямого цилиндра или призмы с малой по сравнению с размерами основания высотой; в строительной технике—главным образом тонкая плита, подверженная изгибу.

Диференци альное уравнение равновесия П. постоянной толщины. Плоскость, параллельную основаниям цилиндра или призмы и делящую высоту пополам, называют срединной плоскостью П. Относим П. к прямоугольной декартовой системе координат. Располагаем оси ж-ов и ?/-ов в срединной плоскости; ось z направляем перпендикулярно к этой плоскости. Через да обозначаем прогиб срединной плоскости (да называют упругой поверхностью П.), а через и и v—перемещения, соответственно параллельные осямж-ов и у-ов. При выводе ур-ия поверхности, вид которой принимает срединная плоскость, принимают, что последняя не испытывает растяжений, что линейные элементы, перпендикулярные к срединной плоскости, после изгиба нормальны к срединной поверхности, что при изгибе П. точки срединной плоскости перемещаются только параллельно оси

2-ов, то есть для точек этой плоскости перемещения и=v=0, что толщина П. h бесконечно мала по сравнению с ее размерами, а прогиб да мал по сравнению с h. Удлинениями линейных элементов срединной плоскости пренебрегают как бесконечно малыми высшего порядка по сравнению с такими удлинениями для слоев П., удаленных от срединной плоскости. При вычислении нормальных напряжений Х_х, Y_y и касательных Y_x для данного напряжённого состоя-

18

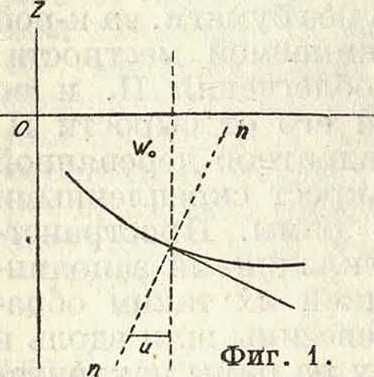
ния пренебрегают величиной нормальных напряжений Z_z, вызываемых непосредственным дейстпием нагрузки на П., как величиной малой по сравнению с напряжениями Х_х и Y_y в удаленных от срединной плоскости слоях И. Кривая на фигуре 1 представляет след от пересечения срединной плоскости в изог нутой II. с некоторой плоскостью, параллельной осям ж-ов и г-ов; w—перемещение некоторой точки срединной плоскости. Перемещение и нек-рого эле мента, отстоящего от срединной плоскости на расстояний z, выражается аналитически первым из следующих двух равенств:

dw ди>.

^{U =} ~ ^ZT)x ’ ^V ~~ ^Z~dy’ таким же образом получается перемещение v из сечения пластины параллельно плоскости осей у-ов и г-ов.

Деформации:

_ ди _ 9²w _ 9υ__9²w

^е« ^_ дх ~ ~ ^Z to² ’ ^еУУ~ ду~ ^Z 9у² Пренебрегая влиянием Z_z по сравнению с напряжениями Х_х и Y_y, можно написать:

d²w 1 -v -v

~^Z дх“~~Ё^^х

_ 9²W 1 „γ ,.

# я.9. - Τ7 ^Χ_χ),

дуг откуда:

9²w ^σ дуг)’

у. Ez /9²w

"** 1-σ² .9x²

V ^Εζ (^a*^w I „0ЧЛ

^XV~ ι-σ·ζ [дуг ^σ дх“

(1)

(2)

Через а обозначен коэф. Пуассона. Касательное напряжение:

v - г (ЁИ л.=- 9Г * -^w=_ ^{Ez ж} 19у 9х 9х9у 1 + 0 9ж9у

Из ур-ий равновесия дХх, 9Г_Ж βΧ_ζдх ду dz

О и дУх дх

^dYy I ₌ о ду ^ dz

получим:

dX_{z =} _Ez_ (d³v> 9³w

dz ~ 1 - σ² V θχ³ 9х9у²j Ez (9³w

9X

dz

9Zj

9z

9x9y² 9³u>

σ² 9y³ 9x²9y)

T. к. при 2=± ^ (h—толщина П.) X_z=Z^=0,

из последней ф-лы путем интегрирования по 2 получим (удовлетворяя поставленным условиям):

_ _ E(ft²-4z²) (9³w, 9³w

8(1 —σ²) I9x³"^"9x9y ^ E(ft²-4z²) /9³w 9’»

^ 8(1 —o²) ^ 9y³ + 9y9x²

Если обозначим сумму перерезывающих сил на единицу длины в сечении, перпендикулярном оси ж-ов, через V _xz и такую же сумму в сечении, перпендикуляр ном^ оси у-ов, через V_yz, то + Λ/2

Е№, д³ к>

V„=f X, dz=-

-h/2

12(1-σ²) 5α:³ доеду¹

+ :

S) w

Eh³

d³iv

+ b/2

+ <⁴>

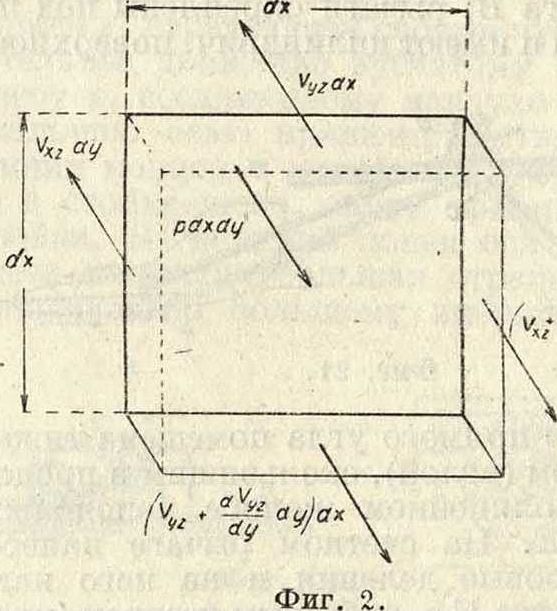
Вырежем элемент П. плоскостями х, ж-+ г/ж, У, У + dy приложим действующие на этот элемент напряжения; элемент должен быть в равновесии. Проектируя силы на ось 2-ов (фигура 2),. получим:

’ +

дУ_Уг

9V

дх "и ду или (по Лагранжу):

Eh³ /d⁴w, ₀ d⁴-w

+ 2

__, 9»w

9х²9у² 9yV

(5>

12(1 — сг2) дх4

гле р—нагрузка на единицу площади, за-висящая от ж и у и действующая нормально“ к срединной плоскости П., w должно удовлетворять ур-ию (5) и пограничным усло-

**) зу·

виям. Изгибающий м ом ент на единицу дли- -ны в сечении плоскостью, перпендикулярной к оси ж-ов (вращает около оси у-ов):

+ д/2

ш(в + ·»)· <«>

- h/2

Изгибающий момент на единицу длины в-· сечении плоскостью, перпендикулярной к оси у-ов (вращает около оси ж-ов):

+ Λ/2

^м“~,

/2

Свободно опертая прямоугольная П. При равномерно распределенной нагрузке выражение для w может быть, взято (по Галеркину) в сл. виде (фигура 3):.

^р(1_яа) {16ж⁴ - 24а²ж² + 5а⁴ -

+ Λ/2 — Τι/2

1536а⁴

B2Eh^d

оо (-l)bx ch^-^CS ^(2fe"¹⁾^^C

2

i

(2fe-l)5ch

(2k — t)nb 2а

192(/>-2y)a³v|^{( 1)4+1 Sh} я“ X

(2fe-l)(b+2i/)

2a

(8>

(2fe -1) лзс

(2fe — l)⁴ Cll²

(2/i - 1)лЬ 2a

_192(Ь+2у)а³>

, /_n sh (2fe-lMb-2y) _cg (2fe - 1)πχ Ί 2 a

(2ft —l)⁴cb²

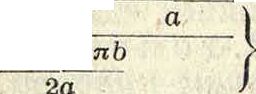
(2fe — 1 j

где а — ширина, Ь — длина П. По ф-лам (6) и (7) могут быть определены изгибающие моменты. Приводим в таблице 1 значения для М_у и М_х при α= 0,25.

Таблица I .—И вгибающие моменты при

=0,25.

1	2	3	4	б	6	7	8
	•w	Му (в	pa2) в точках:		Мх (в	pa2) в точках:
	(в pat)		зс=0;	а	я=0;	х=0;	а
а	г Eft3;		а	х= ;	У=0	b
	в центре	У—0	У=4	У=0		У=4	у=0
1	0,0457	0,0460	0,0340	0,0378	0,0460	0.0378	0,0340
1,1	0,0546	0,0535	0,0399	0.0432	0,0472	0,0395	0,0347
1,2	0,0635	0,0609	0,0456	0,0484	0,0475	0.0403	0.0349
1,3	0,0718	0,0677	0,0508	0,0532	0.0474	0.0411	0,0349
1,4	0,0793	0.0738	0,0557	0,0577	0,0472	0.0417	0,0345
1,5	0,0868	0,0798	0,0606	0,0617	0.0462	0,0410	0,0340
1,6	0,0934	0,0849	0,0650	0,0654	0.0454	0.04J1	0,0334
1,7	0,0994	0.0896	0,0692	0,0687	0,0444	0,0422	0,0328
1,8	0,1047	0,0938	0,0726	0,0717	0,0436	0,04?3	0,0321
1,9	0,1096	0,0975	0.0763	0,0743	0,0425	0,0420	0,0314
2,0	0,1139	0,1008	0,0795	0-0766	0.0415	0.0419	0.0307
3,0	0,1376	0,1186	01016	0,0892	0,0345	0,0392	0.0259
4,0	0,1442	0,1234	0.1128	0,0926	0,0322	0.0365	0,0242
5,0	0,1459	0,1246	0,1187	0,0935	0,0315	0,0344	0 0236
со	0,1465	0,1250	0,1250	0,0937	0,0312	0,0312	0,0234

Ряды, входящие в формулу (8), быстро сходящиеся, и для составления таблицы прогиба, как равно и изгибающих моментов, достаточно взять один член каждого ряда (со значением к=1). Отметим здесь, что w поф-ле (8) удовлетво-__х ряет ур-ию (5) и на

i

х=±

Фигура 3.

контуре (при а равно при у=± ~)

обращается в нуль, кроме того изгибающие моменты М„ и М_тна контуре обращаются в нуль. Для гру за Р, сосредоточенного в центре, величина w определяется следующим выражением:

w=

6Ρα²(1-σ²)

со cs

(2k-l)nx

sh

(2k - )л(Ь—2у)

2 a

(2ft ly l(₂fe-l):rCh

(2k-l )nb

2a

ch

ch

(2k — i)n(b — 2y) ^

²⁰ ch^{2 (2k}-

1 )nb

ch

(aft-i) nb

(9)

2a 2a

Ф-ла справедлива для у5= 0.

П. прямоугольная, закрепленная по всему контуру. Если начало координат взять в центре, w должно обра титься в нуль при х

Ь ______dw

как равно и при у=± -, кроме того при х=±,

dvf

Hfc при у=± ~ должны обратиться в нуль. Решение значительно сложнее, чем для свободно опертой П. В табл. 2 приведены значения изгибающих моментов для равномерно распределенной нагрузки при σ=0,25.

Безбалочные п ок р ы-т и я. Под этим названием понимается обыкновенно плита, опертая на колонны, центры которых расположены в вершинах прямоугольников (все покрытие таким образом разбито как бы на прямоугольники).

Треугольные П. Точное решение для П. в виде ра-внокатетного прямоугольного треугольника (фигура 4) получено для случая, когда П. свободно оперта, то есть когда прогиб на контуре и нормальные напряжения Х_х при ж=0, Y_y при=0, а равно Х_х при х + у — — а= 0 обращаются внутрь. Для равномерно распределенной нагрузки

_w _ ρα⁴(1-σ²) I (зс+y-a)⁴ + 2п(х+у-аУ-а³(х+у-а)

8Eh³

a⁴

_ 96 χΐ

π⁴ Ζλ

(2k

1 ,1^ (2k — 1)π

-T),+ 2^Cth-2-

sn

(2ft -

(2 ft

1)πχ

-1У sh

+ sh

(2ft -1)я 2

-1 )π(α-

(sh

(2h-l)n(a-2y) 2 a

(2k

2x)

sn

+

ΣΓ—

[(2ft-

• sn

l)⁴ sh (2k-l)nx

(2k-l)n a

2

a- 2x

a-2y

ch

(2k-l)nyJI

(2k-l)n(a-2y) 2a

-b^-^ch

a

(2k-i)7ty

(2k-l)n(a-2x)

2a

₍₁₀₎

Таблица 2.—И вгибающие моменты для равномерно распределенной нагрузки при σ=0,25.

b а	Прогиб w в центре (*=0, У=0)	Изгибающие моменты в центре (х=у=0)		Изгибающие моменты на опорах
				Му а при х= -, У=0	Мх при х=0, b У=2
		Му	М,
	pa4 Ж*	:pa2	раз	ра2	ра 2
1 1,1 1,2 1.3 1.4 1.5	0,0143 0,0170 0,0200 0,0216 0,0234 0,0248	0,0220 0,0258 0,0293 0,0321 0,0344 0,0363	0.0220 0,0223 0,0219 0,0210 0,0199 0,0187	-0,0517 -0,0554 -0,0612 -0,0668 -0,0714 -0,0753	-0,0517 -0,0491 -0,0504 -0,0508 -0,0511 -0,0515

Втябл. 3 приведены прогибы и моменты М_у. и М_х. по оси симметрии (при х=у).

Таблица 3,—Прогибы и моменты М_у. и М_х- по оси симметрии.

	II » II о	а У=*=8	а у=х = 4	3 ν-*-ββ
w.. . мх·.	0 (-0,0191+0,0191ог)ра2 (0,0191-0,0191о)ра2	0,0055 bh·1 (-0,0039+ 0,0177а)ра2 (0,0177 - 0,0039<Цра2	„ ρα4(1-σ2) °’0104 Eh* (0,0140+0,0№σ)ρα2 (0,0138+ 0,0140σ)ρα2	ρα4(1 -cr2) 0,0085- * L· ηΛ (0,0186+0,0074σ)ρα2 (0,0074 + 0,0186σ)ρα2

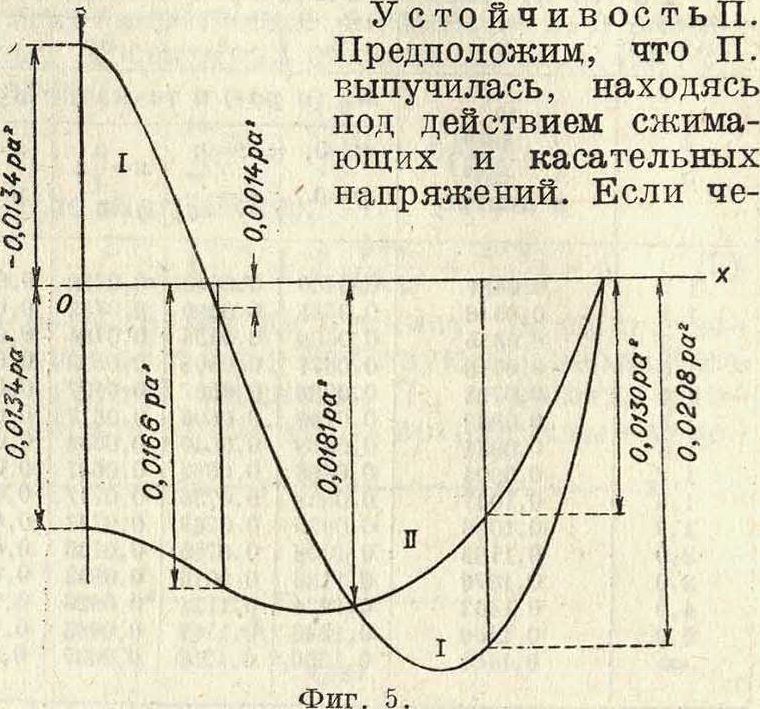
На фигуре 5 приведена эпюра изгибающих моментов М_у, (кривая 1) и М_х- (кривая II) по сечению ж — у=0 при в=0,3. Круглые П. Ур-ие (5) в полярных ци линдрических координатах влено в виде:

Eh³ да м. б. предста-

12(1

1⁽

___1 1 _ э., 1 _8f

-a^z) dr* ‘ г дт г² дв²)

(11)

/3²w, 18w, 1 9²w _

V ,tr· r dr "" г² Э8² ) ~ Ρ·

Когда w не зависит от угла Θ (при симметричной относительно центра нагрузке),

Зр (I-®²)

W =

(г⁴ + Аг² + В In г Б).

WEh³

+ О² In г + Б). (12)

Произвольные коэфициенты А, В, С и Б определяются из пограничных условий. Для П. с закрепленным; краем

3ρ(1-σ²) (_α2_ _Г2)2_ (13)

^W l&Eh³

Для П. свободно опертой

3ρ(1-σ2)

W=-

1бЕ/гЗ

-[(а² - г²)²

4а²(а²-)·²)

“ 1+о~

]· (14)

В формулах (13) и (14) через а обозначен радиус окружности контура. Изгибающие моменты вычисляются для общего случая по формулам:

Мд=—

М_г=-

П. в

Общее

i2(i-o2)Lar2 Eh*

*4~ ^σ ( /1, 1

r dr ^ r²

1 dvo r dr

+

1 02-W 1*2

12(1-σ2)

виде кругового

Э]> (!5)

(16)

решение П.,

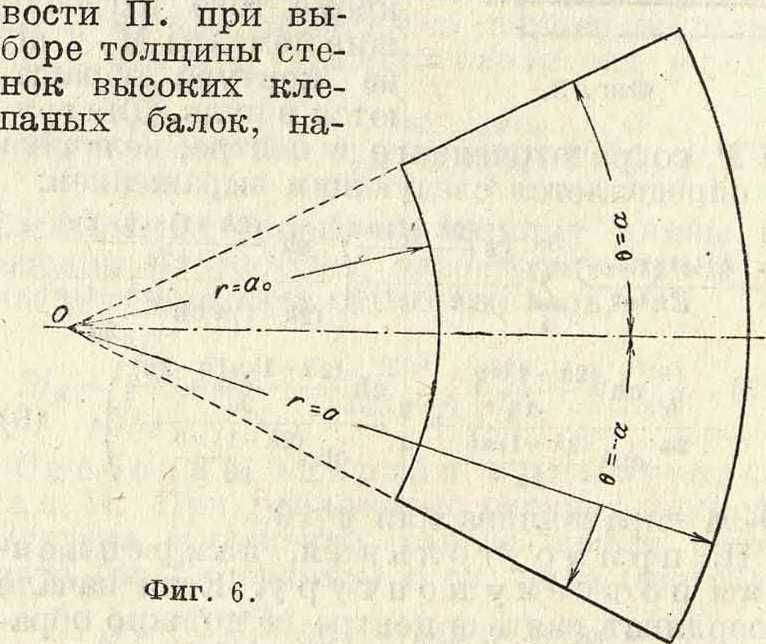
сектора. ограниченной дугами двух концентрических кругов (г=а₀ и г=а) и двумя радиусами (Θ=а и Θ=— — а), для случая, когда по радиальным опорам пластина свободно оперта, дуговые же опоры какие угодно, будет следующее (по Галеркину, фигура 6):

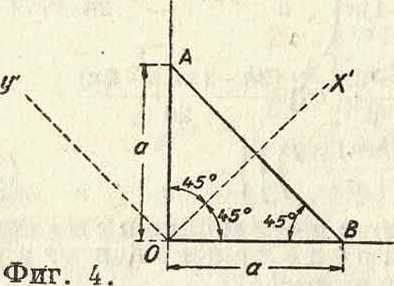
Кг, Θ)

-2

1

В „Г

ηπ

~2α

АУ^а+В_пг ^га + С_пг

Ππ

2а

ηπ + 4а 2а^-

2а

sm

ηπ(α + θ)

2 а ’

+

(17)

где f(r, Θ) удовлетворяет ур-ию

Eh3 i	Э2.
12 (1 —σ2)	Qr2 *

13,1

г dr г²

(ду, i э _ι дч I Зг² г Зг· “1" г² 982

)-

р;

здесь р— нагрузка на единицу площади. Ф-ию /(г, Θ) надо подобрать так, чтобы на опорах θ=α и Θ=— а Ф-ИЯ f(r, Θ) и обращались в нуль. Коэфициенты А_п, В_п, С_пи В_п определяются из условий на дуговых опорах.

Эллиптическая П. Для эллиптической П., равномерно нагруженной и закрепленной по контуру (по Бриану),

^3ρα1Μ -(i-,аз)

W =

2£W(3a-i+2a2b24-3i)i

Колебания П. Диференциальное уравнение для поперечных колебаний П.:

Eh* /9⁴w. ₀ 9⁴w 9⁴w 3²w. .η.

12(1 -а³) дх“~ ^ά дх³ду^{3 +}Ifyi) ~ ^SdW’

здесь ρ—плотность, 7i—толщина пластины.

рез обозначим нормальное напряжение по площадкам, перпендикулярным к оси ж-ов, через — такое же напряжение по площадкам, перпендикулярным к оси у-ов и через ~— напряжение касательное, ур-ие упругой (срединной) поверхности м. б. написано в следующем виде:

Eh³ /3⁴w, „ _9⁴w. 3⁴w,

12(1 —σ²) 9ж⁴ ‘ “ dx²9y² *1" dy⁴ "*

+ Pi

3²w

dx³

+ P·.

d²w

dy²

+ 28

3²w дх dy

= 0.

(20)

Особое значение имеют вопросы устойчи-

ходящихся под действием сжимающих и касательных напряжений, для проверки стенок трубчатых колонн и стенок и ребер двутавровых и швеллерных балок, применяемых в клепаных колоннах.

П. с большим проги б ом. При исследовании П. с большим прогибом нельзя пренебрегать растягивающими напряжениями срединной плоскости.

Лит.: Б у С н о в И. Г., Строительная механика корабля, стр. 395—640, СПБ, 1914; его ж е, Напряжения в обшивке судов, СПБ, 1914; Тимошенко С. П., Курс теории „упругости, ч. 1, стр. 243—316,

П., 1916; его же, Устойчивость сжатых пластинок, «Известия Киевского политехи, ин-та», Киев, 1907; его ш е, Об устойчивости упругих систем, 1910, стр. 149—182, Киев, 1910; КояловичБ. М., Об одном ур-ии с частными производными четвертого норядка, СПВ, 1902; Д и н н и к А. Н., Круглая пластинка на упругом основании, «Известия Киевского политехнич. ин-та», Киев, 1910, стр. 287—306; его ж е, Об устойчивости сжатой круглой пластинки, там же, 1911, стр. 53—63; его же, Устойчивость круглой и прямоугольной пластинки в упругой среде, там же, стр. 305—316; Пистрянов Д., Изгиб тонкой пластинки, там же, 1910, стр. 309—373; Чал ы-ш е в К., К вопросу о расчете пластинок, лежащих на упругом контуре, «Сборник Ин-та инженеров путей сообщения», СПБ, 1914, вып. 87; Г а л е р к и н Б. Г., Стержни и пластинки, «ВИ», 1915, стр. 384—385; его же, Прямоугольные пластинки, опертые по краям, «Изв. Петроградского политехи, ип-та», П., 1915, т. 24, стр. 219—282; его ж е, К расчету тонких свободно опертых плит, «ВИ», 1917, 2; е г о же, Изгиб прямоугольных пластинок и стенок, «Изв. Петроградского политехнич. ин-та», 1916, т. 26, стр. 124—254; 1918, т. 27, стр. 187—319; его же, Исследование треугольных пластинок, «Известия Российской академии наук», П., 1919, стр. 223—238; его же, Изгиб треугольных пластинок, «Известия Петроградского политехнич. ин-та», 1919, т. 28, стр. 1—51; его же, Равновесие упругих пластинок, ограниченных двумя дугами концентрич. кругов и двумя радиусами, «Известия Российской академии наук», П., 1919, стр. 415— 426; его же, Пластинки в виде кругового сектора, «Известия Ленинградск. политехнич. ин-та», Л., 1925, т. 29, стр. 271—334; 1927, т. 30, стр. 461—485; 1928, т. 31, стр. 229—246; его же, Деформации и напряжения в прямоугольных пластинках под действием сосредоточенных сил. Инженерные сооружения и строительная механика, сборник, Л., 1924, стр. 3—23; его же, Термин, напряжения в упругих пластинках, там же, стр. 131—148; его же, Упругая пластинка в виде равнобедренного прямоугольного тр-ка под действием силы, сосредоточенной в точке, «Сборник Ленинградского ин-та инж. путей сообщения», Л., 1927, вып. 94; его ж е, К теории неразрезных пластинок, «ВИ», 1927, стр. 238—244; СурвиллоВ., Изгиб двухпролетной неразрезной пластины, «Морской сборник», Л., 1926, 11; N а у i е г, «Bulletin de la Socidtd philomathique», 1823, p. 95; P о 1 s s ο η, Mimoires sur l’6quilibre et le mouvemcnt des corps 61astiques, «Mdmoires de 1’Acad. des sciences», P., 1829,

t. 8, p. 237; С 1 e b s c h A., Theorie d. Elastizitat fester Korper, Lpz., 1862; С I e b s c h A., Thdorie d’6Iasticit6 des corps solides, traduite par Ваггё de Saint-Venant et Flammant, P., 1883; К 1 r c h Ь о f G., Vorlesungen liber mathem. Physik— Mechanik, 4Aufl., Lpz., 1897; Kelvin a. T a i t P. G., Element of Natural Philosophy, 2 ed., Cambridge, 1912; F 6 p p 1 A., Vorlesungen liber technische Mechanik, B. 5, 4 Aufl., B.—Lpz., 1922; Love A. E., A Treatise on the Materials Theory of Elasticity, 2 ed., Cambridge, 1927; Rayleigh, The Theory of Sound, 3 ed., v. 1, L., 1929; FSpplA.u.L., Drang u. Zwang, B. 1—2, 2 Aufl., B.—Lpz., 1924—28; F δ p p 1 L., Neuere Fortschritte d. techn. Elastizitats-theorle, «Z. furangew. Mathematik und Mechanik», B., 1921; Hertz H., Gesammelte Werke, В. 1, p. 288, Lpz., 1895; L ё v у M., Sur l’6quilibre d’une plaque rectangulaire, «CR», 1899, t. 129, p. 535; Estanave, Contribution 4 l’6tude d’iquilibre 61ast. d’une plaque minee, P., 1900; R i t z W., Theorie d. Transversal-schwingungen einer quadratischen Platte mit freien Randern, «Ann. d. Phys.», Lpz., 1909, B. 28, p. 737; H e n с k у H., Ueber den Spannungszustand in recht-eckigen Platten, Mch., 1913; Hencky Η., «Z. f. Math.

u. Physik», B., 1915, B. 63, p. 311; 1921, В. 1, p. 81; N 4 d a i A., Die Formanderung u. die Spannungen von rechteckigen elastischen Platten, Forschungsarb. auf dem Gebiete des Ingenieurwesens, B., 1915, H. 170/171; «z. d. VDI», 1914; N 4 d a i A., Die elastischen Platten, B., 1925; Mesnager, «Ann. des ponts et chaus-s6es», P., 1916; H u b e r Μ. T., Teorya plyt, Lwow, 1922; WestergaardH. M., Moments a. Strasses m Slabs, «Ргос. of the Amer. Concrete Institute», 1921,

v. 17; W e s t e r g a a r d H. M„ «Ingenieren», Kj»-benhavn, 1923, v. 32, p. 513—524; B i e z e n о С. В. en Koch J. J., «De Ingenieur», Delft, 1923, 2, p. 25; MarcusH., Die Theorie elastischer Gewebe u. ihre Anwendung auf die Berechnung biegsamer Platten, B., 1924; Ltwe, Pilzdecken, B., 1926; Schleicher F., Kreisplatten auf elastischer Unterlage, Berlin, 1926; Southwell R. V., On the Stability a. Shearing Forces of a Flat ElasticStrip, «Proc. of the First Intern. Congress for Appl. Meeh.», Delft, 1924, p. 266—274; К 4 r m 4 n Th., «Enzykl. d. mathematischen Wissen-schaften, B. 4, T. 2, H. 3, Lpz., 1910; G e c k e 1 e r J., Handbuch der Physik, hrsg. v. H. Geiger u. K. Scheel, B. 6, p. 210—231, B., 1928; G a 1 e r k j η B., Adapt

of Curvilinear Isoth. Coordinates to Integrate the Equat. of Elast. Plates, «The Messenger of Mathematics», L.—Cambridge, 1922, p. 99—109 («Изв. Росс, акад. наук», Л., 1924, стр. 55—66); Galerkin В., Berechnung d. freigelagerten elliptischen Platte auf Biegung, «Z. f. angew. Math. u. Mech.», Berlin, 1923, p. 113—117; G a 1 e r k i n B., Plaques minces limi-t6es par deux arcs de cercles concentriques et deux rayons sous Faction des forces concentres, «CR», P., 1924, t. 178, p. 919; G a 1 e r k i n B., ibid., 1924, t. 179, p. 1392; G a 1 e r k i n B., Equilibrium of Thin Rectangular Elast. Plates under the Action of Continuous a. Concentrated Loads, «The Messenger of Mathematics», L.—Cambridge, 1925, p. 26—39; Galerkin B., Contribution a la thiorie des plaques continues, «GC», 1928, t. 92, p. 181—184; Fliigge W., Die strenge Berechnung von Kreisplatten unter Einzella-sten, B., 1928. Б. Галеркии.