> Техника, страница 71 > Поверхность

Поверхность

Поверхность, протяженность двух измерений. Она м. б. рассматриваема как предел тела, у которого одно из измерений (толщина) неограниченно убывает, или как след линии (образующей), которая непрерывно перемещается в пространстве по определенному закону, причем может в процессе движения или сохранять или изменять свою форму. Если образующая—прямая линия, движение ее дает линейчатую поверхность (смотрите); частные виды линейчатых Π.: 1) конические (смотрите Коническая поверхность), все образующие которых проходят через одну общую точку; 2) цилиндрические, все образующие которых параллельны некоторой прямой (ось цилиндра); 3) коноидные (смотрите Коноид), образующая которых скользитпо двум непересекающим ся прямым. Если образующая П. плоская кривая, которая, не изменяя своей формы, вращается вокруг некоторой прямой (ось вращения), лежащей в ее плоскости,— получается т. и. П. вращения.

В аналитической геометрии (смотрите) П. определяется как геометрии, место точек, Декартовы координаты которых (ж, у, z) связаны одним ур-ием: F( ж, у, г)=0 if ли z=/(ж, у). Пример. 1) общее ур-ие цилиндрической П.: F(ж — аг, у — Ьг)=0, в частном случае, если ось цилиндра параллельна оси OY, ур-ие его: г=/(ж); 2) ур-ие П. вращения, полученной вращением образующей около оси OZ, имеет вид: z=/(ж²+у²); о параметрич. форме ур-ия П.см. Диференциалъная геометрия.

Ур-ие П. F(ж, у, z)=0 может быть алгебраическим или содеряшть символы трансцендентных операций; отсюда деление П. на алгебраические и трансцендентные.

Алгебраич. П. различают по их порядку и классу. Порядком П. называется степень п ее ур-ия, указывающая число точек (действительных или мнимых) пересечения П. с любою прямой. К л а с с П. определяется числом касательных плоскостей (смотрите Диференциалъная геометрия) к данной П., проходящих через любую прямую, заданную вне ее. Для П. тг-го порядка класс-вообще говоря равен η (η — I)². Определяется П. п-го порядка

(п + 1) · (п + 2) · (п + З), η·(η² + 6η + 11)

1-2-3 ¹ - 6

условиями, например заданными точками ее. Произвольная плоскость пересекает П. порядка п по плоской кривой порядка п и класса п (η — 1). Две П. порядков и η₂ пересекаются по пространственной кривой порядка прг ₂. Линия пересечения двух полостей одной и той же П. служит для нее двойною линией, а линия их соприкосновения— ребром возврата. Любую точку Р (а, b, с) пространства, лежащую вне П. w-ro порядка, можно принять за вершину конуса касательных к ней; порядок этого конуса η·(η~ 1) совпадает с классом плоского сечения П.; класс его равен классу самой П., то есть п-(п—1)². Через кривую касания этого конуса с П. F(x, у, z)=0 проходит так же и П., ур-ие к-рой:

to (*-«)+ щ(У~ Ь)+ (*-с)=0;

ее называют полярноюП. точки Р (полюс) относительно данной П. О кривизне и других диференциальных свойствах П. см. Диференциальная геометрия.

П. 1-го порядка или плоскость, простейшая из алгебраич. П., образуется движением прямой, проходящей · через неподвижную точку и пересекающей неподвижную прямую. Плоскость делит пространство на 2 симметрично расположенные части, может неограниченно перемещаться вдоль себя самой и налагаться на самое себя без складок и разрывов. Всякая прямая, имеющая с ней 2 общие точки, целиком принадлежит плоскости. Общее уравнение плоскости Ах + By+Cz+D=0 (1)

1-й степени и им;еет 4 коэф-та, то есть 3 независимых параметра (отношения ,коэф-тов); поэтому плоскость вполне определяется тремя условиями, наир, тремя заданными точками. Если в ур-ии (1) свободный член D=0, плоскость проходит через начало координат. Если А или В или С=0, она параллельна соответственно оси OX, OY или OZ. Если Α—Ώ=0 или B=D=0 или C=D=0, плоскость проходит через соответствующую ось. Если В=С=0 или С=А=0 или А= В=0, плоскость соответственно перпендикулярна к оси OX, 0Y или OZ. Если наконец А=В== С=0, а Т> =£ 0, то ур-ие плоскости сводится к невозможному равенству 1=0, к-рое однако можно рассматривать как ур-ие бесконечноудаленной плоскости. Ур-ие плоскости в отрезках:

х, υ i h

где а

;=1,

. » и 1 - ^ь С=- ^D

4 ’ ⁰ B^,L С

(2)

_А, - - - _в, V - _с — отрезки, отсекаемые ей на осях координат. Угол ξ между двумя плоскостями А_хх + В_ху + C_xz + + 1>ι=0 и А„х + В₂у + C₂z +П₂=0 определяется ф-лой:

cos ξ =

А1А2 -Ь В i В2 4- С1С2

(3)

j/Af + Bf + C?. γΑΐ + Bl + CI из которой вытекает условие параллельности двух данных плоскостей:

М _ В_х Ci А 2 В 2 С 2

и условие их перпендикулярности:

А_ХА₂ + В_ХВ₂ + С_ХС₂=0.

В нормальном ур-ии плоскости х cos а + у cos β + z cosy — p=0 (6)

параметрами служат длина перпендикуляра р, опущенного из начала координат на плоскость, и направляющие косинусы этого перпендикуляра. Чтобы привести общее ур-ие плоскости (1) к нормальному виду,

(4)

(5)

его надо умножить на нормирующий множитель

_, (7)

^_ 1/.4.2 + В2 + С2 ⁴

причем знак N всегда противоположен знаку свободного члена D ур-ия (1); тогда. в р=+ -

У А*

COS α= + cos β=± cosy=+

•г В 2-А

С 2

V М2

НВ2+С2

в

V Л2 + В2 ₊ са’

с

(8)

У А2 + № + са ’,

причем cos²<x + cos² β + cos²y=1. Расстояние d любой точки (а?!, у_х, г,) от плоскости, данной уравнением (1) или (6), определяется так:

d =

Ах i + Ву_х 4· Czi А В

У А*~-

В2 + С2.

= х_х cos а + у_х cos β + z_x cos γ - ρ; (9)

d отрицательно или положительно в зависимости от того, лежит ли начало координат и точка (х_х, у_х, z_x) по одну или же по разные стороны дайной плоскости. Расстояние между двумя параллельными плоскостями А_хх + В_ху + C_xz + D_x=0 и А_хх + В_ху +C_xz + + Р₂=0 равно:

^{/>г г}’^:! · (10)

J/Af + Bf+C?

Совокупность двух плоскостей F_x=0 и F₂=0 определяет линию их пересечения, то есть прямую. Ур-ие

F_x + kF₂=0 (И)

при постоянном к есть ур-ие некоторой плоскости, проходящей через эту прямую; если же к — переменный параметр, ур-ие (11) представляет пучок плоскостей, то есть совокупность всех плоскостей, проходящих через эту прямую (ось пучка). Три плоскости F_x=0, F₂=0 и F₃=0 пересекаются вообще говоря в одной точке. Ур-ие

F_x + kF₂ + lF_a=0 (12)

при постоянных к и Ϊ есть ур-ие плоскости, проходящей через эту точку; если к и I— переменные параметры, это уравнение дает связку плоскостей, т.е. всю совокупность их, проходящую через эту точку (центр связки).

П. 2-г о порядка. Связкою лучей и плоскостей называется вся совокупность, тех и других, проходящая через одну общую точку (центр или носитель). Две связки находятся в коррелятивном соответствии, если каждому лучу любой из них соответствует определенная плоскость другой, и обратно; если луч одной из этих связок перемещается в некоторой плоскости, соответствующая ему плоскость другой вращается около некоторой прямой. Вообразим две коррелятивные связки с различными носителями. Точки пересечения каждого луча любой из них с соответствующей плоскостью другой образуют одно и то же геометрии. место, называемое П. 2-го порядка.

Общие свойства. УравнениеП. 2-го. порядка

a_vx² + а_пу^г + й₃₃г² + 2 а₁₂ху + 2 a₂₃yz +

2a_nzx + Za_ux + 2а_иу + 2a_Mz + а_и - О

2-й степени относительно координат и содержит 10 коэф-тов, то есть 9 независимых параметров, почему эта П. определяется 9 условиями, например 9 заданными точками или 9 касательными плоскостями ее. П. 2-го порядка в то же время и 2-го класса, откуда следует: 1) со всякой прямой она пересекается в двух точках действительных или мнимых, лежащих на конечном расстоянии или в бесконечности, раздельных или слившихся; прямая, имеющая с П. 2-го порядка более двух общих точек, целиком принадлежит ей (прямолинейная образующая). 2) Через каждую прямую пространства проходит не более двух плоскостей, касательных к П. 2-го порядка. Произвольная плоскость пересекает ее по коническому сечению (смотрите), действительному или мнимому. Сечения параллельными плоскостями — подобные и подобно расположенные кривые 2-го порядка. Касательная плоскость пересекает П. 2-го порядка по коническому сечению, распавшемуся на пару действительных или мнимых прямых, пересекающихся в действительной точке (точка прикосновения касательной плоскости); если же кривая пересечения распадается на пару слившихся прямых, точка прикосновения становится неопределенной и касание происходит вдоль всей этой прямой (конус и цилиндр). В случае П. 2-го порядка для любой точки Р (а, b, с) пространства (полюс) полярная П. представляет плоскость, ур-ие к-рой:

«(«u* + Hi 2? + «13« л^- «и)г b((1₂]£ро>2₂у + u_2?>z-j-+ «24) + c(«3i® + а₃₂у + «зз« + α₃₄) +

+ (а_пх + a_i2y + a_l3z+a_u)=О и которая называется полярной относительно данной П. Для всякого луча, проходящего через полюс, точки встречи с П. гармонически сопряжены (смотрите Конические сечения) с полюсом и с точкой пересечения луча с полярною плоскостью. Если полюс перемещается по прямой, полярная плоскость его вращается около некоторой другой прямой; свойство это взаимно, почему прямые эти называются взаимными полярами. Если полюс перемещается в некоторой плоскости, полярная плоскость его вращается вокруг неподвижной точки, полюса первой плоскости. Если полюс лежит на самой П. 2-го порядка, полярная плоскость обращается в касательную. Если из 4 точек каждые 3 лежат в полярной плоскости 4-й, они являются вершинами так называемым полярного тетраэдра; каждая пара П. 2-го порядка имеет иек-рый общий полярный тетраэдр. Полюс бесконечно удаленной плоскости называется центром П. 2-го порядка; все ее хорды делятся в нем пополам; он удаляется в бесконечность, если П. касается бесконечно удаленной плоскости (параболоиды). Через центр проходят 3 главные плоскости, которые перпендикулярны к направлениям их бесконечно удаленных полюсов и которые пересекаются по 3 главным осям П. Главные плоскости являются плоскостями, а главные оси-осями симметрии П. 2-го порядка. Координаты центра определяются из системы ур-ий:

«11® + «12? + «13« + «14=0 )

«21® 4~ «22У + «23® "Г «24=0 .·

«31® "Г «32У 4“ «33« + «34 — О J

Классификация. Если поместим начало прямоугольной системы координат в центре П. 2-го порядка и совместим координатные плоскости с главными ее плоскостями, получим каноническое ур-ие П., содержащее только члены с квадратами координат и свободный член. Коэф-ты этого ур-ия выражаются через полуоси П. а, b и с. В зависимости от знаков коэф-тов и от обращения нек-рых из них в нуль, ур-ие это изображает различные типы центральных]!. 2-г о порядка.

1) Все 4 коэф-та одного знака:

ж², У², 22__

а² Ь2 > _С2 ¹

—мнимый эллипсоид. 2) Знак свободного члена противоположен знаку остальных:

ж² i a² i z²

₀2 т" μ т _С2 ¹

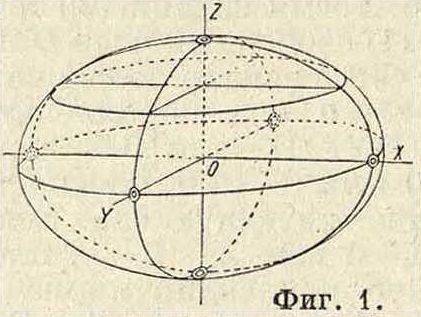
—действительный эллипсоид (фигура 1). Вся П. лежит на конечном расстоянии; всякая плоскость пересекает ее по эллипсу действительному или мнимому. 3) Знак свободного члена противоположен знаку лишь двух остальных:

^χ2 I у² _ ζ²

а² b² с²

= 1

—однополый гиперболоид (фигура 2). П. состоит из одной полости, неограниченно простирающейся в обе стороны; произвольная плоскость пересекает ее по действитель-

Фигура 2.

ному конич. сечению. 4) Знак свободного члена противоположен знаку лишь одного из остальных:

ж², и² _ ζ² _ _ ₁а² л" 6² с^{2 1}

—двуполый гиперболоид (фигура 3); он состоит из двух бесконечных полостей; произвольная плоскость пересекает П. по действительному или мнимому коническому сечению.

5) Свободный член равен нулю— конусы 2-го порядка: а) Все оставшиеся коэфициенты одного знака:

X²

а²

У²

b²

	__
	X 5
0
X	--->χχ
Фигура 3.

—мнимый конус. Единственная действительная точка поверхности—центр ее (0,0,0), лежащий в вершине конуса, б) Оставшиеся коэф-ты разных знаков:

^х I У² _ 2²

α² т 5² с^{2 :}

О

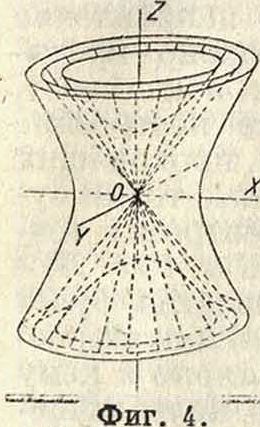
—действительный конус; он неограниченно простирается в обе стороны; всякая плоскость пересекает его по действительному конич. сечению. Если в уравнении конуса и в ур-иях однополого и двуполого гиперболой-

дов величины а, Ь и с одинаковы, ур-ие представляет асимптотический конус (фигура 4), образующие которого служат асимптотами плоских сечений, проходящих через общий центр обоих гиперболоидов. Однополый гиперболоид находится вне,а двуполый—внутри этого конуса. 6) Один из коэф-тов при квадратах координат равен нулю, свободный член не равен нулю—ц и л и н д р ы 2-г о п о р я д к а; они простираются в бесконечность, имеют целую линию центров (ось цилиндра), а) Все оставшиеся ко-эфициенты одного знака:

ж², у² а² Ь²

—мнимый цилиндр, б) Знак свободного члена обратен знаку двух остальных:

ж², у² 1

а² "г Ь²

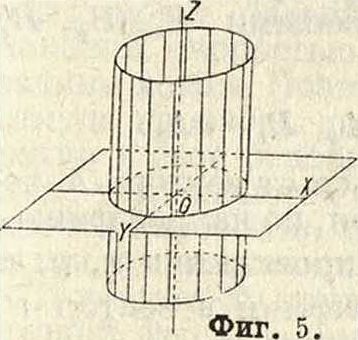
—эллиптический цилиндр (фигура 5); сечение произвольной плоскостью дает эллипс или пару параллельных прямых, в) Знак свободного члена обратен знаку одного из остальных:

ж² _ у» ₌ 1 о² 6» ¹

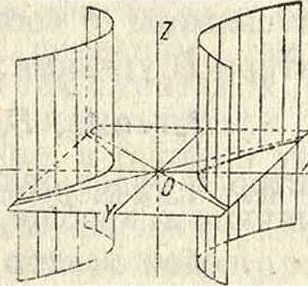
—гиперболич. цилиндр (фигура 6); плоское сечение^-гипербола или пара параллельных прямых. 7) Свободный член и один из

ФИГ. 6.

коэф-тов при квадратах координат—нули: пара пересекающихся плоскостей; причем а) знаки оставшихся коэф-тов одинаковы:

X² у² а² Ь*

о о

—пара мнимых плоскостей,пересекающихся по действительной прямой (линия центров);

б) знаки оставшихся коэф-тов различны: ж“ у“ а“ * Ь*

—пара действительных плоскостей, для которых линия пересечения служит линией центров. 8) Два из коэф-тов при координатах равны нулю, свободный член Ф 0: пара параллельных плоскостей; П. имеет целую плоскость центров, а) Оставшиеся коэф-ты одного знака:

^=-1 а²

—пара мнимых параллельных плоскостей, б) Оставшиеся коэф-ты разных знаков:

^жа=1

а²

—пара действительных параллельных плоскостей. 9) Три из коэф-тов ур-ия обраща

ются в нуль—пара сливающихся плоскостей. а) Свободный член равен нулю: пара действительного слияния плоскостей, б) Свободный член не равен нулю; ±1=0 рассматривается как ур-ие бесконечно удаленной плоскости (дважды взятой).

Остальные П. 2-го порядка имеют центр в бесконечности, почему их ур-ие нельзя свести к одному из рассмот-ренных видов, но они имеют 2 плоскости симметрии, и соответствующим выбором системы координат можно достигнуть того, чтобы уравнение их содержало только квадраты двух координат и первую степень третьей. _{Фиг> 7}_ Здесь возможны три случая: 10) Коэфициенты при квадратах координат одного знака:

ж². V² _ 2z а² b² с

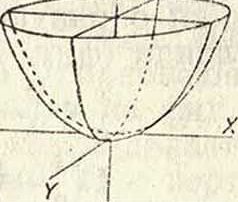
—эллиптич. параболоид (фигура 7); он состоит из одной полости,уходящей в бесконечность; сечение произвольной плоскостью—действительный или мнимый эллипс или парабола. 11) Коэф-ты при квадратах координат разных знаков:

Ж² у² _ 2Z а» Ь² ~ с

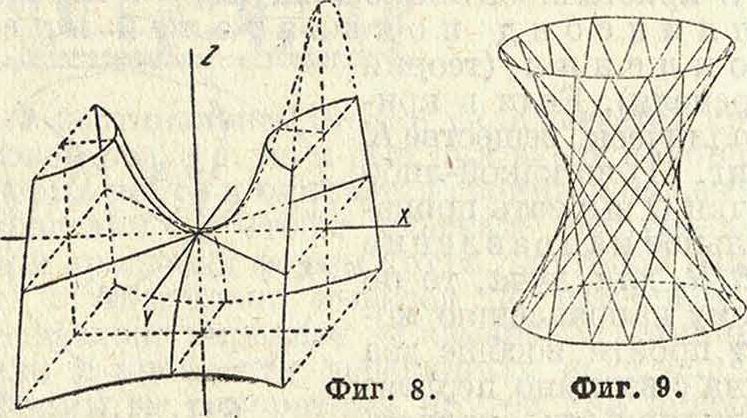
—гиперболич. параболоид (фигура 8). П. простирается в бесконечность, имеет седлообразную форму, плоское сечение—гипербола или парабола. 12) Один из коэфициен-тов при квадратах координат обращается в нуль:

ж² _ 2z

о^{2 —} с

—параболич. цилиндр, уходит в бесконечность, имеет бесконечно удаленную прямую центров; плоское сечение—парабола или пара параллельных прямых.

Прямолинейные образующие П. 2-го п о р я д к а. Из нераспадаю-щихся П. 2-го порядка принадлежат к числу линейчатых кроме конуса и цилиндра только однополый гиперболоид ж», V* _ ₌ i

а“ "* ь« с“

и гиперболич. параболоид ж² у² _ 2z о» ~ Ь² ~~ с ‘

Обе эти П.—частные случаи косых коноидов; обе имеют по 2 серии прямолинейных

образующих; каждая прямая одной серии пересекает все прямые другой и не пересекает ни одной прямой своей системы. Урав-

28

Т. Э. m. XVI.

нения образующих однополого гиперболоида (фигура 9):

“, у аЬ

;-Ч‘+9 1

I

•+Ι-Φ-!) I

‘(ί-ίΗ+ϊ )

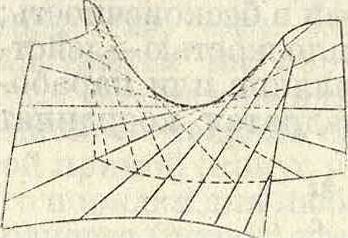
Ур-ия образующих гиперболического параболоида (фигура 10):

1-я серия;

2-я серия.

V

= к

X

‘6-9

“5-5-1

а b

i

е+9

21 с

1-я серия;

2-я серия.

Для этой П. все образующие 1-й серии параллельны плоскости

0;

все образующие 2-й параллельны плоскости а о

Фигура ίο. Характерным свойст вом настоящих линейчатых П. 2-го порядка является то обстоятельство, что сечение этих П. любою плоскостью всегда действительное.

Лит.: Власов А. К., Курс высшей матема-ики, т. 1, Аналитич. геометрия, диференциальное иинтегральн.исчисления,М.—Л., 1925; D arb oux G., Lecons sur la th6oric gdndrale Дея surfaces et Ies applications gSomdtriques du calcul infinitesimal, p. i—4, P., 1896—1914; DarbouiO., Principes de gdoindtrie analitique, P., 1917; Salmon G.—F i e d I e r W., Anal. Geometrie des Raumes, В. 1, S Aufl., B.—Lpz., 1922—23. См. Аналитическая геометрия, Диферен-циальная геометрия. В. Коновалова.

Поверхности второго порядка находят большое применение в различных областях знания и практики. В геодезии для графического изображения поверхности земли на основании съемок принимается за исходную поверхность эллипсоид, так называемый эллипсоид вращения Бесселя, у которого α= 6 377 397,1550 м, b=6 356 078,963 м, экс центриситет е²

а² - Ь²

_а2=0,0066743721 и сжатие (приплюснутость) р=^αγ=299,1528

В кристаллооптике большую роль играет эллипсоид показателей преломления (теория Френеля). Если в кри-сталлическ. веществе ET (фигура 11) из какой-либо точки О выбрать произвольное направление для луча, то по этому направлению могут пройти вообще два луча с взаимно перпендикулярными направлениями колебаний ОА показатели преломления

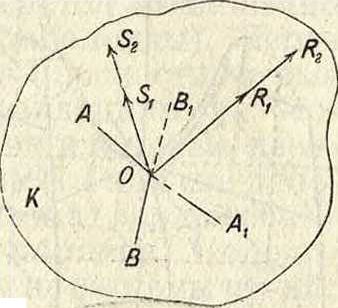
Фигура и.

i ОБ. Обозначая этих колебаний через щ и п₂, откладывают в обе стороны на направлениях колебаний ОА и ОБ отрезки, пропорциональные этим показателям преломления. Показатели преломления щ и и₂ вообще различны. Через ту яге точку О выбирают новое направление OSjSjs для луча и строят подобно предъ-идущему новые 4 точки. Опыт показывает, что если проделать такое же построение точек для всевозможных лучей, проходящих через точку О, то все построенные точки будут лежать на эллипсоиде с центром в точке О и с различными полуосями а, b, с. Любой радиус-вектор этого эллипсоида будет выражать показатель преломления луча,распространяющегося перпендикулярно к нему (точно или приблизительно) и колеблющегося в направлении радиуса-вектора. В частном случае этот эллипсоид может обратиться в эллипсоид вращения и в шар.

Остановимся еще на анизотропных телах-крист (кроме кристаллов правильной системы) и приведем другой пример эллипсоида—эллипсоид деформации (тензорный эллипсоид). Если кристалл подвергнуть даже равномерному нагреванию, то вследствие анизотропности расширение его по различным направлениям происходит различно. Три главных направления кристалла X, Y и Z будут главными о с я-м и расширения, взаимно перпендикулярными. Обозначим коэф-ты расширения на осях соответственно через а, b и с. Вектор А, проведенный изначала координат, после расширения превратится в вектор В, причем составляющие А_х, А_у, A_z вектора А будут связаны с составляющими В_х, В_у, В_гвектора В ур-иями:

В_х=аА_х, В у=Ь А_у1 В₃ — сА₃.

Вектор В будет отличаться от вектора А по величине и, вообще говоря, по направлению. Т. о. любой вектор г с проекциями х, у, г превратится после нагревания в вектор г с проекциями х, у, г, причем х=ах, у’=Ьу, z=cz.

Пусть до нагревания кристалла г=1; тогда концы всех таких радиусов-векторов будут лежать на шаровой поверхности ж² + у^г + z²=1.

После расширения кристалла эта поверхность обратится в

(?)^β + (ΐ)^β+(ί)·-ι.

то есть эллипсоид с полуосями a, b я с. Очевидно справедливо и обратное заключение: шар, образовавшийся после нагревания, был эллипсоидом до нагревания. Если скалярное произведение гг=xx + уу + zz

приравнять постоянной величине, наир. 1, и выразить х, у, z через ж, у, z и наоборот, то получим два эллипсоида деформации (тензорные эллипсоиды):

аж² + by² + cz²=1,

, ν}, г} _!

о "Г Ь ^ с

Правда, при некоторых значениях а, бис могут получиться и гиперболоиды. В теории пироэлектричества именно и рассматривается этот тензорный (центральный) тип пироэлектричества, обнаруживаемый равномерным изменением Р кристаллов (смотрите Спр. ТЭ, т. V, стр. 111). Такой же тензорный эллипсоид получается и в теории упругости— эллипсоид напряжений.

Гиперболоидальная поверхность находит применение например в машиностроении. Различают три рода зубчатых колес: цилиндрические, если оси валов параллельны, конич. зубчатые колеса, если оси пересекаются под некоторым углом, и наконец ги-перболоидальные зубчатые колеса (смотрите), если оси валов совсем не пересекаются. Гиперболоид осуществляется в конструкции инж. Шухова (Шаболовская радиостанция, Петровско-Разумовская водокачка).

При изготовлении зеркал для прожекторов и автомобилей (смотрите Параболическое зеркало) применяют параболоидальную поверхность. Параболические зеркала применяются и в астрономии для рефлекторов. Пара-болич. зеркала бывают стеклянные и металлические, у последних—поверхность параболоида вращения. д. Колянковский.