> Техника, страница 72 > Подпор воды

Подпор воды

Подпор воды, случай неравномерного движения потока жидкости вследствие его преграждения плотиной или запрудой, изменения уклона ложа, наличия препятствий на дне потока и сильного его сужения. Если точка А (фигура 1) есть начало и Н высота П. воды у плотины или превышение свободной поверхности воды в этом месте над нормальной глубиной воды h₀ при равномерном движении, то по мере подъема вверх по течению высота П. воды Z постепенно убывает до нуля, где П. воды кончается (точка В). Линия АВ подпертого уровня называется кривой П. воды. Горизонтальное расстояние L от начала до конца II. воды называется его гид-ростатич. длиной. Подпор воды, особенно для равнинных рек со слабыми уклонами, распространяется вверх по течению на далекое расстояние. Теоретически кривая П. воды асимптотически приближается к прямой

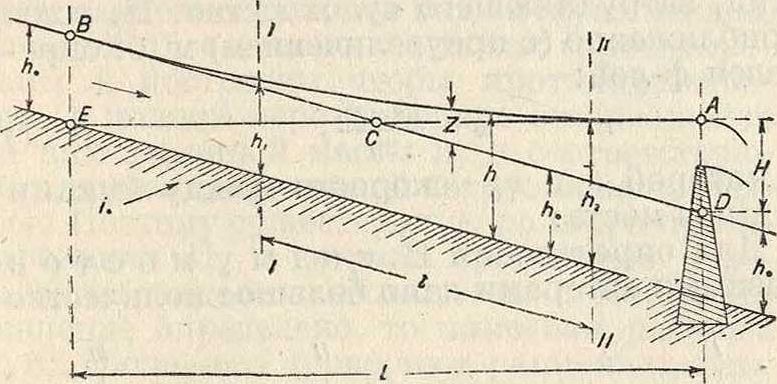
Фигура i.

равномерного течения воды BCD. Практически за длину П. воды принимают расстояние от его начала до сечения, в котором величина Z не превышает 3—5 см. В первом приближении, считая кривую подпора воды за параболу с вертикальной осью, имеющей вершину в точке А, получим длину П. воды равной L= ²Д, где г₀—уклон дна или бытового уровня при равномерном режиме. Приближенно, графически, длину П. воды можно определить, проведя горизонтальную прямую от точки А до пересечения с дном водотока в точке Е. Вследствие переменных величин живых сечений и скорости движение воды в подпертом русле будет неравномерным, поэтому для более точного определения длины и высоты П. воды исходят из ур-ия установившегося неравномерного движения:

(1)

dh,

(Э+

-у2

C2-.R’

где г—переменный уклон свободной поверхности воды, поднятой плотиной; а·—коэф. учета влияния неодинаковости скоростей на увеличение живой силы; г>, R и с—средняя скорость, гидравлич. радиус сечения и коэф. ф-лы Шези, д—ускорение силы тяжести.

Приведенное ур-ие дает возможность нахождения изменения глубины dh вдоль водотока для русла любой формы. Однако даже и при дальнейших его преобразованиях путем введения одной переменной h и выражения через последнюю других неизвест ных г, R и V интегрирование его затруднительно и возможно лишь постепенным приближением. Поэтому в практике ограничиваются лишь рассмотрением русла призматического, с неизменной формой вдоль водотока, когда ур-ие (1) приводится в частных случаях к квадратуре. Для случая широкого прямоугольного русла, с глубиной незначительной по сравнению с шириной потока, решение дано Прессом и уравнение для участка между двумя глубинами h_x и приводится к виду:

X¹=% - Vi - (1 - f) [ВЫ - ВЫ], (2) где j=У —; Β(η) есть ф-ия, полу ченная Прессом при интегрировании. Для того же случая Дюпюи, а затем Рюльман,

вводя отношение f и пренебрегая j, дают

^пО

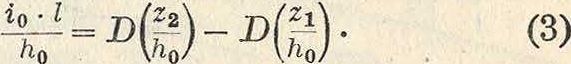
Голкмитт для параболич. русла, принимая j=0 и η=—·, получает ур-ие вида (3), в к-ром

D Jpj соответственно заменяется г(Х)· Значения ф-ий B(rj), D Ц) и Τ(η) даются в виде таблиц, приводимых в курсах гидравлики. Ур-ия 2 и 3 выведены, пренебрегая изменением коэф-та с с глубиной, и справедливы лишь только для тех видов призматич. русел, для которых они даны. Наличие к ним таблиц, значительно ускоряющих вычисления, приводит к их широкому распространению в практике и для русел, сильно отличающихся от приведенных частных форм. Из способов, пригодных для любых форм призматич. русел, получили распространение приемы Пахметева и Патикля. Прием Пахметева основан на указанной им эмпирич. зависимости:

ДНУ· ю выражающей, что квадраты модулей расходов данного русла относятся, как нек-рые степени ж соответствующих им глубин наполнения h и h₀. Величина х называется гидравлическим показателем руслаи имеет значение для разных форм русел от 2 до 6; к=со с ]/R есть модуль расхода и со—площадь живого сечения. Пользуясь зависимостью (4), интегрируя ур-ие (1), Бахметев получил его в конечном виде по форме, не отличающейся от ур-ия Пресса (2), но в к-ром ф-ия имеет другое значение. Для нек-рых значений ж составлены таблицы этих ф-ий. Применимость для любых русел неизменного сечения, наличие таблиц и учет изменения коэф. с с глубиной обусловливают важное значение и широкое применение приема Пахметева. Батикль,вводя линейный параметр ζ=γω*· R, зависящий от размера сечения, дает ур-ие кривой П. воды в виде:

^ia1 =f(^z-A-f(X, (5)

a-z₀ zq) z₀)

где α=ΊΐΧΐ, ζ₁₃ ζ₂ и ζ₀—значения параметров в сечениях I—I, II—II и при глубине V Способ Патикля дает возможность приближенно находить границу занесения наносами русла при П. воды, знание которой необходимо для определения полезных объёмов водохранилищ при решении многих задач водного хозяйства. Длина «твердого подпора» 1_п (фигура 2), на которую распространяется занесение русла, по Батиклю равна:

о · z₀F (0 + H

----j

(6)

где

a =

н-ftp. Z — Zq*

Z и Ы—параметр и глубина воды у плотины, ΙΓ—высота заиления перед плотиной. Ве

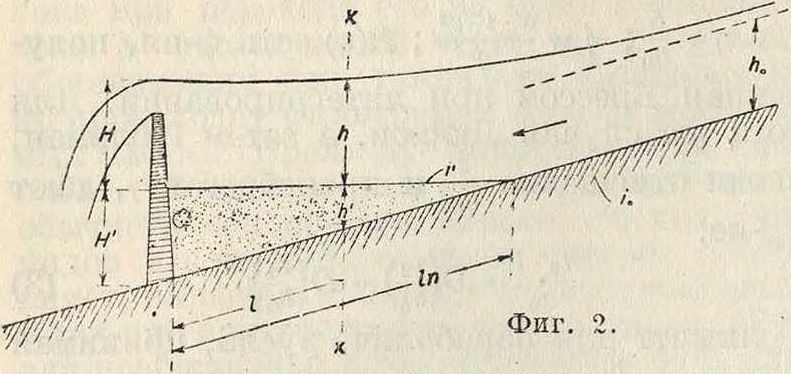
личина 1_п по (6), находимая последовательным приближением, дает возможность определить уклон г заиленного водохранилища и «твердый подпор» h в любом сечении х—х, а также построить кривую П. воды, значительно дальше распространяющуюся при заилении, чем в обычных условиях, что необходимо учитывать при определении затоплений. Достоинством приема Батикля является возможность построения кривых П. воды, пользуясь лишь одной таблицей или графиком для любой формы призматич. русла.

Значения?—

Zq·

с- ? ‘О		«+	F (*-) Zq’
1,000	— со	1,7	1,6691
1,001	-0,1366	1,8	1,7756
1,002	+0,0026	1,9	1,8805
1,003	0,0843	2,0	1,9842
1,004	0,1424	2,1	2,0870.
1,005	0,1876	2,2	2,1892
1,006	0,2247	2,3	2,2910
1,007	0,2561	2,4	2,3924
1,008	0,2834	2,5	2,4935
1,009	0,3076	2,6	2,6945
1,01	Q,3293	2,7	2,6653
1,02	0.4740	2,8	2.7959
1,03	0,5612	2,9	2,8965
1,04	0,6248	3,0	2,9969
1,05	0,6757	3,2	3,1976
1,06	0,7183	3,4	3,3981
1,07	0,7555	3,6	3,5985
1.08	0,7884	3,8	3,7988
1,09	0,8183	4,0	3,9990
1,10	0,8457	4,2	4,1992
1,12	0,8950	4,4	4,3993
1,14	0,9388	4,6	4,5994
1,16	0,9786	4,8	4,7995
1,18	1,0155	5,0	4,9996
1,20	1,0499	5,5	5,4997
1,25	1,1277	6,0	5,9998
1,30	1,1999	7,0	6,9999
1,35	1,2660	8,0	7,9999
1,40	1,3288	9,0	9.0000
1,50	1,4474	10,0	10,0000
1,60	1,5601	со	со

В естественных водотоках постоянно изменяется как форма русла, так и уклон дна. В этом случае для определения П. воды пользуются приемом последовательного суммирования, для чего разбивают реку на отдельные небольшие участки, для которых можно принять некоторые «средние» значе ния поперечных сечений и поверхностных уклонов воды. Задаваясь глубиною в конце участка, находят приведенными приемами глубину в начале и сравнивают ее с заданной в проекте, продолжая подбор до их совпадения. Последовательно переходя от участка к участку, строят кривуюП.воды на всем протяжений его распространения. Этим способом кривая П. воды м. б. определена с большей степенью точности, чем другими приемами. П. воды также возникает при протекании ее через мостовые отверстия, особенно при прохождении вешних и паводковых вод. Это явление аналогично случаю П. воды плотинами, и подсчеты ведутся тем же способом. Устройство в русле быков ABDC (фигура 3) вызывает П. уровня г₀е перед мостом (сечения I—I, II—II), спад е в пределах сооружения и подъем fd за мостом до· бытового уровня (сечение III—111). При этом различают истинный подпор eb=z, то есть подъем воды над бытовым уровнем i₀bcd_rнеобходимый для определения затопления вышележащей местности, и кажущий-с я подпор s (равный сумме высот истинного-П. воды—z, падения у моста β=1·ί₀ и понижения уровня c/=s₀), важный для определения перепада воды в мостовом отверстии, затрудняющего судоходство. П. воды приближенно (с преувеличением) м. б. определен ф-лой:

в которой V и v₀—скорости между быками и выше моста.

Для определения П.водыумостов разными авторами дано большое количество-

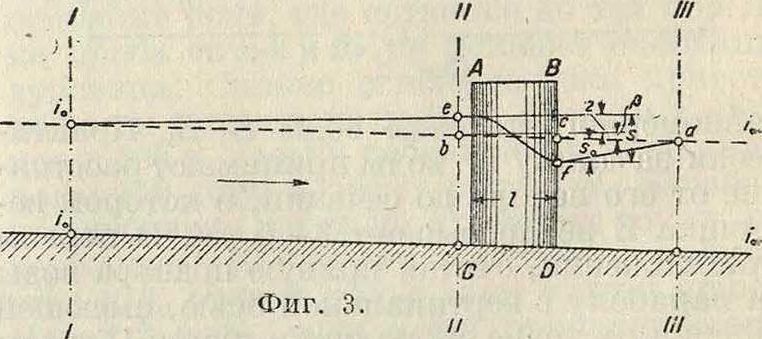
теоретич. ф-л, однако они не являются удовлетворительными и подсчеты по ним дают-между собою значительную разницу, доходящую до троекратной. Поэтому в настоящее время преимущественно пользуются эмпирическими формулами, из которых формула Ре-бока имеет наибольшее распространение и определяет истинный подпор z следующим выражением:

z=[<5„ - а (с5₀ - 1)] · [0,4а + а² + 9а⁴] ·

!>+£]·*.· <⁸> где <5„— коэф. формы, определенный Ребоком на основании опытов над моделями для быков разных форм; α= —коэф. стеснения русла (отношение части живого сечения, занятого быками, к живому сечению при бытовой глубине h₀); fc„=^т^|7ад^—СК0Р^0СТНЫЙ напор в бытовых условиях; В и Q—ширина и расход водотока у мостов. Для приближенного определения П. воды z Ребоге предлагает следующие ф-лы: при прямоугольных очертаниях быков г=2,1 а к_л (9)

при новых быках и плавном очертании их ζ=а · 7с₀. (ιΟ)

Ребоком дается ряд ф-л и графиков для П. воды в разных состояниях водотока при различных значениях <5₀. Помимо формул Ребо-ка получили некоторое распространение также формулы Крея.

Лит.: Д е и ш а А. В., Гидравлика для начинающих, стр. 73—76, М., 1924; БахметевБ. А., О неравномерном движении жидкости в открытом русле, Л., 4928; Таблицы для построения кривых подпора и спада в руслах с прямым уклоном по способу проф. Б. А. Бахметева, Л., 1929; Павловский Η. Н., О новых работах по гидравлике, стр. 2—10, Л., 1925; А х у т и н А., Новые методы построения кривых подпора в естественных руслах, «Гидротехнический сборник МВТУ», М., 1929, 2, стр. 107—118; Р а х м а-н о в А. Н., О построении кривых свободной поверхности для естественных водотоков при установившемся движении, «Известия Гос. научно-мел. ин-та», Л. 1930, вып. 20; Ф р а н ц и у с О., Гидротехнич. сооружения, пер. с нем., т. 1, стр. 97—99, М., 1929; В а-t i с 1 e, Nouvelle methode pour la ddtermination des courbes de remous, «GC», 1921, 23—24, p. 488, 515; Weyrauch R., Hydraulisches Rechnen, 5 Aufl. p. 216—240, Stg., 1921; Eehbock Th., Briickenstau und Walzenbildung, «Der Bauingenieur», Berlin, 1921, H. 13; R e h b о c k Th., Zur Frage des Briickenstaues, «Zentralblatt der Bauverwaltung», B., 1919, 37; К r e y H., Berechnung des Staues infolge von Querschnilts-einengungen, «Zentralblatt der Bauverwaltung», Berlin, 1921. С. Наплинский.