 > Техника, страница 72 > Подпорные стенки
> Техника, страница 72 > Подпорные стенки
Подпорные стенки
Подпорные стенки, стены, поддерживающие с боков земляные массы с естественным откосом или в виде искусственных насыпей. П. с. должны быть так спроектированы и построены, чтобы противодействовать в полной мере давлению опирающейся на них земляной массы и, в соответствующих случаях, временной нагрузки на последнюю. Поэтому существенную роль при проектировании П. с. играет правильное определение давления земли на нее. Когда это давление определено, то намечают размеры П. с., после чего проверяют рациональность намеченной формы ее. Наметку размеров стенки делают, пользуясь эмпирическими ф-лами, таблицами или практич. данными. Проверку производят графически—путем построения линии давления, следя за тем, чтобы последняя все время проходила в ядре сечения активной части стены и чтобы при этом не были превзойдены допускаемые напряжения каменной кладки стенки и допускаемые давления на грунт.
Определение давления земли н а П. с. При вычислении давления земли
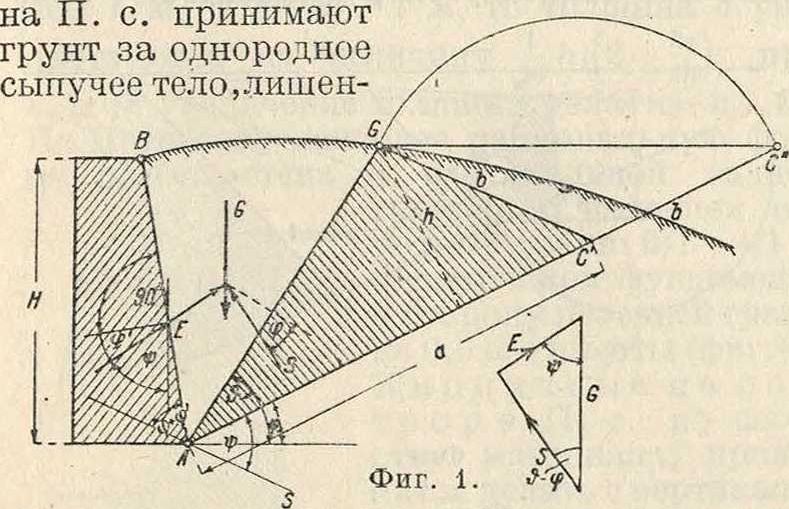
ное сцепления между его частицами, так что внутри земляной массы действуют лишь силы сжатия и трения. По предположению Кулона при малейшем движении (опрокидывании) П. с. в опирающейся на нее земляной массе образуется плоскость скольжения AG (фигура 1). Вес G земляной призмы ПВО должен находиться в равновесии с сопротивлением В
П. с. и с сопротивлением В плоскости скольжения, образующей с горизонталью угол #. Для характеристики условий трения в земляной массе служит угол φ. естественного откоса, отвечающий углу трения. Наименьшая величина сопротивления Е при устойчивом равновесии называется активным давлением земли. При этом предельном условии равновесия происходит скольжение земляной призмы вниз и сила от давления земли стремится опрокинуть или сдвинуть П. с. Наибольшая величина Е, потребная для равновесия, называется пассивным давлением земли; земляная призма ABG скользит вверх. Этот предельный случай равновесия наступает, когда П. с. нажимает на земляную призму, стремясь выпереть земляной клин вверх. В обоих случаях сила S образует с нормалью к плоскости скольжения угол трения φ.
Активное давление земли. По Ребхану плоскость скольжения AG делит пополам земляную призму, ограниченную плоскостью стенки АВ, плоскостью естественного откоса АС, поверхностью земли BG и плоскостью GC. Линия GC параллельна линии положения AS, образующей с линией естественного откосаугол Ψ, равный углу, образу-- емому давлением земли Е с вертикалью. Величина давления земли на единицу длины стенки определяется из ур-ия:
E=G~ — G-b (1)
АС а
Т. к. по Ребхану площадь AGC равна площади ABG и следовательно равна вели-
G
чине -, то у
G=y · площ. AGC 1=у а-- и Е=γ h-2~, (2)
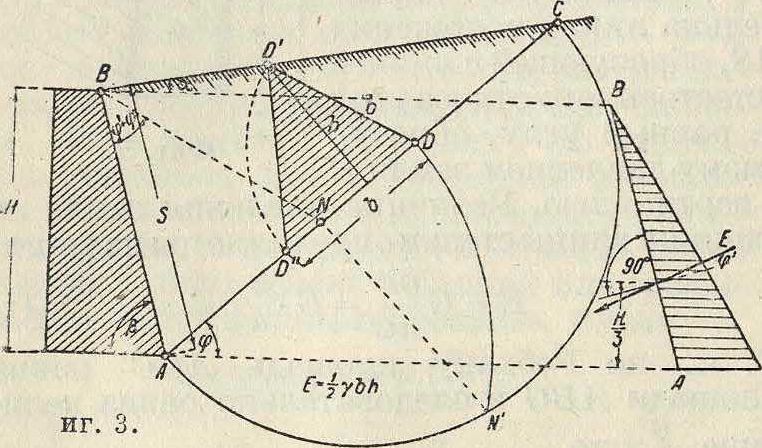
где γ—вес единицы объёма земли, a h—высота тр-ка AGC. Отсюда заключаем, что величина давления Е земли на П. с. длиной 1 метров определяется площадью тр-ка давления земли AGC. Действительное направление давления Е земли остается до сего времени невыясненным; вообще оно характеризуется величиной угла трения земли по стенке и выражается углом φ, образуемым силой Е с нормалью к поверхности стенки. При расчетах принимают, что величина угла φ может изменяться лишь в пределах от 0 до значений угла φ естественного откоса земли. В большинстве случаев берут φ·=φ если грунт влажный и пропитан водою, то берут φ=0. В последнем случае давление Е земли действует вертикально к поверхности стены. Распределение давления земли по поверхности АВ стены, в случае прямой ограждающей плоскости и прямой поверхности земляной массы, подчиняется тому же закону, что и при давлении воды (фигура 2). На практике поэтому принимают, что точка приложения равнодействующей Е лежит на одной трети высоты стены, считая от ее основания. Построение тр-ка давления земли при плоской ограждающей поверхности стены, прямом откосе и отсутствии временной нагрузки показано на фигуре 3. Сначала проводят через точку А под углом φ к горизонтали
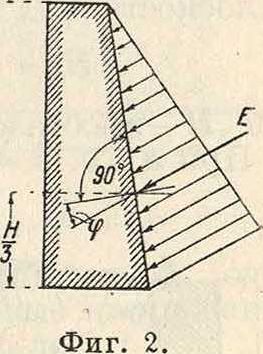
прямую АС, определяющую собой положение плоскости естественного откоса земли, и через точку В—прямую BN, параллельную основной линии или, что то же, образующую с прямой ВА угол φ+φ·, затем описывают на прямой АС, как на диаметре, полуокружность, проводят.ШУ±ИС, откладывают на прямой АС от точки А отрезок ΑΌ=AN, проводят DD || BN и откладывают DD"=DD. Заштрихованный треугольник DDD" и есть тр-к давления земли. Если земляной откос наклонен под углом а к горизонту, а плоскость АВ стены—под углом β, то горизонтальная составляющая Eh давления Е земли выразится ф-лой:
Eh
, ys
sin2 φ. + φ)
Γ1+ί/~,sin(y + <P’) ·sin (φ-α)Ε L Ί У Sin(/3+9J/j.sin(a + /3)J
(3)
•где s—длина следа АВ ограждающей плоскости при α= 0 (горизонтальный откос), jS=90° {задняя грань стены вертикальна) и <р=<р {плоскость АВ стены шероховата) или:
Eh — IУ IP г, ~г~~-2> (4)
•где II—высота стенки. При α= и, β=90° и <р
0 (плоскость АВ
стены гладкая, а грунт сырой) давление Е земли горизонтально и равно:
E=Eh=VIPt g»(45°-j)· (5)
В последнем случае давление земли на глубине Н на единицу площади будет равно:
9“ If=yStg* (45°(6) Если в формуле (5) принять φ=37° (среднее значение для насыпного грунта), то Έ= γΚ2, а для предельного значения γ =2,0, давле-ние земли Е=-. При α= φ (угол естественного откоса), φ — 0 и /?=90° получим:
Е=Еь~ Ут сое·?· (7)
Когда задняя грань П. с. наклонена в сторону земляной массы на угол δ, считая от вертикали, и α= 0 (горизонтальный откос), то давление земли выразится ур-ием:
1 уД2 _COS2 (б+φ)-__ (g
COS б (COS <5 + Sin φ)2
При тех же условиях, что в предыдущем случае, но при естественном откосе (α=φ) давление земли выразится величиной:
(9)
При наличии временной нагрузки р таковую заменяют эквивалентной нагрузкой, равной весу земли, высотой
К=У (10)
Соответствующее построение (фигура 4) дает новую (грузовую) линию ВС/, параллель ную откосу земли. На этой же фигура 4 приведено построение тр-ка давления земли при наличии указанной временной нагрузки р, причем так как линия естественного откоса
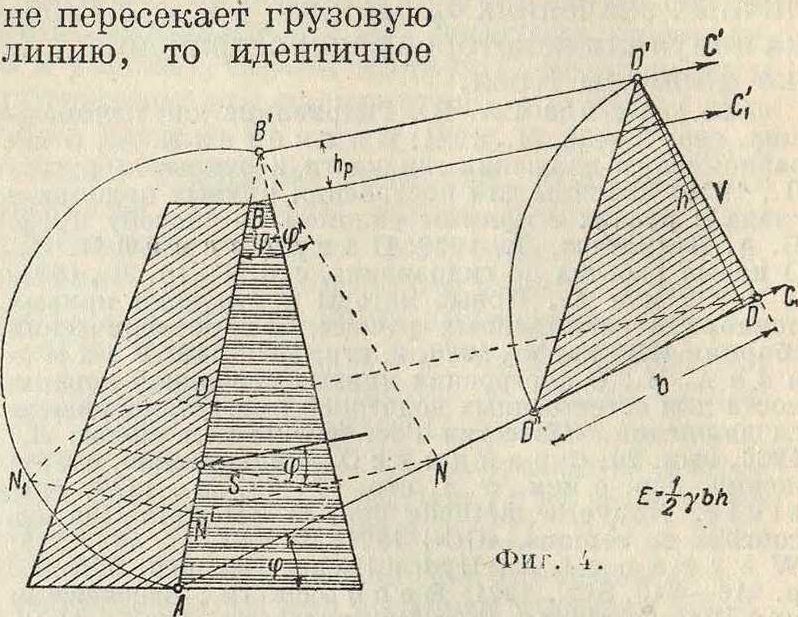
предыдущему примеру построение сделано не на линии естественного откоса, а на прямой АВ. Точка приложения силы Е лежит на одинаковой высоте с ц. т. трапеции давления земли. При горизонтальном откосе и вертикальной, совершенно гладкой задней грани стены давление земли и временной нагрузки м. б. определено по ф-ле:
E=I IP (γ +1) tg* (45° - I) · (И)
Здесь величина Е представляет собой сумму сил Еу (давление земли) и Ер (эквивалентное давление от временной нагрузки), причем принимают, что Еу приложена на одной трети высоты стены, считая от ее основания, а Ер—на половине высоты стены.
Пассивное давление земли. Определение пассивного давления земли (сопротивления земляной массы) производится по тому же методу, который был указан выше для активного давления земли, с теми лишь изменениями, которые связаны с переменой знаков у углов φ и φ на обратные. На фигуре 5 показано графическое определение пассивного давления земли для случая прямого откоса wg и прямой грани wa стены, причем для построения линии естественного откоса угол φ откладывают вниз
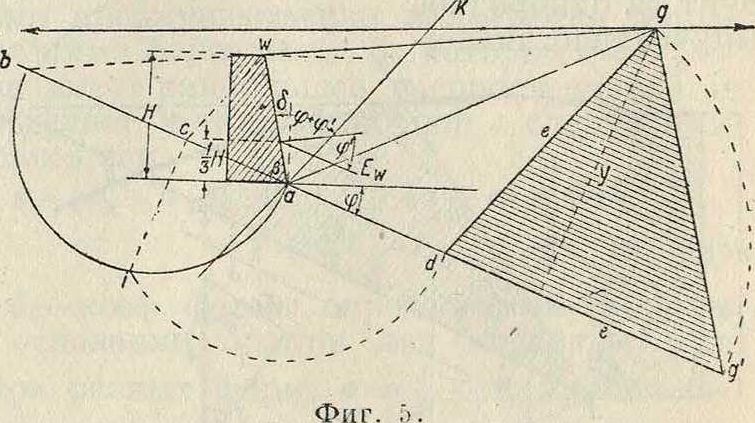
от горизонтали. Положение основной линии ак определяется углом φ+φ, откладываемым от wa в сторону призмы выпирания. Проводим прямую wc параллельно основной линии ак. Описанная на прямой ab, как на диаметре, полуокружность пересекается вертикалью oi в некоторой точке г. Определив эту точку, откладываем ad=ai и проводим agr||afe. Прямая ад—след плос-
кости выпирания, a dg=е—мерило сопротивления земли. Пассивное давление земли выразится при этом величиной:
(12)
где γ—вес единицы объёма земли, а у—· высота тр-ка dgg давления земли. При а==0 (горизонтальный откос), β=90° (δ=0; -задняя грань стенки вертикальна) и φ=0 сопротивление земляной массы будет равно:
Bw=|yHHg2(45° + |). (13)
.Если принять φ=37°, то Е1С=2γ II2, а принимая в последнем равенстве γ=2,0, получим Ew=4 Ы2.
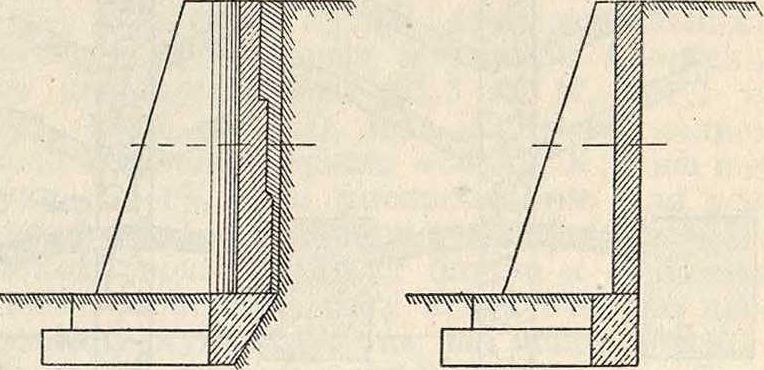
Определение размеров П. с. Для предварительного определения размеров П. с. можно пользоваться следующими ф-ламиипрактич.данными. Стены из сухой кладки. Передней грани придают заложение в 2/3 высоты; при стенках высотой свыше 10 метров наружную переднюю поверхность стенки делают ломаной, придавая верхнему скату (на высоте 10 м) заложение в 2/3 высоты, а нижнему—заложение в */5 высоты. Уклон передней грани с заложением в 7а высоты допускается лишь для •стен высотой не свыше 6 метров Заднюю грань стены делают вертикальной или с падением 6/1 в пределах насыпного грунта, а ниже его, в пределах естественного грунта,—параллельной передней грани стены. Толщина стены вверху м. б. определена предварительно по ф-ле:
+ (14>
где h—высота видимой части стены, fej—· высота насыпи поверх стены.
Стены, сложенные из бутового камня на растворе. Передней грани придают уклон с заложением в 75—Via высоты. Заднюю грань делают вертикальной. Для стены, имеющей переднюю грань с заложением в 7в высоты, а заднюю— вертикальной, толщина стены вверху м. б. предварительно определена из выражения:
d=0,44 + 0 2к, (15)
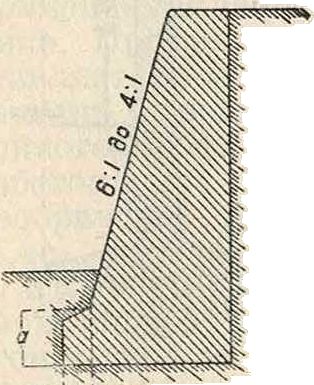
где h—высота стены. При этом высота насыпи поверх стены не должна быть более 1 метров Если hx > 1 м, то толщина d увеличивается на величину ^ ht{2 — при увеличение толщины делается в 0,1 h. По Петерсену наиболее рациональную форму^ имеет стена с вертикальной задней гранью, с падением передней грани 6/1—4/1 и с уширением фундамента в сторону передней грани на 0,6 его высоты (фигура 6). Кирпичные на растворе П. с., по свойству материала, приходится делать с вертикальными (передней и задней) гранями при горизон-_ „ тальных швах и с парад ен фигура 6. дельными наклонными гранями при наклонных швах. Чрезвычайно рациональной мерой в целях придания устойчивости и уменьшения веса стенки является замена части веса массивной П. с. трапецоидальной или прямо
угольной формы давлением действующей на стенку земляной массы. Получаются при этом П. с. тавровой или уголковой формы. Устойчивость такой стенки уже мало зависит от ее собственного веса, а давление земли на нижнюю полку угла само является той силой, которая препятствует опрокидыванию стенки. По конструкции такие стенки делают железобетонными.
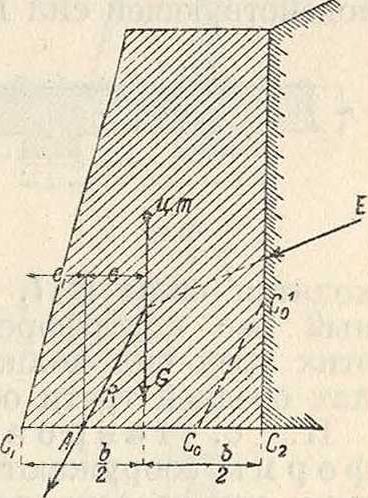
Проверка устойчивости массивных П. с. Для проверки устойчивости массивной П. с. определяют построением равнодействующую R (фигура 7) сил Е (давление земли) и О (вес каменной кладки). Равнодействующая эта должна пересекать основание стены в некоторой точке А, которая лежит в средней трети активной части стены (в ядре сечения), причем напряжения нигде не должны превосходить допускаемых. Если точка А лежит в средней трети шва СгС2 фиг, 7.
основания, то стена испытывает у этого основания лишь одно сжатие. Наибольшие краевые напряжения определятся при этом по ф-ле:
(16)
, JV, 6е где N—вертикальная составляющая равнодействующей R,F—площадь рассматриваемого шва, b—ширина шва (толщина стены у основания), е—эксцентриситет. Рассматривая участок стены длиною 1 м, можно формулу (16) преобразовать в следующую:
k=N
Ь ± 6е Ь‘
(16а)
Если точка А лежит вне ядра сечения, то давление передают на активную часть шва С1С0=Зе1 с тем, чтобы равнодействующая R проходила в средней трети части основания (7С0 (в ядре сечения). При этом наибольшее давление в крайней точке Схрассматриваемого шва найдется из ур-ия:
(17>
где <?].—расстояние точки А от ближайшего края шва, то есть точки Сг, а I—длина рассматриваемого участка стены. При I=1 метров формула (17) преобразуется в следующую:
С 301
(17а)
По ф-лам (16а) и (17а) обыкновенно и рассчитываются искомые напряжения. Часть стены на протяжении С0С2 основания, как изъятая из общей работы, м. б. подрезана параллельно наружной поверхности стены (С0Со0. При большой высоте П. с. требуется построение линии давления, с каковой целью профиль стены разбивают сечениями, параллельными основанию, на отдельные части, после чего находят для различных сечений центры давления, точки пересечения с равнодействующей соответственных веса и давления земли. Соединяя эти точки, получают линию д а в л е и и я, б. или м. близкую к кривой давления в стенке и дающую представление о характере распре-
деления давлений внутри стены. Для каждого шва определяют краевые напряжения, которые нигде не должны превосходить допускаемых.
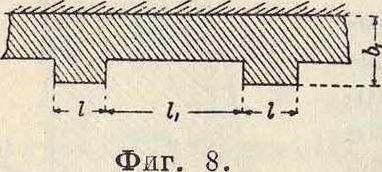
П. с. с контрфорсами. При усилении П. с. контрфорсами таковые располагают с внешней стороны стенки. Обыкновенно руководствуются следующими соотношениями размеров (фигура 8):
1=80b]/Г~ и 1-Ьц
(18)
где Ph—горизонтальная составляющая равнодействующей сил Е (давление земли) и G
(вес участка стены без контрфорсов). Ph должен быть воспринята контрфорсами. На участок стены с контрфорсом таким образом приходятся силы Е-1, Ph-lx и G (собственный вес контрфорса). Равнодействующая этих трех сил должна проходить в пределах средней трети основания стены.
П. с. тавровой и уголковой форы ы сооружают с ребрами и без таковых; они представляют собой наивыгодяей-шую форму сечения П. с. в смысле наименьших количеств потребныхматериаловивыем-ки грунта. Все части таких П. с. работают на изгиб. Часть АС фундаментной плиты (фигура 9), испытывающая давление грунта а снизу, рассчитывается как консольная балка. Другая часть СВ фун
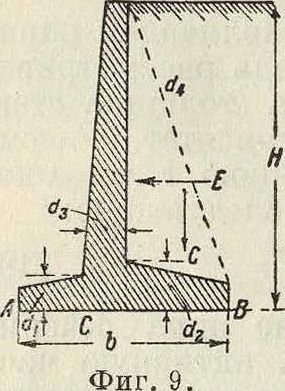
даментной плиты, на к-рую действует земляной груз сверху и давление грунта снизу, при наличии ребер рассчитывается как балка, частично зажатая на концах у ребер; при отсутствии ребер фундаментная плита СВ рассчитывается как консольная балка. Вертикальная или несколько наклонно расположенная стенка CD при наличии ребер рассматривается как салка на опорах, за каковые принимают ребра; при отсутствии последних стенка рассчитывается как консольная балка. Ребра рассчитываются как балки Т-образного сечения. Напряжения в частях П. с. и давление на грунт нигде не должны превосходить допустимых.
Жел.-бет. опорные стенки считаются более экономичными, чем таковые из трамбованного бетона, если 1 м3 железобетона обходится не дороже троекратной или четырехкратной стоимости 1 м3 трамбованного бетона. По Баумштарку безреберная форма стенки высотою до 4 it
более выгодна, чем таковая с ребрами. Расчет жел.-бет. П. с. производится по специальным ф-лам (смотрите ЛСелезобетонные конструкции). Характерным при этом расчете является то, что опрокидывающей силе давления земли противодействует вращающая в противоположную сторону сила веса массива грунта, лежащего над фундаментной плитой. Равенство обоих моментов обусловливает минимальные размеры плиты. Горизонтальное давление земли (5):
Ε~ γΗ* tg* (l5° - l)=* у IPs.
Если равнодействующая сил Е (давление земли) и G (вес П. с.) должна пройти через крайнюю переднюю точку ядра, то наибольшее давление на грунт будет:
(19)
При к=2,5 килограмм/см3 и среднем значении для у=1,6 т/м3 наибольшая допустимая высота П. с. получается равной ЕГжи:= 11,7 ж. Толщина частей П. с., изображенной на фигуре 9, без ребер м. б. определена по следующим ф-лам:
<h=Сх ]/Ж=С ХЯ У~ У Ее, (20)
к= Яу.
243
.-0,4 СХb VvE,
: сх ум,
- 0,407СХЕ ΐ/γΗε.
(21)
(22)
<*3
На высоте 0,63Я толщина стенки=-3· При наличии ребер надлежит dx вычислять по формуле (20), затем й2 по след, ф-ле:
с?2=Сх УЩ=0,2564* УуН, (23)
где х—расстояние между ребрами, толщина которых равна:
= ·0,25ίΟχχ У у Ее. (24)
Ребра отстоят друг от друга на 1,5—2,0 метров По Баумштарку наивыгоднейшее расстояние между ребрами равно:
1*
А. yi
где ψ—коэф., зависящий от допускаемых напряжений для бетона и железа, равный (в данном случае) 0.0039. При у=1 б00кг/м3
х=0,633/«!. О значениях коэф-та Сх в ф-лах (20)—(24) см. Железобетонные конструкции, формула (13). Мессер (Messart) рекомендует брать ширину а части АС фундаментной плиты равною:
α=
4 tg2 9>i-s2 tg2 (45°“ g)
H,
1(25)
8s tg <Pj
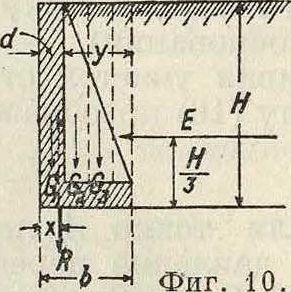
где s—коэф. прочности, φ—угол естественного откоса, ψχ—угол трения между стенкой и землей, II—высота стены в м. Для •определения размеров П. с. уголкового сечения (фигура 10) Вейске дает следующие ф-лы:
х
Sy-Sh + G2V (2 + d)
Gx + yG,
у =-Л + ΫΑ* + Β,
(28)
(27)
где
А =
0,75pd-Gi.
в =
0,75p-G2 ’ " G2(0,75p-G2) ’
л;—расстояние от равнодействующей до переднего ребра основания П. с.; р—допускаемое давление на грунт в т/м“·, d—толщина вертикальной стенки; (?!—вес стенки; G2— нагрузка на фундаментную плиту, приходящуюся на ширину, равную единице, включая собственный вес плиты и ребер; 8V—статич. момент передней стенки относительно переднего ребра основания П. с.; Sh — статический момент горизонтальной составляющей давления земли относительно того же ребра. Длины выражают в м, вес—в т. По Шеферу (Schafer) ширина фундаментной плиты в П. с. уголковой формы (фигура 10) без ребер определяется по следующим ф-лам при условии, что равнодействующая проходит через крайнюю переднюю точку ядра сечения и при отсутствии временной нагрузхси:
Фяг. 13.
&=Htg (450 — g )
ft - я tg (450-91/·^
(28)
Если растягивающие напряжения не допускаются, то
~~V (29>
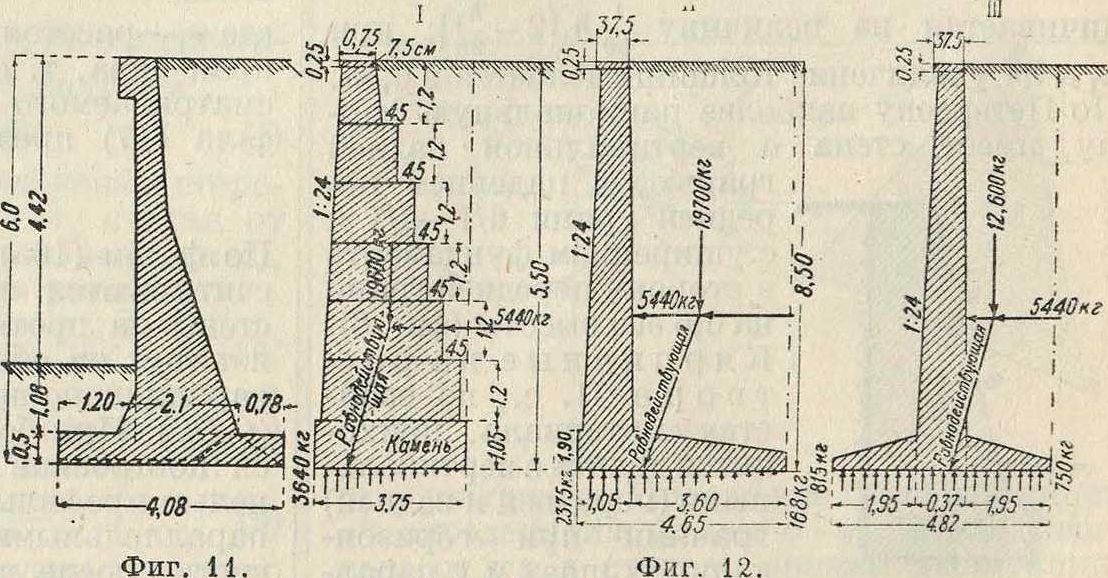
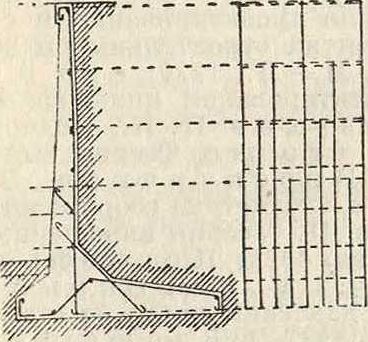
где к—допускаемое давление на грунт. В высоких П. с. устраивается для увеличения противовеса земли вторая горизонтальная плита на 1/2 высоты стенки. При наличии временной нагрузки таковая учитывается в виде эквивалентного веса земляной массы. На фигуре 11 представлен профиль П. с., применяемой часто в С. Америке. Профиль этот представляет собойпереходную ступень от массивного бетонного профиля к железобетонному. На фигуре 12 изображены три профиля П. с., из которых второй на 47,5%, а третий на 47,9% экономичнее первого при стоимости 1 м3 бетона 1-го профиля 34 герм, мар., 2-го и 3-го профиля 38,25 герм. мар. и 100 килограмм железа 28 герм, мар. На фигуре 13 представлена арматура П. с. таврового сечения.
П. с. в виде плоских вертикальных плит или сводов между контрфорсными опорами. Значи тельную экономию в материале против массивных стенок дает расчленение стенки на отдельные контрфорсные опоры,между к-рыми заделываются или плоские вертикальные бетонные своды (фигура 14) или плиты (фигура 15). Толщина последних определяется по давле-
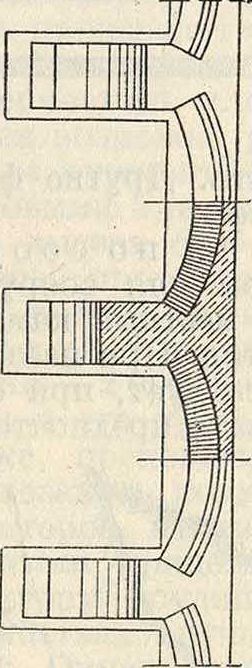
Фигура 14.
Фигура 15.
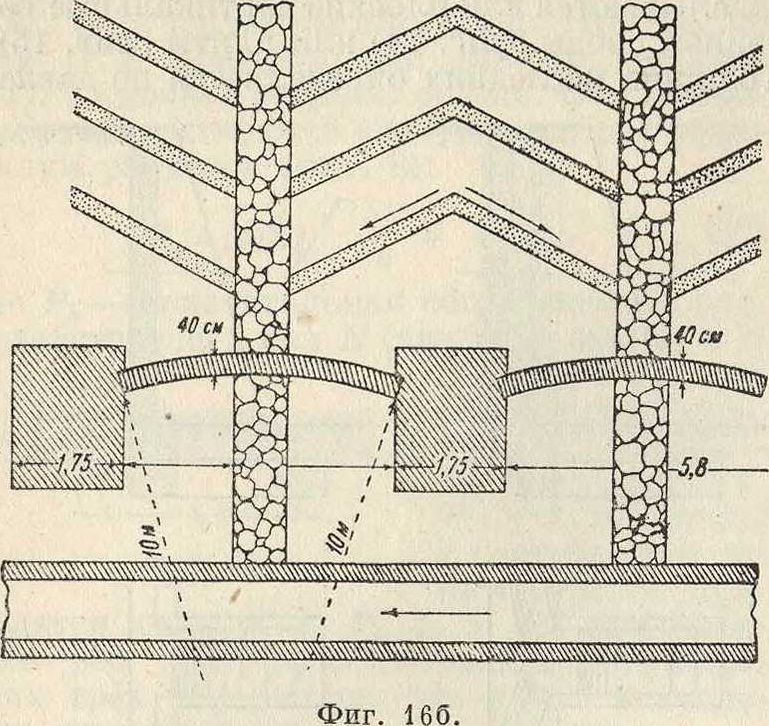
нию земли и величине пролета (расстоянию между контрфорсными опорами) и увеличивается книзу. Контрфорсные опоры, сооружаемые из бетона и железобетона (с вертикальной арматурой из круглого железа с хомутками), также утолщаются книзу, в виде плоских вертикальных жел.-бет. плит, поддерживаемых массивными бетонными контрфорсами. На фигуре 16а показан фасад и разрез, а на фигуре 166 план арочной П. с.
Глубина заложения фундамента П. с. Глубина заложения подошвы фун-
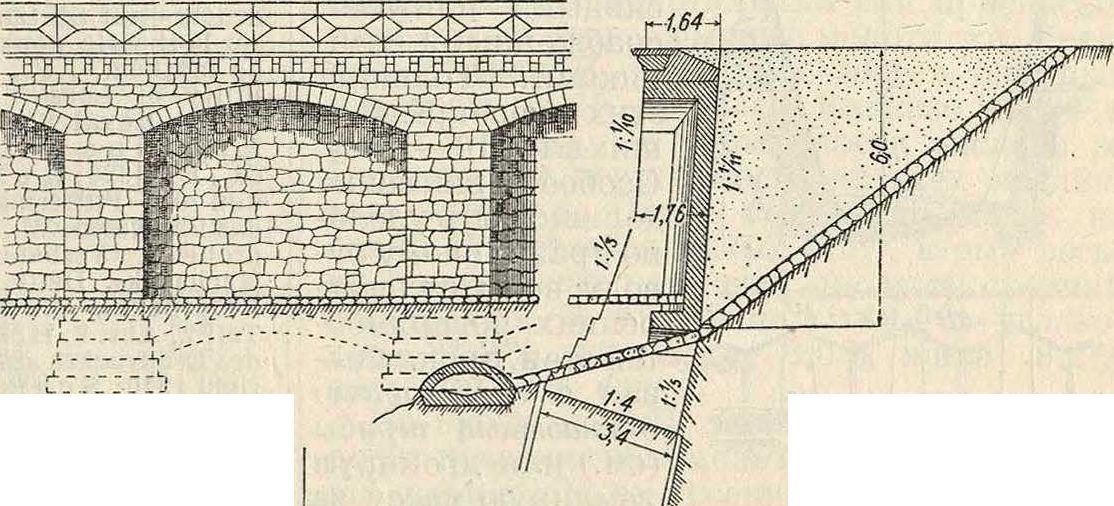
Фигура 18а. дамента П. с. определяется по формуле Паукера: h=mhy tg*(45°-|), (30)
в к-рой: h—глубина заложения подошвы фундамента, m—коэф. устойчивости, равный 1,75, к—допускаемое давление на грунт, γ—вес единицы объёма грунта, φ—угол
естественного откоса грунта. Другие ф-лы см. Фундаменты и основания.
Общие соображения по сооружению П. с. Материалом для сооружения П. с. может служить местный камень, кирпич, бетон и железобетон. При наличии камня различных пород следует, при одинаковой стоимости, отдавать предпочтение
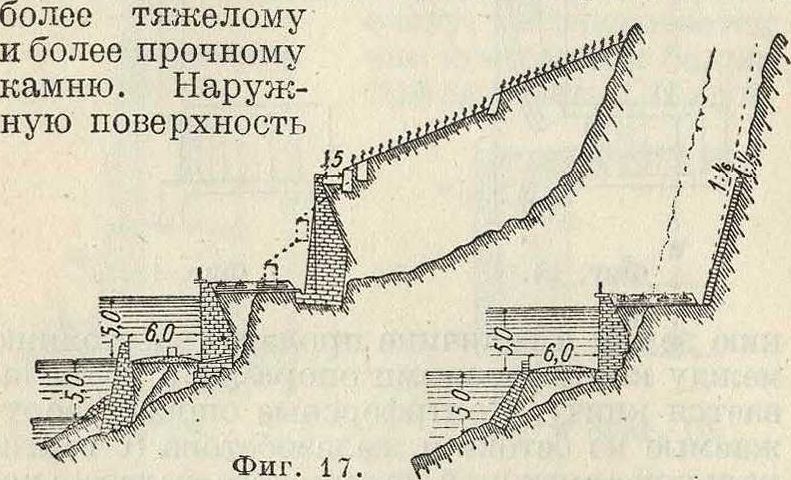
иногда облицовывают более плотным и прочным материалом (смотрите Облицовка). Наименьшей толщиной стенок считается: для бутовой кладки О,GO м, для кирпичной кладки— два кирпича. Все швы надлежит расшивать цементом. В массивных П. с. верх перекрывают массивными плитами, снабженными слезниками. Толщина этих перекрывающих плит 10—15 см. Особое внимание должно быть уделено правильному отводу воды от внутренних поверхностей стен, прокладывая с -этой целью дренаокные трубы (смотрите) или дренируя земляную массу за стенкой каким-либо иным путем (смотрите Дренаж) и устраивая водоотводные канавы на откосах (смотрите). Скопляющуюся в дренах или, при отсутствии таковых, за стенкой воду отводят наружу че рез особые проделанные для этого отверстия в нижней части стены (фигура 17) или выше, если имеются к тому подходящие условия (водонепроницаемый слой в нижней части стены, фигура 18). Земляную засыпку за стену производят слоями толщиной в 0,3 метров каждый, плотно утрамбовывая каждый слой. При этом следует избегать наклонных слоев, могущих образовать скользкие поверхности. При длинных П.с. надлежит принимать меры для парализования возникающих в стенках 1°-ных напряжений, влекущих за собой при нерациональной конструкции поперечные· трещины. Верхнюю часть стены следует сложить на цементном растворе, а позади стены на глубину 1 ми ширину 1 мнадлежит делать каменную пропускающую воду наброску, чтобы таким образом устранить возмояшость сдвига верхней части кладки (при морозах).
Лит.: Брилинг С. Р., Формулы и табли цы для расчета инж. конструкций, 3 изд., М.—Л. 1931; его же, Пособие для проектирования и составления смет и отчетности на строительные и дорожные работы, 3 издание, М.—Л., 1930; его же. Нормы для расчета и проектирования инженерных сооружений, М., 1927; Безухов Н. И., Подпорные стенки, М.—Л., 1930; его же, Теория сыпучих тел, М.—Л., 1931; Проскуряков Л. Строительная механика, ч. 2, Статистика сооружений, М.—Л., 1926; Велихов П., Теория инженерных сооружений, вып. 1, Москва, 1924; Прокофьев И. II., Теория сооружений, ч. 2, М., 1928; С к р ы льни к о в В., Определение давления земли на стены, «Гицротехнпч. сборн.», М., 1927, I; В aums t аг к, Die Konstruktion von Eisenbetonstiitzmauern, «В. u. E.», 1908; BouSRinesg, Sur les modes d’Oquilibre limite les plus simples, que peut presenter un massif sans cohOsion fortement comprlmd, «CR», 1874; Be-rrer, Standsicherheitsuntersuchung yon Eaimauern in weichem Lehmboden, «Bautechnik», Berlin, 1925; Conciitre, Note sur la poussOe des terres, «Annales des ponts et chaussbes», Paris. 1870; Cramer, Wider den sogenannten Kippsicherheitsgrad von Stiitz-mauern, «Bautechnik», Berlin, 1925; Engesser F., Neuere Versuclie iilier die Richtung u. Gr6sse des Erddrueks gegen Stiitzwande, «Deutsche Bauzeitung», Berlin. 1893; Franzius, Versuehe mit passivem Erddruck, «Bauingenieur», В., 1924, Η. 10; F r e u n d, Neue Untersuchungen zur Erddrucktheorie, «Ztschr. fur Bauwesen», B., 1921; KlrmSn Th., Elastische Grenzprobleme, «Verhandl. des Internat. Kongresses 1. technisehe Mechanik», Ziirich, 1926; К e p p 1 e r, Erddruck auf Parallelfliigel, «Bautechnik», B., 1925; Krey II., Erddruck, Erdwiderstand u. TragiShig-keit des Baugrundes, 3 AufI., B., 1927; Mohr O., Abhandlungen aus dem Gebiete d. techn. Mechanik,
3 Auli., B., 1928; Moht O., Theorie des Erddruckes auf Stiitzmauern, «Schweiz. Bauzeitung», Zurich, 1910; M 0 1 I e r, Ueber die Grosse des passlven Erddruckes, «Bauingenieur», 1924, H. 17; Morseh E., Die Berechnung von Winkelstiitzmauern, «B. u. E.», 1925; Μ U 1 1 e r-B r e s 1 a u H., Erddruck auf Stiitz-mauern, u. 1906; Peterman n, Neuere amerika-nlscbe I.i. iruckversuehe, «Ztrbl. d. Bauverwaltung», B., 1924· i· e t e r s e n R., Erddruck auf Stiitzmauern, B., 1924; Petersen R., Grenzzustande des Erddruckes auf Stiitzmauern, B., 1925; Ldvy M., Essai sur lathdorie nouvelle de ГёчиШЬге des terres, « tourn. de aiathtm.», P., 1873; R a n к i n e W., On the Stability of Loose Earth, «Philosophical Transactions of the Royal Society of London», L., 1857, v. 147; R a n к i n e W., Manual of Applied Mechanics, 20 ed., L., 1929; R e b h a η n G., Theorie des Erddruckes und die Futtermauern mit besonderer Riicksicht aul das Bauwesen, W., 1871; R e i s s n e r H., ZumErddruck-problem, «Verhandl. des Internat. Kongresses f. techn. Mechanik», Delft, 1924; Reissner H., Theorie des Erddruckes, «Enzx7klODadie d. mathem. Wiss.», B. 4, Tell 2, Abt. 2, H. 3, B*.—Lpz., 1910; Ritter, Theorie des Erddruckes auf Stiitzmauern, «Schw. Bauz.elt.», Zurich, 1910; Schmidtmann, Neuere Wege in d. An-wendung d. alten Erddrucklehrc, «Bauingenieur», В., 1924, Η. 15; Schultze, Erddruck auf Wmkelstiitz-mauern, «Ztrbl. d. Bauverw.», B., 1916; Streck, Bei-trag zur Frage des passivenErddruckes, «Bauingenieur», B„ 1926; Szlly, Beitrage zur coulombschen Lehre des Erddruckes, «Zeitschrifl d. Verb, deutscber Archi-tekten-u. ingenieurvereine», B., 1914, 37—42; P aas-well G., Retaining Walls, Their Design a. Construction, N. Y., 1920; Terzaghi K., Die Theorie d. hydrodynamischen Spannungserscheinungen u. ihr erd-bautechnisches Anwendungsgehiet, «Verhandl. des Inter -
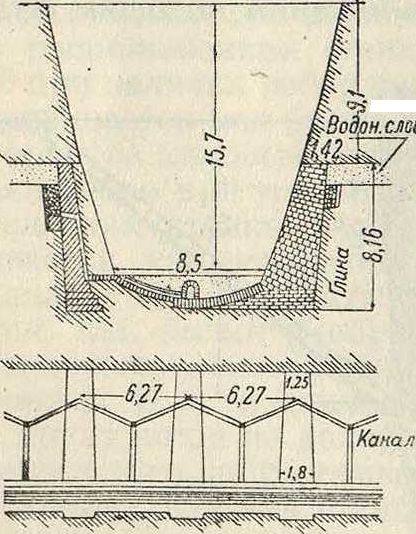
Фигура 18.
nat. Kongr. f. techn. Mechanik», Delft, 1924; Ter-zaghi K., Erdbaumechanik auf bodenphysikalischer Grundlage, Lpz., 1925; Weyrauch J., Erddrucktra-jektorien, «Ztschr. f. Arch.-u. Ingenieurwesen», Hannover, 1905; Willmann L., Stiitz-, Putter- u. Stau-mauern, Lehrbuch d.Tiefbaus.hrsg. v. K. Esselborn, B. 1, 8 AufI., Lpz., 1922; Winkler, Ueber Erddruck auf gebrochene und gekriimmte Wandflachen, «Ztrbl. d. Bauverwaltung», B., 1885; Prandtl L., Zur Harte plastlscher Korper, «Ztschr. filr angew. Mathem. und Mechanik», B., 1921; St. V e n a n t, «CR», 1870, 1884; Otzen R., Der Massivbau, Berlin, 1926; Wei sk e, Standfestigkeit d. Winkelstiitzmauern, «Zement u. Beton», B., 1907; Weiske, Beitrag zur Berechnung d. Stutzmauern, ibid., 1908. С. Брилинг.