> Техника, страница 72 > Полигонометрия

Полигонометрия

Полигонометрия, один из видов геодезии. съемки (смотрите), заключающийся в про-ложении угломерных ходов, или полигонов, с целью дать сеть опорных пунктов в развитие уже проложенной триангуляции (смотрите) или составить обособленную систему сомкнутых полигонов, которые служат основанием для дальнейших детальных съёмок. При проложении полигонометрич. ходов следует стремиться к тому, чтобы 1) ходы между пунктами триангуляции или между узловыми точками полигонометрической с е т и 1 класса были по возможности прямолинейны; 2) вершины углов хода на местности были закреплены надежными центрами (смотрите), наземными или подземными; 3) длины сторон хода были тщательно измерены обязательно два раза (туда и обратно) или в одну сторону, но двумя приборами, для чего мерные приборы должен быть хорошо эталонированы. При измерении углов обращается внимание на тщательную центрировку инструмента и целиков над вершинами углов полигона. Простейшим средством для этого является применение трех одинаковых штативов: для двух целиков или марок на задней и передней вершинах хода и для инструмента, установленного над вершиною измеряемого угла. Все 3 штатива тщательно центрируются, затем по окончании измерения угла инструмент ставится на место передней марки (без переноса штатива), задняя марка—на место инструмента, а передняя идет по ходу полигона и устанавливается с помощью освобожденного заднего штатива на следующей вершине хода. Метод измерения углов сообразуется соответственно с характером наличного инструмента (способом приемов или методов повторений). При увязывании полигонометрич. ходов принимаются во внимание узловые точки и распределяются веса сообразно длине и числу вершин отдельных ветвей этих ходов.

В зависимости от целей, которые предъявляются к П. в смысле точности конечных ее результатов, работы по проложению П. делятся на два главнейшие вида. 1) П. как опорная сеть для детальных съемок разного рода на больших пространствах применяется в практике общегосударственных работ, гл. обр. при изысканиях, землеустройстве; в этих случаях она базируется на пункты триангуляции 2-го и 3-го классов или же астрономические. 2) П. как обоснование для городских съемок в городах подобно предыдущему опирается на пункты триангуляции, прокладываемой специально для этой цели на всей городской территории. Самая П. делится на классы в зависимости от точности, которая от нее требуется. В городах с общей площадью всех земель > 10 км² ограничиваются самостоятельною сетью (сеть

1-го класса), на основе которой развивается полигонометрическая сеть 2-го класса, служащая основой для детальных съемок. При проложении полигонометрич. ходов между астрономии, пунктами последние не должны располагаться слишком густо, т. к. влияние уклонения-отвесных линий, различное по величине и направлению для соседних астрономии. пунктов, может исказить результаты П. Необходимо поэтому расположение астрономич. пунктов сообразовать так, чтобы ошибки в координатах их были немного меньше ошибок полигонометрических ходов. В практике государственных работ такого характера расстояние между астрономическ. пунктами принято в 50—60 км. II. как обоснование для съемок выполняется след, обр. Ходы прокладываются по ж. д., шоссе, «большакам» и просекам с таким расчетом, чтобы на каждом планшете съемки было не менее одного хода и, во всяком случае, чтобы расстояния между ними в наиболее удаленных частях оказались не более 20 км. Длина сторон хода не менее 300 метров Все поворотные точки отмечаются деревянными столбиками, высотою над поверхностью земли 0,5 метров Не реже чем через 5 км закладываются подземные центры (смотрите). При измерении линии вводятся поправки на наклон линии, для чего измеряются вертикальные углы. Горизонтальные углы измеряют 30-ск. теодолитом (смотрите), двумя приемами с перестановкой лимба (смотрите). Для увязки углов измеряются примычныеазилм/тм(смотрите) на тригонометрических пунктах и узловых точках, а также по линии ходов через 6—8 км. Центры городской П. закладываются на уличной мостовой или по тротуарам и должны служить и сохраняться на долгие сроки. На этом основании материалами для центров служат железо или чугун, камень или бетон: винтовые металлич. сваи, тянутые железные трубы, рельсы и прочие.

Непосредственное отыскание заложенных на мостовой центров весьма трудно; помимо того при переустройстве мостовых центры нередко замащивают. Поэтому каждый из них «привязывается промерами» к углам зданий на перекрестках улиц или к специальным чугунным маркам, которые закладываются в стенах зданий. Необходимо для каждого центра иметь не менее двух пересекающихся между собою промеров до марок или прочных и заметных предметов. Измерение сторон в городской II. производится различными мерными приборами, начиная от стальной точной «штриховой» ленты (смотрите Лента мерная) и кончая инварными проволоками, в зависимости от той точности, которой требуется достигнуть. Фиксация концов стальных лент совершается при помощи особых тяжелых башмаков, вбиваемых в землю или укладываемых на мостовой по направлению измеряемой линии. Далее или на шкалах ленты берутся отсчеты по постоянным индексам башмаков или, пользуясь постоянными штрихами ленты, на башмаках острием нарезают метки; для этой цели башмаки покрывают вверху гладкими свинцовыми пластинками. Второй метод— отметок постоянной длины ленты—предпочитается производителями работ. Лентою работают при постоянном натяжении динамометрами или грузами (5 килограмм). В последнем случае конструируются особые невысокие станки с блоками. Темп-pa записывается по термометру, заделанному в отрезок ленты и укладываемому на мостовой в тех же условиях, как и мерная лента, Наклон линий обычно измеряют по вертикальному кругу теодолитом, в исключительных случаях применяют нивелировку по башмакам. Для упрощения подсчета приведений заготовляются специальные таблички для разных углов наклонения по формуле ΔΪ=2 sin²1 или для различных разностей высот по ф-ле:

А 7 ь*

^Al-2l’

в этих ф-лах I—длина ленты, а—угол наклона линии к горизонту, h—разность высот двух соседних башмаков. При измерении линий инварными проволоками порядок производства работ обычный, соблюдаемый при измерении базисов, но в работе участвует не более двух проволок, и измерение производится только в одну сторону. Опыт показал однако, что при последнем способе работы одновременно с достижением точности измерения до 1 : 200 000 в II. могут вкрасться грубые ошибки. Штриховые стальные ленты дают точность измерения от 1 : 50 000 до 1 : 80 000. Однако систематические ошибки во втором случае м. б. значительными, что объясняется главным обр.трудностью учесть действительную ί° ленты при измерении. На этом основании рекомендуется применение деревянных 4-м жезлов, однако этот способ у нас сколько-нибудь широкого применения не имеет. В последнее время в практику П. для измерения расстояний начинают входить усовершенствованные дальномеры (смотрите) с горизонтальной рейкой (смотрите).

Измерение углов в городской П. производится б. ч. 30-ек. теодолитом, но в последнее время применяются и более совершенные инструменты, например теодолиты Цейсса с оптическим микрометром. Во всех случаях стараются создать комплект приборов из трех одинаковых штативов, теодолита и двух марок. Порядок работы таким комплектом приборов уже описан выше. В данном случае к ним добавляется еще оптический лот, аппарат, дающий возможность точно центрировать передний штатив над вершиною угла. Однако обходятся с более упрощенным оборудованием, которое сводится к двум добавочным штативам более легкого типа, чем при теодолите. Эти треноги устанавливаются над задним и передним центрами с помощью жестких ц е н т р и р о в, состоящих из тщательно оструганных деревянных круглых стержней, которые вверху под головкой штатива подвешиваются на цепочке т. о., чтобы нижнее острие стержня в точности держалось йад центром угла поворота П. Наведение трубою теодолита делается непосредственно на стержень. Такие центриры в настоящее время имеют большое распространение на производстве. Углы измеряются двумя приемами с перестановкою лимба. Для уравнивания хода, вытянутого между двумя опорными геодезич. или астрономии. пунктами, прежде всего переходят от географии, координат к сферич. прямоугольным Зольднера или Гаусс-Крюгера и вы числяют начальный и конечный примычный азимуты (дирекциональные угл ы). Но этим данным сперва подсчитывается невязка в углах полигонометрического хода. Если измерялись правые по ходу углы α_1; α₂, α₃, ., α_η, то азимут стороны i равен Ai=АЦ_г + 180° - а₍.

Если примычные азимуты обозначить через ММ и NN, число всех углов через и, то невязка в углах Δα равна

Δα=NN — I ММ + «180°— 2 ^α } №

В случае измерения левых по ходу углов при члене (»180°) должно поставить знак минус. Предел допускаемой невязки П. вычисляется по ф-ле:

Δα <

0 5t V 2 γη

Ϋτη

(2)

где t — точность отсчета по верньеру (смотрите), и—число углов, т—число приемов. Т. о. при -30-ек. теодолите и измерении углов двумя приемами невязка в углах выражается следующим неравенством Δα < 15" 3 |/п. Подсчитанная невязка распределяется поровну между всеми углами.

Если координаты опорных пунктов даны прямоугольные, а начальный и примычный азимуты измерены истинные, то должно ввести поправку д на сближение меридианов, которая вычисляется по ф-ле:

_{8 =} у_Ж1ум

R sini"

где Уц и у и—ординаты опорных точек первой М и второй N, R—средний радиус земного сфероида для средней широты пунктов М и N, к-рую можно взять с карты приближенно до 1°. Логарифм множителя lg для сфероида Бесселя приводится в нижеследующей таблице:

<Р	1- 1	<Р	,с 1	φ
	R sini"		е R sin 1”		‘B R sin 1"
40°	8,5109—10	50°	8,5101—10	60°	8,5194—10
42°	07	52°	100	62°	5 098
44°	06	54°	98	64°	92
46°	04	56°	97	66°	91
48°	08	58°	06	68°	91
50°	8,5101	60°	8,5194	70°	8,5088

После увязки углов делают вновь подсчет по вышеприведенной формуле (1), чтобы удостовериться в правильности цроизведенных вычислений; Δα должно теперь равняться нулю. Далее приступают к вычислению координат пунктов хода и подсчитывают невязки по оси абсцисс f_x и по оси ординат f_y, а затем поперечное смещение р конца хода по ф-ле:

₌ /»;ах] - щаю

. Γ;δ*.2 + [Лу]2

и невязка в направлении хода q по ф-ле:

п=ММ+ЫЩ.

Ε[Δχ’2+ [Дур

Величина р не должна превосходить Δα · sin 1 · L,

где Δα в минутах вычисляется по формуле (2), L—длина хода, [Δ*] и [Δί/]·—суммы приращений координат хода. Величина -|-не должна превышать относительной ошибки измерения линий тем прибором, к-рый уча-

ствовал в работе. Если невязки в координатах проложенного хода не выйдут из указанных пределов, то ход увязывается обычным порядком—распределением f_x и f_y пропорционально длинам стор.он полигона. Если полигонометрич. ходы, проложенные между тригонометрия. пунктами, пересекаются или, если сомкнутые полигоны имеют внутри перемычки в виде диагональных ходов, связывающих какие-либо пункты сомкнутого хода, то порядок увязки полигонов несколько меняется. В этих случаях точки пересечения ходов называются узловыми точками, и увязка, называемая у р а в н и в а-нием, производится следующим образом:

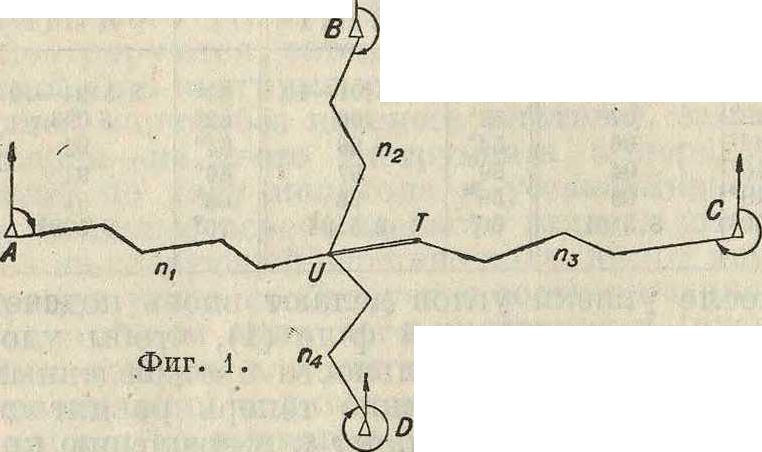
а) Два полигонометрич. хода, проложенные между пунктами триангуляции (фигура 1), пересекаются между собою в узловой точке U. Число сторон в ходах от пунктов А, В, С и Ώ соответственно равно п_1; п_г, п₃ и w₄. Прежде всего вычисляют азимуты сторон всех 4 ветвей ходов, начиная от пунктов триангуляции и пользуясь данными исходными азимутами и примычными углами. Вычисления ведут в направлении к узловой точке U и получают 4 значения для азимута произвольной стороны UT, примыкающей к углу

U. Этим азимутам а₁₍ а₂

а а₄ нужно при писать вес, обратный числу сторон полигона, то есть

Pi- ¹

Затем должно взять весовое среднее значение для азимута стороны UT, что будет равно

_α _ Pl^a 1 + Ρ2^α2 + Рз^д3 + Р4^α4 ₁^m~ · Ρΐ + Ρ2+ί>3+ϊ>4

Этот азимут считается окончательным и служит для вычисления невязок углов по ходам AU, BU,CU W.BU, как бы расположенным между двумя пунктами триангуляции (1-й случай). Невяз-j I ки распределяются поровну между углами ходов, и затем вычисляются окон

чательные азимуты сторон. В отношении вычисления координат ходов сохраняется тот же порядок. От пунктов триангуляции А, В, С, D, как исходных, пользуясь уже направленными азимутами, вычисляются координаты углового пункта U по всем 4 ходам. Координатам приписывается вес,·обратный периметру каждого хода, то есть

^{?1 =} ϊί^{; =} 9^а=ТГ₃’ 9i⁼

Среднее значение координат для узловой точки U вычисляется по весам: gi*i + д_гх₂ + д₃Хз + QiXj gi + g2 + йз Н- g₄ ’

v=^{Q,Vl + 9lV2 + ЯзУз + qiVi}.

^Um gi + 3a + «3 + Qi

Эти значения координат принимаются окончательными для точки U, после чего коорди наты всех 4 ходов увязываются между пунктами триангуляции и’угловою точкою обычным порядком. Точно так же поступают при наличии двух и более узловых точек, переходя последовательно от первой ко второй и т. д. и затем увязывая азимуты и координаты в обратном порядке, б) В случае сомкнутого хода, стянутого перемычками между узловыми точками U_lt t/₂, U_a и U4 (фигура 2), нельзя увязать сначала общий

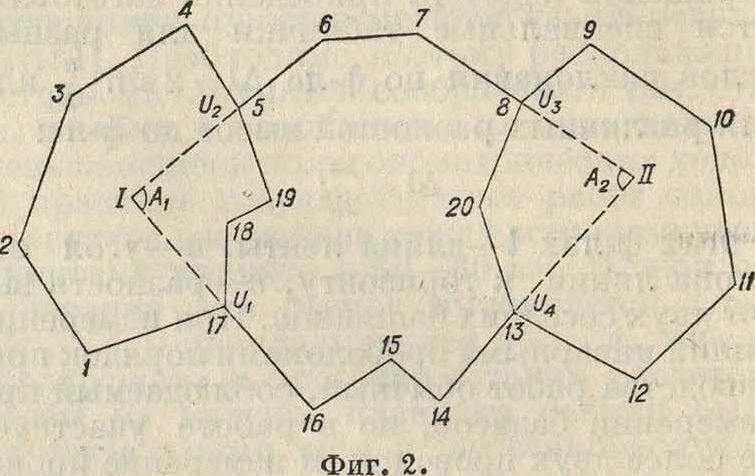
сомкнутый полигон, а затем вставить короткие ходы 17—5 и 13—8. При таком порядке увязывания весьма часто эти внутренние ходы получат поправки к углам и координатам настолько большие, что они будут изломаны, и окончательные углы и длины сторон будут отличаться от действительных на величины недопустимые. В виду этого проводится следующий порядок уравнивания. Из разности теоретич. суммы внутренних углов фигуры 17,1,2,3,1,5, I и суммы измеренных углов 17,1,2, 3, i и 5 находим величину угла M,. Точно также по теоретич. сумме внутренних углов фигуры 17, 18, 19, δ", I и сумме измеренных углов 5, 19, 18,17 находим второе значение для угла А[, причем при узловых точках в первом случае берут углы: при U₁ (180°—внешний угол 16, 17, 1), при Н₂ (180°—внешний угол 4, 5,

б); во втором случае берут: при TJ_r (180°— внутренний угол 16,17,18), при Н₂ (180°—внутренний угол 19, 5, 6). Значениям угла А и Αί приписывают веса, обратно пропорциональные числу сторон тех полигонов, из которых они подсчитаны, и затем берут их весовое среднее Д₄. Точно таким же путем находят весовое среднее для угла А_г. Получается новая сомкнутая фигура I, 5, 6, 7, 8, II, 13, U, 15, 16 и 17, в которой и подсчитывают невязку в углах. Эта невязка затем распределяется между углами, но также по весам, то есть всем измеренным углам этой фигура приписывается вес 1, а для углов А₁ и А₂—вес, который получен из предыдущих вычислений. Т. о. подсчитываются окончательные значения углов A_L и А_г. Затем их последовательно подставляют в суммы углов ранее намеченных фигур, распределяют невязки этих фигур на измеренные углы поровну, после чего вычисляют окончательные азимуты всех сторон данной системы полигонов. Далее вычисляются приращения координат и суммируются по тем же замкнутым фигурам, откуда находят приращения координат для ходов L IU₂ и П_гЛП₄ как весовые средние от каждой фигуры, причем веса берутся обратно пропорциональными периметрам полигонов. С этими данными подсчитывают приращения координат сом-

кнутой фигуры I, 5, 6, 7, 8, II, 13, 14,15, 16 и 17 и увязывают их обычным порядком, но приняв во внимание веса ходов TJ^ITJ^ и U₃I2i7₄. С полученными приращениями абсцисс и ординат этих ходов считаются как с окончательными и по ним увязывают приращения координат ранее взятых фигур. Далее вычисляют координаты всех точек системы полигонов. В описанном способе увязки системы сомкнутых полигонов вспомогательные ходы ДДЕ/а и и_з1Ш^ получаемые из вычислений, являются как бы эквивалентными фигурам левой и правой (фигура 2) и их заменяющими. Отсюда и весь способ увязки получил название метода эквивалентной замены. Необходимо отметить, что невязка в координатах сомкнутого полигона меняется в зависимости от перенесения начала координат из одной вершины в другую. Это объясняется тем, что при подсчете приращений выбрасывается угол при начальной точке. Так как ошибки углов различны, то и происходит такое различие в невязке всей фигуры.

Лит.: Чеботарев А. С., Способ наименьших квадратов, 2 изд., М„ 1928; Технич. инструкция по съемке и нивелировке городов, М., 1924; Инструкции по государственной топографич. мензульной съемке в масштабе 1 : 50 000, М., 1930. О. Дитц.