> Техника, страница 73 > Поляризация света

Поляризация света

Поляризация света, направленность его действий в плоскостях, поперечных лучу, проявляющаяся при нек-рых условиях; связана с · поперечностью световых волн. Последняя обнаруживается например в след, опыте. Если луч солнечного света проходит через рассеивающую среду, в которой взвешены частицы меньших размеров, чем длина световой водны, или через флуоресцирующую жидкость, то свет рассеивается (или излучается) неодинаково в различных направлениях несмотря на изотропность среды. Для любой плоскости, в которой лежит проходящий луч, получается следующая диаграмма интенсивностей света, рассеянного под разными углами (фигура 1): в направлении, перпендикулярном к проходящему лучу, кривая имеет углубление, и поперечная плоскость служит плоскостью симмет-

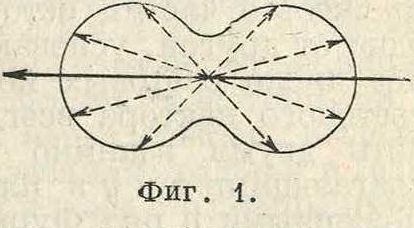
рии. В электромагнитной теории света поперечность световых волн (для изотропной среды) следует из условий:

div.E=0, div 11=0, (1)

где Е и Н— электрич. и магнитный векторы. Слагающие X, Y, Z электрич. вектора по осям координат для плоской монохроматич. волны м. б. написаны в виде

Х=А_х αο₅ω[ΐ-^±^±^), (2)

где т, п, р—направляющие косинусы нормали к плоскости волны, V—фазовая скорость волны. Диференцируя ур-ие (2) и подставляя в ур-ие (1), находим

А_хт + А_уп + А_гр=0. (3)

А_х, А_уг A_z пропорциональны косинусам углов, образуемых электрич. вектором с осями, и следовательно (3) выражает условие поперечности электрич. вектора и нормали к волне. Так же доказывается при помощи ур-ия (2) поперечность магнитного вектора к нормали. В опыте, описанном выше, обнаруживается только поперечность световых волн; в плоскостях, поперечных к лучу, излучение одинаково во все стороны и на диаграмме представится кругом (фигура 2,а).

а

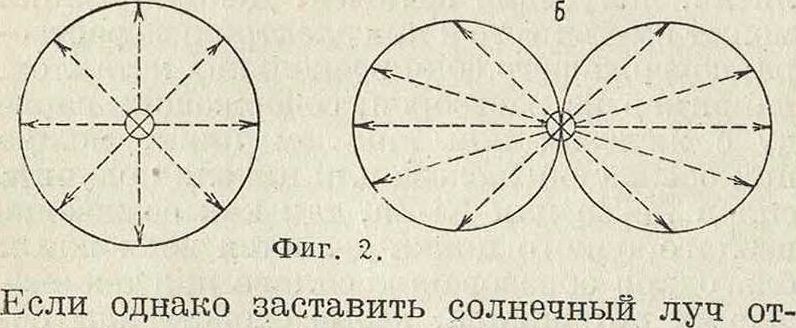
разиться под нек-рым подходящим углом от стеклянного зеркала и только после этого пропустить в рассеивающую среду, то излучение перестает быть изотропным и в плоскостях, поперечных к падающему луйу. Диаграмма излучения в поперечной плоскости представится в крайнем случае кривой, изображенной на фигуре 2, б: в некотором направлении свет совершенно не рассеивается, под прямым углом к этому направлению рассеяние имеет максимальное значение (смотрите Рассеяние света). Т. о. солнечный свет, отраженный от стекла, приобрел векторные свойства, стал поляризованным.

Виды П. с. Мгновенное состояние светового вектора не может наблюдаться; о П. с. мы судим по средним эффектам, получающимся за нек-рое время, в течение которого множество частиц источника, независимых одна от другой, успевают совершить огромное число световых колебаний. Состояние светового вектора всегда можно представить двумя взаимно перпендикулярными слагающими жиув плоскости волны, разложенными в ряд Фурье:

ж=2^· sin (ωί+ р) I

У =2В sin (ωί + q) J

В общем случае А и В, р и q независимы друг от друга и по определению (разложение в ряд Фурье) не зависят от времени t. Исключая ί из каждой пары монохроматич. компонент (4), получим для этой пары ур-ие эллипса:

%2 у 2 2Ху

αϊ + т - ab ^cos (Р - Я)=sin² (Р - q). (5)

Это значит, что для идеального монохроматического света вектор описывает своим концом (в общем случае) эллипс в плоскости волны с угловой частотой со. При р—д=0 или p—q — π эллипс вырождается в прямую

|т|=0. При р - q=± ~ и при условии

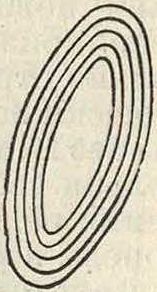
А=В эллипс принимает вид круга с вращением вектора вправо или влево (фигура 3). Соответственно этому различают 3 вида предельной П. с.: прямолинейную, к руг о вую и эллиптичес- ф_иг. з. к у ю (с вращением вправо и влево). Из уравнения (5) видно, что форма эллипса и его расположение не будут зависеть от со, если от последней не зависят разность фаз р — q и отношение амплитуд. В этом случае ур-ие

(4) представляет собою совокупность эллипсов различных размеров, но одинакового расположения и формы (фигура 4). При выполнении таких условий не-монохроматич. излучение м. б. также вполне поляризованным.

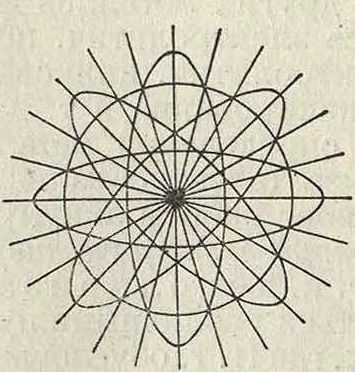
В большинстве естественных излучателей однако р — q и являются чрезвычайно сложными фигура 4. статистич. ф-иями со, резко меняющимися даже при ничтожных изменениях со, соответственно хаотич. беспорядку элементарных актов излучения. Конец суммарного электрич. вектора совершает в плоскости волны как бы броуновское движение, математически эквивалентное наложению всевозможных эллипсов, кругов и прямых (фигура 5). В предельном случае все направления в плоскости волны в среднем равноправны, век-торность практически исчезает, и луч обращается в неполяри-зованный, естественный. Между двумя крайними видами — вполне поляризованного и естественного— света располагаются лучи частично поляризованные, которые можно рассматривать как результат примеси того или иного вида поляризованного света к естественному. Следует различать свет частично линейно поляризованный, свет частично эллиптически поляризованный и свет частично поляризованный по кругу.

Для полной характеристики состояния поляризации светового пучка требуется знание 4 величин: интенсивностей естественного и подмешанного эллиптически поляризованного света, азимута осей эллипса и его эксцентриситета. Линейно поляризованный свет вполне определяется только указанием плоскости поляризации, то есть плоскости, перпендикулярной к световому (электрическому) вектору. Для характеристики луча, поляризованного по кругу, достаточно указать направление вращения.

.Для эллиптически поляризованного луча необходимо определить азимут осей, эксцентриситет и направление вращения. Все 4 признака полностью требуются для определения состояния поляризации частично поляризованного луча. Практически (причем иногда без достаточн. оснований) для характеристики частично поляризованного света ограничиваются обыкновенно измерением отношения интенсивностей компонент х и у, или дефекта поляризации,

где х—слабая, у—сильная компонента, откуда вычисляется степень поляризации

Ж²-у²

f Х*+у 2’

(?)

выражаемая в %. Разложение светового вектора на две взаимно перпендикулярных компоненты х и у автоматически осуществляется в явлении двойного лучепреломления (смотрите); математически к нему приходится прибегать при решении большинства поляризационных задач. В случае такого разложения естественного света компоненты х и у некогерентны, то есть не могут интерферировать (смотрите Интерференция света) при сведении в одну плоскость (опыт Араго-Френеля), что ясно из ф-лы (4), где фазы pvi q независимы друг от друга и хаотически меняются при изменении со. При наложении компонент возникнут всевозможные интерференционные усиления и ослабления, и общая интенсивность будет в среднем равна сумме слагаемых интенсивностей. В случае поляризованного света х и у когерентны, т. к. разности фаз p — q постоянны и не зависят от со; при сведении в одну плоскость компоненты интерферируют, и суперпозиция интенсивностей вообще нарушается. Для частично поляризованного света когерентность компонент ж и у также частична.

Закон Малю. Компоненты хну линейно поляризованного света, плоскость колебания которого образует угол а с осью X, равны соответственно A cos а и A sina и интенсивности ж²=А² cos² а, у²=A² sin² а (8)

(закон Малю). Для естественного луча угол а не может иметь определенного значения и

Ф-лы (8) и (8) служат основой различных применений поляризации для фотометрии. При двойном лучепреломлении в крист (8) и (8) не выполняются вполне точно вследствие неодинакового отражения компонент х и у на поверхности кристалла. Для исландского шпата при нормальном падении естественного света по Вильду

^=0,9725, для кварца весьма мало отличается от 1. В случае эллиптически поляризованного света мгновенные значения энергии компонент:

ж²=[A sin (ωί -j- р) sin a +

+ В sin (ωί + q) cos a]², ί/²=[A Sin (ωί + p) COS a +

+ В sin (ωί -f q) sin a]².

Средние значения энергии компонент в этом случае равны:

₂ а².,. в² „

ж²=₂ sm² a + - - cos² а у-=-у cos² а + — Sin² а

В самом общем случае частично поляризованного света средняя энергия компонент· выразится той же ф-лой (8") с измененными значениями амплитуд А я В. Ф-ла (8") является т. о. наиболее общим выражением закона Малю.

Возникновение П. с. Свет может поляризоваться 1) при излучении,

2) при распространении в веществе. Свет обычных (°-ных (нечерных) излучателей частично поляризован, например вольфрамовая проволока в направлении, перпендикулярном к оси, излучает свет, поляризованный на 20%, что согласуется с законом излучения Кирхгофа. Свет люми-несцирующих источников также во многих случаях частично поляризован. При возбуждении резонансного излучения и флуоресценции (смотрите Люминесценция) в парах, жидкостях и твердых телах вторичное излучение вообще поляризовано, причем степень поляризации может достигать 100%. (резонансное излучение ртути). Катодолюминес-ценция в газах при некоторых условиях также частично поляризована. В "сильных магнитных и электрич. полях при расщеплении спектральных линий (смотрите Магнето-оптика и Электрооптика) компоненты расщепления вполне поляризованы (линейно и по кругу). С другой стороны, естественный свет поляризуется частично или полностью при распространении в веществе, при диффракции, отражении,преломлении, двойном преломлении и рассеянии (смотрите Отражение света, Двойное лучепреломление и Рассеяние света). Поляризованный свет при распространении в веществе может менять характер поляризации, плоскость поляризации может повертываться (при отражении и в оптически активных телах), линейно поляризованный свет превращается в эллиптически поляризованный при полном внутреннем и металлич. отражении. Деполяризовать свет, превратить вполне поляризованный луч в квазиестественный возможно пропусканием его через мутную среду, например через молочное стекло. Относительно методов получения вполне поляризованного света см. Поляризационные приборы.

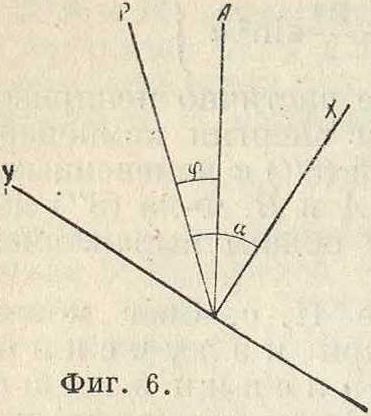
Хроматическая П. с. Если поляризованный свет проходит через двоякопре-ломляюшую кристаллич. пластинку и затем пропускается через прибор, выделяющий световые колебания только в одной плоскости (анализатор, например призма Николя—см. Поляризационные приборы), то наблюдаются различные интерференционные явления, имеющие большое применение при анализе П. с. (смотрите Полярископ). Кристаллич. пластинка разделяет колебания входящего пучка света на две слагающие: в плоскости главного сечения и в направлении. поперечном к этой плоскости (смотрите Двойное лучепреломление). Пусть X, Y (фигура 6) будут такие направления в пластинке. Параллельный пучок линейно поляризованного света с плоскостью колебаний, обра-

зующей угол а с X, отвесно падающий на пластинку, распадается в пластинке на две волны с амплитудами .A cos а и Asina. Анализатор пропускает только слагающие колебаний, образующие УГОЛ а - φ С×(фигура б), и компоненты двойного преломления выйдут через анализатор с амплитудами A COS a COS (а — φ) и A sin a sin (α—φ), соединенными в одну плоскость и способными интерферировать. Компоненты х и у распространяются в пластинке с разными скоростями соответственно различию показателей преломления п₁ и щ для обоих лучей разложения в кристалле. При прохождении через пластинку толщиною d лучи встретятся с разностью фаз

Δ=у (Цп_г - п₂). (9)

Т. о. интенсивность света, выходящего из анализатора, окажется равной

J=A² [cos² a COS² (a — φ) + sin² a sin² (a — 9?) + -j- 2 sin a COS a sin (a — φ) COS(a — φ) COS A] =

— A² [cos² φ — sin 2a sin 2 (a — φ) sin² ή J; (10)

она меняется в зависимости от углов аи<р, толщины пластинки d и длины волны А падающего света от 0 до А² (если пренебречь отражениями на поверхности кристалла). Если пластинка не плоско параллельна, но имеет форму клина, то поле зрения будет пересекаться чередующимися темными и светлыми интерференционными полосами (смотрите Компенсаторы). Если на пластинку падает сложный белый свет, то интенсивность J видимого света выразится интегралом •*2

J=j A^[cos²9>—sin 2a sin 2(a— φ) siiE-^J rfA, (11)

где и A₂—пределы видимого спектра. Вследствие зависимости Δ от А относительная интенсивность монохроматич. составляющих интеграла (11) будет иная, чем в падающем свете, и выходящий свет будет менять окраску при изменении углов a и φ и толщины пластинки. Это явление называется хроматической поляризацией, оно может произойти только в том случае, если падающий свет поляризован, то есть компоненты х и у когерентны, хотя бы частично.

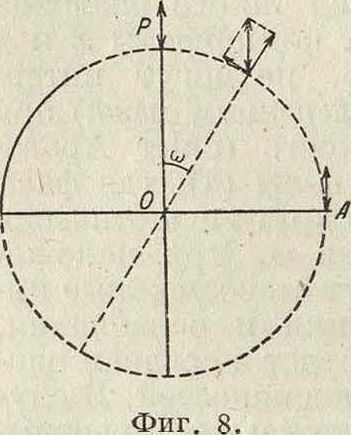
Явления интерференции становятся значительно сложнее в случае падения сходящегося пучка поляризованного света на кристаллич. пластинку, что достигается например в поляризационном микроскопе. Пусть АВ (фигура 7)—один из лучей кругового конусовидного пучка линейно поляризованного света, падающего на пластинку. Угол падения АВ равен г. При преломлении луч распадается на два луча, идущие под разными углами г_г и г₂ и поляризованные в двух взаимно перпендикуляры, плоскостях. Если выходящие пучки соединить линзой и пропустить через анализатор, то будет наблюдаться интерференция. Пусть оптическая ось кристалла совпадает по направлению с нормалью к пластинке и О—след оси конуса лучей на поверхности кристалла (фигура 8), ОР—направление колебаний в падающем луче, О А—направление колебаний, пропускаемых ана-лизатором. Если !

провести из О ок- jJ

ружность, то все _jog_

точки ее будут со- j I

ответствовать лу- ( д V

чам, падающим под ΙνΓ

одним и тем же уг-

лом К ОПТИЧ. ОСИ. фигура 7.

В плоскости изоб- ⁴

ражения все такие лучи, испытавшие двойное преломление, соберутся по кругу с одной и той же разностью хода. В данном случае интерференционная фигура состоит следовательно из чередующихся темных и светлых колец (вкл. л., 1—исландский шпат, вырезанный перпендикулярно к оптич. оси, в монохроматич. свете Na, между скрещенными николями). Картина осложняется однако поляризационными явлениями. Каждый луч разбивается вследствие двойного преломления на два: один с колебаниями в плоскости главного сечения (то есть в радиальном направлении—фигура 8), другой с колебаниями, перпендикулярными к: этой плоскости (то есть в тангенциальном направлении—фигура 8). Амплитуды этого разложения будут зависеть от азимута со. В направлении ОР есть только радиальная компонента, которая не будет пропускаться анализатором (пропускающим в разбираемом случае только колебания, перпендикулярные к ОР). В направлении ОА могла бы пройти также только радиальная компонента, но ее нет под этим азимутом в падающем свете. Т. о. по двум направлениям ОР и О А свет будет полностью· погашен, по середине между этими направлениями свет будет максимальным, на круговую интерференционную картину наложится темный крест; если направления колебаний падающего и пропускаемого анализатором света параллельны, то крест будет светлым. Интерференционные кольца являются кривыми равной разности хода, зависящей от А, поэтому при освещении белым светом кольца становятся радужными. Кривые равной разности хода называются изохроматами. Распределение интенсивности в темном или светлом кресте зависит только от азимута шине зависит от А (если только от А не зависит положение оптич. осей), поэтому при освещении белым светом крест не имеет окраски, он черный или·белый (интерференционные фигуры такого типа называются и з о г и р а-м и—линиями равного поворота). Для точек интерференционной картины, близких к центру, углы г_г и г₂ (фигура 7) мало отличаются друг от друга, и оптич. разность I хода обыкновенного и необыкновенного лу-

Τ. ΰ,

Silii

ΐ. о.

чей, выходящих из кристаллич. пластинки:

Д „ Д(П2-Щ)Л ~ λ cos г

Эта формула (с указанным приближением) справедлива для любой кристаллич. пластинки, вырезанной как угодно по отношению к оптич. осям; в ней (щ — щ) является ф-ией угла падения. Для случая двухосного кристалла· из общей теории двойного лучепреломления следует (с указанным приближением), что

Δ ⁼ ;,Гз Л^п° ~ ^п^>^sin ^ ^{sil1 φ}ζ· (¹²)

Здесь η₀ и п_е—г лавные показатели преломления обыкновенного и необыкновенного лучей, <р₁ и <р₂ — углы, образуемые средней нормалью к волне с оптич. осями кристалла. Удобную геометрия. интерпретацию формула (12) получает, если построить изохроматическую поверхность, или поверхность равной разности хода. Пусть вершина конуса падающих лучей сходится на передней поверхности кристалла. Будем откладывать от этой точки по разным направлениям отрезки, которые должен пройти луч в кристалле, чтобы приобрести определенную разность хода Δ. Поверхность, соединяющая концы таких отрезков—векторов, и будет поверхность равной разности хода. Обозначив

2nd

λ₀ cos г

(13)

имеем следующее ур-ие поверхности равной разности хода:

ρ sin φ_χ sin φ₂=Const. (14)

Для одноосного кристалла φ_χ=φ₂, и ур-ие принимает вид:

ρ sin² φ=Const. (15)

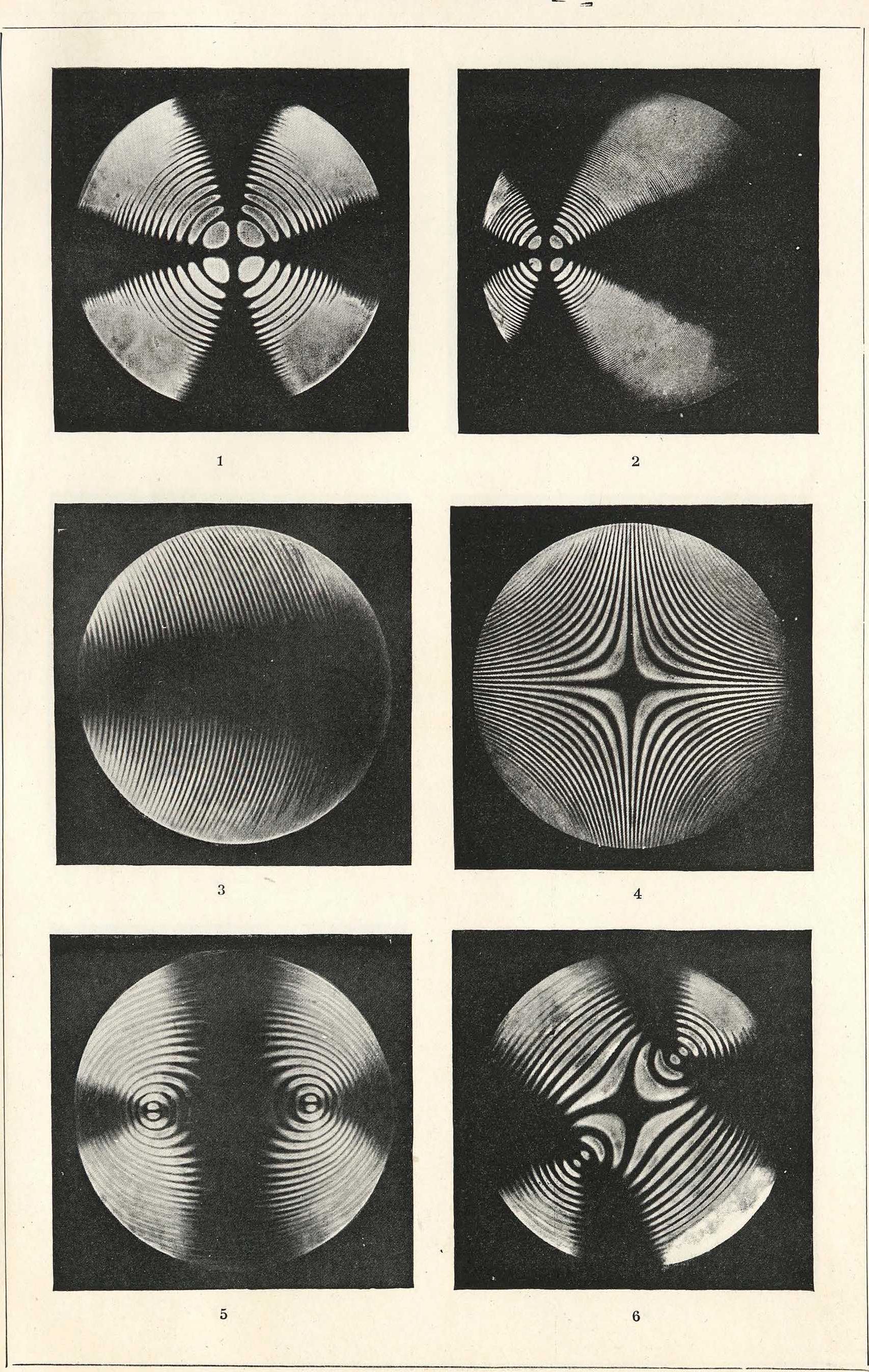
Вид этих поверхностей изображен на фигуре 9 для одноосного и на фигуре 10 для двухосного кристалла. Для каждой разности хода м. б. построена соответствующая поверхность. Сечения семейств таких по верхностей различными плоскостями дают семейство изохроматич. кривых, соответствующих виду интерференционной картины в сходящихся лучах. Для пластинок одноосного кристалла, вырезанных различными способами, получаются т. о. кривые второго порядка: круги, эллипсы, гиперболы и прямые (вкл. л., 1, 2—гисландсмм шпат, пластинка наклонена под углом 80° к оптич. оси; 3—исландский шпат, пластинка под углом 35° к оптич. оси; 4—исландский шпат, пластинка параллельна оптич. оси). При пересечении изохроматич. поверхности двухосного кристалла могут получаться кривые, близкие к равносторонним гиперболам, лемнискатам и кругам (вкл. л., 5—арагонит, пластинка перпендикулярна к средней ли нии между осями, нормальное положение;

6—арагонит, пластинка перпендикулярна к средней линии между осями, диагональное положение; 7—андалузит, пластинка перпендикулярна к одной из оптич. осей).

. Интенсивность в каждой точке интерференционной картины будет зависеть помимо разности хода Δ еще от углов, образуемых плоскостью колебаний падающего луча с главными сечениями пластинки и направлением колебаний, пропускаемых анализатором (ср. выше), вследствие чего наряду с изохроматич. кривыми в интерференционной картине появляются ахроматические изогиры, имеющие вид крестов, гипербол и т. д. Изогиры также могут рассматриваться как линии пересечения нек-рых поверхностей (поверхности изогир). Эти поверхности являются в общем случае конич. поверхностями третьего порядка, проходящими через обе оптич. оси. Для одноосного кристалла поверхность изогир распадается на плоскость и конус второго порядка. При освещении сходящимся светом, поляризованным по кругу, и наблюдении через анализатор, пропускающий лучи, поляризованные по кругу изогиры исчезают, и интерференционная картина становится вполне отчетливой (вкл. л., 8—кварц. пластинка перпендикулярна к оптич. оси; падающий свет поляризован по кругу; проходящий свет выходит через анализатор, пропускающий свет поляризованным по кругу; освещение производилось зеленой линией Hg; 9—арагонит, пластинка перпендикулярна к средней линии; поляризатор и анализатор круговые). Явления хроматич. поляризации в сходящихся лучах чрезвычайно осложняются (при наблюдении в белом свете) вследствие зависимости положения оптических осей в кристалле от длины волны (дисперсия оптич. осей). На вкл. л. приведены фотографии 10, 11, 12 кристалла брукита, вырезанного перпендикулярно к средней линии между осями и рассматриваемого в поляризационном микроскопе между скрещенными нико-лями. На вкл. л., 10 снята при освещении светом с длиной волны 630 τη,μ, 11—610 κημ, 12—583 τημ. Дальнейшие осложнения картины вносятся вращением плоскости поляризации (оптич. активностью кристалла) и дихроизмом. Методы анализа поляризованного света—см. Полярископ.

Лит.: Хвольсон О. Д., Курс физики, т. 2, Берлин, 1923; Stokes О., «The Philosophical Magazine», L., 1852, Series 4, v. 3, p. 316; S о 1 e i 11 et P„ «Α,ηη. de Phys.», P.,1919,t.l2;Winkelmann A., Handbuch d. Physik, B. 2, Abt. 1, Breslau, 1896; Hand-ouch d. Experimentalphysik. hrsg. v. W. Wien u. F. Harms, B. 18, Lpz., 1928; Handbuch d. Physik, hrsg. v. H. Geiger u. K.Scheel, B. 20, B., 1928; UrudeP., I.ehrbuch d. Optik, Lpz., 1906; RosenbuchH.u. W ii 1 Г i n g A., Mikroskopisclie Pkysiographie d. pe-trographisch wichtigen Mineralien, 4 Aufl., Η. 1—2, Stg., 1904—05; H a u s w a 1 d t H., Interferenz-Er-scheinungen im polarisierten Liclit, Magdeburg, 1902, 1904, 1908, Drei Reihen. С. Вавилов.