> Техника, страница 73 > Потенциал

Потенциал

Потенциал в механике, работа силы консервативного поля, совершаемая при переносе материальной точки массы 1 из данной точки ili пространства: в бесконечность. Поле сил называется консервативным, если работа сил при перемещении материальной точки из одного положения в другое зависит только от координат начального и конечного положения (то есть не зависит от пути, по к-рому точка перемещается). Если поле сил задано вектором F=Xi + Yj + Zk

(X, Y, Ζ—функции координат точки поля), а начальное положение М материальной точки характеризуется радиусом-вектором ОМ=r=xi + yj + zk, то П. выразится так:

СО оо

V(M)=J Fdr=J Xdx + Ydy+Zdz.

Μ (χ, у, ζ)

Криволинейный интеграл в правой части по предположению не зависит от пути интеграции; согласно формуле Стокса (смотрите Интегральное исчисление) для этого необходимо и достаточно, чтобы X, Υ, Ζ были частными производными по х, у, ζ от одной и той же ф-ии U (силовая ф-ия):

_v_au ₇_аи

*· вас, ’ ду ’ dz ’ или, что то же самое, чтобы вектор F удовлетворял условию: rot F=0.

Силовая ф-ия отличается от П. только знаком и произвольным постоянным слагаемым: U=— V + С. Сила на единицу массы есть градиент силовой ф-ии: F=grad U. Пример. Сила притяжения центром, находящимся в начале координат, прямо пропорциональна расстоянию. Тогда ,F= — кг

(к— постоянная). Силовая ф-ия U=— ^к^ =

= -*(ж² + 2/^г + 2²).

В механике и физике наибольшее значение имеет ньютоновский П.; он соответствует полю сил, производимому массами, притягивающими или отталкивающими обратно пропорционально квадрату расстояния (можно рассматривать только притягивающую силу, принимая в случае отталкивающей силы массу отрицательной). Если переменная точка М(х, у, ζ) массы 1 находится под действием притяжения точки А(а, Ь,с) с массой т, то сила притяжения по величине равна ~ (к —коэф. пропорциональности, постоянная Гаусса в случае гравитации, г—расстояние AM) и направлена отМк4. Обозначая AM=г, имеем для вектора силы

____ km г _ kmr

7*2 7* т“3

Компоненты F по осям координат имеют выражения:

Х =

hm(x-a)

У-=-

km(y- Ь)

7*3 *

km(z-c)

^3 j

г=γ(χ— α)² + (у — b)² + (г — с)².

Эти компоненты являются частными производными по х, у,ζ от силовой ф-ии

jj _ km _ km

• ^г у" (X - α) 2 -Г(у - Ь) 2 ₊ ( ζ _ с) 2

В дальнейшем самую ф-ию U (предположив к=1) будем называть потенциалом. П. в точке М, происходящий от масс т_ит₂, ., ?%, расположенных в точках А_х. А₂, ., А_к, будет равен сумме П., происходящих от каждой массы” то есть

k

U=2’f - где η·=Λ·Μ.

г=1 ¹

Если масса распределена непрерывно в некотором объёме Ω, имея в точке (а,Ь,с) плотность /г(а,Ь,с), то П. в точке (x,y,z) массы, занимающей элемент объёма dadb dc, имеет выражение:

μ(а,b,с) dadbdc

μ dadbdc

У (χ-α)² +(y-b)² + (z-c)^{2 r} а П. от всей массы выразится интегралом:

(1)

U(x,y,z)=J JJ

μ dadbdc

Здесь U зависит от ж, у, ζ, входящих в качестве параметров в подинтегральное выражение. Непосредственное диференциро-

вание показывает, что £, рассматриваемая как ф-ия от ж, у, ζ, удовлетворяет ур-ию Лапласа:

0* i, e* i. 8» i _п л i а Ш7 + д^г + з^г=° ^{или Δ}?=°-

Всякое решение u(x,y,z) ур-ия Δи=0 назы-вается г а р м о н и ч ес к о и функцией. Применяя к. формуле (1) правило диференци-рования по параметру, находим, что если г не обращается в нуль (вне притягивающих масс), U удовлетворяет ур-ию ΔΕ7=0, то есть П. есть гармоническая ф-ия. Ур-ие U(x,y,z)=С (С—произвольная постоянная) опре делит семейство поверхностей, на которых П. имеет постоянное значение (эквипотенциальные поверхности). Внутри притягивающих масс, хотя подинтегральная ф-ия обращается в бесконечность. при α= ж, b=у, с=ζ, интеграл (1) сохраняет смысл и определяет П.; этот П. внутри объёма Ω удовлетворяет уравнению Пуассона:

AU=— 4πμ(χ ,y,z).

Если масса расположена на поверхности Σ с поверхностной плотностью и, то П. элемента площади da этой поверхности

μ do

имеет выражение, где г — расстояние точки поверхности от точки (ж,y,z) П. всей поверхности Σ:

^U=ffT (2)

Σ

(П. простого слоя). П. простого слоя вне поверхности удовлетворяет ур-ию Лапласа и остается непрерывным при переходе точки (ж,y,z) через поверхность; он имеет на

dUi

поверхности нормальные производные -~ ди_е

и-^— внутреннюю и внешнюю, удовлетворяющие равенству - ψ_η^β=4πμ₀, где

μ₀ — плотность в рассматриваемой точке поверхности, то есть нормальная производная при переходе через поверхность имеет скачок 4л«о; производные в касательных направлениях остаются непрерывными. Наконец если масса расположена вдоль линии L с линейной плотностью μ, то П. этой линии дается ф-лой:

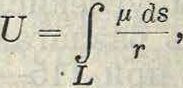
где ds—линейный элемент.

Пример 1. П. поверхности шара радиуса R с постоянной поверхностной плотностью μ имеет выражения: внутри шара

U=4πμβ=-_R, где т—масса всей поверхности; вне шара

jj _ 4πμίί² _ т _#

Т г ’

»—расстояние точки (x,y,z) от центра шара. Внутри шара U—постоянно, его частные производные—нули, следовательно поверхность сферы не притягивает внутренней точки; выражение П. вне шара имеет такой вид, как если бы вся масса m находилась в центре шара.

Пример 2. П. однородного материального шара плотности μ имеет выражения: вне шара

jj 4πμ#³ __ М

внутри шара и=₂Це“- Й=Ц (1-^);

М—масса шара, г—расстояние точки до центра.

Пример 3. П. отрезка оси Z от —А до + А с линейной плотностью 1, если М находится в плоскости ΧΥ. Обозначая расстояние М до начала через г, имеем:

+ А

и

-

-А

dz Ϋζ² + г²

Вычислим силу притяжения; компонента по оси Z равна нулю в силу симметрии, компонента в плоскости XY равна

А о“ — Л

dU _ Г г dz _ _ 1 г _ζ Π _

^ar _у (z*+.r*)‘l^{a r} Lpz² + ^r2J_{z =} _ _t

2 А

г l·⁷ А² + г²

Если материальная линия простирается от

—оо до +со, то

^d/=lim---·Μ==- -²,

^dr Δ =со ] А² + г^{2 г}

то есть бесконечная однородная материальная линия притягивает точку обратно пропорционально 1-й степени расстояния. Из примера 1 видно, что в случае постоянной плотности П. внутри шара постоянный; из электростатики известно, что П. от элек-трич. заряда проводника постоянен внутри проводника; спрашивается, каково в таком случае распределение заряда на поверхности (основная задача электростатики); т. q. требуется найти ф-ию μ на поверхности так, чтобы U=J* j ~ da сохраняло постоянное значение внутри Σ. Эта задача решена Робеном приведением к интегральному уравнению.

Наряду с поверхностным П. простого слоя в математике и физике часто рассматривается П. двойного слоя. Пусть к данной поверхности Σ построена параллельная поверхность Σ на расстоянии ε; элементу da первой поверхности соответствует da’ на второй. На Σ расположены притягивающие массы плотности ρ, на Σ—· отталкивающие плотности ρ, причем выполнено условие: ράσ — ράσ. П. масс на этих двух поверхностях:

Σ Σ

(г и г—расстояния переменной точки поверхности до точки М). Вообразим, что поверхности неограниченно сближаются (ε-i-O), а плотность ρ возрастает до оо, но так, что eg-*μ (конечная величина). Предельное значение U_e есть П. двойного слоя плотности μ:

Σ Σ

^ обозначает производную по положительной нормали к Σ, направленной в сторону положительных масс; <р—угол между линией AM и нормалью AN к поверхности). П. двойного слоя является гармония, ф-ией вне поверхности, при переходе через поверхность претерпевает скачок величины 4πμ₀, где μ₀—плотность в точке перехода. В случае двух независимых переменных х, у ф-ия у [r= V(x - а)·+(у - 6)^а] не удо-

влетворяет ур-ию Лапласа ax2+i^i ⁼ 0, простейшим решением этого ур-ия является, ф-ия In * или In г (логарифмический П. т о ч к и). В этом случае сила притяжения к точке (а, Ь) имеет выражение ^1η-^=-~, то есть обратно пропорциональна 1-й степени расстояния. Механич. интерпр чацию этого закона мы имеем в ньютоновском притяжении точки М(х, у) бесконечною прямою, проходящей через точку А[а, Ь) перпендикулярно к плоскости XY с линейной плотностью j (смотрите пример 3). Аналогично ньютоновскому П. объёма определяется логарифмич. П. площади S

U₁=J¹ J μ(α, b) In г da db

и П. линии L простого слоя U2=f μ In г dS

L

и двойного слоя

L

(φ—угол между AM и нормалью к кривой L). Вне притягивающих масс все эти П. удовлетворяют ур-иям Лапласа, внутри площади S удовлетворяют ур-ию Пуассона ΔΜ=2πμ (ж, у) П_г остается непрерывным на L, но его нормальная производная испытывает скачок 2πμ; U_a при переходе через L имеет скачок Ζπμ.

Ньютоновский П. в пространстве и логарифмич. П. на плоскости удовлетворяют ур-ию Лапласа. Для однозначного определения решения этого ур-ия в данной области надо добавить граничные усло-в и я. Ряд задач физики и гидродинамики (например распределение тепла) приводит к задаче: найти гармония, ф-ию внутри поверхности Σ, если даны ее значения на поверхности (задача Дирихле). Эта задача сводится к нахождению ф-ии и(х, у, z), которая • при заданных значениях на поверхности Σ дает минимальное значение интегралу

Ш«Ш+ (£ί + (ΙΠ

у

V—объём, ограниченный поверхностью Σ (смотрите Вариационное исчисление). Решение задачи Дирихле для сферы радиуса R дается интегралом Пуассона:

и(М)=_4лД J J f(P) (д_{2 + r}a_₂j?rcos VW ^da’

Σ

где f(P)—заданная на сфере ф-ия, d<r—элемент поверхности, г=ОМ, γ= ^ΡΟΜ (О— центр сферы). Из этой ф-лы между прочим следует, что значение гармонич. ф-ии в центре сферы (г=0) равно среднему значению на сфере; т. о. гармоническая ф-ия не может иметь во внутреннней точке ни максимума ни минимума. Для других поверхностей существование решения задачи Дирихле доказано Нейманом, Шварцем, Пуанкаре и др. Аналогично ставится и разрешается задача Дирихле для плоскости. Многие задачи гидродинамики приводят к задаче Неймана: найти гармонич. ф-ию и внутри поверхности Σ, если на границе заданы значения ее нормальной производной ди

^; при этом заданные значения должны удовлетворять условию:

Я ё

Σ

При нахождении решения ур-ия Лапласа в различных системах криволинейных координат (смотрите) получаются специальные функции, например в цилиндрич. координатах ур-ие Лапласа пишется:

д²и 1 ди, 1 д²и, д²и _

+ Г ~дг ^ Г2 δφϊ "Т" Θζ2 ^{_ U} ’

Если искать частные решения этого ур-ия в форме и=β^±λζ ηφ · v(r), то для v(r) получится ур-ие Бесселя:

V +i«+ (А²-^»Я0;

его решения—цилиндрические функции (смотрите Бесселевы функции). Если ввести сферические координаты г, &, φ и искать решения, независимые от φ в форме г^пУ_п(&), то для Υ_η получается ур-ие:

iih£(^Bin*^)+ⁿ<» + ¹)^r-=⁰·

или, вводя переменное х=cos & и обозначая Y_n(&)=Р_п(х),

ур-ие Лежандра; его решения—полиномы Лёжандра, или сферич. ф-ии (смотрите Лежандра полиномы). Если ввести эллиптич. координаты, то аналогично определятся функции Ламе.

Лит.: Аппель П., Руководство теоретической (рациональной) механики, т. 3,М., 1911; Стеклов В. А., Основные задачи математич. физики, ч. 2, П., 1923; Appel Р., Traite de meehanique rationnelle, t. 3, 2 dd., P., 1921, t. 4, -P., 1920; G о u г s a t E., Cours d’analyse mathdmatique, t. 3, 3 dd., P., 1922; Picard E., Traite d’analyse, t. 1, 3 dd., P., 1922; Mlses R. u. Frank P., Differential- u. Integral-gleichungen der Mechanik und math. Physik, T. 1, 7 Auli., Brschw., 1925; Kellog 0., Foundations ot Potential Theory, В., 1929. В. Степанов.

П. электрический, скалярная функция, равная работе переноса в безвихревом элек-трич. поле единицы положительного электрич. заряда из произвольно выбранной начальной точки в точку наблюдения. Т. о. электрич. П. определяется с точностью до произвольной постоянной. В общем случае работа переноса единицы положительного электрическ. заряда вдоль данного отрезка пути L называется электрич. напряжением (смотрите) вдоль этого отрезка и измеряется линейным интегралом вектора напряженности поля JE:

и= jE dr.

ш

Электрич. напряжение, вообще говоря, зависит от пути L. Если напряжение не зависит от пути, то оно м. б. выражено как разность Π. Vа и Vs в начальной точке А и конечной точке В этого пути:

u=V_A-V_B. (2)

В этом случае вектор напряженности электрич. поля JE является отрицательным градиентом Π. V:

Е- — grad V. (3>

Т. о. вектор Έ направлен перпендикулярно к поверхностям уровня (поверхностям постоянного значения Π. V) в сторону убывания П. и равен по абсолютной величине возрастанию П. при перемещении на единицу длины вдоль силовой линии. Электрич. поле характеризуется не абсолютным значением П., а разностью П. Поэтому неверно утверждение, все еще встречающееся иногда, будто П. служит мерою электрич. состояния тела. В частности расхождение листочков электроскопа зависит не от П., сообщаемого листочкам, а от разности П. между листочками и стенками электроскопа. Вычисление П. имеет большое значение для графического и аналитического определения поля. В электростатич. поле П. удовлетворяет диференциальному ур-ию Лапласа

V²F=0 (4)

во всех точках, где отсутствует электрич. заряд. В тех областях, где имеются электрич. заряды, П. удовлетворяет диференциальному ур-ию Пуассона

v²r=-4> <⁵>

где g—плотность заряда в данной точке, ε—относительный диэлектрич. коэф. среды и «о—диэлектрич. коэф. вакуума. В электро-статич. системе CGS %=^, в международной системе (V выраженов V, g—в С/сл³> «ο=0,885 · 10~¹³ F/см. Для интегрирования этих диференциальных ур-ия требуется знать пограничные условия, то есть значения V и его производных на поверхностях, ограничивающих поле. В электро-статич. поле П. сохраняет постоянное значение на поверхности и внутри каждого однофазного проводника. Интегрирование ур-ий (4) и (5) при заданных П. на поверхности проводников только в простейших случаях приводит к обычным алгебраич. функциям. В более сложных случаях интегрирование ур-ий (4) и (5) представляет большие затруднения. На практике часто прибегают к графич. определению поля или к приближенным методам интегрирования.

• Кроме того применяется целый ряд экспериментальных методов. В случае двухмерного (плоскопараллельного) поля П. может быть определен во многих случаях методом конформных отображений.

Если известно распределение зарядов во всем пространстве, то П. определяется по формуле

V =

Voo (S) (S_a) )

,(6)

где Q—плотность объёмного заряда в элементе объёма dr, а—плотность поверхностного заряда на элементе поверхности dS, η—момент двойного слоя (произведение из абсолютной величины плотности заряда по обе стороны поверхности двойного слоя на расстояние между этими слоями), άΩ—элементарный телесный угол, под которым виден из точки наблюдения элемент поверхности Sj двойного слоя, обладающий моментом ту, г—расстояние от точки наблюдения до данного элемента поверхности или объёма.

П. магнитный, скалярная функция, численно равная работе переноса в безвихревом магнитном поле единицы положительного (фиктивного) магнитного заряда из точки наблюдения в бесконечность. Магнитное напряжение, или разность магнитных П., между точками А и В равна линейному интегралу вектора напряженности магнитного поля

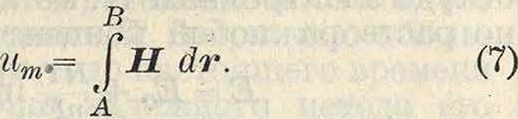
По закону полного тока (смотрите Токи электрические) ясно, что вектор Ή имеет П. только в тех областях, где плотность· тока δ — 0. Там, где 5^0, не существует магнитного П. Магнитный П.—многозначная ф-ия, т. к. магнитное напряжение вдоль замкнутой линии, охватывающей ток I, возрастает на I при каждом обходе этой линии. Разность магнитных П. измеряется при помощи пояса Роговского (смотрите Электрические измерения). Во многих случаях магнитное поле определяют при помощи векторного II., или векторпотенциал а, А по ур-ию

В=rot А, (8)

причем в стационарных или квазистацио-нарных полях на этот вектор налагают еще добавочное условие

div А=0.

Векторпотенциал удовлетворяет во всем поле векторному ур-ию Пуассона

²Α=— μμ о <5, (9)

где δ—плотность полного тока. Если известно распределение плотности тока в пространстве, то векторпотенциал определяется по аналогии со скалярным П. при помощи интеграла

А =

μ/jQ Г* όάτ

4π J г

(10)

со где μ—относительный коэф. проницаемости среды, до—коэф. проницаемости вакуума. Напряженность магнитного поля определяется т. о. из ур-ия а“

Л г [аг] 4i J гЗ

dr, (11)

со со где вектор г берется в направлении от элементов объёма с плотностью тока <3 к точке наблюдения. Если поле создается линей ными проводниками, для которых справедливо соотношение

Idr=S dr,

где I—сила тока в проводнике, a dr—элемент его длины, то выражение для магнитного поля Ή, создаваемого п контурами Κ_λ, по которым проходят токи Ι_λ, принимает следующий вид:

Η ί¹ I, fV· (I²)

;.=ι (κ_λ)

Элементарное выражение этой ф-лы дает известный закон Био-Савара

<Ш=UJrrJ ₍₁.3)

Г 3

или в скалярной форме

(1Н=——0—> (130

где dl—элемент длины проводника, а—угол между этим элементом и радиусом-вектором г, соединяющим элемент длины с точкой наблюдения. При помощи векторпотенциала поток магнитной индукции определяется в виде линейного интеграла

Ф=j"В dS=J’ rot AdS= A dr,

(S) (S) (К)

где S—поверхность, окаймленная контуром

К. В случае нестационарных явлений, когда приходится учитывать скорость распространения электромагнитного поля, обыкновенные П. заменяются запаздывающими, или ретардированными, П. (смотрите Электромагнитные волны).

Лит.: Круг К. А., Основы электротехники, 2 изд., М., 1926; Тамм И. Е., Основы теории электричества, т. 1, М.—Л., 1929; Шпильрейн Я. Н., Векторное исчисление, М.— Л., 1925; М и т-кевич В. Ф., Физические основы электротехники, ч. 1, М.—Л., 1928; Abraham М. u. Becker R., Th oried.Elektrizitat.B. l,Lpz.—Β·, 1930; Mises R. и. Frank Р., Differential- и. Integralgleichunsen d. Mechanik und mathematischen Physik, 7 Aufl., Band 1, Braunschweig. 1925; Hague B., Electromagnetic Problems a. Electrical Engineering, Oxford, 1929. Я. Шпильройн-

П. электродный, разность потенциалов, образующаяся на границе металл—раствор при погружении пластинки из металла в раствор, содержащий ионы этого металла. Согласно формуле Нёрнста значение электродного П. металла определяется выражением

ε

RT

nF

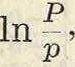
(1>

где ξ—электродный П. в V, R—тазовая постоянная в J, Т—абсолютная темп-pa, п— валентность иона, F—число Фарадея, Р— т. н. электролитич. упругость растворения металла, р—осмотич. давление ионов данного металла в растворе. Как видно из ф-лы (1), величина электродного П. при данной t° зависит от химич. природы металла (последняя определяет значение электролитической упругости его растворения и валентность) и от концентрации ионов металла в растворе, так как осмотич. давление р, как известно, пропорционально концентрации. Величина электролитич. упругости растворения служит мерой стремления металла переходить в раствор; у металлов неблагородных (щелочные и щелочно-земельные, Zn, Μη) она велика, наоборот, металлы благо-

родные (Pt, Au, Ag, Си) обладают ничтожно малой величиной упругости растворения. Величина электродного П. обычно определяется относительно какого-нибудь электрода, П. которого условно принимают равным нулю. Обычно таким электродом является нормальный водородный электрод, к-рый состоит из платиновой пластинки или платиновой проволоки, покрытой платиновой чернью и погруженной в раствор кислоты с нормальной концентрацией Н ионов, через который пропускают ток водорода под атмосферным давлением. Такой электрод ведет себя так, как если бы он был сделан из металлически проводящего твердого водорода. Для экспериментального определения электродного П. какого-нибудь металла составляют цепь из исследуемого электрода и нормального водородного электрода и определяют эдс этой цепи компенсационным методом Поггендорфа; полученное значение эдс и принимают за величину электродного П. данного металла. На практике пользуются при определении электродного П. не водородным, а так называемым каломельным электродом, т. к. манипулировать с ним гораздо удобнее. Полученное значение эдс пересчитывают затем на водородный электрод. Если концентрация ионов металла в растворе равна единице (1 з-ион на 1 л), то значение электродного П. называется нормальным П. данного металла. Значение нормальных потенциалов приведено в следующей таблице.

Ряд напряжений некоторых химических элементов по отношению к нормальному водородному электроду <ε^=0,0Y) при концентрации электролитов 1,0 N и t° 20°.

	>		>
Электрод	4« §3 к	Электрод	i"
			И&
Катионы		Катионы
Li!Li*.	-3,02	Η22Η·.	+0,02
К|К*.	-2,92	Со Со".	+0,34
Na! Na’.	-2,71	Си Си“.	+0,51
Mg|Mg".	-1,65	Fe[Fe’".	+0,72
ZnjZu".	-0,76	AgiAg*.	+0,80
Cr|Cr“.	-0,6	2Hg Hg2” · ·	+0,8
CriCr"·.	-0,53	HgjHg".	+0,86
FejFe".	-0,43	Au|Au*.	+ 1,6
Cd Cd". ТЦТГ.	-0,40 -0,33	Анионы
CoiCo".	-0,29	S|S ТВ.	-0,55
Ni| Ni*.	-0,22	2J J2 ТВ.	+0,54
PbPb·*.	-0,12	2Br Br2 Ш.	+ 1,08
Sn|Sn“.	-0,10	2C11C12 газ.	+ 1,36
Fe!Fe".	-0,04	2F,F2ra3.	+ 1,9

В вышеприведенной таблице указаны потенциалы не только металлов, но и нек-рых металлоидов. Приведенные выше рассуждения целиком распространяются и" на них, разница заключается лишь в знаке, к-рый надо поставить перед ф-лой (1). Для-потенциала металла мы пишем р’

(1)

имея в виду, что в случае, если электроли-тич. упругость растворения металла больше осмотич. давления ионов в растворе, металл будет посылать свои ионы в раствор и вследствие того, что ионы металла заряжены по- I ложительно, пластинка металла зарядится I

отрицательно. Для металлоида мы следовательно должны написать

*-+£*£

(1")

где все величины аналогичны таковым в ур-ии (1). Газовые электроды (например хлорный) осуществляются аналогично водородному. Из значения нормального потенциала легко получить значения П. металла относительно раствора любой концентрации его ионов. Действительно из ф-лы (1) имеем

^Р (2)

- кг.

^ЕГ-ш^1пТс’

ибо осмотическое но концентрации давление пропорциональ-С ионов металла или кг, р

^E-~nF^lnk·

RT

nF

In С.

(3)

В том случае, когда концентрация ионов металла равна единице, то есть когда мы имеем дело с т. н. нормальным П. металла, второй член равенства (3) обращается в нуль, следовательно величина нормального потенциала металла Е₀ м. б. представлена следующим образом:

Е₀=-

RT, р гГ 1П, > nF k

откуда электродный П. металла относительно раствора любой концентрации ионов

Е=Е₀ + —Jr In С;

или, заменяя постоянные их числовыми значениями и переходя к десятичным логарифмам, имеем для комнатной Г (18°)

E=S„ + ⁰’“⁵⁸lgC.

Как видно из ф-лы, электродный П. тем выше (благороднее), чем выше концентрация ионов металла в растворе, причем изменение концентрации сказывается на величине электродного П. сравнительно незначительно; при увеличении концентрации в 10 раз значение П. возрастает всего лишь на 0,058

V в случае 1-валентного металла и на 0,029

V в случае 2-валентного!

Приведенная выше таблица нормальных потенциалов известна под названием ряда напряжений. Пользуясь им, можно определить эдс любого гальванич. элемента, эдс которого определяется, как известно, разностью электродных потенциалов, например для эдс элемента Даниэля Си CuS0₄ ZnS0₄ Zn в случае нормальных концентраций ионов Си“· и Zn" Е=0,34 — (—0,76)=1,1 V. Этот ряд представляет количественную характеристику известной закономерности, по которой неблагородные металлы вытесняют благородные из их солей; известно, что железная пластинка при погружении в раствор медного купороса выделяет из него медь по ур-ию Fe+CuS0₄=FeS0₄+Cu; возможность такого рода реакции электрохимически легко объясняется тем, что на поверхности железной пластинки в этом случае появляется коротко замкнутый гальванич. элемент, одним полюсом которого служит железо, другим—медь; т. к. электродный П. железа ниже (менее благородный), чем меди (—0,43 и +0,34), то железо будет в этом случае растворимым электродом (анодом), а медь—катодом, в силу чего железо будет переходить в раствор, а медь выделяться в свободном виде. Эти же соображения справедливы и для выделения водорода. Металлы, стоящие выше водорода в ряду напряжений (менее благородные), выделяют его из к-т, стоящие же ниже (более благородные) не выделяют, а, наоборот, газообразный водород восстанавливает растворы их солей до металла. Явления, связанные с различной величиной электродного П. металлов, лежат в основе процессов разрушения, или т. н. коррозии (смотрите) металлов. Значение электродного П. принимается всегда во внимание при защите одних металлов другими, хотя в нек-рых случаях данные ряда напряжений не вполне соответствуют действительному поведению металла вследствие осложнений, вызываемых процессами окисления и паствирования (смотрите). Последнее время в практике значением электродного П., измеренного на опыте, часто пользуются для •определения концентрации; на этом основано определение концентрации водородных ионов (смотрите) и электролитическое титрование (смотрите). Во всех приведенных рассуждениях были приведены лишь относительные. значения электродного П., отсчитанные от нормального водородного электрода, каковому был условно приписан П., равный нулю. Определение абсолютного значения электродного П. сопряжено с большими трудностями, и до настоящего времени нет еще достаточно надежного метода его определения. Из предложенных методов наибольшее согласие между собой дают методы электрокапиллярной кривой и ртутного капельного электрода. Согласно этим методам абсолютное значение потенциала нормального водородного электрода лежит между —0,22 и —0,27 У. Другие методы дают сильно отклоняющиеся от этих значений цифры. Напр. метод Бенневица и Шульца с серебряными электродами в растворе AgN0₃дает для потенциала нормального водородного электрода значение, равное +0,485V, так что вопрос об абсолютной величине электродного П. не может считаться окончательно разрешенным, вследствие чего на практике приходится иметь дело исключительно с относительными значениями. В некоторых учебниках, правда, даются величины абсолютных значений электродного П., высчитанные по капельному электроду, но следует отметить на основании сказанного выше, что определенный таким образом электродный Р. любого металла на 0,27 V больше обычно указываемого П. относительно водородного электрода.

Лат.: Э г г е р т Дж., Учебник физич. химии, пер. с нем., етр. 445—489, М.—Л., 1931; Изгарышев Н. А., Электрохимия и ее технич. применение, стр. 58—102, Л., 1929; Леблан М., Руководство по электрохимии, пер. с немецкого, стр. 190—341,М.—Л., 1930; G г и b е Grundziige der theoretischen u. an-gewandten Elektrochemie, 2 Auli., p. 65—110, Lpz., 1930: E u k e n A., Lehrbuch der chemischen Physik,

3 Auil., p. 497—522, Lpz., 1930; FoersterF., Elek-trochemie wasseriger Losungen, Handbuch d. angewand-ten physikalischen Chemie, hrsg. v. G. Bredig, B. i,

4 Auil. p. 147—239, Lpz., 1923. С. Ппетенев.

П. термодинамический, термодинамическая функция Θ (х, у), определяющая при заданных условиях возможность любого физикохимического процесса в данной системе, то есть условие его необратимости, а также условие обратимости процесса, условия равновесия и его устойчивости (см“. Равновесие, Термодинамика). П. термодинамические (Θ) обладают следующими основными свойствами, весьма ценными для решения практических задач.

1) При данном выборе параметров, поддерживаемых постоянными, условие возможности процесса дается условием возрастания (άθ > 0) или убывания (άθ < 0) термодинамического П.

2) Условия устойчивого или неустойчивого равновесия определяются максимумом или минимумом термодинамического П. (при άθ=0; d²6^0); условия безразличного равновесия будут άθ=0; ά²θ=0.

3) При определенных условиях (например в изотермич. или изоэнтропич. процессах) убыль термодинамич. П. измеряет максимальную работу данного обратимого процесса А_т=(Θ, — θ₂). Для необратимых же процессов Α_η<(θ₁ — θ₂).

4) П. термодинамич. системы дает ее полную термодинамич. характеристику. Зная термодинамич. П., можно вычислить все ее

I термодинамич. функции состояния и найти ур-ие состояния ее.

Из общего выражения I и II начал термодинамики (обозначения см. в таблице):

TdS>dU + %Xdx (ϊ)

η

находим, что при выборе постоянными параметрами всех х и U или всех×и ф-ии U + ^Хх=Н энтропия S является ф-ией,

Таблица термодинамических потенциалов.

Параметры	Вид потенциала		Условия устойчивого равновесия
U, v (х)	Функция, определяющая равновесие и не являющаяся П.	1 Энтропия S	Максимум
я, V (X)
- Т, V (X)	Изотермические потенциалы	F=U-TS—внутренний П. (свободная энергия)	Минимум
Т, p (X)		<t>=U-TS+pv—полный П. или v>=S—~ (функция Планка)	Минимум Максимум
S, v (х)	Изоэнтропичес-кие потенциалы	U—внутренний П. (полная внутренняя энергия)	Минимум
S, V (X)		Н=U+pv—полный П. (тепловая функция, энтальпия)	Минимум

определяющей условия возможности процессов (dS>0), обратимости (dS= 0) и устойчивого равновесия (dS= 0; d²S<0, S=max). При этом

(& _ 1		1 -z
dU]x T’	[dxj	h τ

2×dx—сумма обобщенных работ (X может быть например некоторым напряжением, а dx—соответствующей деформацией и т.д.). В дальнейшем для ясности примем Х=р, x=v и 2 работе расширения.

S не имеет размерности термодинамич. П., не обладая свойством (3), а потому выделена отдельно в таблице.

П. термодинамические м. б. разделены на 2 класса. а)ИзотермическиеП. Одним из (п +1) постоянных параметров является теМп-ра Т (системы Т, х или Т, X). В первом случае из (1)

TdS^dU + dA

находим: dA< — dF_T и П. термодинамич. F=U—TS называется свободной энергией, так как максимальная работа (в изотермическом обратимом процессе) измеряется убылью F, или внутренним изотермич. П. При этом

dF (v,T)=— p dv — S dT, τ. e.-[«q^] -ρί,Τ) (ур-ие состояния данной молекулярной системы), — ⁼ ^

(исключение энтропии заменой ее темп-рным коэф-том изотермич. П. термодинамического). Кроме того dF

U=F — (ур-ие Гиббса-Гельмгольтца).

Во втором случае (при параметрах Τ, X, например Т, р) термодинамического П. является функция:

Ф =U — TS + ρυ, (2)

т. к. из (1) при этом

d(U-TS + pv)<0;

Ф называется полным и з от ерническим П. Из (2)

άΦ (р, Τ)=V dp — S dT

находим выражения остальных ф-ий через полный изотермич. П.:

V (р, Т)=

дФ ς, _ дФ

~др^{9 ύ} ~ ~дТ

H=(U+ ρυ)=Φ-Τ~·

Для теплоемкости также имеем симметричные выражения:

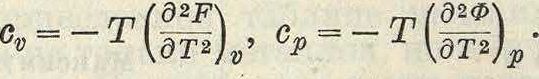
Условия возможности процесса dF<0 или йФ< 0, условия устойчивого равновесия d²F>0 или ά²Φ> 0 (минимум П.).

б)ИзоэнтропическиеП. Одним из (п +1) постоянных параметров является энтропия S (системы S, х или S, X). В первом случае из (]) находим:

dU <Т dS — δ А; δ А < — dU_s;

термодинамическим П. является U=f (S, v). При этом

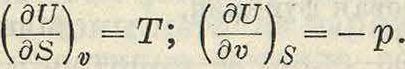
Во втором случае

dH <Т dS + vdp

и при параметрах р, S, II=U + pv=f (p, S) является термодинамич. П.

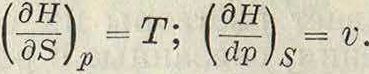
Изоэнтропические термодинамические П. обладают тем свойством, что в процессах х=Const и×= Const измеряют тепловой эффект процесса, то есть являются тепловыми ф-иями:

Сq—выделенное в процессе тепло).

Химическим П. называется производная термодинамич. П. по массе данного компонента к системы

При постоянстве остальных параметров (кроме масс тонн) изменение термодинамич. П. сводится при химических реакциях к одной только «химической работе»:

de=2 Pkdm_k. к

Условие

άθ=2 /T^dmi=о (3)

к дает общий закон динамич. равновесия всех физико-химич. и химич. процессов. При распределении данного компонента к между п фазами условие равновесия (3) сводится к (η — 1) условиям:

(«4=(Л)₂= ··=0V)»’ <⁴>

ведущим к правилу фаз (смотрите). При переходе одного компонента из одной фазы (1) в другую (2) условие равновесия (4) принимает вид: Д1=μ₂, а условие перехода 1->2—вид: μ_λ — д₂ > 0. См. также Окклюзия, Плавление,

Пары.

Общая зависимость между изотермическим Π. θ_τ и соответствующим ему изоэнтро-пическим П. S_s:.

θχ — Θ,

двт

~дт

Общая зависимость между внутренним (0<> и соответствующим полным θ₀ термодинамическим П.:

где 2%-1^хк ⁼ θ_β—внешний П., то есть П. постоянных внешних сил, сводящийся в простейшем случае к П. постоянного внешнего давления р:

S_e=p-v. _ __

“Лит.: Б"а"ндт“аГА-Г" Основания термодина-

мини, 4 изд., М.—П., 1923; П ланк М., Термодинамика, пер. с нем., М. — Л., 1925; П о с а л ь с к и и Π. Т., Равновесие соприкасающихся масс, Одесса, 1895; Вознесенский С. А. и Ребиндер ГГ. А., Руководство к лабораторным работам по фи-зич. химии, М.—Л., 1 928; Богуславский С. А., Основы могекулярной физики и применение статистики к вычислению термодинамич. потенциалов, «Научные известия», сб. 3,Физика, М., 1922; Умов Н.А., «Bull, de la Socidtd Natural.», M., 1894, 2; Massieu, «CR», 1869, v. 69, p. 858, 1057, «journ. de Physique», P., 1877, v. 6, p. 316; Gibbs J. W., Thermodyna-misehe Studien, Lpz., 1892; D u h e m P., Trait6 denergetique ou de thermodynamique g6n6rale, t. 1—2, P., 1911 — 12; Duhem P., Trait6 610mentaire de m6-canique chimique, fondee sur la thermodynamique, t. 1—4, P., 189 7—99; DuhefflP., Le potentiel ther-

modynamique, P., 1 886; Helmholtz H., Die Ther-modynamik chemischer Vorgange, «Sitzungsber. Preuss. Akad.», B., 1882; Helmholtz H., Abhandlungen zur Thermodynamik, Ostwalds Klassiker, B. 124, Lpz., 1921; V a n-L a a r J., Sechs Vortrage iiber d. thermodynamische Potential, Lpz., 1906; Lewis <3·. N., Thermodynamik, W·, 1927; Schottky W., U 1 i ch H. u. W a gn e r G-,Thermodynamik, B.,1929; Voigt W-, Lehrbuch der Kristallphysik, Lpz.—B., 1928. П. Ребиндер.