Правило фаз

Правило фаз, единственное широкое обобщение в учении о равновесии гетерогенных систем, оказавшее химии неисчислимые услуги, позволившее исследовать и классифицировать чрезвычайно обширный и сложный комплекс явлений химич. равновесий. П. ф. в настоящее время -вышло из стадии теоретич. интереса и вплотную вошло в ряд прикладных наук: галургию (изучение солей в широком смысле этого слова), металлургию, технику перегонок и т. д.

Π. φ. было открыто И. В. Гиббсом и опубликовано им в Transactions of the Connecticut Academy в 1876—1878 гг. в знаменитой статье, посвященной равновесию в гетерогенных системах. Изложенная в высшей от· пени абстрактно, эта работа Гиббса впервые была истолкована Ван-дер-Ваальсом и приложена к опытным явлениям Розебумом в 1887 г. В 1807 г. появилась монография Ванкрофта «Правило фаз» и первое систематич. изложение как самого П. ф., так и его приложений. Знаменитые работы Вант-Гоффа по химии стассфуртских отложений открыли П. ф. путь в прикладные науки.

Понимание П. ф. и практич. пользование им требует ознакомления с рядом предварительных понятий. Состоянием системы называется совокупность всех ее свойств; свойства же системы на математич. языке называются ее переменны ми. Каждая система имеет строго определенное число независимых переменных; остальные переменные (свойства) являются ф-иями избранных независимых переменных. Сколькими независимыми переменными определяется состояние системы—показывает опыт. Выбор же свойств в качестве независимых переменных определяется удобством при решении задачи; с математич. точки зрения любое свойство системы м. б. взято за независимое переменное; с опытной же точки зрения удобнее брать для этой цели те свойства, которые легко измерять. В большинстве случаев выбор падает на абс.темп-ру Т°, давление р (или объём V) и концентрации веществ о_г, с₂, е₃, ., составляющих систему. Из обширной группы свойств системы мы выделяем группу термодинамич. свойств; это те свойства, которые являются ф-иями Т°, давления (или объёма), концентраций и теплосодержания (и только этих величин). К термодинамическим свойствам принадле-. жат термин, и калорич. коэф-ты, внутренняя энергия, энтропия, потенциалы и т. д. Такие свойства, как диэлектрич. постоянная, показатель преломления, вращение плоскости поляризации, являются физическими, а не термо динамич. свойствами. Изменение всякого вида энергии м. б. представлено произведением интенсивности (силы в обобщенном смысле) на изменение фактора емкости, например работа расширения pdV есть произведение интенсивности (давления) на изменение фактора емкости (объёма); прирост электрич. энергии Εάη выражается произведением интенсивности (электрического потенциала Е) на изменение фактора емкости (количества электричества η) и т. д. При составлении общей системы из нескольких систем всегда можно поставить опыт так, что фактор емкости общей системы будет суммой факторов емкости отдельных составляющих систем (например V=V₁ + V_i+., n=Vi + %+.); факторы же интенсивности не складываются, а при достижении равновесия выравниваются (так, при составлении системы выравниваются давления, электрич. потенциалы и тому подобное.). Это выравнивание интенсивностей есть следствие второго принципа энергетики. Прирост тепловой энергии dQ мы также с формальной точки зрения можем представить в виде произведения Xdx, где -X—интенсивность, способная выравниваться в составной системе, а х—фактор емкости; в данном случае Х=Т°, фактор емкости—· энтропия системы S; тогда d.Q=TdS. Энтропии систем при их составлении в общую си- стему могут складываться (обратимые процессы). Энтропия с опытной точки зрения обладает тем крупным неудобством, что она не поддается прямому измерению подобно объёму или количеству электричества. Очевидно, что изменение запаса химич. энергии также м. б. представлено произведением Xdx, причем здесь массы m веществ являются факторами емкости, т. к. они складываются при составлении общей системы из частных; фактор же интенсивности химич. энергии нам неизвестен; мы называем его химическим потенциалом μ, и тогда изменение химич. энергии можно представить в виде произведения μάνι. Химический потенциал обладает с опытной точки зрения тем крупным неудобством, что мы не умеем его измерять подобно давлению, электрич. потенциалу, Т°. Большие трудности, которые встречаются при понимании, усвоении и применении химич. термодинамики, в значительной степени коренятся в экспериментальном неудобстве—нашем неумении измерять такие важные факторы, как энтропия и химич. потенциал;, вследствие этого мы не можем их оставлять в конечных формулах (подобно объёму, массе, электрич. потенциалу и т. и.); мы пользуемся этими понятиями в ходе рассуждений, но последние мы должны вести до тех пор, пока эти понятия не исчезнут в конечном результате.

Рассмотрим систему, состоящую из насыщенного раствора соли, твердой соли, лежащей на дне сосуда, и пара над раствором. Каждая часть системы, отделенная друг от друга видимой поверхностью раздела, называется телесным комплексом. Пар, раствор, каждый отдельный кристаллик соли—телесные комплексы. Телесные комплексы, обладающие одинаковым химич. составом и одинаковыми термодинамическ. свойствами, называются фазой систе-м ы. В данном примере для пара и раствора понятия телесных комплексов и фаз совпадают, все же кристаллики соли образуют одну твердую фазу (донную, лежащую на дне); т. о. наша система состоит из трех фаз: парообразной, жидкой и твердой. Если система представляет раствор, насыщенный винной к-той, пар и на дне—смесь право- и левовращающих кристаллов винной к-ты, то здесь мы имеем четыре фазы: парообразную, жидкую и две твердых. Винная к-та вращает плоскость поляризации как в твердом виде, так и в растворенном; это вращение есть свойство самой молекулы винной к-ты, то есть химич. свойство; право- и левовращающие кристаллы винной кислоты отличаются химически, а потому они должен быть отнесены к разным фазам. Βίο если взять раствор, насыщенный хлорновато натриевой солью, пар и на дне—смесь право- и левовращающих кристаллов этой соли, то здесь имеем только три фазы: парообразную, жидкую и одну твердую. Дело в том, что хлорноватонатриевая соль вращает плоскость поляризации только в твердом состоянии, но не в растворенном. Это вращение не есть свойство молекулы, а результат укладки молекул в кристаллич. ячейке; это не химич. свойство, но и не термодинамическое; следовательно оба вида кристаллов должен быть отнесены к одной твердой фазе.

Составляющими вещества-м и системы называются те вещества ее, которые м. б. выделены из системы и могут существовать вне ее в изолированном виде. Если система представляет раствор хлористого натрия в воде, то здесь мы имеем два составляющих вещества: хлористый натрий (NaCl)n воду. Ионы Na" и C1—не составляющие вещества, т. к. они порознь не м. б. выделены из раствора. Вода—равновесная смесь троякого рода молекул: Н₂0, (Н₂0)₂и (Н₂0)₃, но эти виды воды не м. б. выделены порознь, между ними чрезвычайно скоро устанавливается равновесие; составляющим веществом называется равновесная смесь этих молекул, называемая просто водой и обозначаемая символом Н₂0. В растворе хлористого натрия оба составляющие вещества—вода и NaCl—независимы друг от друга: изменение количества одного из них не изменяет количества другого. Такие системы, в которых составляющие вещества независимы друг от друга, называются с и-стемами первого класса;в них протекают физич. и физико-химич. процессы, но не химические. Возьмем систему, состоящую из Н₂0, NaCl, КС1, Na₂S0₄ и K₂S0₄. Здесь 5 составляющих веществ, но они не независимы друг от друга, т. к. в силу реакции 2 NaCl+K₂S0₄ 2 KCl+Na₂S0₄изменение количеств одного из этих веществ влечет за собою изменение количеств и трех других веществ; мы имеем пять составляющих веществ и одну связь между ними, следовательно независимых составляющих веществ— четыре. Если в этой системе при определенных t° появится новое вещество Na₂SO₄-10 Н₂0, то тогда будет 6 составляющих веществ", но налицо новая связь, даваемая ур-ьем превращения декагидрата: Na₂SO₄-10H₂O Na₂S0₄+ ЮН₂0, следовательно независимых составляющих веществ по прежнему четыре. Системы, в которых протекают химич. реакции и в которых общее число составляющих веществ больше числа независимых составляющих веществ, называются системами второго к л а с с а. Независимые составляющие вещества в системе называются ее компонентами. Число компонентов определяется числом составляющих веществ минус число связей между последними. С помощью компонентов м. б. выражен состав любой фазы системы, находящейся в равновесии. Поэтому числом "компонентов называют также наименьшее число веществ, при помощи которых можно выразить состав фаз системы. Определить число компонентов обыкновенно очень нетрудно. Какие вещества взять в качестве компонентов, по существу безразлично; выбор определяется удобством: выбирают такие вещества, при помощи которых состав любой фазы м. б. выражен без применения отрицательных количеств. Напр. в системе, в которой возможна реакция СаСОз ^ СаО+С0₂,

двакомпонента и три фазы (СаС0₃, СаО и газообразная С0₂); если в качестве компонентов возьмем СаО и СО ₂, то третья фаза выразится суммой компонентов СаО + С0₂, если же в качестве компонентов возьмем СаС0₃ и С0₂, то состав третьей фазы СяО =СаСОз-СС>2·

Не всегда однако возможно избежать применения отрицательных количеств, так, в приведенном выше примере это невозможно.

В ы в о д П. ф. требует предварительного установления ограничительных условий. Мы принимаем, что телесные комплексы не настолько малы, чтобы нельзя было говорить о постоянстве их Т° и давления со стати-стич. точки зрения и что их поверхностная энергия не оказывает заметного влияния на свойства системы; этим мы исключаем коллоидные растворы из области, к которой применимо П. ф. Далее, мы исключаем действие различных сил, кроме давления, и рассматриваем системы таких размеров, что можно не считаться с различиями в действии силы тяжести в различных ее местах. В этих условиях факторы емкости (объём, энтропия и массы компонентов) всей системы равны суммам соответствующих факторов емкости отдельных фаз. Как следствие второго принципа термодинамики и постулатов о равновесии вытекает условие равновесия гетерогенных систем: равенство факторов интенсивности фаз в системе. Берем указанные выше обозначения для давления, темп-ры и химич. потенциала компонента; индекс вверху символа указывает номер фазы, индекс внизу—номер компонента; пусть всех фаз в системе—к, компонентов—п. Тогда условия равновесия выразятся так:

Р _ р" =. .,	=ρ(*) 1
гр _β rp/r	=ΤΑί
= К=· · ·	• =/»φ Ι
⁼ 1*2 ⁼ · · ·	•=π© ι,
№η⁼ Ρη “ · · ·	= μ&) i

то есть для равновесия гетерогенной системы необходимо равенство давлений, темп-p и химич. потенциалов компонентов в ее фазах. В качестве независимых переменных берем давление, Т° и концентрации; след, условия (1а) суть тождества, а условия (16) дают

n(fc-l) ур-ий, т. к. μ=f(p, Т°, с_и с₂.с_м).

В каждой фазе подлежат определению и—1 концентраций, так как п-я концентрация по смыслу понятия о концентрации м. б. найдена из выражения

^С1 + ^С2 + ··· + ^Ся-1+^Ся=1·

Т. о. число всех концентраций, подлежащих определению, равно к(п — 1). Рассматривая независимые переменные как неизвестные, мы получаем всех неизвестных (концентрации, давления и темп-ры) к(п — 1) + 2, а число ур-ий, решением которых эти неизвестные м. б. найдены, равно п(к — 1). Т.к. для получения определенного решения ур-ия число ур-ий должно или равняться или быть меньше числа неизвестных, то n(fc-l)s= к(п-1) + 2,

или к^п + 2, (2)

т.е.:число фаз в гетерогенной системе, находящейся в равновесии, равно или меньше числа компонентов плюс два. Это и есть знаменитое правило фаз Гиббса. Чтобы уничтожить знак неравенства, выражение (2) можно переписать так:

F=n+2—k. (2а)

Величина F, равная разности между w+2 и числом фаз, называется числом степеней свободы данной системы.

Т. Э. m. XVII.

Если п+2=к, то jF=0, система не имеет степеней свободы, она инвариантна: это значит, что мы не можем изменить значения ни одной из независимых переменных (р, Т°, С{) без того, чтобы не изменилось число фаз в системе. Если п + 2 > 7с, то системы имеют степени свободы; при к=п+1, ff=l, это значит, что одну из независимых переменных, например Т°,мы можем менять по произволу (в определенных пределах), без того чтобы число фаз в системе изменилось; такая система называется м о н о в а-риантной. При к=п, F= 2 система дивариантн а,—две ее независимые переменные мы можем менять по произволу без изменения числа фаз в системе, и т. д. При выводе П. ф. мы предполагали, что все вещества системы находятся во всех фазах ее; следовательно в системе, в которой идет реакция восстановления окиси железа окисью углерода (FeO-f СО ^Fe + C0₂), мы допускаем, что в газообразной фазе присутствуют, хотя бы и в ничтожнейших количествах, не учитываемых опытом, такие вещества, как железо и окись железа. Против такого допущения можно возражать; поэтому лучше дополнить вывод П. ф. простым соображением, по которому отсутствие тех или иных компонентов в тех или иных фазах влечет за собой одновременное выпадение одинакового числа как неизвестных (концентраций), так и ур-ий (равенств химических потенциалов), а поэтому их выпадение не влияет на решение системы ур-ий. Особый интерес представляет случай, когда две фазы в системе имеют одинаковый состав, например в случае диссоциации типа NH₄C1+: ϊ±ΝΗ₃ + ΗΟ, когда в газообразной фазе отношение ΝΗ₃ и НС1 то же, что и в твердой. Опыт показывает, что такая система ведет себя как о дно компонентная; однако стоит только ввести в систему избыток ΝΗ₃ или НС1, как система становится типично двухкомпонентной. Между тем в случае диссоциации СаС0₃+СаО + С0₂ мы имеем при всех условиях двухкомпонентную систему.

В первой системе мы имеем две фазы одинакового состава, во второй—три фазы, следовательно нет фаз одинакового состава. Если в системе две фазы имеют одинаковый состав, то к прежним условиям прибавляются новые—равенство концентраций компонентов в двух фазах:

C₁=С],

“ ^2»

вц-1 ” ^п-1»

то есть к числу ур-ий п(к — 1) прибавляется еще η - 1 ур-ий, число же неизвестных остается прежним, следовательно в этом случае п(к — 1) + п — 1=S к(п - 1) + 2,

или

3,

то есть всякая система, независимо от числа компонентов, ведет себя как одно компонентная, если в ней две фазы имеют одинаковый состав. Во втором случае с диссоциацией СаС0₃ мы имеем всегда двухкомпонентную систему, потому что смесь СаС0₃ и СаО рас-матриваем как две твердые фазы. Если бы мы сочли такую смесь за одну фазу, то получили бы полную аналогию со случаем диссоциации NHjCl. Но смесь двух веществ в твердом состоянии образует одну фазу только тогда, когда это твердый раствор. С термо-динамич. точки зрения определение твердого раствора базируется на П. ф., следовательно однозначно вопрос решен быть не может. Однако строение кристаллов подтверждает, что в данном случае мы имеем дело с двумя твердыми фазами, а не с одной (твердым раствором). П. ф., вводя строго определенные понятия компонента и степеней свободы, позволяет классифицировать бесчисленное многообразие равновесных систем в химии и дает возможность далекого и глубокого проникновения в область сложных физико-химич. свойств. Принято в основу классификации класть в первую очередь понятие компонента, во вторую—степени свободы.

Однокомпонентные системы состоят химически из одного индивидуального вещества (п=1). По данным опыта в однокомпонентных системах м. б. одна газовая, одна жидкая и несколько твердых фаз, но по правилу фаз одновременно в равновесии м. б. не больше трех фаз. Т. к. понятие о концентрации у однокомпонентных систем отпадает, то для определения их состояния достаточны лишь две независимые переменные: давление и Т°; следовательно для графич. изображения свойств однокомпонентных систем достаточно плоскости. Если на оси абсцисс станем откладывать Т°, а на оси ординат—давления, то система из трех фаз—инвариантная (фигура 1)—представится точкой А, т. к. такая система может существовать лишь при строго определенных значениях р и Т°. Напр. в случае воды три фазы—лед, жидкая вода и пар—находятся в равновесии при температуре + 0,0078° и 4,579мм давлениям Из числа трех данных фаз можно составить три системы по две фазы, например системы вода—пар, лед— «

пар и лед—вода. „ ,₆Двухфазная сис- s_/4тема моновариан- тна, а потому гра- %’²фически она в ди- $ ю аграмме предста- | ₈вляется кривой; ^ _gв нашем примере £ кривая АВ пока- ^ ^ίзывает изменения г давления с Т° в системе вода—пар, кривая С А—в системе лед—пар, DA—в системе лед—вода. Все эти три кривые пересекаются в точке А, которая называется поэтому тройной точкой. Известно, что в системе вода—пар давление пара зависит только от Т°, но не от объёма. Заметим, что это положение справедливо для всех моно вариантных систем независимо от числа компонентов. В случае однофазной системы (п= 1), например в случае воды, льда и пара по-

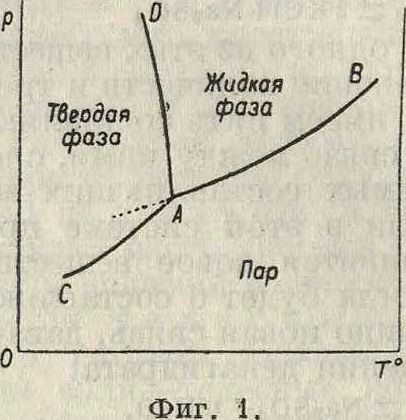
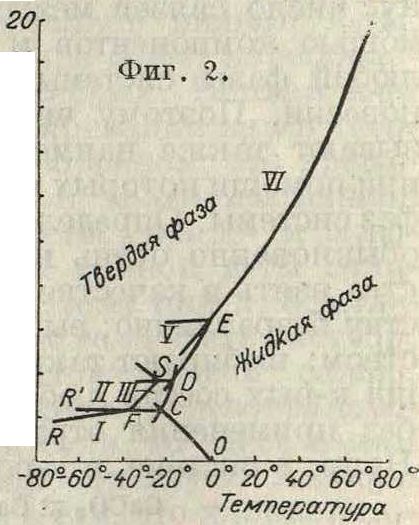
рознь, имеем две степени свободы, то есть можем изменять по произволу обе переменные р и Т° без того, чтобы изменилось число фаз. Графически таким дивариантным системам отвечают части плоскости между кривыми на фигуре 1. Это же явление отображается в уравнении состояния вещества: f(V, р, Т)=0. Изучение моно- и дивари-антных однокомпонентных систем составляет одну из основных задач физики (учения о газах, жидкостях, твердом веществе, агрегатных состояниях). Так как вещество может проявляться в виде нескольких твердых фаз (модификаций, см. Полиморфизм), то у каждого вещества м. б. несколько тройных точек; число тройных точек определяется опытом. Примером может служить вода с δ видами льда (фигура 2); координаты тройных точек здесь следующие.

Трой ная точка на фигура 2	Фазы	t°	Давление
О	Лед I—вода—пар	+0,0078	4,579 ММ
с	Лед I—вода—лед III	-22	2,115 килограмм{см²
D	Лед III—вода—лед Υ	-17	3,530 »
Е	Лед V—вода—лед VI	+ 0,16	6,380 »
F	Лед I—лед II—лед III	-34,7	2,170 »
S	Лед II—лед III—ледУ	-24,3	3,510 »

Лед IV, на существование которого указывал Тамман, повидимому не существует; вопрос о существовании разновидных фаз, например льдов Ши ИГ (смотрите Лед), остается совершенно открытым. Лед VI прослежен до давлений около 20 000 к г/см²· и до Г около 80° («горячий» лед).

Двух-компонентные системы характеризуются тремя независимыми переменными: р (или V), Т° и концентрацией одного из компонентов; если масса одного компонента m_lt второго т₂, то концентрация первого с= ^_т~, второго 1-е=-^;

графически свойства таких систем изображаются в пространстве. Максимальное число фаз, которые м. б. одновременно в равновесии, равно четырем. Инвариантная система (?г=2, к=4) существует при строго определенных значениях р, Т° и с то есть графически представляется точкой в пространстве. Эта точка является точкой пересечения четырех кривых моновариантных систем (п= 2, fc=3) и называется четверной точкой. Пример: система, состоящая из воды и соли; в инвариантном состоянии она может состоять из фаз раствора L, твердой соли S, льда Е и пара V. Из этих фаз можно составить четыре трехфазные системы: 1) L, S, V; 2) L, S, Е; 3) L, E, V; 4) S, E, V, с одной степенью свободы; в таких моновариантных системах давление не зависит от объёма (смотрите выше); им отвечают четыре кривые. Инвариантных систем (п=2, к=2) может быть шесть: V—L, V—S, V—E, L—S, L—Е,

S—Е. Число возможных систем значительно возрастает, если принять во внимание полиморфизм твердых фаз и то, что в двухкоыпо-нентных системах возможны две жидкие фазы (например вода и эфир). Двухкомпонентные системы изучены достаточно полно (смотрите Спр. ТЭ, тт. V, VI, VII, «Равновесие фаз»). Из их числа следует указать на системы, в к-рых протекает диссоциация (например CaC0₃i± ^СаО + С0₂, диссоциация кристаллогидратов), растворы индивидуальных веществ в различных растворителях, системы из двух несмешивающихся жидкостей, бинарные твердые растворы, бинарные сплавы, смеси двух летучих жидкостей (смотрите Перегонка), системы с динамич. и оптич. изомерой.

Трехкомпонентные системы характеризуются четырьмя независимыми переменными: р (или V), Т° и двумя концентрациями C₁ и с_а; полное их представление графически невозможно, так как для этого требуется четырехмерное пространство, следовательно мы можем давать только проекции в трехмерном пространстве, принимая одну из независимых переменных постоянной, Очевидно, что в инвариантной трехкомпонентной системе пять фаз; ей отвечает точка в четырехмерном пространстве, в ней пересекаются пять кривых моновариантных систем. Очевидно также, что число систем при и=3 весьма сильно возрастает и изучение их усложняется, а между тем практич. ценность трехкомпонентных систем огромна. Растворы двух солей в различных растворителях, двойные соли, тройные сплавы, смеси трех жидкостей (смотрите Перегонка) и т. д. являются трехкомпонентными системами. В тех случаях, когда два компонента резко отличаются по своим свойствам от третьего (например две соли и вода), можно применять обычные прямоугольные координаты, например откладывая на двух осях концентрации с и с 2, на третьей—Т° (р—постоянное). В других случаях, при изучении сплавов трех жидкостей и тому подобное., наиболее удобными являются треугольные координаты. О применении их см. Спр. ТЭ, т. VI и VII. В таких координатах мы имеем дело не с двумя концентрациями компонентов, а с ттн-мя концентрациями составляющих веществ; следовательно для изображения свойств системы при разных Т° (р—постоянно) или разных давлениях (Т°—постоянно) мы должны использовать треугольную призму.

Еще сложнее системы четырехкомпонентные и выше; они изучены слабо и только в виде отдельных конкретных примеров; между тем большое значение их станет ясным, если примем во внимание, что их изучение— непременная предпосылка к. рациональной разработке вопросов об отложениях морских солей (Стассфуртские, Соликамские и. другие отложения). Графич. методы для изображения свойств таких систем в известной степени условны; о них см. Спр. ТЭ, т. VII.

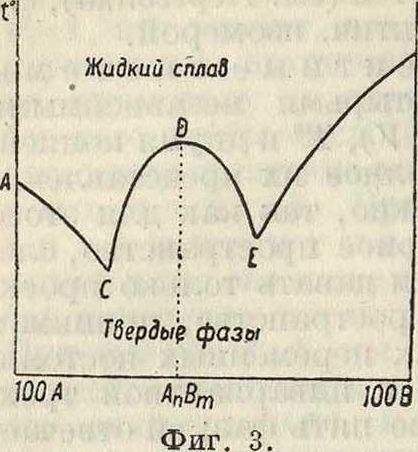
В основе применений П. ф. лежат два принципа: принцип непрерывности и принцип соответствия, или корреляции. Первый принцип утверждает, что свойства фазы изменяются непрерывно при непрерывном изменении переменных, определяющих ее состояние, то есть Т°, давления (или объёма) и концентраций компонентов; в случае гетерогенной системы ее свойства также изменяются непрерывно при непрерывном изменении указанных переменных до тех пор, пока число и характер фаз, входящих в состав системы, постоянны. Второй принцип относится к графич. представлению свойств системы и утверждает, что в случае диаграмм на плоскости каждой фазе соответствует особая ветвь диаграммы, и обратно — числом ветвей ее определяется число существующих фаз в равновесной системе: в случае пространственных диаграмм каждой фазе отвечает своя поверхность. На фигуре 3 показана обычная диаграмма плавкости смесей двух веществ А и Б; на оси абсцисс отло-⁸ жены %-ные содержания А и В в смеси, на оси ординат Г_я,_г или t°_ome. В данной системе вдоль кривых всегда имеется жидкая итвер-дая фаза; ветвь АС отвечает тем случаям, когда твердой фазой является А, ветвь BE—отвечает твердой фазе В, ветвь же CDE—твердой фазе—химич. соединению А_пВ_т (п и то— целые числа). С точки зрения принципа корреляции CDE—непрерывная кривая, D—ее максимум; абсцисса точки Ώ показывает состав соединения А_пВ_т. В точке Ώ можно провести только одну касательную к кривой CDE, и эта касательная параллельна оси состава.

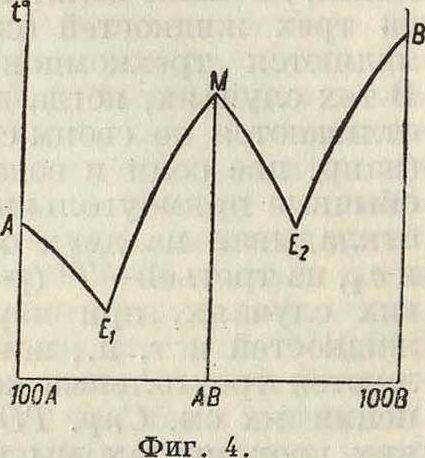
Можно подойти к вопросу с другой точки зрения. Допустим, что компонентами системы являются^. и соединение АВ (смотрите фигура

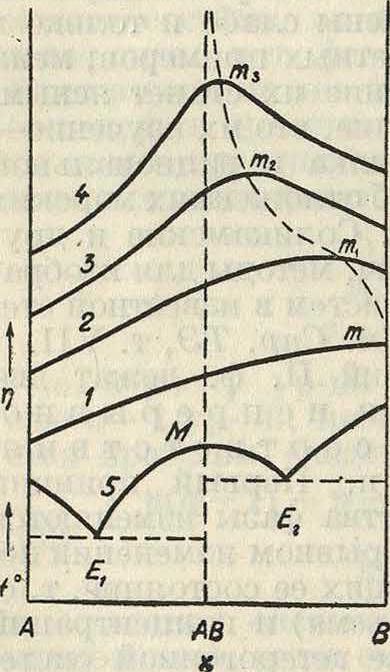
4); как прибавление АВ к А, так и прибавление А к АВ понижает t°,_U4 А, и соответственно АВ; мы получим две ветви: АЕ,—отвечающую твердой фазе А, и ME,— отвечающую твердой фазе АВ. Пусть теперь в качестве компонентов взяты МВ и В; в такой системе опять получим две ветви: ME.i—отвечающую соединению АВ, и Е_гВ—отвечающую твердому компоненту В. Очевидно, что в точке М должны брать начало две различные кривые ME, и МЕ₂, пересекающиеся в точке М. В ней можно провести две касательные. Между тем с опытной точки зрения в подавляющем большинстве случаев кривая плавкости соединения непрерывна и только проходит через максимум. Мы найдем о бъяснение, если станем изучать не только плавкость, но и другие свойства системы, например внутреннее трение, электропроводность и т. д. На фигуре 5 в верхней части даны схематически кривые внутреннего трения при различных t° жидкой фазы в системе, диаграмма плавкости к-рой, состоя щая из трех ветвей, показана в нижней части фигура Кривые внутреннего трения также показывают максимумы, но положения этих максимумов не совпадают с положением максимума плавкости Ж и различны при разных <°. Этот факт вполне объясняется соответствующим ходом с темп-рой диссоциации соединения АВ в жидкой фазе. Эта же причина объясняет, почему кривая плавкости соединения на фигуре 5 только проходит через максимум, оставаясь непрерывной: кривая из двух ветвей ME, и ME 2 может иметь место только в тех случаях, когда нет диссоциации соединения в жидкой фазе. Остается еще вопрос, почему абсцисса максимума плавкости Жотвечает составу соеди-"х ° нения, а абсциссы мак симумов внутреннего тре-Фш·. 6. ния—_нет_ Если бы соеди нение АВ не диссоциировало в жидкой фазе, то кривая плавкости и кривые внутреннего трения должны были бы иметь вид, показанный на фигуре 6; здесь все максимумы отвечали бы одной и той же абсциссе—составу соединения. Опыт показал, что такие системы действительно существуют. (Примеры таких систем были изучены академ.

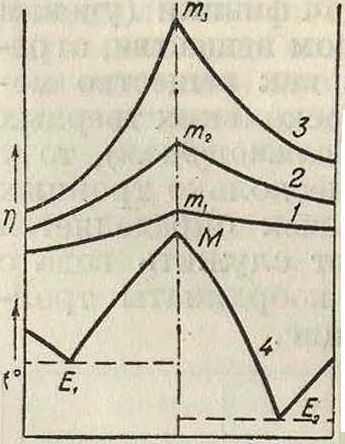
Н. С. Курнаковым и его учениками;к ним принадлежат системы из анилина, C₆H₅NH₂, и аллилового горчичного масла, CSN-C₃H₅, которые образуют аллил-фенилтиомочевину, CS · NH(C₃H₆) NH(C₆H,); далее, система: уксусный ангидрид и вода (соединение—уксусная кислота), серный ангидрид и вода (соединение—H₂S0₄). Таким образом опытом доказано существование таких систем, в которых одной и той же твердой фазе отвечаютдверазличныекривые.что противоречит принципу корреляции. Н. С. Курников и С. Жемчужный по казали, что это противоречие устраняется, если мы примем, что две ветви ME, и ME ₂ (фигура 6), пересекающиеся в точке Ж, являются не различными кривыми, а ветвями одной и той же аналитическ. кривой. Точка Ж,как и точки т„ т₂, т₃, ., с матема-тич. точки зрения суть особые син-гулярные точки непрерывных, кривых; они м. б. или узловыми точками (фигура 7, а), или точками возврата (фигура 7, б), или точками остановки—угловыми(фигура 7, e). С изменением параметров ур-ия кривой может произойти разрешение особой точки и переход от сингулярных кривых к обыкновенным.

В системах, о которых мы говорили выше, твердые фазы состоят из чистых веществ:

Фигура 5.

Фигура 7.

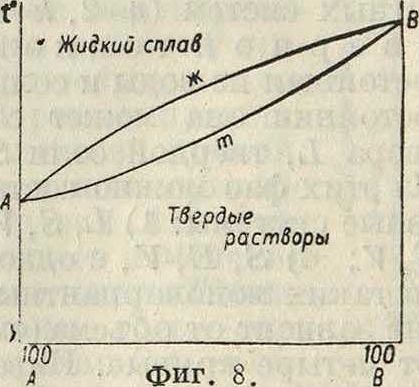
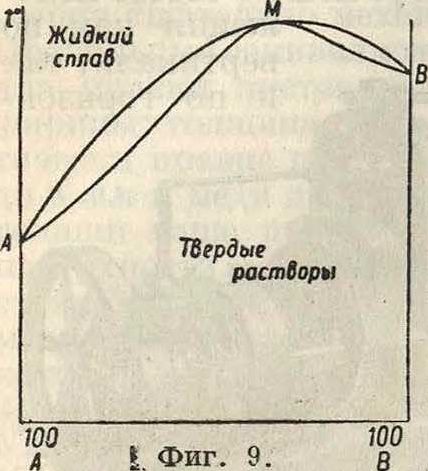
А или В или химии, соединения А_пВ_т. Но далеко нередки случаи, когда из жидкой фазы выделяются твердые растворы обоих компонентов или компонентов с химии, соединением. В данных случаях характерно то, что состав кристаллов твердого раствора,

выделяющихся из этого сплава, различен; мы получаем две кривые: кривую затвердевания жидкого сплава и кривую плавления твердого раствора. На фигуре 8 изображена диаграмма таких сплавов в простейшем случае, когда оба компонента смешиваются во всех отношениях как в жидком (ж), так и в твердом (т) состоянии. Фигура 9 отвечает случаю прохождения кривых через максимум М, в к-ром обе кривые соприкасаются, что указывает на одинаковый состав жидкого сплава и твердого раствора. Существование максимума указывает на образование соединения; если это соединение диссоциировано в обеих фазах, жидкой и твердой, то обе кривые непрерывны; в максимуме они соприкасаются и имеют одну общую касательную, параллельную оси состава; однако абсцисса точки максимума не отвечает составу соединения, она смещается под влиянием изменения условий (давления третьего вещества) опыта. Если соединение АВ не диссоциирует ни в жидкой ни в твердой фазе, то получим второй крайний случай,диаграмма которого показана на фигуре 10.Кривые обоего рода (ж — жидкости, т—твердых растворов) не проходят через максимуму пересекаются в точке М, сингулярной точке ветвей ж и ветвей т, обе ветви ж принадлежат различным кривым, так нее как и обе ветви т. Здесь абсцисса точки II отвечает определенному соединению АВ.

Средние случаи—очень многочисленные— имеют место, когда соединение АВ диссоциировано в жидкой фазе, но не в твердой. Тогда кривая жидкости оюж состоит из одной ветви, проходящей через максимум, а кривая твердых растворов тт состоит из двух ветвей, пересекающихся в точке максимума первой кривой (фигура 10, II). На фигуре 11 диаграмма а отвечает фигура 10, а диаграмма Ь— только-что описанному случаю. Т. к. состав соединения определяется составом твердой фазы, то точка М—точка пересечения ветвей жою—показывает состав соединения; а так как точка М одновременно является точкой максимума на кривой жидкости, то очевидно, что состав соединения можно определять также и по точке максимума плавления.

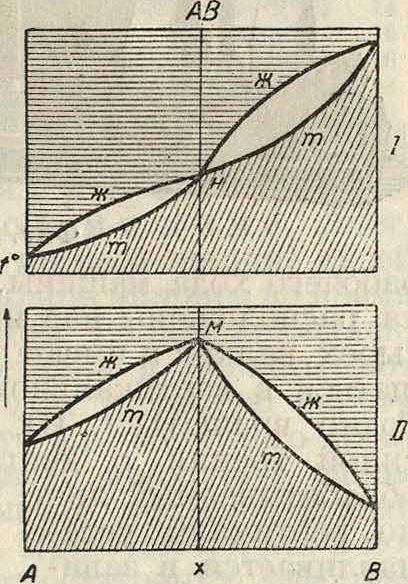
Фигура 10.

Часть плоскости между ветвями жж м. б. по величине весьма разнообразной, в пределе сойти на нет (диаграмма с фигура 11). Эта фигура дает ответ на вопрос, почему точка максимума плавкости бинарной системы (фигура 5) определяет состав соединения в том случае, когда соединение диссоциировано в жидкой фазе, не инвариантно и не отвечает постоянному составу соединения. Ответ ясен: потому что точка М на фигуре 5 совпадает с точкой пересечения ветвей твердых растворов, в пределе совпадающих друг с другом. Диаграмма d фигура 11 относится к случаю, когда соединение диссоциировано в обеих фазах; точка М—точка соприкосновения двух кривых—не определяет собою точного состава соединения, т. к. она смещается в зависимости от изменений внешних условий вместе со степенью диссоциации соединения. Изложенная здесь теория приводит нас к особому взгляду на химич. индивидуум, то есть на химически чистое вещество (соединение). Диаграмма Ь фигура 11 показывает, что опытные кривые дают нам указа-

а Ь с Й

МММ М

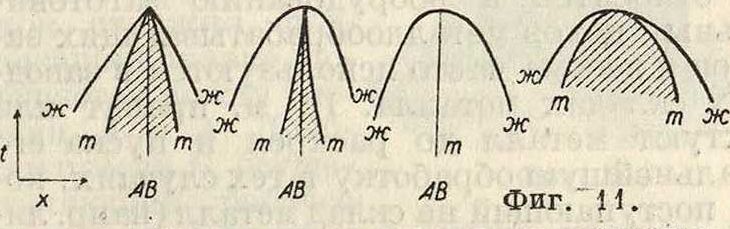
ния на определенное химич. соединение, но что в общем случае твердая фаза обладает переменной концентрацией, и только в предельных случаях (диаграмма с фигура 11) мы можем выделить чистое соединение в виде твердой фазы. Следует однако заметить, что общеизвестная трудность получения химически чистого вещества во многих случаях объясняется не только указанной здесь принципиальной причиной, но и чрезвычайной трудностью отделения твердой фазы от жидкой на практике.

Особенный интерес представляет случай, иллюстрируемый диаграммой d фигура 11. Здесь максимум кривых не соответствует соединению, подчиняющемуся закону кратных отношений Дальтона; сингулярные точки отсутствуют не только у кривых плавкости, но и у кривых различных свойств твердой фазы. Мы получаем твердую фазу переменного состава благодаря диссоциации соединения и в твердом состоянии. На такую фазу можно смотреть как на соединение в духе учения Бертолле (б е р т о л л и д ы, бертоллидный тип соединений по Н. С. Курникову); они повидимому весьма нередки среди металлич. сплавов и силикатов. Ряд примеров таких соединений найден Н. С. Курниковым и его сотрудниками. Т. о. теперь можно дать строгое определение понятия о химич. индивиде. «Химич. индивид, принадлежащий определенному химич. соединению, представляет фазу, которая обладает сингулярными или дальтоновскими точками на линиях ее свойств. Состав, отвечающий этим точкам, остается постоянным при изменении факторов равновесия системы» (Н. С. Курнаков). Заметим в заключение, что Н. С. Курнаков реально отметил аналогию между изменениями физич. состояний, выражаемых диаграммами «свойство—состав»,

систем и изменениями положения фигур, изучаемьши в особом отделе геометрии— т. н. геометрии положения, или топологии. Очевидно, что этот отдел математики может оказать существенную помощь химии при изучении равновесных систем.

Лит.: М л о д з e е в о к и и А. Б., Термодинамика и правило фаз, М., 1922; К у р н а к о в Н. С., Растворы и сплавы, в книге Менделеева Д., Основы химци, т. 2, стр. 503—556, 9 изд., М.—Л., 1928; К у р н а-к о в Н. С., Введение в физико-химич. анализ, 2 изд., Л., 1928; F i n d 1 е у A., The Phase Rule a. Its Applications, 5 ed., L., 1925 (русский перевод печатается); T a m m a η n G., Aggregatzustande, 2 Aufl., Lpz., 1923; Таммапп G.,Lehrbuchd. heterogenenGleicli-gewichte, Brschw., 1924; Roozeboom H. W„ В lituis u. SchreinemakersF. A., Die he-terogenen Gleichgewichte vom Standpunkte d. Phasen-lehre, Brschw., 1901—13; V a n-d e r-W aals-Kohn-s t a m in Ph., Lehrbuch d. Thermostatik, T. 1, Leipzig, 1927. А. Раковский.