 > Техника, страница 73 > Практическая астрономия
> Техника, страница 73 > Практическая астрономия
Практическая астрономия
Практическая астрономия имеет своей задачей определение видимых координат светил, географич. координат места наблюдения и местного времени, в соответствии с чем рассматривает соответствующие методы и изучает теорию инструментов. Определение прямых восхождений и склонений светил производится на постоянных обсерваториях (смотрите) меридианными кругами (смотрите) или пассажными инструментами (смотрите) и вертикальными кругами (смотрите). Определение времени, широты и долготы места наблюдения и азимута какого-нибудь объекта производятся для нужд повседневной жизни, геодезии, географии и мореплавания, пользуясь известными видимыми положениями звезд и других светил, данными в форме так называемым эфемерид через определенные промежутки времени. Соответствующих способов в зависимости от требуемой точности и применяемых инструментов имеется большое разнообразие.
Определение местного време-н и. Простейшим инструментом являются солнечные часы, дающие лишь грубые результаты. Более точными инструментами наблюдаются как Солнце, так и звезды. Последние наблюдают предпочтитель нее, так как наблюдения Солнца вследствие его большой яркости, сильного нагревания инструмента и отсутствия точно обозначенного центра представляют известные трудности и вообще производятся с меньшей точностью. При наблюдении звезд получается звездное время (смотрите), к-рое затем в случае надобности переводится в среднее солнечное или поясное время (смотрите). Наблюдения Солнца дают истинное солнечное время, к к-рому должен быть придано ур-ие времени для перевода в среднее время. Основных методов два: по прохождениям светил через меридиан или другой вертикал и по зенитнымрасстояниям. Первый способ в наиболее простом и точном виде осуществляется при помощи пассажного инструмента (смотрите). Из других вертикалов кроме меридиана имеет еще применение наблюдение в вертикале Полярной звезды. Однако этот способ требует довольно сложных вычислений и применяется редко. Определение времени по зенитным расстояниям производится вблизи первого вертикала либо путем точного измерения зенитного расстояния в известные моменты либо без измерения такового—путем наблюдения двух звезд (в частном случае и одной звезды два раза) на равных, но в общем точно не определяемых, зенитных расстояниях по разные стороны от меридиана. Для первого способа, называемого способом абсолютных з е н итных расстояний (или высот), необходим инструмент, имеющий точный вертикальный круг, то есть у ниве реальный инструмент или вертикальный круг; может употребляться и секстант (смотрите). Для второго способа точного круга не нужно, требуется лишь наличие чувствительного уровня для измерения небольших изменений в наклоне оптической оси инструмента, почему может употребляться и зенит-телескоп. Способ наблюдения двух звезд на равных зенитных расстояниях разработан Н. Я. Цингером, почему и называется способом Цингера, или соответствующих высот. Для подыскания звезд он требует особых таблиц, составленных Н. И. Щеткиным и в настоящее время расширяемых К. А. Цветковым. Этот способ имеет большое распространение в астро-номо-геодезич. работах в СССР. Наблюдение одной звезды на равных высотах требует -лишь очень простых вычислений, но два наблюдения бывают разделены большим промежутком времени в несколько часов, вследствие чего этот способ для звезд не употребляется. Лишь при наблюдении Солнца он представляет преимущества из-за простоты могущего применяться инструмента (солнечный треугольник или кольцо, разработанные проф. С. П. Глазенапом). Точность определения времени точными инструментами доходит до 0,01".
Определение широты места также м. б. произведено путем наблюдения прохождений светила пассажным инструментом или по зенитным расстояниям. В первом способе, разработанном В. Я. Струве, наблюдения производятся в первом вертикале на малых зенитных расстояниях. Способ этот требует хорошей установки инструмента, почему в экспедиционных уело-
| 100X16 | 120x22 | 160x22 |
| 1500 | 1800 | 2500 |
| 6 | 9 | 12 |
| 2—4,5 | 2-4,5 | 2—4,5 |
| 15 | 20 | 30 |
виях применяется редко. При определении широты по зенитным расстояниям наблюдения производятся в меридиане или около него. По способу измерения абсолютных зенитных расстояний (или высот) пользуются Полярной звездой и южными звездами, кульминирующими на зенитных расстояниях, близких к Полярной, но по другую сторону от зенита. Это делается для исключения влияния неточного знания рефракции (смотрите) и инструментальных ошибок. Очень точные результаты дает метод Таль-кот т а, основанный на измерении небольших разностей зенитных расстояний двух звезд, кульминирующих по разные стороны от зенита. Этот способ употребляется на международных станциях для исследования изменяемости широт, причем наблюдения производятся при помощи больших зенит-телескопов. Способ Талькотта начинает широко применяться и в геодезич. работах в СССР. Также весьма употребителен у нас способ, аналогичный способу Цингера, заключающийся в наблюдении двух звезд на равных зенитных расстояниях вблизи меридиана, разработанный М. В. Певцовым. Таблицы для нахождения звезд к нему составлены И. И. Селиверстовым. Точность определения широты в экспедиционных условиях достигает 0,1"; на постоянных обсерваториях еще выше.
Определение долготы сводится к сравнению местного времени в двух пунктах в один и тот же физич. момент. Раньше это делалось посредством перевозки хронометров. Затем передача и сравнение времени производились по телеграфу. В настоящее время этот вопрос получил полное решение благодаря радиотелеграфу. Ряд мощных радиостанций (Регби, Париж, Бордо, Лион, Науен, Детское Село, Москва-Октябрьская и др.) ежесуточно в определенные часы передают сигналы времени, даваемые часами одной из больших обсерваторий, причем поправка этих часов с точностью до 0,01" публикуется по ее определению из астрономических наблюдений. Прием этих сигналов на хронометр тоже производится с точностью не ниже 0,01". Если хронометр выверен по местному времени, то получается непосредственно долгота. Определение долготы можно еще производить по наблюдениям явлений, гриничское время которых м. б. вычислено; сюда относятся затмения спутников Юпитера, лунные и солнечные затмения, покрытия звезд Луною и определение координат Луны. Затмения Луны и спутников Юпитера происходят слишком постепенно, чтобы можно было заметить точно определенный момент; солнечные Hie затмения, пригодные для этой цели, бывают слишком редко. Покрытия звезд Луною наблюдаются чаще, но тоже связывают наблюдателя определенными моментами и требуют предварительного вычисления. Наблюдения Луны, а именно определение прохождения Луны через известный вертикал, измерение видимого углового расстояния Луны от звезд (при помощи секстанта), определение зенитного расстояния Луны могут производиться в любое время, если Луна видна над горизонтом. Однако обработка этих наблюдений довольно сложна, и получаемая долгота сильно зависит от неточно стей в координатах Луны, даваемых эфемеридами, почему и эти способы мало употребляются. Но было время, когда эти методы при длительных путешествиях были почти единственными.
Определение азимута производится гл. обр. по Полярной звезде при помощи универсального инструмента или теодолита. Этот метод требует знания точного местного времени. В виду важности определения азимута для съемочных работ, при которых редко бывает известно время с достаточной точностью, разработаны другие способы, свободные от этого требования. Сюда относятся способ наблюдения двух звезд в разных вертикалах, горизонтальный угол между которыми измеряется теодолитом, способ измерения зенитного расстояния звезды вблизи первого вертикала, наблюдение околополярных звезд во время наибольшей дигрессии и тому подобное. Точность определения азимута доходит до долей секунды дуги.
Лит.: Иванов А. А., Практическая астрономия, СПБ, 1914; Ц и н г е р Н. Я., Курс практич. астрономии, М., 1924; С а в и ч А., Приложение практич. астрономии к географическ. определению мест, СПБ, 1871; Матусевич Н., Мореходная астрономия, П., 1922; Campbell W., The Elements ot Practical Astronomy, L., 1922; Jordan W., Grundziige der astronomischen u. geographischen Ortsbestimmung, B., 1885; A 1 b r e c h t Tb., Formelnu.Hilfstafelnfiirgeo-grapbische Ortsbestimmung, Lpz., 1908; Admiralty Manual of Navigation, L., 1922; DuttonC., Navigation and Nautical Astronomy, Annapolis, 1926; Farwell R., Elements of Navigation, Seattle, .1927; С о n-stan P., Cours d’astronomie et de navigation des marines, T. 1—2, P., 1924. А. Михайлов.
Мореходная астрономия, отдел П. а., имеющий своей главной задачей определение места корабля в открытом море по наблюдениям небесных светил. Кроме этой основной задачи П. а. решает все имеющие значение для мореплавания вопросы, связанные с движением небесных светил: расчет времени восхода и захода светил, в частности Солнца и Луны, продолжительности сумерек, определение поправки компаса и т. д. Все свои решения П. а. основывает на известных в настоящее время, с достаточной для практич. целей точностью, законах движения небесных светил, на той связи, которая во всякий момент существует между положением светила на небе и местом наблюдателя на земле и наконец на произведенных с корабля наблюдениях над светилами.
Взяв центр небесной сферы (смотрите Сферическая астрономия) в центре земли (фигура) и условившись отсчитывать часовые углы светил от какого-нибудь определенного меридиана, можно сказать, что астроно-мич. экваториальные координаты самого светила А (его склонение и часовой угол) и географич. координаты проекции этого светила а на земной поверхности в градусной мере соответственно равны друг другу. Экваториальные координаты светила А: склонение β, равное дуге В А, и гриничский часовой угол t=EPnB; географич. координаты проекции светила на земной поверхности: широта ее, равная дуге bа, и долгота от Гринича ерb. В градусной мере широта проекции светила равна склонению самого светила и одного с ним наименования, то есть Ьα= В А или φ=δ·, долгота проекции, считаемая от Гринича, равна гриничскому часовому углу светила, то есть ерb=ЕРпВ или l=t. Т. о. склонение и гриничский часовой угол светила дают нам широту и долготу проекции светила на поверхности земли, то есть той точки, где светило приходится прямо над головой наблюдателя, или в зените наблюдателя. Измерив секстантом высоту светила h, наблюдатель рассчитает зенитное расстояние светила У 90 b. к-рое ему
ft
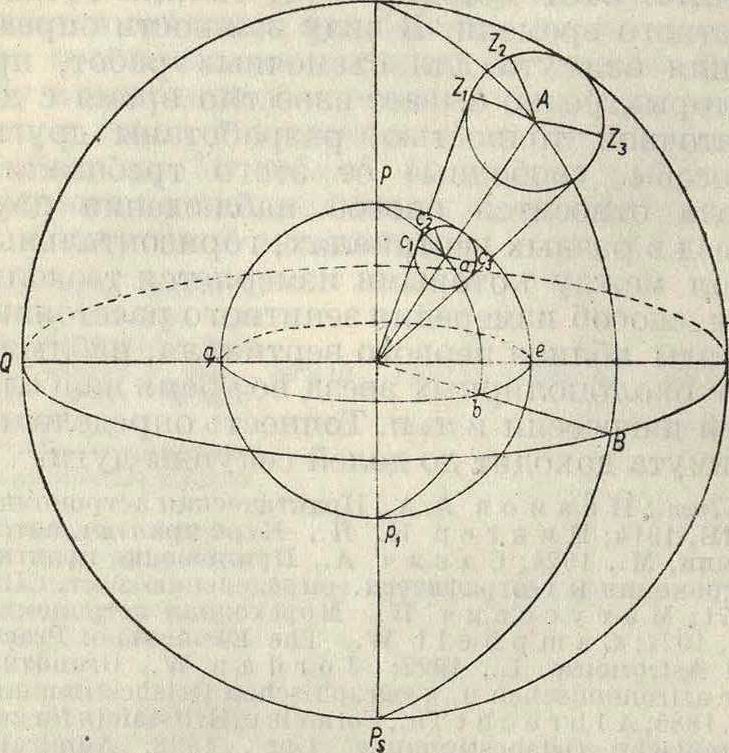
покажет, что между зенитом наблюдателя и местом светила на небе столько то градусов и долей градуса. Значит, если место светила А на небесной сфере известно, то, очертив из этой точки круг радиусом, равным зенитному расстоянию Z светила, мы получим на сфере малый круг У±У2У3, в одной из точек которого непременно должен находиться зенит наблюдателя. Соединяя все точки этого малого круга УгУгУг небесной сферы с центром земли, получим на поверхности последней тоже малый круг с^Сз, все точки которого будут отстоять от проекции светила а на расстоянии асх, равном измеренному зенитному расстоянию светила; значит, в одной из точек этого круга непременно должен находиться корабль. Этот малый круг называется кругом равной высоты, т. к. для всех наблюдателей, расположенных в любой его точке с^Сд, ., светило представляется на одной и той же высоте. Так. обр. измерение высоты светила, при известном его склонении и гриничском часовом угле, дает круг равной высоты, или линию положения корабля. Следовательно для получения места корабля нужно пронаблюдать два светила, начертить на глобусе два круга равных высот и одна из точек пересечения этих кругов определит собой искомое место. В большинстве случаев точки пересечения будут далеко отстоять одна от другой, так что с ч и с л е-н и е (смотрите Навигация) пути корабля, дающее уже приближенно его место, поможет разобраться, в какой из этих двух точек находится корабль. Вышеизложенный способ определения места корабля пересечением кругов равных высот и есть т. н. способ С о м н е р а. открытый случайно во время плавания америк. капитаном П. Сомнером в 1837 г.; с того времени и до. наших дней способ этот остается наилучшим. Т. к. мореплавателя интересует именно точка пересечения кругов равных высот, то на прак тике на карте чертят только небольшие отрезки кругов равных высот, принимаемые за прямые линии и называемые с о м н е р о-в ы м и линиями. Их пересечением графически определяется место корабля на карте. Так. обр. вся работа по определению места корабля разбивается на следующие части: 1) астрономические наблюдения, 2) вычисления необходимых величин для проведения сомнеровых линий, 3) прокладка на морской карте сомнеровых линий, 4) снятие с карты широты и долготы точки пересечения сомнеровых линий, т. н. обсервиро-ванного места корабля.
Астрономия, наблюдения состоят в измерении секстантом высоты светила над видимым горизонтом и в определении показания хронометра (смотрите) в этот момент. Взятая высота исправляется поправками на рефракцию, понижение’ горизонта и, при наблюдениях солнца, на п о л у д и а-м е т р светила и его параллакс (смотрите). Для расчета гриничского часового угла светила, по моменту на хронометре необходимо знать поправку хронометра и его ход. Далее нужно знать склонение светила и уравнение времени при наблюдениях солнца или звездное время (смотрите) в средний гриничский полдень данного дня, при звездных наблюдениях. Все эти данные выбираются из специального морского астрономия, ежегодника, издаваемого заблаговременно на предстоящий год. Затем посредством м о р е-ходных таблиц вычисляют высоту h0 светила и его азимут А, которые наблюденное светило должно было бы иметь, если бы корабль в момент наблюдения находился в своем счислимом месте. Эти вычисления производятся посредством 4-значных лога-рифмич. таблиц по следующим формулам:
sin h0=sin ψ sin δ + cos φ cos δ cos t и
sin A=cos (5 sin t esc h0,
где φ — счислимая широта судна, а δ и t— склонение и местный часовой угол светила, рассчитанный по гриничскому часовому углу светила с учетом счислимой долготы судна. Вычисленную высоту ha сравнивают с истинной высотой светила h, измеренной секстантом и исправленной всеми поправками и, в зависимости от знака разности · h—h0, откладывают эту разность высот от счислимого места судна на карте по направлению вычисленного азимута, то есть по направлению к светилу (если h > h0) или в обратном направлении (если h < h0). Через полученную точку проводят прямую, перпендикулярную к линии азимута, и получают сомнерову линию. Сделав то же построение и для второго светила, в пересечении сомнеровых линий получают место корабля. При наблюдениях солнца приходится наблюдения производить два раза, причем промежуток времени между наблюдениями должен быть достаточен (2—3 часа), чтобы азимут солнца успел измениться не менее, чем на 30°. Если корабль за время между наблюдениями перемещался, то про-плытое. за это время расстояние вмещают между сомнеровыми линиями. Точность полученного места зависит от точности наблюдений и счисления пути корабля за время между наблюдениями и в лучшем случае не превосходит 3—4, то есть 3—4 морских миль, что для океанского плавания вполне достаточно.
Для получения высоты и азимута без помощи логарифмов существует много разного рода таблиц, например таблица Фуса, из которых по <р, д и t выбирается h0 и А. Недостатком этих таблиц является необходимость интерполяции по нескольким аргументам, чтобы получить h0 с точностью до 1 дуги. В последнее время появились приборы, напоминающие счетные машины, посредством которых, по предварительной установке их на у, δ и t, можно сразу, поворотом ручки прибора, получить h0 и А без всяких вычислений. Однако подобные вычислительные машины пока еще мало распространены.
Лит.: Матусевич Η. Н., Мореходная астрономия, П., 1922. Подробный курс практич. астрономии с исследованием точности и ошибок получаемых результатов; Шульгин Г. И., Мореходная астрономия, П., 1924 (полный курс Военно-морского училища); Сакеллари Н. А., Сущность кораблевождения, 2 изд., гл. 3, Л., 1926 (порное изложение основ практической астрономии); Бес-пят о в Μ. М., Задачник по мореходной астрономии, Л., 1930; Иванов А. А., Практическая астрономия, Берлин, 1923; его же, Основной курс теоретической астрономии, Берлин, 1923. Н. Сакеллари.