> Техника, страница 73 > Практическая математика

Практическая математика

Практическая математика, комплекс методов и приемов производства вычислений в приложениях (т. н. технических вычислений). Данные, над к-рыми производятся технич. вычисления, только приближенные вследствие неизбежной неточности наблюдений и измерений. При вычислениях можно довольствоваться приближенными результатами при условии, что погрешности в них не будут превосходить известного предела, к-рый в каждой задаче устанавливается из практики. Практика выработала нек-рые основы техники вычислений, например четкое изображение ма-тематич. знаков и цифр, пользование клетчатой бумагой, выписывание на отдельных карточках часто повторяющихся цифр, употребление «схем», предварительный (приблизительный) расчет, особые поверки, повторительное вычисление, определение искомой величины вычислением и графически.

При приближенных вычислениях пользуются таблицами логарифмов (например пятизначными таблицами Гаусса, Глазенапа, Пржевальского). При вычислениях меньшей точности логарифмические таблицы м. б. заменены логарифмической линейкой (смотрите); здесь относительная точность в среднем до ¹/₃₀₀, в линейках большого размера она доходит до ¹1 goo, следовательно превышает точность четырехзначных логарифмов. Когда точность, даваемая логарифмической линейкой или таблицами логарифмов, недостаточна, умножение и деление необходимо выполнять непосредственно, пользуясь или счетною машиной (смотрите) или таблицами произведений, дающими готовые результаты перемножения чисел с несколькими знаками. Кроме произведений таблицы могут содержать квадраты, кубы, корни квадратные и кубические, длины окружностей и площади кругов данного радиуса, величины обратные данным ч. Так, таблицы Крелля дают произведения всех трехзначных чисел; таблицы О’Рурка дают произведения трехзначных чисел на двухзначные; таблицы Асатиани—произведения трехзначных чисел на двухзначные и четырехзначных на однозначные и др.

При пользовании таблицами Крелля множители разбивают на группы по три цифры и находят соответствующие произведения, причем к каждому произведению приписывают столько нулей, сколько их было в обоих соответствующих сомножителях вместе.

Пример: 145 205 х 317 402=46 038 357 410.

145X317=45 965 000 000 145X402= 58 290 000

205x317= 64 985 000

205 x 402=82 410

46 088 357 410

При делении делитель разбивают на группы по три цифры, в делимом отделяют 5 или 6 первых цифр в зависимости от того, будет ли первая цифра делимого больше или меньше первой цифры делителя; остальные цифры делимого разбивают на группы по 3 цифры. Первые три знака частного представляют найденное в таблицах.число, произведение которого на отделенную часть делителя всего ближе подходит к отделенной части делимого. Вычтя из делимого найденные в таблице произведения трех знаков частного на группы делителя, сносят к остатку следующую группу делимого, делят первую группу остатка на первую группу делителя и т. д. В случае таблиц О ’Рурка в частном ищут не три цифры, а две. В таблицах четвертей квадратов умножение производится на основании ф-лы:

4 4

Существуют таблицы и для приближенного умножения. Таковы трехзнаиные таблицы Нумерова, дающие точность логарифмической линейки среднего размера.

Номограммы. Кроме числовых таблиц применяются (особенно .для функций с числом переменных более двух) скалярные таблицы, или номограммы. См. Номография.

Графическое решение. Сущность графич. методов решения состоит в том, что входящие в вопрос величины представляют в виде отрезков, взятых в известном масштабе, или углов или ф-ий их. В отличие от номограмм графич. решение выполняют отдельно для каждого числового примера. Точность графич. приемов повышают, применяя одновременно и вычисление. В нек-рых случаях графический прием дает единственное возможное решение.

С л о ж о н и е н вычитание. Алгебраическое сложение величин, представленных в определенномжасштеа-бе (смотрите) в виде отрезков, выполняют вдоль прямой линии при помощи линейки или циркуля.

Для определения суммы вида f(z)=<р(х)+ч>{у) можно применять прибор типа раздвижной счетной линейки.

Умножение и деление. аb

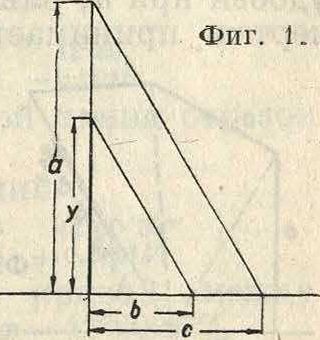
Для оп-Ь и ределения у из выражения?=где а с—данные величины, можно применить наир, прием, указанный на фиш 1. Выражение вида:

У =

= ± Vi ± У г ± Уг ±

61

Ьо Ьз,

си - ± сц— ±

с-2 ⁰С₃

определяют многократным применением того же приема; так, на фигуре 2 дано у=у_г+ +у₂—у₃. При применении логарифмическ. масштаба (вместо равномерного) приходят к при

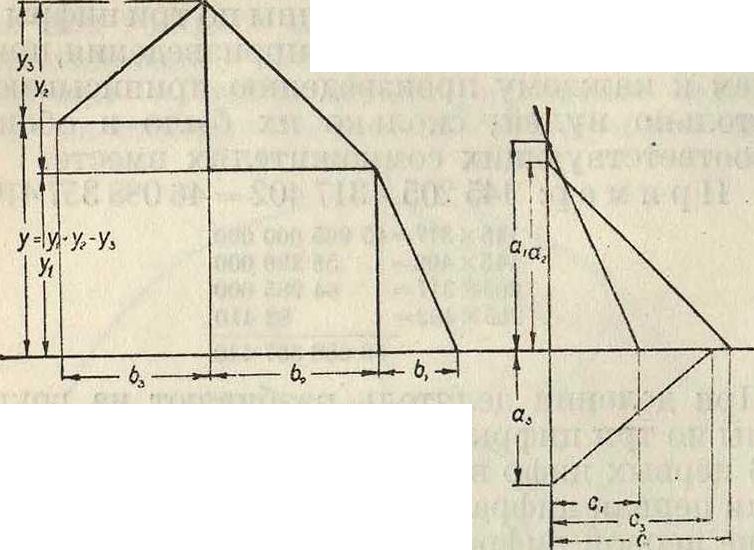
ему, применяемому при пользовании логарифмич. линейкой.

Возвышение в степень и извлечение _{фиг 2}.

корня. Определение а" для целых значений и м. б. произведено следующим способом. На двух взаимно перпендикулярных осях XX И УУ откладывают отрезки; О А=1 и ОС=а на оси XX (фигура 3)

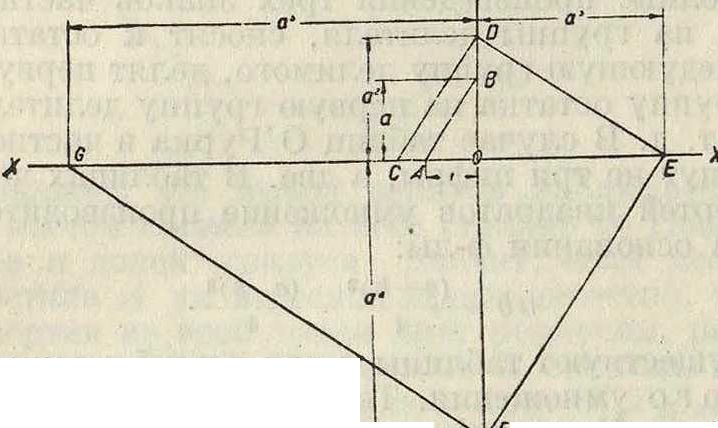
и О В=а на оси УУ; соединяют прямою

ТОЧКИ А И В И Прово- Фигура 3.

дят CD II АВ. Из по- *

лученных треугольников очевидна зависимость: OD : ОВ=ОС : ОА, или ОВ=а². Далее, проведя DE×CD, из тр-ков COD и EOD получают: ОЕ : ΟΙ)= 0Ώ : СО, откуда

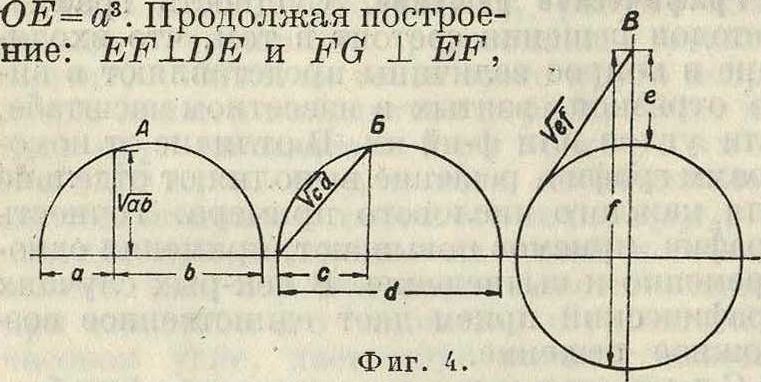
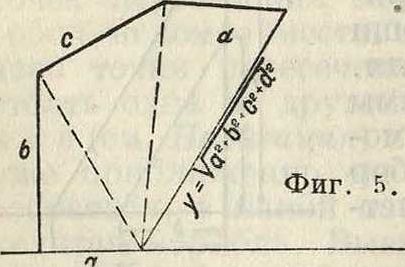
находят OF=a^l, OG=a⁶ и т. д. Способ этот удобен при а, близком к единице; при а >1 чертеж принимает большие размеры; при а < 1 точность определения мала. Извлечение квадратного корня производится при помощи круга (фигура 4). Извлечение корней высших степеней, за исключением степеней 2^ге, возможно только при помощи кривых линий, например при помощи логарифмич. спирали. Выражение вида у=у а”- + 6² + с² +.

определяется многократным применением пифагоровой теоремы (фигура 5).

Диференци рование. Чтобы определить значение производной у от ф-ии y=f(x) для данного значения х=а, проводят из точки К прямую, параллельную касательной к кривой при х =а (фигура 6). Масштабы для х и у м. б. различны, но 0К=1

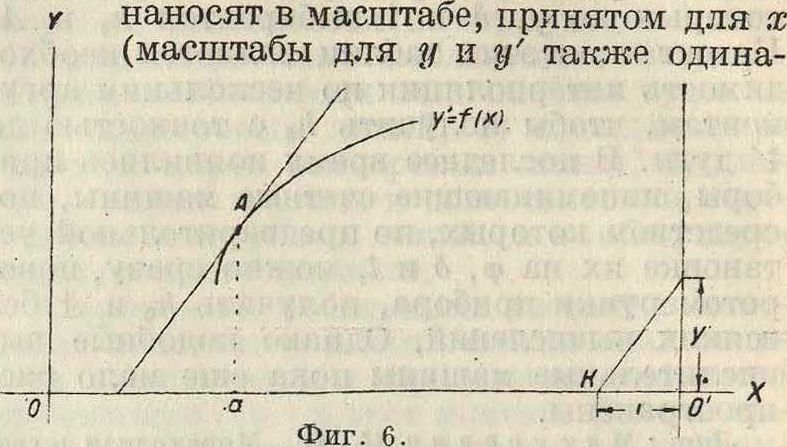
ковы). Точность -значения у мояшо повысить, определяя возможно точнее положение касательной, для чего вычисляют по точкам весьма малый отрезок кривой и строят его в увеличенном масштабе. Найденные указанным выше способом значения у для достаточного количества значений х наносят как ординаты и полученные т. о. точки А, В, С,. (фигура 7) соединяют непрерывной ли

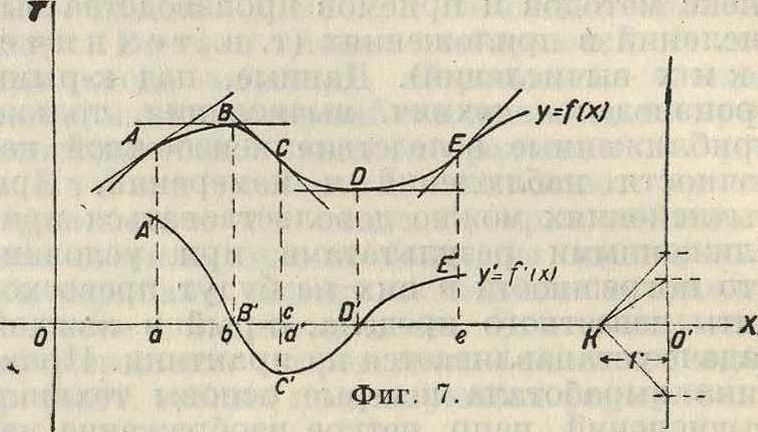
нией у=/(ж), которая является д и ф e р е н-циальной кривой (кривой угловых коэфициентов) по отношению к данной кривой у=/(ж). Для вычерчивания диференциальной кривой определяют ее некоторые точки, наир, точки пересечения ее с осью ОХ и высшие и низшие точки, соответствующие высшим и низшим точкам и точкам перегиба данной кривой.

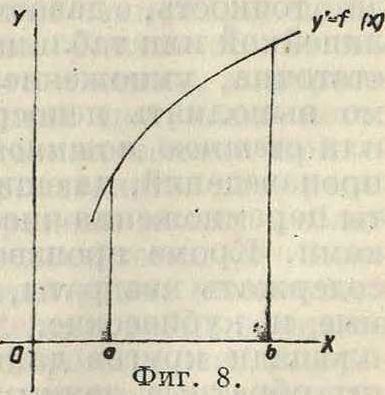
Интегрирование. Как известно, определенный интеграл

У=JГ(х) dx

а выражается площадью Р, ограниченной осью ОХ, кривой у=/(ж) и двумя прямыми ж=а и ж= 1> (фигура 8).

Определение площади Р производится обыкновенно или по формуле трапеций или по формуле Симпсона, а также по формулам Чебышева или Гаусса (смотрите Вычисления приближенные). Помимо указанных интерполяционных методов ^г применяется вычисление определенных интегралов при помощи рядов (смотрите). Если кривая у=/(ж) имеет общие точки с осью ОХ, то части площади Р, лежащие под осью ОХ,

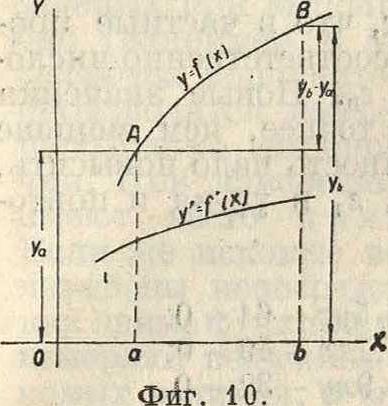
считаются отрицательными (фигура 9). Если соотношение между переменными задается не аналитически, а графически, то есть посредством некоторой кривой (барограф, индикатор паровой машины и другие самозаписывающие приборы), то аналитич. метод уже неприложим, если нельзя получить ур-ия кривой. Значение определенного интеграла в этом случае м. б. найдено с помощью интегральной кривой

Фигура 9

y=f(x), соответствующей (фигура 10) кривой y=f(x). Точкам последней для ж=а и х=Ь соответствуют точки А и В на интегральной кривой; разность ординат у_ъ-у_а и представляет численно значение у интеграла, причем у—положительно, если В лежит выше А, и отрицательно в противоположном случае. Т. к. кривая у=/(ж) является диференциальной кривой по отношению к кривой y=f(ж), то первой кривой соответствует бесконечное множество подобных между собою интегральных кривых. Обыкновенно вычерчивают интегральную кривую, проходящую через начало координат.Площадь Р_а(фигура 11) Очевидно м. б. выражена так:

а

Р_а=fydx= [у]_х=а^у_а·

о

Т. о. для одной и той же абсциссы ш= а число, выражающее длину ординаты интегральной кривой y=f(x), равно числу, выражающему площадь, заключенную между начальной кривой, осями и ординатой, соответствующей этой абсциссе. Определив площади Р_а для достаточного количества значений а, наносят соответствующие точки А и, соединив их непрерывной прямой, получают интегральную кривую y=f( ж), принадлежащую кривой y=f(ж).

на касательной в А. При проведении касательной масштаб для ординат как диференциальной, так и интегральной кривой один и тот же. Для кривой у=/(ж), пересекающей ось ОХ в любой точке М,_: вычерчивают такую интегральную кривую, которая касается оси ОХ в точке М (принимая, что нулевая точка координатной системы перенесена в М). См. также Графическое интегрирование. О приборах для приближенного интегрирования и гармонии. анализаторах см. Интегрирующие приборы и Гармонический анализ.

Определение действительных корней алгебраического или трансцендентного уравнения. Если для ур-ия Дж)=0 принять f(x)=y, то оно определит нек-рую кривую, к-рую можно нанести по точкам, причем искомыми корнями ур-ия

явятся абсциссы точек пересечения кривой с осью ж-ов. Точность полученных значений корней, завися от масштаба и качества выполнения чертежа, м. б. повышена, если отрезок кривой, примыкающий к соответственной точке пересечения кривой с осью абсцисс, наносить по частям в последовательно увеличивающемся масштабе; причем чем меньше будет наносимый отрезок, тем более этот отрезок будет приближаться к прямой линии.

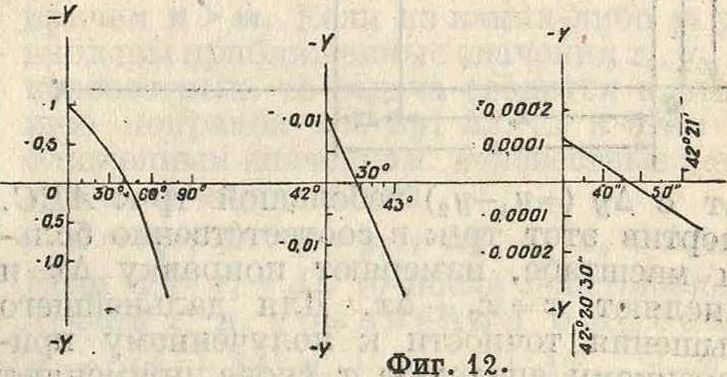
Пример. Определить с точностью до 1" значение острого угла, удовлетворяющее уравнению cos ж — ж=0. Для построения кривой у=cos ж — ж (фигура 12) по точкам имеем пары значений для ж и у, приведенные в следующей таблице.

Элементы	0°	10°	20°	30°	40°	50°	60°	70°	80°	90°
COS X.	1	0,98	0,94	0,87	0,77	0,64	0,50	0,34	0,17	0
X..	0	0,17	0,35	0,52	0,70	0,87	1,05	1,22	1,40	1,57
У..	1	0,81	0,59	0,35	0,07	-0,23	-0,55	-0,88	-1,23	-1,57

При нанесении интегральной кривой вы-

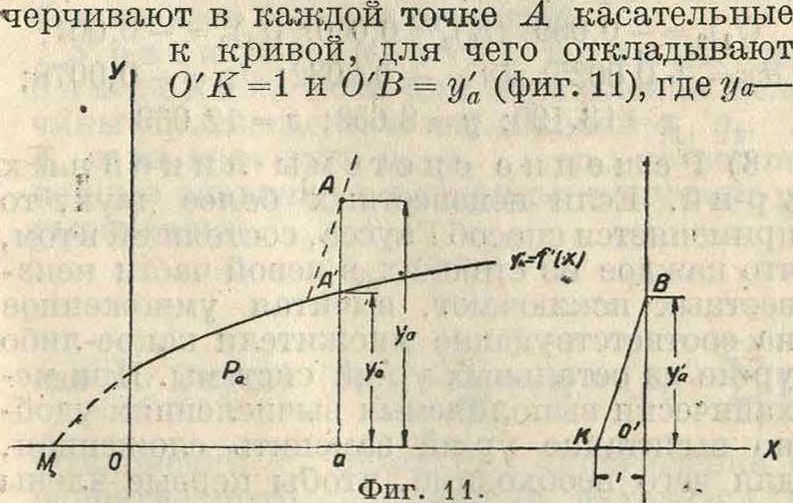
ордината точки А диференциальной кривой для ж=а; прямая КВ будет параллель-

Полученная кривая дает ж=42°. Берем пары значений:

. X. 42° 43° 42°30

у. + 0,0101 -0,0191 -0,0045

Нанесенный в виде прямой линии отрезок кривой дает ж=42°20.

Наконец для пар значений

Ж. 42° 20 42°21 42°2030"

у. +0,000383 - 0,000103 + 0,000140

прямолинейный отрезок кривой между 42°2030" и 42°2100" дает ж=42°2047".

Определение корней системы двух алгебраических или трансцендентных уравнений с двумя неизвестными: у=/(ж) и у=<р( ж). Найдя ряд точек, наносят кривые, определяемые этими ур-иями (фигура 13). Координаты точки пересечения А обеих кривых являют-

18

Т. Э. m. XVII.

ся приближенными значениями х и у. Для i нахождения более точных значений корней ] измеряют приближенное значение х₀ и, под- I ставив его в данные ур-ия, получают: у_х=|=/(ж₀) и у₂=<р(х,)· Проведенные в точке пе-ресечения обеих кривых касательные обра- I

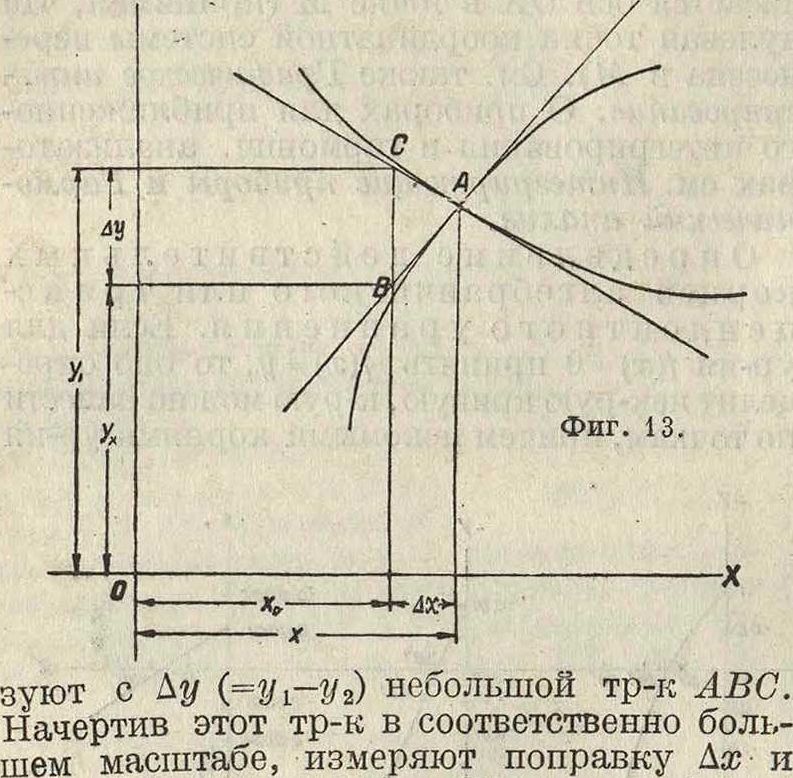
вычисляют х=ж₀ + Аж. Для дальнейшего повышения точности к полученному приближенному значению ж снова применяют тот же прием. В связи с увеличением масштаба треугольника соответственно увеличиваются масштабы абсцисс и ординат главной фигуры.

Интерполяция. Задача интерполяции—· см. Вычисления приближенные. Во многих случаях, если не требуется большой точности, задача эта м. б. решена графически: парные значения (х_х, у χ), (ж₂₎ у₂), ., (х_п, у_п) рассматривают как прямоугольные координаты точек и, нанеся на чертеж, соединяют их некоторой кривой, при помощи которой находят значение ф-ии у=Уг для ж=ж_г·. При решении задачи вычислением обычно применяют или формулу Ньютона (смотрите Вычисления приближенные) или формулу Лагранжа. Последняя имеет вид:

(ж-ж2) (х-хз) ··	,(х-хя)
(Χχ-Χ2) (Жх-Жз) ·	(*Х —ЖИ) -

(я-ЗСх) (х-х₃) (Х-Хп).

⁺ (я₂-Хх) (Ж₂-ЖЬ). (Хц-Хп)

, (Ж-ЗС1) (x-x-l). (Х-Х„-_Х)

(Ж/f Жх) (Ж_И-Ж₂). (Х_п~Х„—χ) ^

Решение уравнений. Обычно при решении численных ур-ий известны приближенные значения корней, и необходимо найти их более точные значения. Но если приближенные значения корней неизвестны, их нужно предварительно найти. При вычислении действительных корней при этом находят их границы, то есть числа, между к-рыми содержатся все корни ур-ия. В случае системы совместных ур-ий приближенные действительные значения находят графически, строя кривые, выражаемые например ур-иями /(ж, у)=0 и <р(х, у)=0, и отмечая координаты точек их пересечения. Если же нужно найти не только действительные, но и мнимые корни или если построение соответствующих кривых слишком сложно, то необходимо исключить из обоих ур-ий одно неизвестное и решать полученное ур-ие с Одним неизвестным.

1) Вычисление приближенных корней алгебраического или трансцендентного у p-и я. Наиболее-употребительны способы: а) правила ложного положения (Regula falsi) и б) способ Ньютона (смотрите Вычисления приближенные). См. также Греффе способ.

2) Вычисление приближен и ы х корней системы алгебраических и л и трансцендентных уравне-н и й. Даны ур-ия: f_x(x, у, z)=0, /₂(ж, у. z)== 0, /з(ж, у, z)=0. Если х₀, у₀, z₀—приближенные значения неизвестных, то можно найти поправки к ним dx, dy и dz из ур-ий, которые по правилу Тейлора по опущении, членов с dx², dx³ и т. д. получатся в виде:.

(Wo^dX + Шо^аУ + (§)/* +=⁰

+Ш/^у+Оо^⁺⁼⁰ (Έ)„^άχ+(t)o^ду+(а“+(«·=°

Индекс «0» показывает, что в частные производные подставлены соответственно числовые значения ж₀, у₀, z₀. Новые значения ж₁₍ у_х, z_x будут тем точнее, чем меньше· dx, dy, dz; если их точность надо повысить, то подставляют ж₁₅ у_х, z_x в ур-ия и повторяют вычисление.

Пример.

/х=У² + z² - 1,5yz~ 64= 0;

/₂=z² + х² — 1 ,ΐζχ - 49=0;

/₃=х² + у² — 1,9жу — 32=0. Соответствующие диференциальные ур-ия· суть:

(2у₀- 1,5г„) dy + (2ζ₀-Ι,δу₀) dz + (/₁)₀=Ό| (2ж„- 1,7г₀) dx + (2z₀ - 1.?ж₀) dz + (f_t)₀=0 ; · (2ж₀ - 1,9y₀) dx + (2y₀ - 1,9ж„) dy + (/₃)„=0 J После подстановки найденных приближенных значений: ж₀=13, у₀= 9, г₀= !2, получаем (/₁)о=-1; (/₂)о=- 1,2; (/з)₀=— 43 т следовательно:

0,0dy + lO.odz — 1 =0 )

5,6dx + l,9dz — 1.2=0 ;> 8.9dx — 6,7dy- 4,3=0 J

откуда dx=+ 0,182; dy=- 0,400; dz== + 0,095. T. о. новые значения таковы: ж_г= 13,182; у_х= 8,600; z_x= 12,095. Подставив· полученные значения в первоначальные ж диференциальные ур-ия, получаем:

(/1)1= +0,223; (/_а)_х= + 0,013; f₃=+ 0,331;. dx= + 0,0051: dy=+ 0,0485; dz=— 0.0239;

ж₂= 13,187; 2/2=8,619; г₂=12,071. Новая операция дает:

(/х)₂=-0,089; (/₂)₂= 0,000: (/₃)₂=- 0,001; dx=+ 0,0025; dy=+ 0,0032; dz=— 0,0078; ж=13,190; у=8,652; г=12,063. *

3) Решение систем ы линейных ур-ий. Если неизвестных более двух, то применяется способ Гаусса, состоящий втом, что каждое из стоящих в левой части неизвестных исключают, вычитая умноженное на соответствующие множители какое-либо ур-ие из остальных ур-ий системы. При механически выполняемых вычислениях удобно вычитание ур-ий заменить сложением, для чего необходимо, чтобы первые члены каждой пары ур-ий· имели разные знаки. Вычисление коэфициентов вновь образуемых ур-ий молено производить при помощи вычислительной линейки. Если требуется ! большая точность, то, пользуясь счетной I машиной, логарифмами или счетной линей- ! кой, получают приближенные значения ж₀, i у₀, z₀, ., поправки к которым Ах, Ay, Az,. | м. б. далее определены опять при помощи : счетной линейки. Если в данные ур-ия а_хх + b_ху -f c_xz -f 1_Х=0 1 а₂х + Ь₂у + c₂z + 1₂=О а₃х + Ь₃у + c₃z + l_s=О

ввести подстановки х=х_а + Ах, у=у₀ + Ау, z=2₀ + Az, то ур-ия примут вид:

а_хАх + Ь_хАу + c_xAz + А1_Х=О 1 а₂ Ах + Ь₂Ау + c₂Az + А1₂=0 > а₃Ах + Ь₃Ау + c₃Az + А1₃=О J где

А1_Х=а_ххо -F.bij/o + c_xz о + 1_Х

А1₂=а₂х₀ + Ь₂уо + С2^го + h i

А1₃=а₃х₀ + b₃у₀ + c₃z₀ + l_s )

Способ наименьших квадратов. В виду возможных при выполнении наблюдений ошибок (например в астрономии, в геодезии) делаются дополнительные наблюдения, то есть производится наблюдений больше, чем это необходимо для определения искомых величин. При измерении независимых величин имеют место прямые наблюдения. Если же искомые величины не могут быть измерены непосредственно и представлены как явные функции измеряемых величин, то измеряют величины ф-ий, зависящих от искомых величин, и получают систему ур-ий, в которые искомые величины входят как неизвестные (вспомогательны? наблюдения). Вследствие ошибок, содержащихся в ур-иях, ни одно из последних не м. б. следствием остальных—менаду ур-иями будут противоречия. Когда число ур-ий, полученных из наблюдений, больше числа неизвестных, то ур-ия решаются по способу наименьших квадратов (Лежандр, 1806 г. и Гаусс, 1809 г.). Задача этого способа и состоит в том, чтобы уравновесить ошибки, то есть подобрать такие величины неизвестных, при которых эти противоречия были бы наименьшими. (Предполагается, что при наблюдениях не допущено грубых, постоянных или систематических ошибок.) В задачу входит также нахождение меры точности полученных значений величин. Наблюдения бывают кроме того или независимыми друг от друга или условными. В основание способа наименьших квадратов положено требование, чтобы сумма произведений квадратов ошибок на веса была наименьшей.

Уравновешивание прямых наблюдений. Если для определения величины произведены п наблюдений q_x, q₂. ., q_n и их веса суть р_х, р₂, ., р_п, то вероятнейшее значение х величины получают из выражения:

„ _ IPiQA ДРгГ ’

г=п г=п где по Гауссу [р//г]=2 Vib “ Р<·

г=1 i=l

Отклонения v_{ отдельных определений от вероятнейшего значения х находятся из ур-ий:

v₁=x-q₁, v₂=х- q₂, ., υ_η= χ- q_n.

Среднюю квадратич. ошибку ε₀ для единицы веса, среднюю квадратич. ошибку ε_χ от х и средние квадратич ?1, 42

V

ошибки q_n определяют из ф-л:

Г~

от

[ PivJl.

ε.₂ =

V iPii ч

-у

ibC)i ; М (n-l) ’

. ε=^F° ·

Vpl “ ΫΡα ’ ^П ΫΡη

См. Ошибки измерений и наблюдений.

Уравновешивание вспомогательных наблюдений. Измерено п величин q_x, q₂, ., q„ ф-ий u_x, u₂, ., u_n от m неизвестных x, y, z,.

«i=A(®. 2/. z, .),

¹¹2=Ш, y, z, .),

U_n=f_n(x, y, z, .),

причем nl>m. Если из каких-либо m ур-нй найдены приближенные значения x₀,y₀,z₀,. неизвестных, то задача сводится к отысканию поправок Ах, А у, Az,. к этим приближенным значениям, неизвестные же найдутся из соотношений:

х=х₀ + Ах, у=у₀+Ау, z=z₀ + Az,. Если и_{— q₍=А._г, то после подстановок получаем т. н. уравнения ошибок:

А_х=Шо + Дж, Уо + Ау. z₀ + Az,

А₃=h(x<> + Ах, у„ + Ay, z₀ + Az, .) - q₂ Uj)

A_n=f_n(x₀+ Ax, Уо + Ау, z₀ + Az, .)-qJ

Разлагаем f,{x₀ + Ax, y₀ + Ay, z₀ + Az, .) по строке Тейлора, ограничиваясь первыми производными:

А_х=f_x (ж₀, y₀,z₀,.)+ Αχ + _oy Ay -

A % - /₂(.г₀, Уо- z₀,.)-

§Ax + jjfA у.

- 4ι,

• · —

dfn

Αχ -

dfn

dy

Ац /п(Жо> Уо> Zq, · ·.) -Ь q_xВведя обозначения

/<(ж₀. Уо> .)-qi=Vi,

Д» + ··· -7«·

дх ¹

dfi

ду имеем:

Ai= α,Αχ + hi Ay + c_{Az +.: + v_f.

T. о. ур-ия ошибок можно всегда привести к линейному виду.

В частном случае для трех неизвестных х, у, z примем за исходные п линейных ур-ий:

«i=а_хх + Ь_ху + с_хз + а_х 1 м“=а₂х + Ь₂у + c₂z + а₃

!

и_п— а_пх +

откуда:

Λ=«ι·

А₃=и„

<7ι=а_хх + Ь_ху qt=а₂х + b₂у

c₂z ?2

(2)

(3)

А_п — “п~ 4п~ ^ап^х + Ь_пу + o_nz -f 1_п.

причем 1_Х=а,- — q_{; А_х, А₂, ., А„—действительные ошибки. Ур-ия (3) называются у с-ловными. Вероятнейшие значения неизвестных согласно теории вероятностей (смотрите) получатся при условии:

Δ + ΔΙ +. + Ап=minimum, (4)

^:для чего необходимым уравнения:

Л ^i_L А ®4»4-

дх ⁺ ··

/I _1_ Л ^δ/ΐ2 I

условием являются + Л„ ^9А” - 0.

Ог

4-/1 ₌ о

-t- _ду

Л

аГ

dz

= 0,

(40

• (5)

(6)

или на основании уравнений (3):

(а_гх + Ь_гу + <s_xz + li)a_t +

+ (®2* “Ь b₂y + c%z + ϊ₂)α₂ +. +

+ (®и^ж + Ь_пУ + ^cn^z + ln)^an=0 ^c

(ajX + Ь_гу + c_tz + l_t) b, +

+ (α₂ ж + Ь₂у + c₂2 + l₂)b₂ +. +

+ (a_nx + Ь_пу + c_nz + l_n)b_n=0

0<h^x + hy + ^ci^z + h)°i +

+ (а₂ж + Ь_гу + c₂z + l₂)c₂ +. +

+ (а_иж + b„y + c_nz + l_n)c_n=0 _

Собрав отдельно члены с ж, у, z и пользуясь обозначениями Гаусса, имеем:

[aa] х + [аb]у+ [ao]z + [al]=О Ί

[ab] x + [bb]y + [bc]z + [Ы]=0 :

[ac] х + ту + [cc]z+[cl]= 0 )

Эти ур-ия носят название нормальных. Способ решения системы нормальных уравнений, данный Гауссом, состоит в следующем. Найденное из первого ур-ия значение ж подставляют во 2-е и 3-е ур-ия; из первого уравнения новой системы определяют величину у и полученное значение подставляют во 2-е ур-ие, откуда вычисляется z, а затем у и ж. Сущность приема состоит в том, что по исключении каждого неизвестного вновь получаемая система снова носит характер нормальных ур-ий. Числовое решение ур-ий выполняется механически при помощи счетной линейки или логарифмич. номограммы. Для предотвращения ошибок вычислений при составлении и решении нормальных ур-ий суммируют при ур-иях ошибок и при нормальных ур-иях коэф-ты по строкам. По подстановке в условные ур-ия полученных вероятнейших значений х, у, z в правых частях ур-ий будут не нули, а нек-рые величины δ₂,., д_п, называемые остающимися ошибками. В зависимости от последних можно выразить среднюю квадра-тич. ошибку каждого условного ур-ия. Решив т ур-ий, отобранных по числу неизвестных из всех п ур-ий, получим значения неизвестных, точно удовлетворяющие этим ур-иям. Т. о. сумма квадратов остающихся ошибок должна распределиться на остальные п-т ур-ий, то есть ратная модулю упругости). Для нахождения а и т произведено п испытаний, давших п пар значений г и р. Придав формуле вид

lg г=а + m>lg р,

где a=lga, применяем условие (4):

П

S=2 {lg i-(a+m lg р)}²=minimum 1

или на основании (4):

.^0н_я“-0,

да дт ’

Т. е.

2(lgi-a-mlgp)=0

(А)

2 (lg i - а — ж lg р) lg р=О 1

Если принять:

п п п

2lgi=I; 2lgp=P; ^lgi-lg р=.Г_х;

i i i

2(lgp?=I,

1

η

то (т. к. 2^a=^wa) уР-ия (А) примут вид: 1

па + Pm= I

Ра + Р₁т=1₁] ^

откуда

α=

т =

iPi-hP

ηΡχ - «² Ιχη-ΙΡ

ηΡχ-Pt

В частном случае 6 испытаний дали ряд значений риг, причем величины, входящие в ур-ия (А), приведены в след, таблице:

№ опыта	lgp	lg г	lg i * lg P	(Igp)2
1	2,2201081	-3,7723989	-8,3751332	4,9288799
2	2,5224442	-3,4523620	-8,7083904	6,3627248
3	2,6981005	-3,2622777	-8,8019520	7,2797462
4	2,8234742	-3,1292061	-8,8352826	7,9720065
5	2,9201233	-3,0264616	-8,8376409	8,5271200
6	2,9991305	-2,9430105	-8,8264725	8,9947838
	«=16,1833803	/=-19,5857168	Ix= -52,3848216	«1=44,0652612

(w~m)e²=[<5)] или

l ^

У п-т

Пример. Зависимость между деформацией и напряжением при Сжатии материалов, не подчиняющихся закону Гука, выражается эмпирич. ф-лой Баха и Шюле:

г=ар^т,

где г—относительное укорочение образца при сжатии, р—соответствующее полное сжимающее напряжение, т—отвлеченное число, α= А—коэф. сжатия (величина, об-

1380000’

Откуда

a- lg «=- ffH=- 6Д3966, или α=

те=4^=1,066.

2,48975

Итак в данном случае:

г= —— «boss

1380000 Р

Если ур-ия обладают различными весами Рх, р₂, ., р_п, то условием для определения вероятнейших значений неизвестных будет равенство:

ΡχΛ? + ρ₂Λ!+. + ρ_ηΔ 2= minimum. Отсюда нормальные ур-ия примут вид:

[аар]ж + [abp]y + [acp]z + [alp]=0 1 [bap]* + [bbp]y + [bcp]z + [blp]=0 ·

[cap]* + [cbp]y + [ccp]z -f [clp] =0 J

Средняя квадратич. ошибка единицы веса для неравноточных наблюдений выразится следующим образом:

. _{= л}/~

⁰ У п-т

Средние квадратич. ошибки ε₂, ., в_пнаблюдений q_lt q₂, q_n, средние квадратич. ошибки ε^, в_у, ε_ζ неизвестных х, у, ζ находят из равенств:

F — ^ε°, о _ ^ε0, р — ^ε0,

^ει — ’ ®г ^—, ···> ^еп — —

V Pi VPs У Р п

- _ ^ео. р _ ^εο. - __fo.

³⁵ VV» ^у yv_y ^z V* Уравновешивание условных наблюдений. Для определения п непо-средственно измеряемых величин выполнены п наблюдений q_x, q₂, q_n с весами Pi! Ра> ··> Ри> причем измеряемые величины должны удовлетворять те независимым друг от друга условным ур-иям между вероятнейшими значениями х_ъ х₂,., х_п:

^а0 + ®1®1 + ®2*2 +. + й_пХ_п=θ!

Ьо + Ь_хх_х + b₂х₂ +. + Ь_пх_п=О I

Го + П*1 + »2*2 + · · · + г_пх„=0_у

причем т < п. Эти ур-ия берутся в линейной форме. Если в них подставить х_х=q₁+v₁, *2=?2 + · · · > ^хп=Чп + V». то получатся ур-ия случайных ошибок ν_χ, ν₂, ., ν_η:

α,ν

1^ν1 ~τ

«2»-2 + · · · + «Λ + w_a=0j

bi»»i + b₂v₂ -j-. + b_nv_n w_b= 0

»Ά + T₂f₂ +. + r„«„ +=0^

противоречия гс_а, и-_ъ, ., w_m определяются из ур-ий:

= α0 + «ι9ι ж a2?2 + ·	+ О-пЯп
= &ο + ЬрД + b2q2 +.
ί= П + Π9ΐ + r2?2 + ·	• + rnqn J

Для решения рассматриваемой задачи часто применяют способ неопределенных множителей, или способ коррелат, предложенный Гауссом. Значение случайных ошибок v_x, v_t, ., ν_η для [pv²]_min получают при помощи т коррелат к_х, к₂, ., к_т, которые находят на основании те нормальных ур-ий коррелат:

[?]

hi

[£]*· + [?>,+

Случайные ошибки щ, г₂, ляют из следующих ур-ий:

_Vi^?±k₁ + ^k₂ +.

¹ Pl ^{1 1} Pi ²

f*=—fcl+—2+ ··

² i>2 ¹ Ps ² ^

v_n опреде-

r_n=~ki + ~h₂+. +

-k

m;

Vn Vn ^{a 1 1} Vn

Для проверки значения v подставляют в условные ур-ия. По нахождении случайных ошибок определяют вероятнейшие значения искомых величин из ур-ий:

*i=7i + v_t, ж₂=q₂ + v₂, ., х_п= q„ + v_n. Полученные значения х должны удовлетворять первоначальным условным ур-иям. и i

Пример. В плоском тр-ке измерены углы h, В, С с разной точностью: веса измерений суть р_а=1, р_ь=2, р_е~ 3. Сумма углов А, В и С оказалась равной 180°33". Требуется придать к измеренным углам такие поправки, чтобы сумма исправленных углов была равна 180°, а сумма квадратов поправок была наименьшей. В этом случае условное ур-ие имеет вид: а + b + с + 33"=0.

Поправки выразятся через коррелатыт. о.:

α= к, b=2 и с=- ·

Нормальное ур-ие для определения к:

^fc(r + l + 3-) + ^33,=0’

или ~ к 33"=0, откуда к=— 18".

О

Т. о. поправки углов будут таковы: α= — 18", b=- 9" и е=— 6".

Для определения средней квадратичной ошибки б₀ воображаемого наблюдения с весом р=1 служит ф-ла:

где те—число условных ур-ий или дополнительных наблюдений. Средние квадратич. ошибкиε-!, ε₂,ε_η наблюдений^, q₂, .,q_nнаходятся из ф-л:

с _ ^go. о _ ^g0. ε=^е° -

^£1 _ ^2 /— ··» п.

V Pi VV2 V Vn

Для получения средних квадратич. оши-бок ε[, ε₂, ., в_п вероятнейших значений х_х, х₂, ., х_п нужно последние выразить в виде ф-ий от q_x, q₂, ., q_n ^xl=fl(<h, ?2. ···,?»). *2 =92. 9»)> ··» ж»=/»(91. 92.. Чп)·

Диференцирование этих ф-ий дает:

^άχι - щ ^dqi + W*^{dq2 +} rf*2=^d9t + Й dg₂ +

+ τέη^clq”

9/2

⁺ ^^dqn

>.

άχη - dqx dy отсюда:	1 + 1^92+ •••+gL/9»j
	•+K-)	4 :.·· + (	κ«·.)Ί
УК*.)	+Кч		<^ε γ 9ΐηη)
4-У (t>.	)·+Κ·.		(Sr,‘-T

.(7)

величину ошибки в для нек-рых простейших ф-ий, наиболее часто встречающихся в практике. Если а—известная данная величина, не содержащая ошибок, q_t—величины, определенные со средней ошибкой ε₍, то:

= aq; ε=+ αε;, х=aq_xq₂, ε=+ ✓(αί/₂ε₁)² + {aq_xB₂f

a., a

X=- ε=4- —„ ε; α — q2 ’

ж=α Д; e=+ 0.2

^:Д^;

_ε Ί²·

i «I ’

+

^α Уч^а-

Уравновешивание непосредственно измеренных величин, сумма которых дана. &—точная сумма п величин, для определения которых выполнены непосредственные наблюдения q_t, ^2’ ·· Qn с весами р^, р%, р_п, х%, х„—вероятнейшие значения величин и v_ltv .v_n—необходимые поправки к наблю дениям.

1	1	1
Pi [Г	-г-	V = ·" ш

Противоречие w получают из равенства w~S-[q].

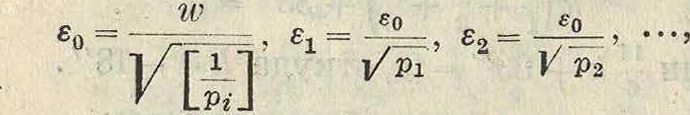
е —*^в~.

^й VVn

Средняя квадратич. ошибка ε вероятнейшего значения х_{ определяется из ур-ия:

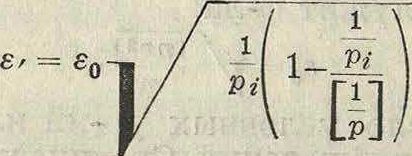
Средняя квадратич. ошибка ε<^?> суммы вероятнейших значений г первых величин равна

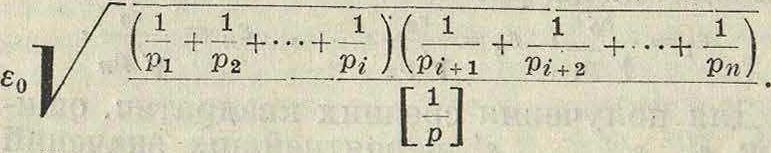
Лит.: Волков А. А., Математич. основания номографии, М., 1911; Блох, Графические методы технич. расчетов, Харьков, 1929; Дешевой М., Графич. умножение и деление и вычерчивание кривых линий, СПБ, 1896; Хаймович Я. М. и Берман Ю. Л., Графические расчеты в машиностроении и технологии, Номограммы и специальные счетные линейки, Киев, 1930; Зильберталь А., Графич. метод анализа периодич. кривых, «Технико-экономич.вестник»,М„ 1926, 2; Б л о х Л. С., Графич. методы построения функций, там ше, М., 1924, 2; О’Рурк, Таблицы умножения для быстрых вычислений, 11 изд., М., 1929; Нейшуллер Л. Я., Таблицы деления многозначных чисел и вычисления процентов, М.—Л., 1929; Лахтин Л. К., Курс теории вероятностей, М—Л., 1924; Марков А. А, Исчисление вероятностей, 4 изд., М., 1924; Иванов А. А., Теория ошибок и способ наименьших квадратов, И., 1921; Гаврилов А. Ф., Практика вычислений, Приближенные вычисления, М., 1926; Придатко С., Практич. вычисления, М., 1924; d’O с a g n e М., Calcul graphique etnomo · graphie, P., 1910; S o.x e a u R., Nomographie ou traiti des abaques, t. 1, 2, P., 1922; P i r a n i M., Graphische Darstellung In Wissenschait u. Technik, B., 1922; Crelle A. L., Rechnentaieln, Berlin, 1923; Tasehenbueh i. Bauingenieure, hrsg. von M. Foerster, 5 Aufl., B. 1, B., 1928; см. также Вычисления приближенные. В. Никаноров.