> Техника, страница 73 > Прецессия

Прецессия

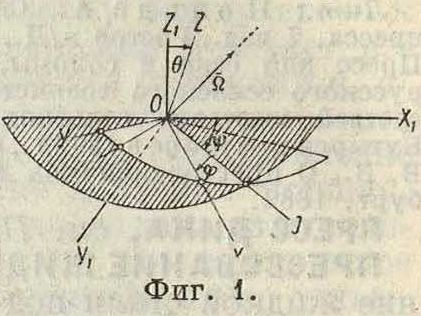
Прецессия, вращение той из главных осей инерции тела, имеющего одну неподвижную точку О (волчка), которая совпадает с осью вращения эллипсоида инерции тела относительно точки О в том случае, если этот эллипсоид представляет поверхность вращения; причем если центр тяжести тела лежит на этой оси и если помимо силы тяжести и реакции точки О никакие другие внешние силы к телу не приложены, то вращение оси происходит около вертикальной прямой, проходящей через О; если же центр тяжести тела совпадает с О, то вращение оси происходит около прямой, проходящей через главный момент количества движения тела относительно точки О. Пусть имеется твердое тело, к-рое может перемещаться около одной своей неподвижной точки О. Для определения положения рассматриваемого тела в пространстве возьмем две прямоугольные системы осей координат, имеющие одно общее начало в точке О, причем пусть одна из них (»!, у_и г_г) будет неподвижной в пространстве, а другая (x,y,z)—подвижной, но неподвижно связанной с перемещающимся телом. Положение последней системы относительно первой, а вместе с тем и положение тела определяются 9 cos углов, образованных осями х, у, z с осями х_г, у_ъ z_x, к-рые, как известно из аналитич. геометрии, связаны 6 ур-иями, так что все 9 cos м. б. выражены при помощи 3 независимых переменных. В качестве последних удобнее всего взять т.н.углыЭйлера, получаемые след, обр.: выбрав неподвижную систему осей х_иу_х, Ζχ, проведем через точку О подвижную в пространстве, но неподвижную в теле произвольную ось z, образующую угол б с осью Ζχ (смотрите фигура 1). Взяв затем прямую OJ, перпендикулярную к плоскости Ζχ Οζ, проведем через последнюю прямую плоскость, перпендикулярную к оси Ог/после чего проведем на этой плоскости через О две взаимно перпендикулярные прямые Ох и Оу. Точно так же проведем через OJ плоскость, перпендикулярную к оси Οζ„ и в последней плоскости возьмем две взаимно перпендикулярные прямые ΟΧχ и Оух. Обозначая углы x_xOJ через у> и JOx через ψ и считая положительными направления их, указанные на фигуре 1, получаем вместе с углом Θ три угла Эйлера у>, φ, Θ. Прямая OJ называется линией узлов, угол у>—у г л о м Π., Θ— углом нутации и φ—у г л о м собственных вращений. Рассматриваемое тело, а вместе с тем и подвижная система осей х,у, z, будет в каждый данный момент совершать нек-рое вращение около некоторой мгновенной оси, имея при этом угловую скорость Ώ (смотрите Механика теоретическая),· проекции которой р, q, г на подвижные оси координат связаны с углами ψ, φ, Θ следующими ур-иями:

р=If sin Θ sin φ + Θ cos φ, 1 q=ψ sin θ cos φ — θ sin φ, > (1)

Г=ψ COS Θ + φ. J

Пусть к телу помимо силы реакции со стороны неподвижной точки О приложена еще система внешних сил F_x, F._z,., F_n, главный момент которой по отношению к точке О пусть имеет проекции на осях, у, z, равные соответственно L, М, N. Если выбрать оси х, у, z так, чтобы они совпали с главными осями инерции тела в точке О, то между L,M,N и р, q, г существуют соотношения, выражаемые следующими ур-иями, называемыми уравнениями Эйлера (смотрите):

L=Af_t+(C-B)qr,

М ⁼ вЩ + (А — С) гр, (2)

N=C% + (B-A)pq, J

где А, В, С суть главные моменты инерции тела в точке О. Из уравнений (1) и (2) м. б. определены р, q, г, a затем и углы ψ, φ, θ в функции времени, если значения p_n,q₀, г₀, ψ₀, 9>о. ®о этих величин, соответствующие некоторому начальному моменту времени, известны. Пусть в частности на движущееся тело во время его движения действуют только его сила веса G и реакция точки О и пусть ось Ζχ будет выбрана вертикальной, а подвижные оси х, у, z выбраны совпадающими с главными осями инерции тела в точке О. Допустим далее, что центр тяжести тела лежит на оси z и что координаты этой точки

относительно подвижных осей суть£, η, ζ, а относительно неподвижных осей ξχ,ηχ,ζχ- Т. к. живая сила W тела равняется в этом случае (смотрите Эйлера уравнения)

W=l (Ар“ + Bq² + Or²), (3)

то, исходя из того, что диференциал живой силы равняется сумме элементарных работ всех внешних сил, приложенных к телу, получаем:

з d (Ар“ + Bq² + Or²)=- тд άζ_χ, (4)

где m—масса всего тела. Интегрируя (4),

имеем:

Ар“ + Bq* + Сг“=- 2 mg ζχ + С_г, (5) где Oj—нек-рая произвольная постоянная интеграции. В рассматриваемом случае сумма моментов всех внешних сил, действующих на тело, по отношению к оси z равна О, вследствие чего главный момент количества движения тела относительно той же оси есть величина постоянная, то есть проекция вектора главного момента количества движения на ось Ζχ есть величина постоянная. Т. к. проекции главного момента количества движения относительно точки О на оси х, у, ζ суть Ар, Bq, Or (смотрите Эйлера уравнения), то, обозначая cos углов, образованных осями х, у, ζ с осью Ζχ, через у₁₍ γ₂, γ_Ά, имеем:

Αργχ + Вду₂ + Cry ₃=С₂, (6)

где С₂—нек-рая постоянная.

Так как

Ух=sin Θ sin ψ, γ₂=sin Θ cos φ.,

Уз=cos θ, (7)

то из (6) и (7) имеем:

Ар sin 0 sin φ + Bq sin Θ cos φ 4-

+ Cr cos Θ=C₂. (8)

Рассмотрим далее еще более частный случай, когда эллипсоид инерции (смотрите) относительно точки О есть поверхность вращения около оси ζ, содержащей также и ц. т. тела. В этом случае мы очевидно имеем:

А=В; ξ=η=0 (9)

и

ζχ=ζ cos θ. (10)

Из (5) и (8) имеем тогда, принимая во внимание (9) и (10):

А(р“ + q*) + Сг“=— 2 mg ζ cos θ + Οχ, (11) A sin θ(ρ sin φ + q cos φ) 4- Cr cos 0=C₂. (12)

Помимо этого из 3 ур-ия (2) имеем (т. к. Л^г=0):

(13)

г=Const=г₀.

Из (11), (12) и (13) имеем далее:

р“ 4- q²=Сх - с; cos Θ, (14)

(р sin φ -г q cos φ) sin θ=CJ — Gpo cos Θ, (15) r=r₀, (16)

где

c;=

-Ой

2 mg ζ

c-

p" O

- X

Ca =

следнего. Подставляя в (14), (15), (16) значения р, q, г из равенств (1) находим после соответствующих преобразований:

sin² Θ (ff ) + (!)²= с; - сг cos Θ, (18)

C₂r₀ cos д, (19)

(20)

(Ιψ _{Λ п}, άφ

«cos Θ + _Έ=Τ₀.

Положив cos θ=а и решая совместно (19) и (20), получаем:

dp С" dl ‘

άφ

ж=^г°

1 —а²

a(Cf -С./о®) jT—а²

(21)

(22)

Подставляя (21) в (18), имеем:

(ty=(Ci-Oxa)( 1-a²)--(C,-C₂r₀a)·=f(a). (23)

При помощи эллиптич. интеграла можно из последнего ур-ия определить а в функции времени t, а затем из (21) и (22) определить и ψ, φ в функции ί, после чего движение тела полностью определено. Не прибегая однако к эллиптич. интегралам, можно уяснить себе характер движения тела, исходя из следующих соображений. Из ур-ия

(21) видно, что ^ становится равной нулю с:;

при α= γ—, то есть при последнем значении а

άψ

dt

меняет свой знак. Если

> 1, то а,

будучи равным cos Θ, не может достичь значения так что менять свой знак не сможет и следовательно угол ψ лиоо все время только возрастает либо только убывает, то есть линия узлов OJ вращается все время в одну и ту же сторону. Если же

C

С"

< 1, то а может стать равным

^о^Г0

άψ,

так что gj· может в действительности стать равной 0; угол ψ будет в этом случае попеременно то увеличиваться до определен-

_Г|1 da

ных пределов, то уменьшаться. Так как -j-

должна иметь вещественное значение, то /(а) должна иметь во всяком случае положительный знак, так что при α=_7ίΓ^?-< 1,

С„г о имеем из (23):

^С2^Г о

1-

^с!_у

> 0. (24)

^C2^r°J

Из последнего же неравенства следует, что должно иметь место неравенство с: С"

С1>:

(25)

если

^С2^Г0

(17)

Нетрудно усмотреть, что постоянные С и С₂положительны и зависят только от самого вращающегося тела, а постоянные Сх и С₂зависят от начальных условий движения по-

< 1. Изменение угла у и определяет т. н. прецессионное движение тела или сокращенно его П. Из (23) нетрудно усмотреть,что f(a) будет отрицательной при значениях а, равных —1 и +1, и что /(a) положительна при начальном значении α= а₀ (т. к. в противном случае производная | была бы мнимой) и при α= + оо. Т. о. видно, что имеются три вещественных корня для /(а),

лежащие в интервалах: (-1, а₀); («„, 4-1); ( + 1, + оэ), так что получаем:

/(а)=Gi(a — а_г)(а₂— а)(а₃ — а). (26)

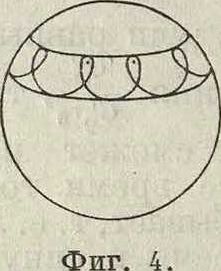
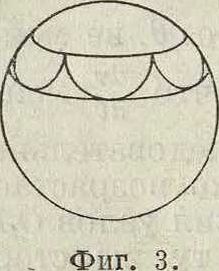
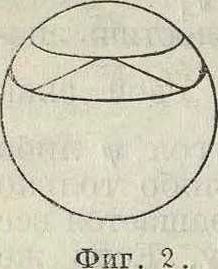
Т. к. α= cos Θ, то |а |<1, т. ч. а₃— а есть существенно положительный множитель. Для того чтобы f(a) была положительной, необходимо следовательно, чтобы имела место одна из следующих пар неравенств: либо а — cij < О И а₂ — а < О либо а — а_х > 0 и а₂ — а > О, то есть чтобы либо а, > а > а_г либо а_х < а < а₂. Т. о. для того чтобы f(a) оставалась положительной, необходимо, чтобы а оставалась в пределах от а_г до а₂, то есть чтобы cos Θ находился в пределах от cos θ_χ=a_t до cos б₂= α₂. Угол θ следовательно будет изменяться в пределах от в_г до 0₂. Изменение угла Θ и определяет т. н. нутационное движение тела или сокращенно его н у т а ц и ю. Из предшествующего явствует, что ось Οζ описывает коническ. поверхность, заключенную между двумя конусами, имеющими общую вершину в О, общую ось Oz_r и углы при вершине, равные 2 θ_± и 2 0₂. Если описать около О как около центра шаровую поверхность и проследить за движением точки пересечения оси е с этой поверхностью, то траектория точки представляет один из типов кривых, изображенных на фигуре 2, 3 и 4, причем в общем эти кривые незамкнуты. При а_г= а₂ оба предельных конуса сливаются в один; в этом случае П. называется

регулярной. Если сообщить телу начальную угловую скорость вращения значительных размеров около оси вращения, близко совпадающей с осью г, то шаровой пояс, заключенный между предельными конусами, становится столь малым, а ось ζ столь быстро перемещается от одного из них к другому,что получается впечатление, будто бы имеет место регулярная П.; в этом случае П. называется псевдорегулярной. Если центр тяжести тела, обладающего всеми вышеуказанными свойствами, совпадает с неподвижной точкой О, то прецессионное движение происходит в общем не около вертикальной оси г_ъ как в вышеприведенном случае, а около оси I, проходящей через О и совпадающей с вектором L главного момента количества движения тела относительно О, который сохраняет в этом случае постоянными как свою величину, так и направление. Тело в рассматриваемом случае совершает регулярную П., так что ось ζ тела описывает круглую конич. поверхность, называемую конусом П. около оси I. Неподвижная аксоида (смотрите) представляет собой круглый конус, имеющий ту же ось I и ту же вершину О, что и конус П.; подвижная аксоида представляет собою круглый конус, имеющий с неподвижной аксоидой общую образующую и общую вершину и осью которого является ось ζ тела. Вектор мгновенный уг ловой скорости Ω направлен по обшей образующей. Движение тела происходит так, как будто бы неподвижно связанная с телом подвижная аксоида катится равномерно без скольжения по неподвижной аксоиде. Если относительное вращение тела около оси ζ происходит в ту же сторону, что и вращение оси ζ около оси I, то подвижная и неподвижная аксоиды расположены внешним образом друг по отношению к другу, а неподвижная аксоида находится внутри конуса П.(фигура5). В этом случае рассматриваемая регулярная П. называется эпициклоидаль-н о й. Если же относительное вращение тела

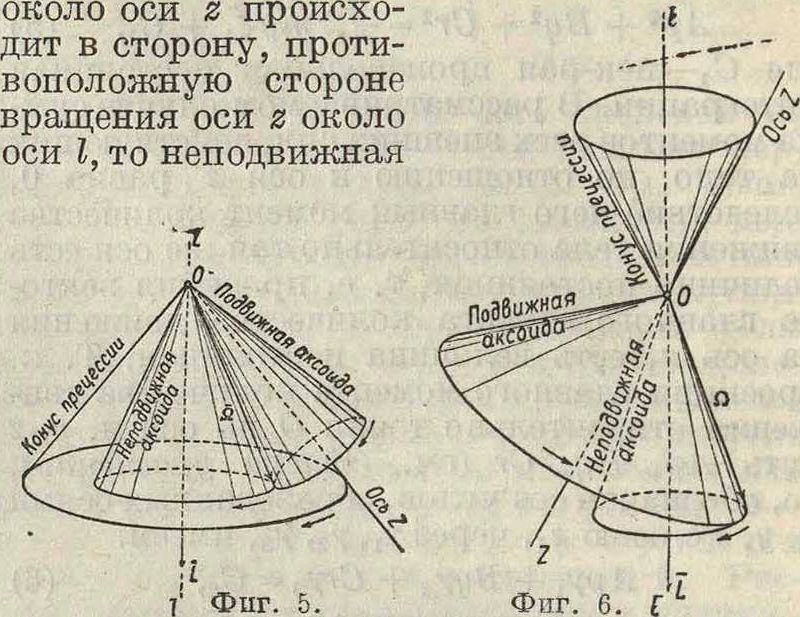
аксоида находится внутри подвижной аксоиды (фигура 6), а конус П. и неподвижная аксоида, имея общими оси и вершины, расположены внешним образом по отношению друг к другу. В этом случае регулярная П. называется перициклоидальной. Явления П. и нутации играют крупную роль при движении волчка (смотрите), при всех технич. применениях последнего, в баллистике, астрономии и тому подобное.

Лит.: см. Волчок, Механика теоретическая, Баллистика. М. Серебренников.

П. в баллистике, то есть в приложении к изучению вращательного движения продолговатого артиллерийского снаряда, имеет то же значение, что и в движении оси симметрии волчка, описывающей некоторую коническую поверхность с вершиной в точке опоры волчка, но т. к. снаряд является волчком, не имеющим точки опоры, вершина прецессионного конуса находится в его ц. т. Величина П. артиллерийского снаряда определяется углом между осью фигуры снаряда и касательной к траектории ц. т. снаряда в данный момент. Рассматривая вращательное движение артиллерийского снаряда на· основе теории волчка, следует иметь в виду наличие наряду с силой тяжести еще и силы сопротивления воздуха. Если же при решении задачи ввести в рассмотрение еще «пару Магнуса» (смотрите Роторные суда), допустить, что в действительности и имеет место, расположение п. т. снаряда не в точности на его оси, что эллипсоид инерции снаряда относительно его ц. т. не является точным эллипсоидом вращения и что начальная скорость ц. т. и начальная угловая скорость вращения снаряда образуют нек-рые, хотя и весьма малые, углы с осью его фигуры, то становятся совершенно очевидными и чрезвычайная сложность рассмотрения прецессионного движения сна-

ряда и невозможность точного до конца решения задачи, в общем ее виде, средствами •современного математического анализа. В соответствующей литературе имеется ряд попыток освещения вопроса о прецессионном движении артиллерийского снаряда, но почти все они имеют в виду частные случаи стрельбы, преимущественно прицельной, и к тому же содержат те или иные допущения с целью упростить решение поставленной задачи. Диференциальные уравнения вращательного прецессионного движения снаряда с необходимыми комментариями—см. Баллистика. Экспериментальное изучение прецессионного движения артиллерийского снаряда также встречает ряд трудностей, проистекающих гл. обр. от сложности обстановки, в которой происходит явление полета снаряда. Простейшим средством экспериментального изучения П. может служить стрельба большим числом выстрелов по листам картона, устанавливаемым на пути движения снаряда. По полученным в листах пробоинам можно составить в той или иной мере точное представление о величине П. Само «обой понятно, что постановка такого опыта стрельбы по картонным щитам пригодна лишь для изучения П. на начальном участке •траектории, то есть вблизи дула орудия.

Лит.: Петровиче., О вращательном движе-пии продолговатого снаряда около его центра тяжести, Петроград, 1920; Лен дер Ф., Теория волчка, ч. 1—Общая теория волчка в элементарном изложении, Ленинград, 1927; De Sparre, Mouvement <le projectiles oblongs autour de leur centre de gravity, Paris, 1911. В. Шелков.

П.в астрономии. Притяжения Луны, •Солнца и планет на Землю вызывают движение земной оси в пространстве, к-рое разлагается на две составляющие: прогрессивное .движение по конусу с углом между образующей и осью конуса, равным наклонно-сти эклиптики к экватору, и периодом ок. 26 000 лет, называемое П.,имелкое периодич. колебание, называемое нутацией (смотрите). П. состоит в движении точки весеннего равноденствия навстречу годичному движению Солнца, что укорачивает длину тропическ. года по сравнению со звездным годом. Скорость р движения точки весеннего равноденствия в год называется постоянной Π. П. влияет на координаты светил, меняя их долготу на величину р, оставляя неизменной широту. Влияние П. на прямое восхождение •а и склонение <5 более сложно и обычно учитывается при помощи разложения в ряд:

Δα= At + ® f^{* 2} + Ci⁸,

Δδ=At + ~t² + Ci»,

где t—разность эпох в годах; А иА называются годичной П. по прямому восхождению и склонению, В и В—вековым изменением (variatio saecularis), С и С—третьим членом П. Годичная П. выражается так: А ;= т + п sin a tg <3^ A=те cos а, где т и п—величины, зависящие от р. Для звезд, расположенных близ полюсов мира, разложения слишком медленно сходятся и приходится пользоваться для учета П. более сложными тригонометрич. ф-лами.

Лит.: Иванов А., Теория прецессии, СПБ, 1899; Newcomb S., A Compendium of Spherical Astronomy, New York, 1906; «Astronomical Papers of the American Ephemeries», v. 4, Wsh.; см. лит. « CT. Параллакс. А. Михайлов