 > Техника, страница 74 > Продольная сила
> Техника, страница 74 > Продольная сила
Продольная сила
Продольная сила, осевая сила, линия действия которой параллельна оси стержня. Если точка приложения П. с. S находится в точности на оси стержня, то она вызывает в стержне только растягивающие или сжимающие напряжения в зависимости от ее направления. В сечениях, достаточно удаленных от точки приложения силы S (на расстояниях не менее наибольшего размера поперечного сечения стержня), эти напряжения распределяются равномерно по площади поперечного сечения стержня и их величина
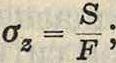
вблизи же точки приложения сил эта равномерность в распределении напряжений нарушается т. наз. местными напряжениями, возникающими у точек приложения сил и весьма быстро уменьшающимися по мере удаления от этих точек. Ф-лой (1) можно пользоваться при расчете растянутых или сжатых стержней; не надо только забывать, что для последних, при достаточно большой сжимающей силе S, прямолинейная форма стержня может сделаться неустойчивой, и стержень подвергнется продольному изгибу (смотрите Устойчивость). Если П. с. приложена не в точности на оси стержня, а с эксцентриситетом е (фигура), то стержень будет изгибаться и в нем кроме напряжений по формуле (1) возникают изгибающие напряжения от действия момента Se. Здесь мы сталкиваем-
ся с одновременным действием изгиба и растяжения или сжатия. Сюда же относятся все те случаи, когда на стержень 7или балку действуют П. с. и одновременно поперечные силы, дающие момент Ж, вызывающий изгиб стержня или балки. Если П. с. мала по сравнению .с критич. силой Рк для данного стержня (смотрите Изгиб продольный), то можно при расчете стержня просто складывать напряжения от. П. с. с напряжениями от момента Ж. Наибольшее нормальное напряжение в плоскости поперечного сечения стержня будет:
S, м_
FW
(2)
где W—момент сопротивления, а Ж—изгибающий момент в наиболее опасном сечении. В случае длинных гибких стержней, когда П. с. не мала сравнительно с критической, формула (2) не применима; надо принять во внимание влияние П. с. на величину прогиба., а через эту величину и на величину изгибающего момента. Очевидно, что растягивающая П. с. уменьшает первоначальный прогиб от поперечных сил, а сжимающая увеличивает их. Точное решение задачи даже при простейших нагрузках приводит к сложным ф-лам, но можно указать простые приближенные ф-лы, дающие вполне удовлетворительные результаты и применимые к случаю любой заделки концов балки, а также и к балкам переменного сечения. Оказывается, что наибольший прогиб стержня при наличии П. с.
t- i£s* (3)
где f0—прогиб от действия только момента Ж; а2= р—отношение П. с. к критич. силе для данного стержня. Знак + относится к случаю растягивающей, знак — к случаю сжимающей П. с. Дополнительный момент от действия П. с.
S=ifb· №
т. о. для полного изгибающего момента от действия поперечной нагрузки и П. с. имеем
Μ + Τ&· ©
В частном случае при одновременном действии П. с. и поперечной изгибающей силы Р, приложенной по середине пролета, наибольший изгибающий момент
м = щ(1 + о^д. (6)
В случае П. с. и поперечной нагрузки q, равномерно распределенной по всему пролету балки,
,03а а ж=*г (х + т
±а
Г
(7)
В обоих случаях 1-й член дает изгибающий момент от одних лишь поперечных сил, а 2-й член, зависящий как от поперечных сил, так и от П. с., дает увеличение изгибающего момента от действия П. с. Здесь мы встречаемся с довольно редким в сопротивлении материалов случаем, когда принцип сложения сил неприменим; из ф-л (5—7) видно, что изгибающий момент, а следовательно и напряжения при одновременном действии поперечных и продольных сил зависят от П. с. не линейно, то есть напряжения непропорциональны П. с., а зависят от нее более сложно. Прогиб f тоже не пропорционален силе
S—закон Гука нарушен, хотя деформации и происходят в пределах упругости. Зная М, можно из ф-лы (5) найти напряжения и рассчитать балку или стержень. Благодаря нелинейной зависимости М от П. с. при расчете на прочность вместо обычной ф-лы s, м р
F
(R—допускаемое напряжение), приходится пользоваться более сложными. Так, при одновременном действии П. с. и поперечной Р, приложенной по середине пролета, необходимо пользоваться ф-лой
Ι,823ηα2
Г < R’
F 4W
L ± Па“ )
(8)
а при П. с. и равномерно распределенной по всей балке нагрузке q кг/см—ф-лой
S, ql
F ^ 8W 1
1
1,028Па2 1 ± Па2 ]
(9)
где п—коэф. безопасности. Вообще, как указывает Тимошенко, при расчете .стержней на одновременное действие поперечных и П. с., следует брать для допускаемых напряжений обычное значение, но в расчетных ф-лах надо множитьП. с. на коэф. п, равный принятому запасу прочности. Из выражений (3—9) видно, что в случае коротких стержней, для которых а мало, влияние П. с. на изгиб ничтожно. Ее роль возрастает с увеличением гибкости стержня, то есть с уменьшением критич. силы. Для растянутых стержней а может быть более 1 (на практике а2 редко превышает 10). Для сжатых же стержней, если а приближается к. 1, то есть если П. с. приближается к критич. силе для данного стержня, то в выражениях (3—9) знаменатель 1 —а2 стремится к 0. Следовательно, весьма малая поперечная сила может вызвать весьма большие прогибы. При а=1 ф-лы (3—9) теряют свой смысл. Ошибка при применении приближенных ф-л (3—9) для самых неблагоприятных случаев нагрузки и закрепления концов не превосходит немногих процентов.
Лит.: Тимошенко С. П., Сопротивление материалов, 8 изд., гл. M, М.—Л., 1929; его ж е, Теория упругости, ч. 2, § 8—13, П., 1916; Ф а н-д е р-Ф лит А., Об одной задаче строительной механики, «Изв. Собрания инженеров путей сообщения», СПБ, 1903, 10—12; его же, Применение нормальных координат, «Известия Киевского политехи.ин-та», Киев, 1909; 3 а в р и е в К., Сопротивление стержней сложному продольному изгибу, «Вестник Об-ва технологов», СПБ, 1913, 16. А. Динник.