Пропеллер

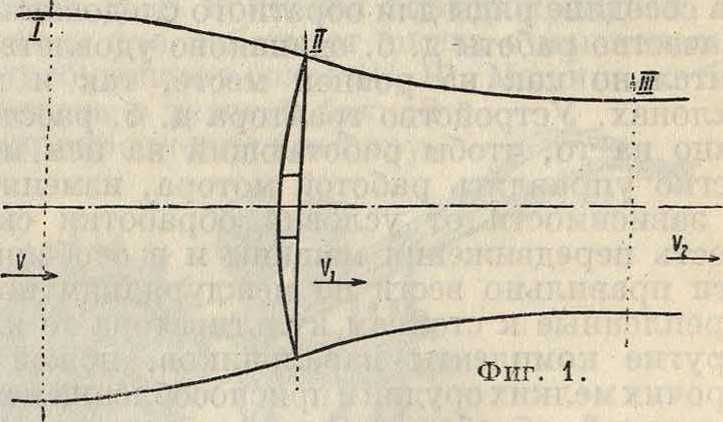
Пропеллер, аппарат для получения тяги в податливой среде. К П. относятся например гребной винт (смотрите Воздушный винт), различного рода колеса с клапанами и тому подобное. Теория П. основана на общих теоремах механики и в силу своей схематичности не зависит от конструктивных особенностей данного П. В приложении к винту она дает некоторые общие выводы, которые м. б. использованы для предварительных расчетов. Основой для расчета П. является теория идеального пропеллера Фруда и Финстерваль-дера. Теория _>та базируется на следующих предположениях: П. образует струю жидкости (фигура 1) с равномерным распределением скорости по поперечному сечению струи; жидкость предполагается идеальной и несжимаемой. В относительном движении скорость жидкости далеко перед П. равна поступательной скорости V пропеллера, в плоскости пропеллера скорость жидкости равна V₁=V+v, в струе далеко за пропеллером F₂=V+ v₁ (скорости V и V, называются скоростями подсасывания и отбрасывания). Давления в струе далеко перед и за П. равны атмосферному. На границе струи скорость претерпевает разрыв непрерывности. На воронкообразное тело, заключенное между границами струи и плоскостями 1 и III, отстоящими весьма далеко от плоскости П., действует только тяга пропеллера Р, т. к. давление на границах струи всюду равно атмосферному. По теореме о количестве движения получим

Р=т (F₂ - F)=mv_lt

где т—масса жидкости, протекающая через плоскость П. в единицу времени. Так как давления в плоскостях I и III равны, то

вся работа П."уходит на создание живой силы в струе. Живая сила в сечении I будет Д-², в сечении III --4. Следовательно 2 2

мощность будет

_ т V% ¹ i~ 2

mV² 2 ⁼

(Γ + ϊ)

или

= Р (f + у)

П. движется относительно жидкости со скоростью Fj, следовательно сила Р производит в единицу времени работу PF_t. Приравнивая оба выражения, получим уравнение v₁=2v, что дает теорему Финстервальдера: скорость отбрасывания равна двойной скорости подсасывания. Так как т=qFV_х, где

ρ—массовая плотность жидкости, F=~ —

площадь, ометаемая П., то из предыдущих ур-ий получим:

o(i + pV-=b=— ·

Величина В называется коэфициентом нагрузки на ометаемую пропеллером площадь; она играет основную роль в теории П. (смотрите Аэродинамика, расчет самолета). Полезная секундная работа будет PV, следовательно идеальный кпд будет

^Va У1 ι+νϊψΜ

-Зависимость η_α от В представлена графически на фигуре 2. Последнее ур-ие показы-

0.5

Фигура 2.

вает, что выгоднее увеличивать диаметр П., -т. к. при этом уменьшается В и увеличивается η_α, однако предел этому увеличению в действительном П. кладет мощность трения, возрастающая с увеличением диаметра.

В случае П., работающего на месте (идеальный геликоптер F=0), ф-лы получат вид: P=mV_i=mv₁, F₂=2F₁=2t>,

mVjj Pvi _ py

2 2 ¹ ’

m=qFV_v

Отсюда

P=2 qFV,

T_{=2 qFV^?{.

Вводя относительный кпд ч_отн., равный отношению идеальной мощности к действительной мощности Т, имеем;

Т =

2gFVl

Чотн.

.Исключая Fj, получим

„з ^Р3 _Т2=2 qF

или, вводя диаметр D и мощность N в №, получим ф-лу,

Р=(F« · 94,2 ·

носящую название ф-лы Вельнера. Величина относительного кпд v_omu. обычно равна Ό,50 -г 0,70 в случае аэропланных винтов, подымаясь выше в случае специальных ге-ликоптерных винтов.

Дальнейшее обобщение теории идеального П. применительно к гребному винту получим, приняв, что жидкость в струе П. вращается, причем в относительном движении угловая скорость вращения далеко перед П. будет Ω, в плоскости пропеллера Ώ=Ω — ω и далеко за пропеллером й₂== Ω₁ — ω₁(Ω — угловая скорость вращения винта). Применяя теорему о моменте количества движения, получим М — 1со_и

где I—момент инерции жидкости, проходящей в единицу времени сквозь пропеллер (предполагается, что жидкость вращается как твердое тело). С другой стороны, мощность ΜΩ расходуется на полезную работу PV₂ и создание живой силы в струе за винтом, равной ~ Следовательно

ΜΩ=PV + + ~1г= PV + Р ~ + М ^ ·

Подставляя I=Щ²- =

и исключая М.

Fi, v_lt получим ур-ие

(Ω - ωlR*=2 BF²,

откуда _

_ωι^Ω-]^~^ψ.

rr. 4BV2

T. к. величина весьма мала по сравнению с Ω², то приближенно, с большой степенью точности,

2BV2

— am ‘

Кроме того из ур-ия баланса энергии имеем

m(s-9)=p(f + !),

откуда кпд идеального П. (идеальный кпд)

й-“¹_ PV __ _2

^% ма~ а

V +

»1

= Va

где

Va =

^ωι

γ+^νΛ l+Fi + 2 В"

η=^Ω~ ² - 1 - -^V- - 1 _

4 P

Ω ЙД2 ρίΏ2χ)2

Коэф. у_и, оценивающий потери от живой силы вращения, носит название окружного (тангенциального) кпд в отличие от осевого (аксиального) кпд η_α, оценивающего потери на живую силу поступательного движения. Потери в действительном П. оцениваются относительным кпд у_отн, Таким образом полный кпд η будет

V ⁼ ViVomu. ⁼ УаЧиЧотн.·

Величина _тн_ у воздушных П. колеблется в небольших пределах около 0,8. Главное изменение в кпд происходит за счет изменения η_α.

Из предыдущего видно, что в плоскости П. относительная скорость на конце лопасти имеет составляющие F_x по оси и Ω_XR по окружности. Отношение этих скоростей очевидно определяет режим винта. Обычно берут пропорциональную величину Λι= Vi λ.

= _n^_D=—, где Я—относительная поступь винта (смотрите Воздушный винт). Т. к. спектр скоростей в плоскости винта целиком определяет все величины, характеризующие его работу, весьма удобно все величины относить к скоростям в плоскости винта. Стандартные коэф-ты винта а и β при этом условии приобретают вид

= ^р я - ^Т

¹ ρη^Β¹’ ¹ ρηξΒό

Вместо мощности Т удобнее брать вредную мощность

ΓΤΊ _ ГП_ PVl

^ ^J Пи и соответствующий ей коэфициент

^р^· впр

Связь с обычными стандартными коэфициен-тами будет

ββρ.

η3^ Vomu.)·

Преимущества новой системы коэф-тов перед старой обнаруживаются в следующем

т. Э. m. XVIII.

обстоятельстве: при пропорциональном изменении ширины лопастей винта стандартные коэф-ты а и β изменяются при заданном А не пропорционально ширине лопасти. У новых коэф-тов а, и β_βρ. эта пропорциональность при заданном Я, соблюдается. Поэтому при пересчете характеристик какого-либо винта при изменении числа лопастей в п раз или и-кратном изменении ширины лопастей приходится сначала переходить на новые коэф-ты, изменять их пропорционально п и затем по полученным коэф-там переходить опять на стандартные коэф-ты. Порядок пересчета таков: имеются а, β я η при заданном А; высчитываются последовательно: осевой кпд основного винта 2 2 На

1 + У1+2 в

1 +

V·

1+;

окружной кпд основного винта

1 4

Ϊ*.

идеальный кпд основного винта Vi=Va · Пи>

относительный кпд основного винта

^Тотн. - _щ ’

относительная поступь в плоскости винта коэф. тяги в плоскости винта а

^а1⁼⁼ ~^2’

•и коэф. тяги в плоскости измененного винта α= а_гп.

Затем подсчитываются стандартные коэ-фициенты измененного винта по формулам:

осевой кпд

2 <

Л-

окружной кпд

Vu — л ’

1 -f- — Cl i

лз 1

идеальный кпд

= Va * Vu>

относительная поступь

λ=νΆ>

коэфициент тяги

a=a nl,

коэфициент полезного действия

V=ni· W. коэфициент мощности

Т. о. имеем в итоге все коэф-ты, необходимые для расчета измененного винта.

Весьма удобны диаграммы серийных испытаний винтов, пересчитанных на новые коэф-ты. Эти диаграммы строятся как обычно, но вместо коэф-тов Я, β я η берутся Я₁, а и г)_отн. С помощью таких диаграмм можно подобрать наивыгоднейшую ширину лопасти винта на какое угодно задание.

Теория идеального П. с большим успехом применяется также для расчета винтов в комбинации тендем. В этом случае винты стоят взатылок. Обычно считают, что передний винт работает как изолированный;

задний винт работает в струе, отбрасываемой передним винтом, то есть при скорости

F₂=F]/T+2В.

Характеристика режима у него будет не К=а я;=—²=Кроме того кпд заднего винта следует относить к скорости V, а не к скорости V₂. Поэтому определенный по А^ кпд ??2 следует помножить на отношение Таким образом кпд заднего винта в комбинации тендем будет η₂=г/₂ ~,

то есть будет меньше, чем у того же винта, но· изолированного. Бблыную точность получим, учитывая также и изменение окружных скоростей. Тогда характеристика заднего винта будет уже

3_ з У Ω ±(0ι

где знак (+) относится к случаю противоположного вращения винтов, знак (—) к. случаю одинакового направления вращения. Отсюда видно, что винты тендем всегда следует делать с противоположным вращением, т. к. при этом повышается величина λ₂, а следовательно и кпд заднего винта. В нек-рых случаях выигрыш может достигать величины 4—5%. Можно также учесть (грубо) влияние заднего винта на передний, снизив величины η я β для него приблизительно на ¹/_i поправки, полученной для заднего винта.

С нек-рыми изменениями теория идеального П. прилагается также к расчету ветряков, вентиляторов и тому подобных аппаратов. Во всех случаях приложения теории идеального П. следует твердо помнить основные предположения, которые положены в основу теории, особенно предположение о наличии ясно выраженной струи. В про-тивоположном случае очень легко прийти к совершенно неправильным выводам. В случае идеального ветряка имеем суживающуюся струю. Поэтому скорости подсасывания и отбрасывания будут иметь отрицательную величину; однако теорема Финстер-вальдера имеет место и в этом случае. Понятие кпд теряет свой обычный смысл и вместо него в теории ветряков пользуются понятием коэф-та использования энергии ветра. Этот коэф. определяется как отношение получаемой с ветряка полезной мощности к живой силе массы воздуха, проносимой со скоростью V через ометаемую ветряком площадь. Он получается из выражения.

5-НМУ·

Из этого выражения видно, что максимальный коэф. использования равен получается при у=·

В заключение приводим таблицу для осевого кпд v_a в зависимости от нагрузки на ометаемую площадь В.

В	Va	В	Va
0,00	1,0000	1,60	0,6559
0,20	0,9161	1.80	0,6360
0,40	0,8540	2,00	0,6180
0,60	0,8055	2,20	0,6017
0,80	0,7655	2.40	0,5868
1,00	0,7321	2,60	0,5730
1,20	0,7032	2,80	0,5604
1,40	0,6781	3,00	0.5486

Лит.: Жуковский Н.Е., Теоретик, основы воздухоплавания, М., 1925; Юрьев Б. Н., Воздушные гребные винты (пропеллеры), ч. 1, «Труды ЦАРИ», вып. 10, М., 1925; Ветчинкин В. П., Теория гребных винтов, М., 1926; Винен Ф, К а р-м а н Ф. и Л е р у Б., К теории воздушных винтов, пер. с нем., Л., 1926; В e с е л о в с к и и Μ. Н., Новая система характеристик, коафициентов гребного винта, «Война итехвика», М., 1927; tt lauert Н., The Elements of Aerofoila. Airscrew Theory, Cambridge, 1926. В. Ведров.