> Техника, страница 74 > Пространственные механизмы

Пространственные механизмы

Пространственные механизмы, ме ханизмы, движение звеньев которых происходит не параллельно общей плоскости.

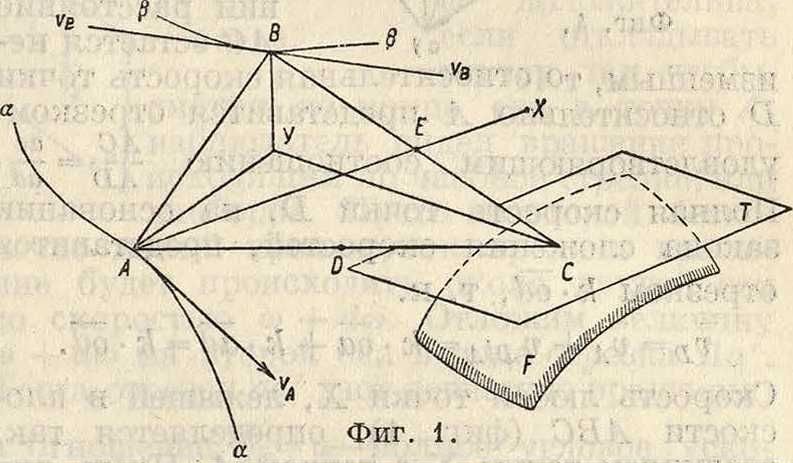
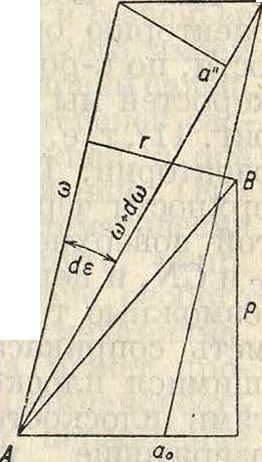
Кинематический анализ. Т. к. положение твердого тела в пространстве определяется положением трех его точек, то следовательно движение звена П. м. должно быть задано движением трех его точек. Пусть даны скорость v_A и траектория а—а точки А звена. АВС (фигура 1). Зададимся произвольной траекторией точки В. Пользуясь теоремой о проекциях скоростей концов отрезка

на отрезок, выбираем произвольную точку о за начало плана скоростей (фигура 2) и через точку о проводим луч, параллельный v_A;

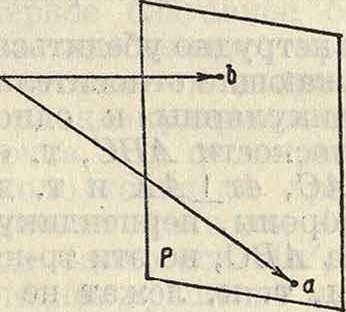
Фигура 2.

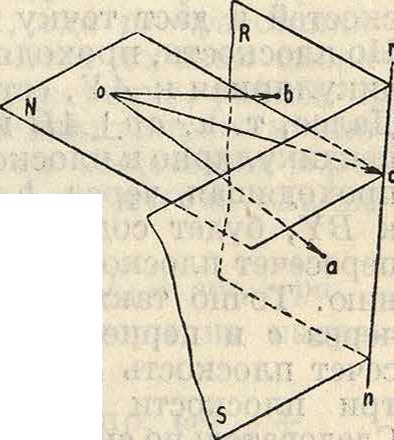
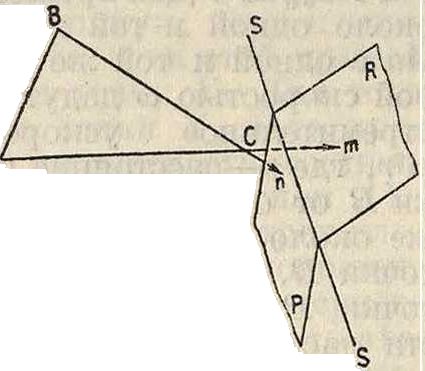
на этом луче откладываем отрезок оа так, что ν_Α=к оа, где к—масштаб отложения. Через точку а проводим плоскость Р, перпендикулярную к АВ. Далее, зная траекторию β—β, через точку о проводим луч, параллельный VB плоскость Р пересечет этот луч в точке Ь, и скорость точки В выразится v_B=k-ob. Для определения скорости точки С проводим через точку а плоскость S, перпендикулярную к АС (фигура 3), а через точку Ь плоскость R, перпендикулярную к ВС. Конец скорости точки С должен лежать на линии пересечения п—п плоскостей S и Л. Из построения ясно, что нельзя задаться для точки С произвольно выбранной траекторией ее движения, т. к., проводя направление скорости точки С, касательное к траектории, можно не получить пересечения этого направления с направлением п—·п, т. к. две прямые в пространстве в общем случае могут не пересекаться. Следовательно можно рассматривать только поверхность, на которой будет находиться точка С за все время ее движения; пусть это будет поверхность F (фигура 1). Т. к. направление скорости точки С лежит в плоскости Т, касательной к поверхности, то, проведя через точку о (фигура 3) плоскость N, параллельную плоскости Т, находим в пересечении этой плоскости с прямой п—п точку с и т. о. скорость точки С выразится: vc~k-oc. Итак

Фигура з. для полного кинематич. анализа звена в пространстве надо знать траектории двух точек и поверхность, по которой движется третья точка. Скорость точки D, лежащей на прямой АС (фигура 1), определится из условия, что отрезок к -ас (фигура 4) есть относительная скорость в движении точки С относительно точки-И, а т. к. при этом относительном движении расстояние АС остается неизменным, то относительная скорость точки D относительно А представится отрезком,

АС ас удовлетворяющим соотношению ^ ·

Полная скорость точки D, на основании закона сложения скоростей, представится отрезком k-od, т. к.

Vd*=v_a + vDi_A=k-oa + k-ad=k· od.

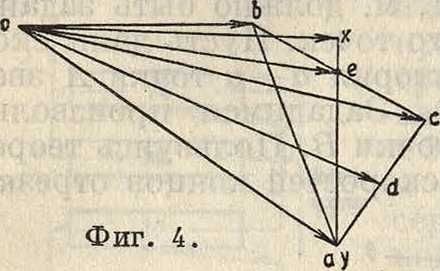
Скорость любой точки X, лежащей в плоскости АВС (фигура 1), определяется так: соединяем точку×с точкой А. Пусть луч АХ пересечет прямую ВС в точке Е. Скорость точки Е определяется тем же приемом, как и скорость точки D, из соотношения

be BE г,

ес⁼ЁС Соединив теперь о и е, находим положение точки х на луче ае из соотноше-ния ~=~. Скорость точки×будет равна

vx=k.ox. Из построения нетрудно убедиться, что все отрезки, изображающие относительные скорости, перпендикулярны к одноименным отрезкам в плоскости АВС, то есть аЬХАВ, Ьс_ _ВС, ас_ _АС, ах _АХ и т. д. Т. о. тр-к abc имеет стороны, перпендикулярные к сторонам тр-ка АВС, но эти тр-ки не являются подобными, т. к. лежат не в параллельных плоскостях.

Для определения скорости какой-либо точки, лежащей вне плоскости АВС, проведем через точку А (фигура 1) прямую, перпендикулярную к плоскости аbс, и на этой прямой возьмем произвольную точку Y. Для того чтобы найти скорость точки Y, надо провести через точки a, ft и с плоскости, соответственно перпендикулярные к сторонам AY, BY и СУ. Точка пересечения этих трех плоскостей и даст точку У в плане скоростей. Но плоскость, проходящая через а и перпендикулярная к AY, есть сама плоскость abc. Далее, т. к. ab±AB и abJ_AY, то аb перпендикулярно к плоскости ДВУ и плоскость, проходящая через b и перпендикулярная к BY, будет содержать направление ab и пересечет плоскость abc по этому направлению. Точно также плоскость, проходящая через с и перпендикулярная к СУ, пересечет плоскость abc по прямой ас, то есть все три плоскости пересекаются в точке а. Следовательно скорость точки У выражается тем же самым отрезком оа, как и скорость точки α(ν_γ=ν_Λ). Но т. к. точка У была на прямой ДУ выбрана произвольно, то и все точки прямой ДУ будут иметь скорости, равные скорости точки А. Итак для определения скорости какой-либо точки твердого тела надо провести через эту точку прямую, перпендикулярную к плоскости abc, отметить точку пересечения этой пря- |

мой с плоскостью АВС и найти на плоскости abc точку, соответствующую точке пересечения. Луч из точки о, соединяющий найденную точку, даст величину и направление скорости искомой точки. Т. о. концы векторов скоростей всех точек твердого тела лежат в плоскости abc. Назовем ее скоростной плоскостью, пучок векторов, выходящих из точки о,—с к о р о с τη ы м п у ч ко м, а всю систему—п л а н о м скоростей в пространстве.

Исходя из основного положения, что все точки твердого тела, лежащие на прямой, перпендикулярной к скоростной плоскости, имеют одну и ту яге скорость по величине и по направлению, движение твердого тела в пространстве можно представить так: пусть прямая F—F (фигура 5), перпендикулярная к скоростной плоскости, имеет равные скорости, представляемые вектором k.of. Да

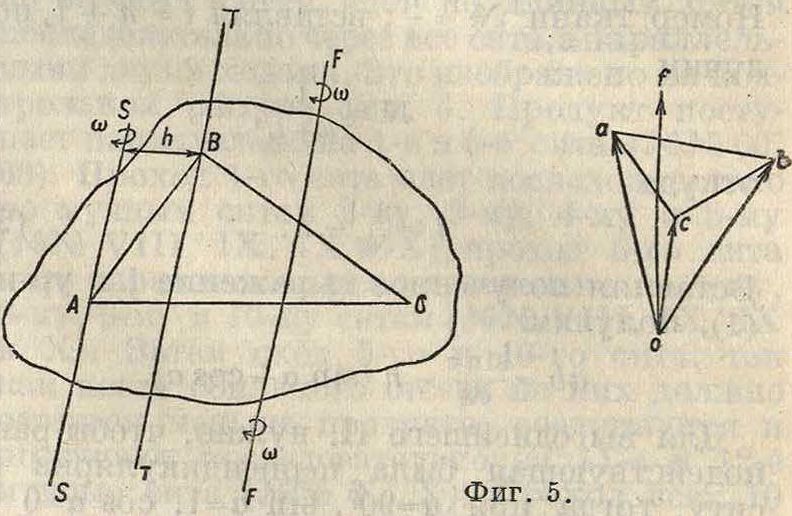
дим всем точкам твердого тела скорости, равные и противоположные скорости v_f. Тогда прямая F—F останется неподвияг-ной, а тело будет иметь только вращательное движение. Отсюда следует, что всякое-движение твердого тела м. б. представлено сложенным из поступательного со скоростью какой-либо точки тела и вращательного около оси, проходящей через эту точку и имеющей для данного момента вполне определенное направление, независимое от выбора точки твердого тела. При этом скорость поступательного перемещения будет различной в зависимости от выбора точки, через к-рую проведена ось вращения; угловая же скорость вращательного движения будет для каждого данного момента одна и та же. Возьмем например за основную точку А и проведем через нее ось S—S, перпендикулярную-к плоскости аbс. Скорость точки В будет результирующей из скорости точки А искорости вследствие вращательного движения около оси S—S. Из плана скоростей видно, что скорость точки В есть результирующая векторов оа и ab; вектор об и будет очевидно представлять слагающую скорости В вследствие вращательного движения около оси S—S, то есть, обозначив скорость точки В относительно А через —ν_Βι_Α, имеем:

v_sIa=a>_Ah=k ab,

где ω_Α—угловая скорость вращения около оси S—S, h—расстояние точки В от этой же оси, к—масштаб отложения. Если вместо точки А выбрать точку В и ось Т—Т, то:

^vaIb=~vbI_A=^{к bа}=^ωΒ (- h), т. к. расстояние от оси S—£ до точки В ра-

вно расстоянию точки А до оси Т—Т вследствие параллельности осей S—S и Т—Т, откуда очевидно, что ω_Α=ω_Β=ω. Величина <о носит название угловой скорости мгновенного вращения. Из скоростного пучка ее величина определяется

ab

<oh=kab, откуда ω= — к, но т. к.

h есть величина проекции отрезка ЛВ на скоростную плоскость, то:

аЬ ₇ bс

ω=к пр. АБ/пл. abc пр. ВС/пл. abc

Все возможные поступательные скорости тела представлены в виде скоростного пучка в плане скоростей.

Очевидно, что в теле будет содержаться ось, все точки которой имеют наименьшую поступательную скорость. Для ее определения находим в скоростном пучке вектор, имеющий наименьшую величину; это будет перпендикуляр on, опущенный из точки о на плоскость abc (фигура 6). Находим точку N на плоскости АВС, соответствующую точке п, и через нее проводим ось R—R, в в А

Ф.1Г. 6.

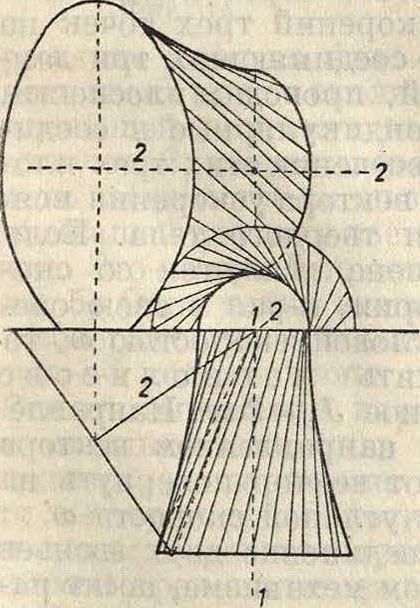
перпендикулярную fк abc. Очевидно, что движение тела можно представить как скольжение около оси R—R со скоростью v_n== к-on и вращение с угловой скоростью ω. Ось R — R носит название оси мгно-венноговращенияи скольжения. Геометрич. место осей мгновенного вращения и скольжения есть поверхность, которая носит название неподвижной аксои-д ы, а геометрич. место прямых в теле, последовательно служащих осями, называется подвижной аксоидой. Движение тела за конечный промежуток времени м. б. сведено к качению и скользкеиию подвижной аксоиды по неподвижной (фигура 7). На чертеже представлены аксоиды, в частном случае задания движения, в проекциях Монжа. Однополый гиперболоид вращения с осью 2—2 катится и скользит по гиперболоиду вращения с осью 1—1.

Для определения ускорений точек твердого тела можно воспользоваться тем условием, что двизкение твердого тела можно представить, как поступательное перемещение со скоростью точки А и движение около А. Тогда для точки В твердого тела АВС .(фигура 8):

Jb=Ja + JbU>

где Ja^JbiJbU—ускорения точек А, В и В

ФПГ. 7.

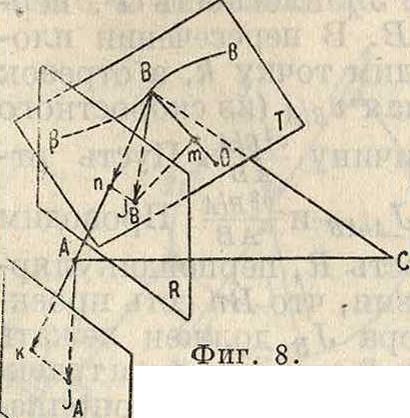
относительно А. Для определения величины JbIa проводим через точку А ось мгновенного вращения (фигура 9) и на этом направлении отложим угловую скорость ω мгновенного вращения в нек-ром масштабе в виде отрезка Аа. Направление этого вектора зависит от принятого условия, например ω положительна, если откладывать вектор так, чтобы, смотря из конца его в точку А, наблюдатель видел вращение происходящим по часовой стрелке, или наоборот. Пусть во второй бесконечно малый промежуток времени вращение будет происходить около другой оси со скоростью со + άω. Отложим величину со -f άω на второй оси в виде отрезка Аа. Тогда отрезок аа даст девиацию вращения,

аа а отношение=а—полное угловое уско рение. Вектор аа разлагаем на два направления: аа" и аа" ± Аа. С точностью до малых второго порядка можно написать: аа"=άω и аа"=code, откуда

~ άω. de

α= -г- + ω —: di dt

направлении

σ

Первое слагаемое берется в оси мгновенного вращения и второе — в направлении, перпендикулярном к нему.

Точка В в своем движении около точки А вращается сначала около оси Аа, а потом около оси Аа, но последнее врашение м. б. разложено на вращение около оси Аа и вращение около оси Дй₀||вя· Два вращения около одной и той же оси Аа с одной и той же угловой скоростью ω дадут осестремительное ускорение а>²г, где г—расстояние точ- _Фигки В от оси Аа. Вращение же около оси Аа даст добавочную скорость точки В, равную apdt, где р— расстояние точки В до оси Аа₀. Этот добавок скорости даст добавочное ускорение, равное ар и направленное перпендикулярно к плоскости АВа₀. Вектор ар называется в р а-

щательным образом:

ускорением. Таким

J_Bj_A=ω²τ -{- ра или j _в=J_А 4- oj²t pa. Запроектируем все эти векторы на направление отрезка АВ:

^ПР· JbUb ^{= u}Ρ· JaIab + ^ΠΡ· ^ω2>’ΛΒ +

+ πρ. ρα_ΛΒ,

но πρ. ρα_ΛΒ =0, так как pa ± ΑΒα₀,

v²B/A

πρ. оАг_лв =

AB

v²b!a

AB

следовательно пр. J_в/_лв=пр. JaIab +

для всякого движения точки в пространстве. Т. о. ускорение точки В легко м. б. опреде-

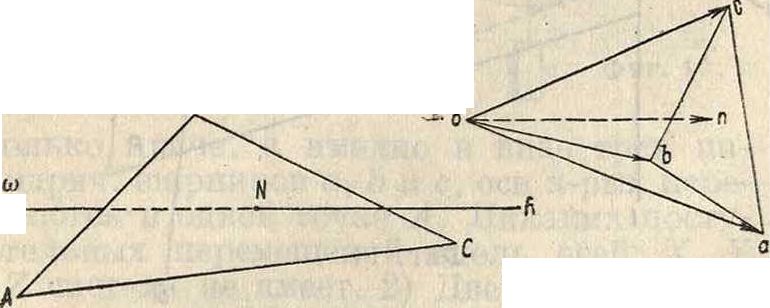
лено, если известно ускорение точки А и траектория β—β точки В (фигура 8). Пользуясь теоремой о проекциях, проводим через конец вектора J_A плоскость Р, перпендикулярную к АВ. В пересечении плоскости Р с АВ находим точку к, а отрезок Ак даст пр. J_A/_AB· Зная v_Bj_A (из скоростного пучка) находим величину у“в1а

Ав

Пусть от резок Вп есть сумма J_Ai_AB и Проводим через точку п плоскость R, перпендикулярную к АВ. При условии, что Вп есть проекция J_B, конец вектора J_B должен лежать в плоскости R. С другой стороны, зная траекторию β—β точки В, проводим соприкасающуюся плоскость Т и находим радиус кривизны ОВ точки В. Откладываем на радиусе ОВ отрезок Вт, равный центростре мительному ускорению JⁿB точки В:

„2

"У. ОВ

Из точки. т ведем в соприкасающейся плоскости перпендикуляр к ОВ. Пересечение этого перпендикуляра с плоскостью R и даст конец вектора ускорения J_B точки В. Для нахождения ускорения точки С находим по предыдущему проекции этого ускорения на направления ВС и АС, пусть это будут отрезки Сп и Cm (фигура 10). Через точки пит проводим плоскости Р и R, соответственно перпендикулярные к сторонам АС и ВС. На линии £—S их пересечения должен лежать конец вектора J_c—ускорения точки С. Далее необходимо рассмотреть, какую траекторию описывает точка С на поверхности, по которой она перемещается. Из плана скоростей мы имеем вектор ее скорости v_c(фигура 11), то есть направление, касательное к ее траектории. Проводим нормаль СЛ^Т к поверхности через точку С. Находим сечение этой поверхности плоскостью, содержащей v_c и CN, и центр кривизны О этого сечения. Возможные траектории для точки С будут иметь соприкасающимися плоскостями плоскости, содержащие v_c; какая-нибудь из этих плоскостей пересечет поверх- Фигура Ю. ность по некоторой кривой с радиусом кривизны тем же самым, что и радиус кривизны той неплоской кривой, для которой проведенная плоскость в данный момент является соприкасающейся. Если к нормальному сечению провести плоскость под углом а, то радиус кривизны ρ этого сечения выразится:

ρ=СО cos а,

то есть геометрич. место центров кривизны есть окружность, описанная на СО, как на диаметре, и содержащаяся в плоскости, перпендикулярной к v_c, т. к. все радиусы кривизны перпендикулярны к v_c. Далее имеем

_rn vc

откуда т П 2

J cQ ^{= v}c·

Вектор v_c известен из плана скоростей, и очевидно, что если на каждом векторе ρ

отложить Jс, то произведение J% на ρ будет величиной постоянной. Т. к. концы ρ лежат на окружности, проходящей через С, то концы J” будут лежать на инверсии этой окружности, которая в данном случае будет

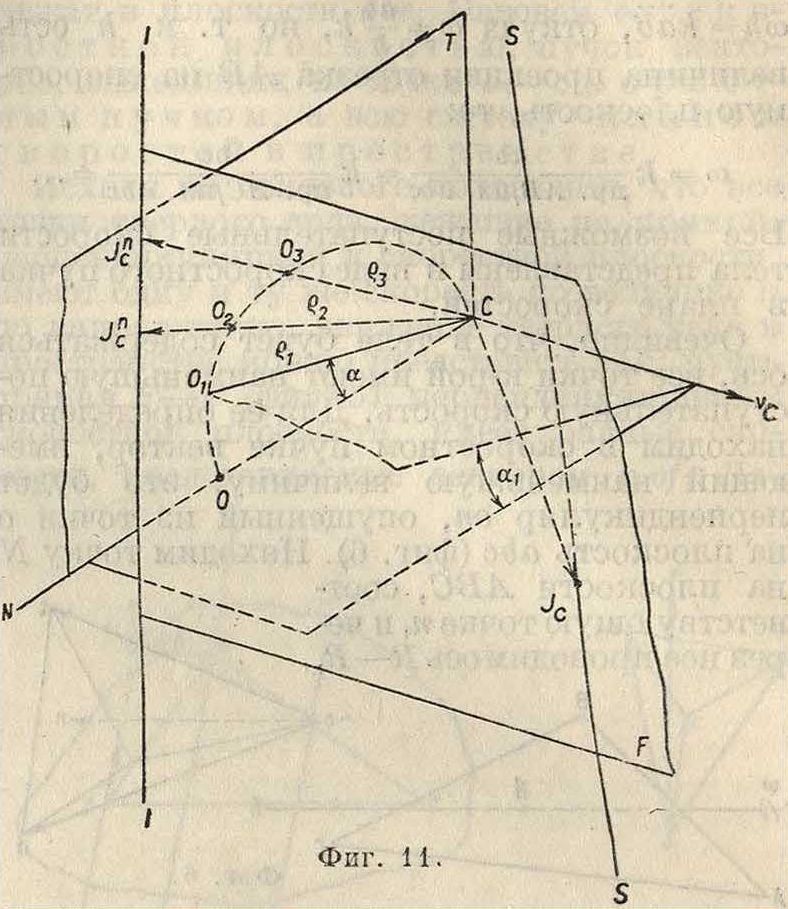
прямой J—J в виду того, что центр инверсии лежит на окружности. Тангенциальное ускорение точки С будет направлено перпенди-кулярно к Jс> то есть перпендикулярно к плоскости Т, и геометрич. местом этих тангенциальных ускорений будет плоскость F, параллельная v_c и проходящая через прямую J—J. Конец полного ускорения точки С должен лежать в этой плоскости, но т. к., с другой стороны, он должен лежать на прямой S—S, то конец этого вектора J_с лежит в точке пересечения прямой S—S и плоскости F. Зная ускорения трех точек А, В и С твердого тела, ускорение любой четвертой точки находят путем применения теоремы о проекциях. Для этого через концы найденной проекции ускорений трех точек на направления лучей, соединяющих три данные точки с четвертой, проводим плоскости, соответственно перпендикулярные к соединяющим лучам. Пересечение этих трех плоскостей дает конец вектора ускорения всякой четвертой точки твердого тела. Если какая-либо точка звена движется со скоростью V по траектории, которая в свою очередь вращается с угловой скоростью со, то необходимо определить кориолисово ускорение, равное J_k=2ων. Направление J_k совпадает с направлением вектора скорости V, рсли этот вектор повернуть на 90° по направлению угловой скорости со.

Конструктивное соединение двух звеньев П. м., как и в плоском механизме, носит название кинематической пары (смотрите Механизмы). С аналитич. точки зрения, кинематич. парой можно назвать совокупность условий связик-рыми определяется относительное движение двух сцепленных между собой тел. Связи, или ограничения в движении одного звена относительно другого, м. б. выражены в виде ур-ий связи или же представлены геометрически. Геометрич. представление о парах было принято Чебышевым, Сомовым. Рело, Грасгофом, а в дальнейшем развито Гохманом, Ассуром и Малышевым. Дадим наиболее часто встречающиеся случаи кинематич.пар в пространстве. 1) Два звена имеют одну общую точку. В этом случае кинематич. пара имеет 3 условия связи. Примером такой пары может служить т. н.шаровой шарнир (фигура 12). Звено 1 имеет возможность вращаться около трех осей X, Y и Z в пространстве. Точно такие же движения имеет звено 1 относительно звена 2 (фигура 13), но здесь эта кинематич. пара изображена условно не

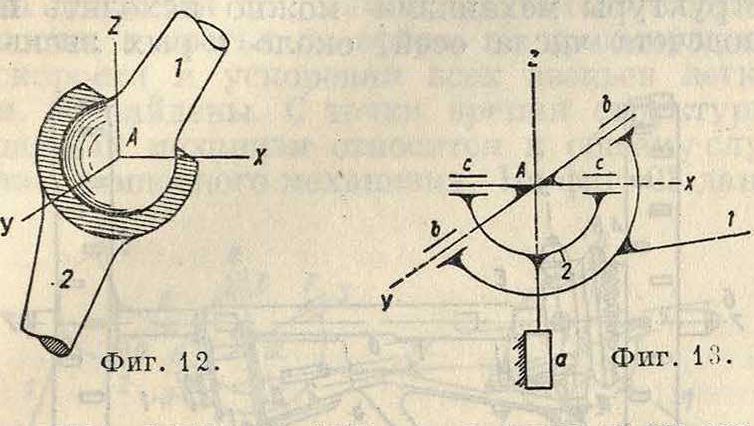
сколько иначе, а именно в виде трех ци-линдрич. шарниров а, b и с оси которых пересекаются в одной точке А. Никаких поступательных перемещений вдоль осей X, Y и Z система не имеет. 2) Две точки одного звена неподвижны по отношению к другому звену. В этом случае кинематич. пара имеет 5 условий связи. Примером такой пары служит цилиндрический шарнир ("фигура 14). Звено 2 может только вращаться около оси о—о. Никаких перемещений вдоль оси о—о звено 2 не имеет. Условное его из-

Фигура 14. Фигура 15.

обряжение дано на фигуре 15. 3) Одна точка одного звена может скользить по линии, принадлежащей другому; этому случаю соответствуют 2 условия связи. 4) Две точки одного звена могут скользить по линии, принадлежащей другому звену; здесь 4 условия связи. Это—случай пространственного ползуна. 5) Одна точка звена может скользить по поверхности, принадлежащей другому звену,—1 условие связи.

Все эти кинематич. пары м. б. выполнены или отдельно или же в комбинации. Так, в примере, указанном на фигуре 12 и 13, одно и то же перемещение звена м. б. выполнено или одним шаровым шарниром (фигура 12) или системой трех цилиндрич. шарниров (фигура 13). Пользуясь тем условием,что каждый механизм должен обладать только одной степенью свободы, можно, подсчитывая условия связи в звеньях и парах, производить анализ механизма с точки зрения правильности его структуры, например анализируя механизм фигура 16, видим, что он имеет 5—6 цилиндрич. шарниров и одну поступа тельную пару (в точке А). Считая только подвижные звенья, получаем: пять звеньев имеют каждое по 9 неизвестных координат, а всего 45 неизвестных. Каждое звено имеет

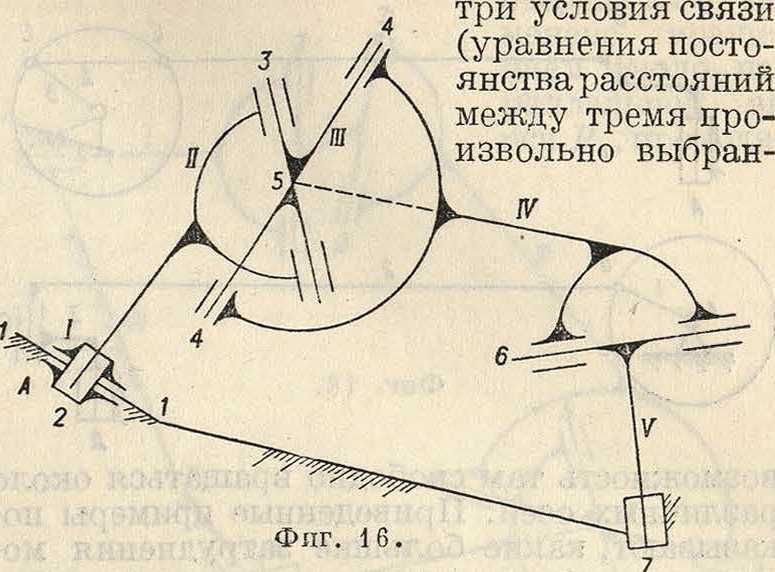
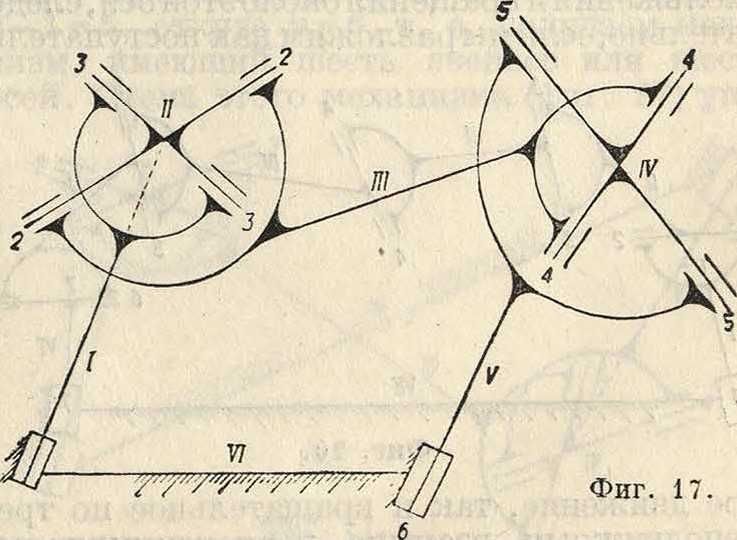
ными точками), а 5 звеньев имеют 3x5=15 условий связи. Пять цилиндрич. шарниров имеют каждый по 5 условий связи, а всего 25. Поступательная пара имеет четыре условия связи. Таким обр. общее количество к условий связи будет: к=25 + 4 + 15=44. На 45 неизвестных имеем 44 ур-ия, то есть система имеет (45 — 44) одну степень свободы и является механизмом. Практика показывает, что не всегда такой подсчет дает окончательное решение задачи, например анализируя механизм, указанный на фигуре 17, имеем на 5 движущихся звеньев 9 х 5=45 неизвестных координат. Шесть цилиндрических пар дают 5 х 6_=30 условий связи и 5 звеньев дают 3x5=15 условий связи. Всего имеем на 45 неизвестных 30+15 =45 условий связи, то есть система, как не имеющая степеней свободы, должна бы быть неподвижной, а она имеет вполне определенное движение. Очевидно, что в данном случае математически одно уравнение должно исчезнуть, например обратиться в тождество, вследствие особого расположения осей или звеньев механизма. Обращение ур-ий в тождества может происходить в различных случаях (одинаковость углов между осями шарниров, пересечение осей шарниров, совпадение траекторий и т. д.). Возможен и обратный случай, когда неправильно сконструированный механизм все-

таки работает благодаря целому ряду конструктивных допущений; так,механизм передачи ΐί решетам веялки (фигура 18) имеет 3 звена, или 27 координат, 12 условий связи в звеньях и 20 условий связи в парах, всего 32 условия связи на 27 координат, то есть не

является механизмом с точки зрения мате-матич. анализа. Работа его на практике возможна только при условии, что шипы В и С помещены в свободные отверстия и имеют

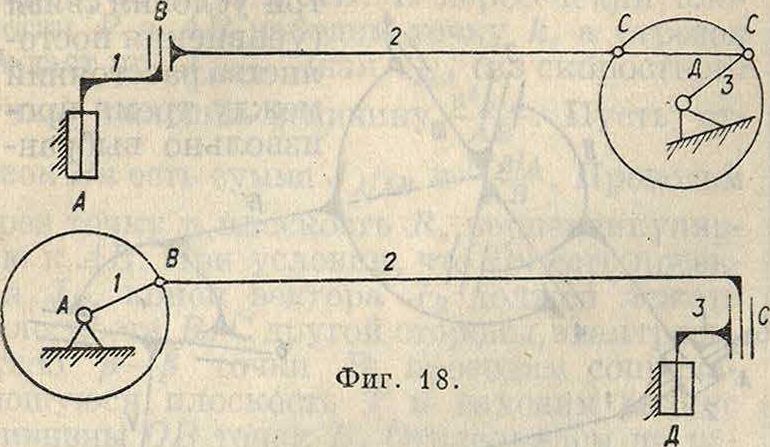
возможность там свободно вращаться около различных осей. Приведенные примеры показывают, какие большие затруднения могут встретиться при анализе структур П. м. Вот почему на практике при Составлении схем механизмов удобнее пользоваться обобщениями и выводами из них, данными Грасгофом.

Общий случай шарнирной цепи. Предположим, что требуется определить, какое число звеньев должна иметь цепь с непараллельными и непересекающимися осями в пространстве для того, чтобы быть цепью принужденного движения, то есть при неподвижном одном звене и произвольном движении другого остальные звенья должны двигаться определенным образом. Если назовем звенья через А, В, С, ., N и движение каждого звена относительно соседнего—

через а, β, у сительно N

, V, где а—движение А отно--движение В относительно А ит.д. Если звено N неподвижно, то абсолютное движение какого-либо звена С будет слагаться из а, β, γ,. Очевидно, что и движение звена N будет слагаться также из движений а, β, у,., :.ν. Но, как известно, абсолютное движение какого-либо звена слагается из поступательного перемещения вдоль оси мгновенного вращения и скольжения и вращения около этой оси, следовательно, если мы разложим как посту патель-

Фигура 20.

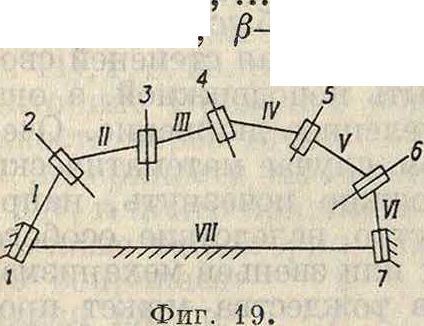
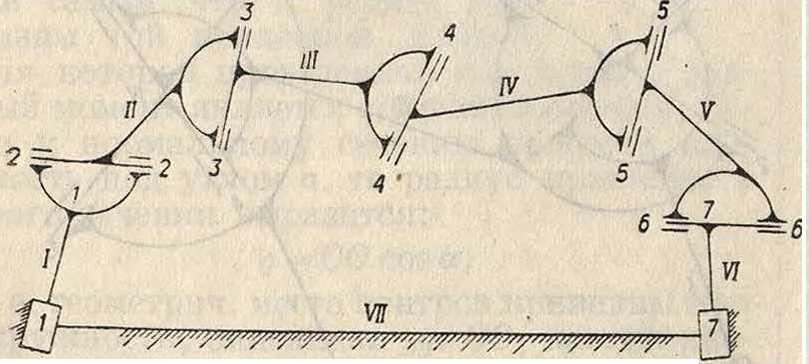
ное движение, так и вращательное по трем неподвижным взаимно перпендикулярным осям, то получим 6 слагающих движений звена. Для рассматриваемого звена Ν, движение которого складывается из движений α, β, γ, ., эти последние должен быть между собой связаны так, чтобы давать требуемые 6 движений звена Ν, то есть в нашем случае удо влетворять 6 условиям его неподвижности. Но из п возможных движений одно является произвольным и неподлежащим никакому условию, следовательно остается η — 1 движение, подлежащее шести условиям, и для определенности решения задачи необходимо, чтобы и—1=6, откуда п=1, то есть в общем случае пространственная шарнирная цепь должна иметь 7 звеньев. Схемы общего случая семизвенного механизма даны, на фигуре19 и 20.Из чертежа ясно,что 7 звеньям механизма соответствуют 7 осей вращения или, как это было показано выше, 7 звеньям соответствуют 7 относительных движений. Следовательно при определении правильности структуры механизма можно исходить из подсчета числа осей, около которых звенья

анализе механизма (фигура 16) видно, что он имеет 7 осей, то есть структура его правильна.

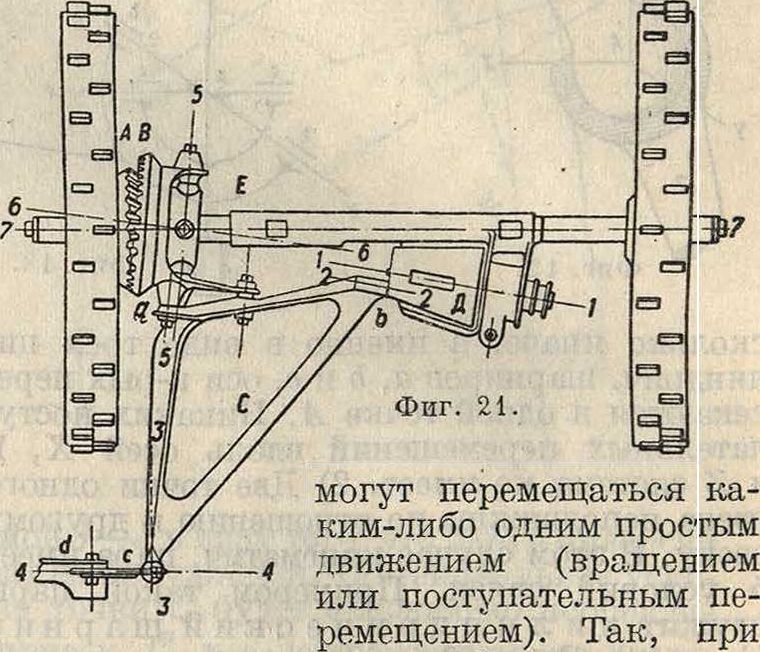
На фигуре 21 дан механизм передачи к ножу косилки. Шестерня А, вращаясь вместе с хр-довым колесом, одновременно находится в соприкосновении с шестерней В. В одновременном зацеплении находится 11 зубцов. В виду разницы в количестве зубцов (шестерня А имеет 46 зубцов, а шестерня В 48 зубцов) при повороте шестерни А по отношению к шестерне В на 2 зуба шестерня В делает 1 оборот. В точке Е шестерня В

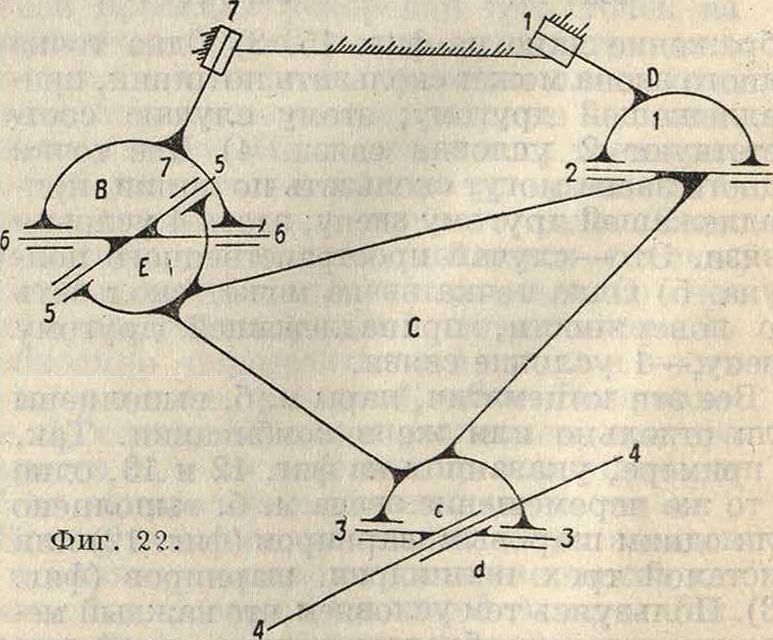
связана с осью 7—7 шарниром Гука. Шестерня В жестко связана с рамой С,точка с которой связана с ножом d. Точка с рамы имеет колебательное движение вдоль оси 4—4 и вращение около оси 3—3. Точка b рамы сидит на оси 2—2 и описывает окружность в пло-

скости, перпендикулярной к оси 1—1. Схе-матич. изображение этог.о механизма дано на фигуре 22. Кинематич. исследование данного механизма м. б. произведено так: звено D, вращаясь около оси 1—1, описывает всеми своими точками окружности, перпендикулярные к оси 1—2, и следовательно все точки оси 2—2, принадлежащей также и звену С, описывают окружности; точка с одновременно принадлежащая звену d и звену С, движется по прямой 4—4; точка Е, принадлежащая одновременно звеньям В я С, будет центром сферы, по которой движутся точки оси 5—5, принадлежащей звену С; следовательно звено С движется так: одна его точка движется по прямой, другая по окружности, а третья по сфере; по предыдущему скорости и ускорения всех звеньев легко м. б. найдены. С точки зрения структуры данный механизм относится к общему случаю семиосного механизма. На фигуре 23 дана

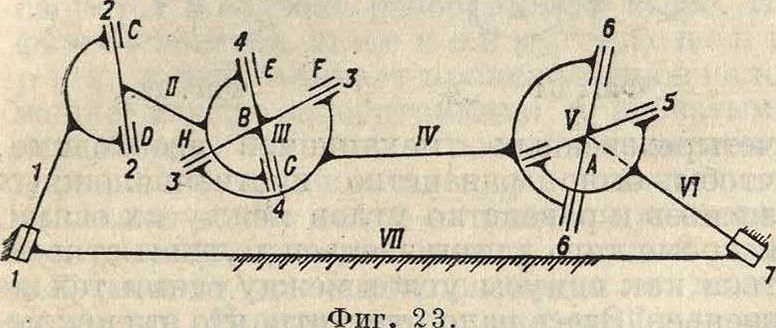
схема механизма мотовила. Точка А механизма остается неподвижной, точка В движется по сфере, т. к. расстояние АВ постоянно, следовательно звено II движется точками С и D по окружностям, перпендикулярным к оси 1—2, а точкой В, ему также принадлежащей,—по сфере радиуса АВ, т.е. его скорости и ускорения легко по предыдущему находятся. Зная скорость точки В, легко найти скорости точек Е и G, потом II и F и т. д. На фигуре 24 дана схема механизма

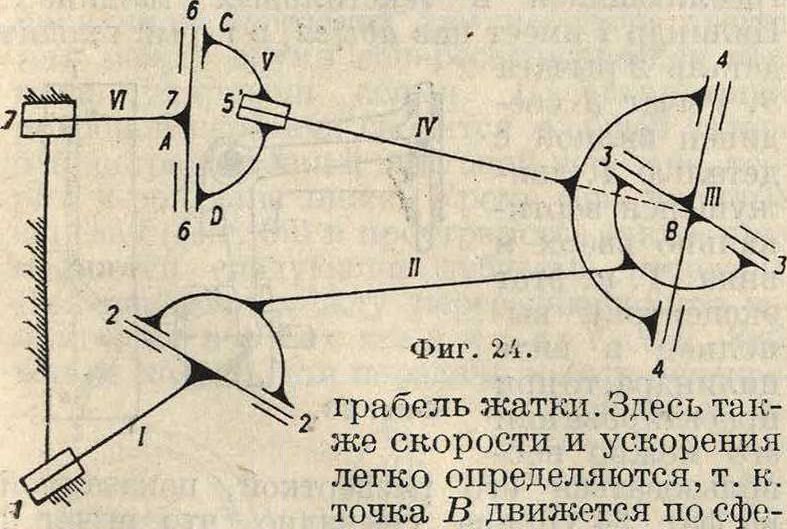
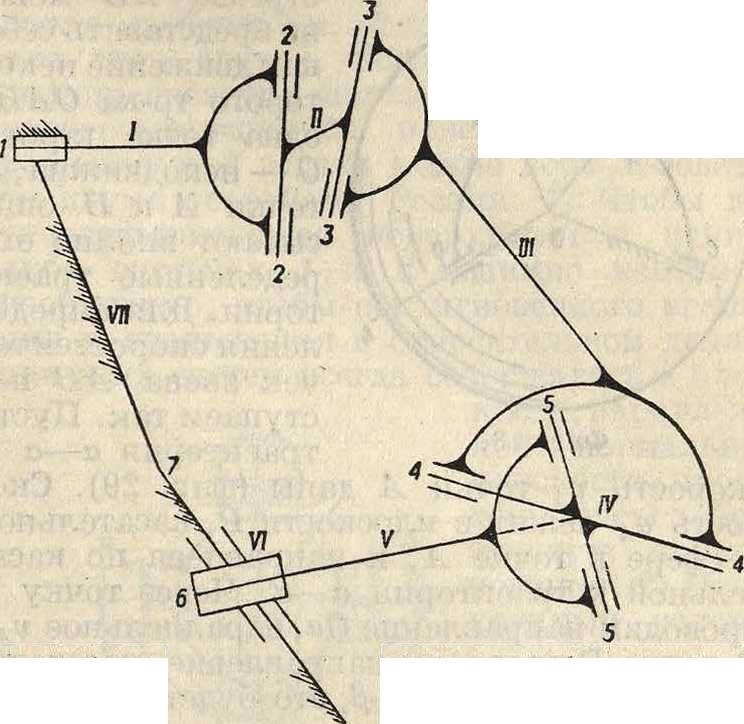
ре радиуса АВ, а точки С и D по окружностям, перпендикулярным к оси 7—7, и следовательно здесь применима теорема о проекциях. На фигуре 25 указан механизм картофелекопателя, легко кинематически исследуемый. Необходимо указать, что при конструктивном выполнении механизмов часто допускают в системе лишние звенья, к-рыми соединяют точки с постоянным между собой расстоянием, наир, в механизме фигура 24 соединяют точки А и В и тому подобное.

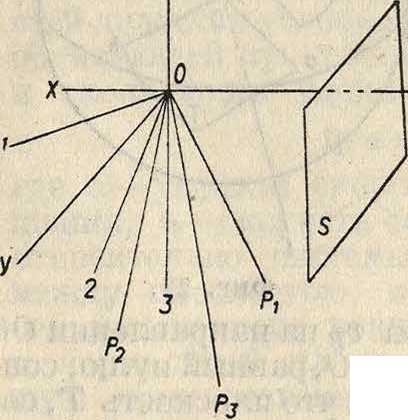
Кроме семиосных механизмов в частном случае в пространстве м. б. шестиосный механизм, но в этом случае он имеет 2 пересечения осей по три. Пусть в точке О пересе каются оси 1, 2 и 3, а в точке О_г—оси 4,

5 и б (фигура 26). Вращение около осей 4, 5 и

6 метров б. заменено вращением около некоторой оси Р, а вращение около оси Р в свою очередь м. б. заменено вращением около параллельной ей оси Р_г, проходя-

Фигура 25.

щей через точку О, и поступательным перемещением в плоскости S, перпендикулярной к ОО_г. Складывая также вращения около осей 1, 2 и 3 и получая ось Р₂, можно далее сложить, вращение Р, и Р₂ и получить вращение около оси Р₃. Т. о. движение какого-либо звена N есть вращение около оси Р₃ и

к

Фигура 26.

скольжение в плоскости S. Вращение дает три компоненты около трех взаимно перпендикулярных осей X, У, Z, а скольжение в плоскости S дает две компоненты, то есть движение звена характеризуется пятью условиями, и следовательно по предыдущему имеем: и—1=5, откуда п= 6, то есть получаем механизм, имеющий шесть звеньев или шесть осей. Схема этого механизма (фигура 27) упо

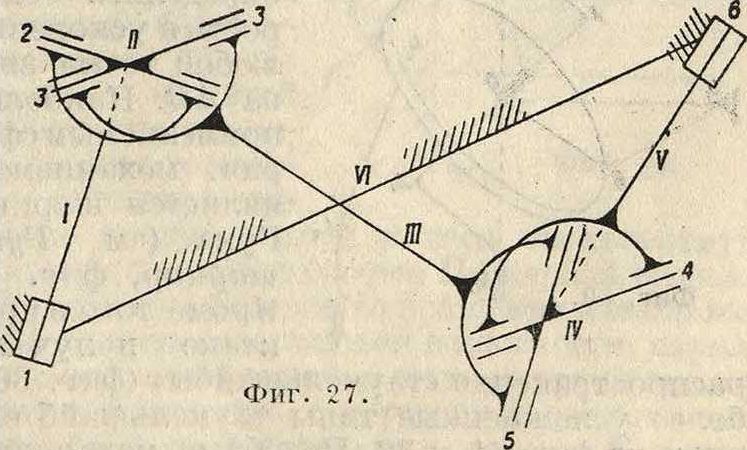
требляется в т. н. двойном шарнире Гука (смотрите Гука шарнир).

Кроме шестизвенного механизма в частном случае м. б. и четырехзвенные механизмы. Наибольшее применение в технике

11

Т. Э. τη. XVIII.

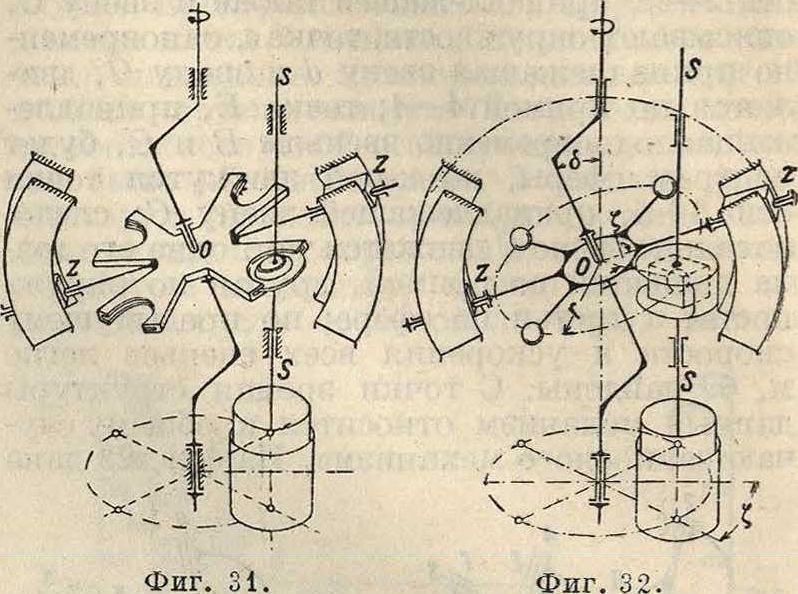
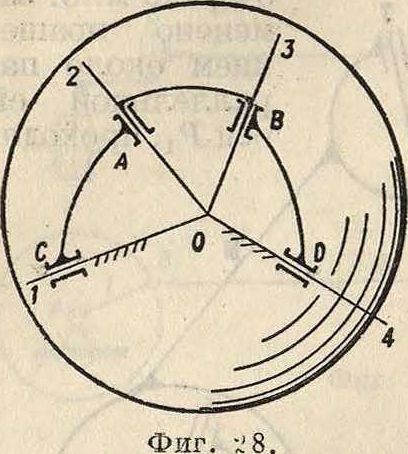
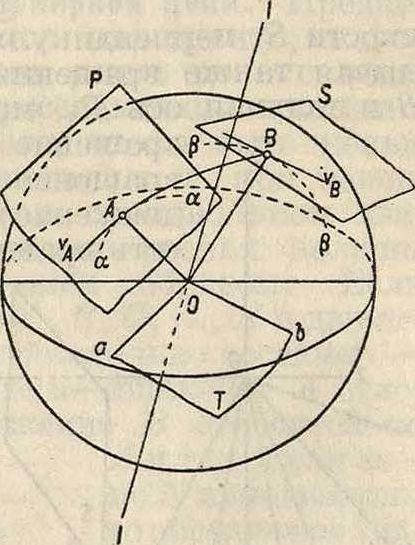
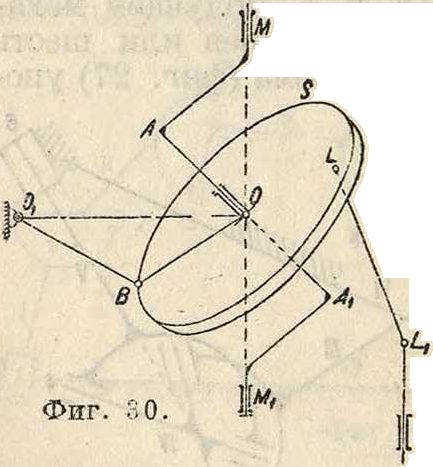
получили т. н. с ф е р и ч е с к и е механизм ы. Сферический четырехзвенный механизм (фигура 28) имеет оси сходящимися в одной точке—центре сферы. Тогда движение отрезка АВ можно представить себе как движение некоторого тр-ка ОАВ, одна точка которого О — неподвижна, а точки А и В описывают вполне ог-ределенные траектории. Для определения скоростейточек звена АВ поступаем так. Пусть траектория а—а и скорость v_A точки А даны (фигура 29). Скорость υ_Α лежит в плоскости Р, касательной к сфере в точке А, и направлена по касательной к траектории а—а. Через точку О проводим направление Оа, параллельное ν_Α. В точке В проводим направление, касательное к траектории β—β, это будет направление скорости точки В. Проводим через точку О направление ОЬ, параллельное υ_Β. Г. к. ось мгновенного вращения и скольжения перпендикулярна к плоскости, содержащей концы векторов скоростей трех точек твердого тела, то принимая точку О за начало плана скоростей и имея, что конец вектора ν_Α должен лежать на направлении Оа, конец вектора υ_Β на направлении ОЬ и вектор скороститочки О, равный нулю, совпадает с точкой О, то есть что плоскость Т, содержащая направления Оа и ОЬ, и будет основной плоскостью плана скоростей, восстанавливаем в точке О перпендикуляр к плоскости Т. Он и будет служить осью мгновенного вращения. Имея ось мгновенного вращения, нетрудно по предыдущему определить скорость и ускорение любой точки звена АВ. Наиболее применяс мым сфе-рич. механизмом является шаргир Гука (смотрите Гука шарнир, фигура ). Кроме того в практике получ ли распространение «таумелыпайбы» (фигура 30); более усложненные типы та.умельшайб смотрите ниже на фигуре 31 и 32. Подобные механизмы нашли себе применение в моторах, изготовленных нек-рыми фирмами. Исследование этих механизмов м. б. произведено вышеуказанными методами. Как показали последние исследования, синтез сферич. механиз мов можно чрезвычайно упростить, пользуясь их аналогия“^ с плоскими механизмами. Необходимо также упомянуть, что кроме сферич. четырехзвенных механизмов м. б. построены и несферич. четырехзвенные механизмы, но при условии соблюдения некоторых геометрических соотношений. Так, для

четырехзвенных механизмов необходимо, чтобы было равенство противоположных звеньев и равенство углов между их осями, и кроме того длины звеньев должны относиться как синусы углов между осями тех же звеньев. Здесь надо отметить, что эти исключения не следует смешивать с механизмами, имеющими также 4 звена (например механизм, указанный на фигуре 18) и работающими за счет свободы в соединениях; структура этих механизмов совершенно неправильна.

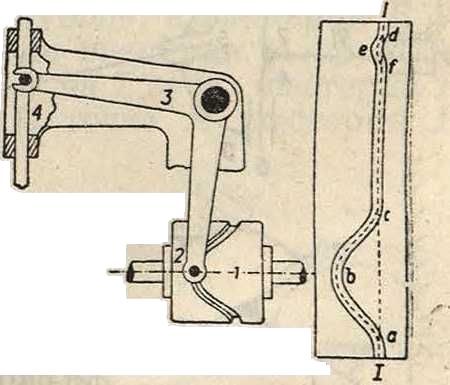
Передачи непосредственным соприкосновением. К передачам непосредственным соприкосновением относятся пространственные кулаки и эксцентрики, а т. кже зубчатые пространственные передачи. На фигуре 33 показан пространственный эксцентрик, употребляющийся в текстильных машинах. Цилиндр 1 имеет паз abefed, в к-рый входит деталь 2 рычага -

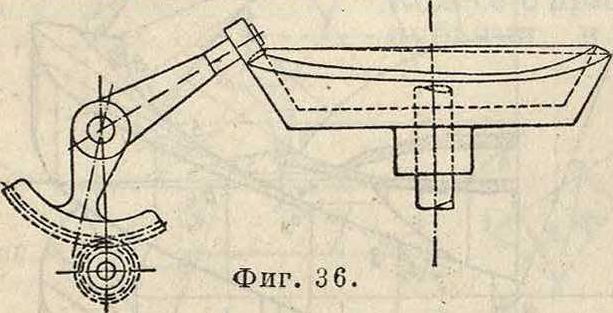
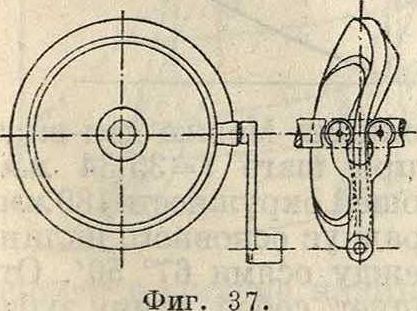
3. Рычаг 3 соединен вилкой с деталью 4, движущейся вертикально вверх и вниз. Т. к. этот эксцентрик выполнен в виде цилиндра, то при проектировании ^фиг· ³³ его можно воспользоваться его разверткой," показанной на фигуре 34 справа. Очевидно, что рычаг 3 получит нужное движение, если развертку протягивать со скоростью, равной линейной скорости точек поверхности цилиндра. Тогда вся задача, будет сведена к обыкновенной плоской задаче, и проектирование эксцентрика сведется к проектированию соответствующей развертки. Скорости и ускорения тогда легко определяются. На фиг". 34 показан эксцентрик, употребляющийся в бумажной промышленности. На фигуре 35 показан эксцентрик жнеи-само-сброски. Ролик п рычага к катится по дорожке s—s. Рычаг к вращается одновременно около оеи У—У, проходящей вертикально через центр главного вала,и горизонтальной оси X—X. На фигуре 36 и 37 даны схемы

Фигура 29.

различных эксцентриков. Т. к. все вышеуказанные эксцентрики развертываются на плоскость, то их проектирование и анализ

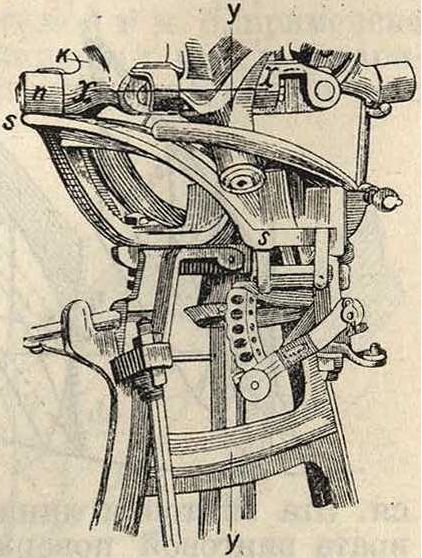
Фигура 35.

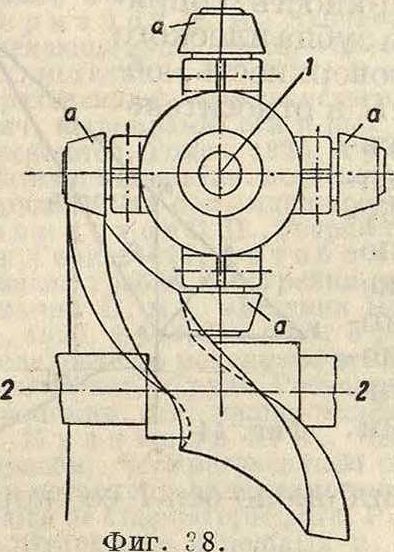
сводятся к случаю, разобранному выше. На фигуре 38 показан шнековый эксцентрик, к-рый занимает промежуточное положение между эксцентриками и зубчатыми передачами. На валу 1 посажена крестовина, оканчивающаяся четырьмя коническими роликами а. На оси 2—.2 имеется винтовая поверхность, находящаяся в каждый данный момент в соприкосновении с двумя роликами. При вращении винтовой поверхности около оси 2—2 крестовина вращается ок. оси 1—1. Означенная передача сходна с

червячной передачей для передачи вращения между двумя непересекающимися перпендикулярными осями. Проектирование подобной передачи сводится к общей задаче о пространственной винтовой передаче, теория которой дана ниже. Кроме фрикционных передач (фигура 39) в пространстве также применяются следующие зубчатые передачи. Для передачи между пересекающимися валами—к онические колеса (смотрите Зубчатые колеса), для передачи между перекрещивающимися валами—в и н т о в ы е колеса и червячная передача и для передачи между непересекающимися и непараллельными осями—г и п е р-болические колеса. Почти все пространственные передачи обладают рядом недостатков.

Приближенное построение профилей приводит к касанию в точках, к большой и неравномерной снашиваемости и к технология. трудностям выполнения. До сих пор вопросу о точном профилировании пространственных колес уделялось мало внимания в практике, хотя и велась теоретич. разработка вопроса (Крайн). Теперь блого

даря работам Н. И. Мерцалова можно практически подойти к решению этой задачи. Ниже дается разработанная проф. Н. Й. Мер— цаловым теория построения поверхностей соприкосновения в пространственных передачах с большим отношением сйоростейс для того случая, когда эти поверхности соприкосновения являются линейчатыми и развертывающимися поверхностями. Для решения этой задачи можно воспользоваться двумя теоремами Резаля. 1) Чтобы две-развертывающиеся поверхности в каких-либо системах 1 я 2 взаимно касались, необходимо, чтобы ось мгновенного вращения и скольжения в относительном движении этих систем всегда содержалась в плос

кости ,параллельной нормальной плоскости, проведенной через образующую прикосновения. 2) Необходимым услови-

т

Фигура 39.

ем касания 2-х развертывающихся поверхностей является условие, чтобы угол а наклона образующей прикосновения к оси вращения и скольжения удовлетворял соотношению

, СО

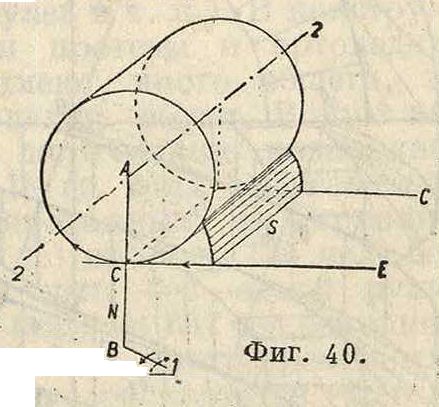
где ω—угловая скорость мгновенного вращения, и—скорость скольжения системы 2 относительно системы 1 и у—расстояние между плоскостью, в которой содержится ось мгновенного вращения и скольжения, и нормальной плоскостью через образующую прикосновения. За одну из поверхностей можно выбрать цилиндрич. поверхность. В случае эвольвентного профиля зубца образование поверхности зубца м. б. представлено (фигура 40) так: цилиндр на оси 2—2 вращается с угловой скоростью колеса, а касательная к нему плоскость Е навертывается на цилиндр без скольжения. Тогда прямая на этой плоскости, параллельная оси колеса, опишет в системе вращающегося колеса эвельвентную цилиндрич. поверхность; По первой теореме Резаля ось мгновенного вращения и скольжения должна содержаться в плоскости, параллельной нормальной, а. в то же время она лежит в плоскости, содержащей направление осей 1 и 2; следовательно плоскость Е, навертывающаяся на цилиндр и содержащая направление оси 2, должна также содержать и направление второй оси 1, и следовательно вторая ось должен быть параллельна плоскости Е. Угол между образующей S и оськрмгно-

*11

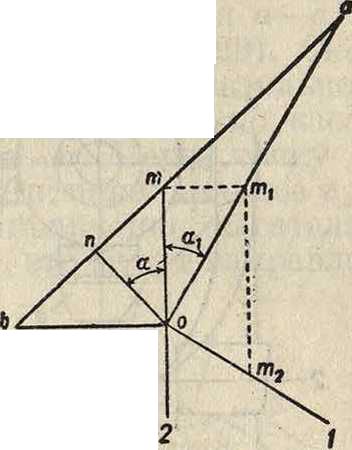
венного вращения и скольжения м. б. найден по второй теореме Резаля—путем построения скоростного пучка (фигура 41), из которого получаем пт V · аb tg α= =

АВОП

откуда или т. к. пт А г>

р=-. Ап,

¹ аЬ

BN Ьп, гукт

— и р Ч- BJS --

AB ab ^г

ВС.

то

ВС

Ьт

Ьа вл.

Тем самым определяется радиус окружности вспомогательного цилиндра. Далее отыскиваем в системе поверхность, сопряженную поверхности зубца плоского колеса. Это будет поверхность, образованная прямой S в относительном движении по системе 1. Это относительное движение будет слагаться из поступательного движения прямой со скоростью точки С вспомогательной окружности в направлении, перпендикулярном к оси 2, и из вращения около оси 1 со скоростью <м,. Из ур-ия:

am. _ АС

аb ~~ АВ

имеем, что скорость точки С выразится отрезком mm, параллельным оb. Скорость же в направлении оси 1 выразится отрезком ощ, точка т₂ которого находится проведением прямой mima, параллельной оси 2. Относительное движение прямой S по системе 1 будет слагаться из движения вдоль оси

Фигура 41.

1 со скоростью о»% и вращения около этой оси со скоростью со,. Подошва кратчайшего расстояния ВС между прямой S и осью 1

опишет при движении прямой £ относительно 1 винтовую линию, а прямая S при своем движении будет этой винтовой линии касать

ся. Эта винтовая линия будет ребром возврата винтовой поверхности, описываемой прямой S. Цилиндрич. колесо будет лежать по одну сторону ребра возврата, то есть крайняя плоскость должна содержать в себе кратчайшее расстояние между осями (фигура 40). Всякое сечение, перпендикулярное к оси винта, дает на винтовой поверхности эвольвенту, в чем нетрудно убедиться из непосредственных построений этих сечений.

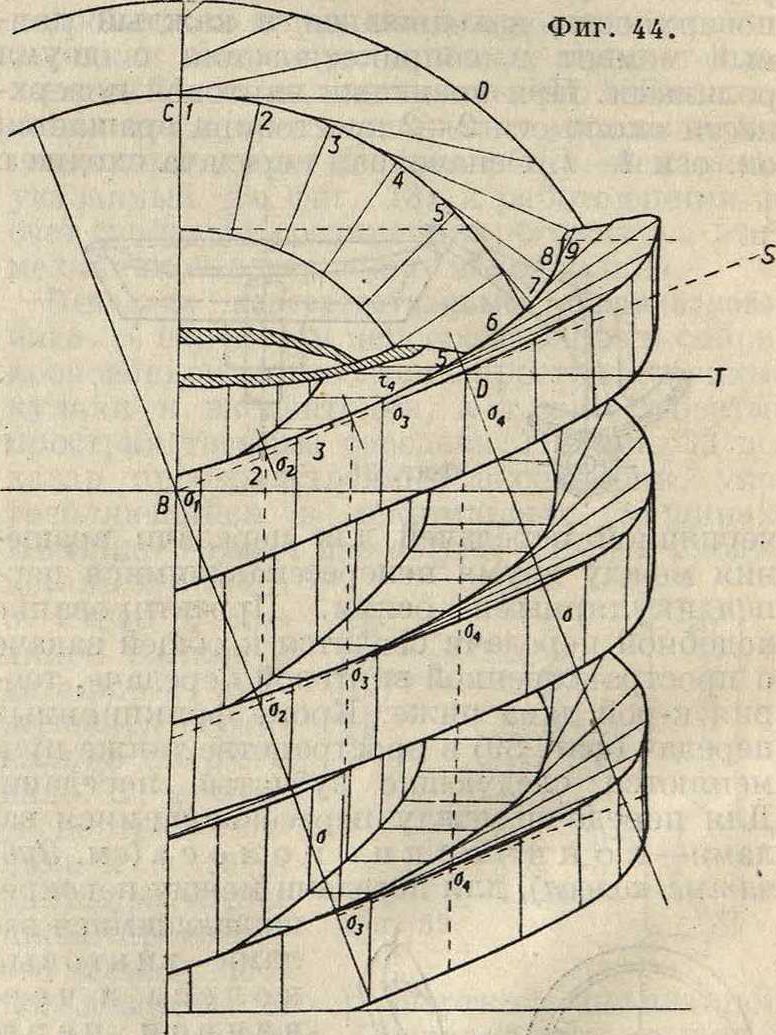
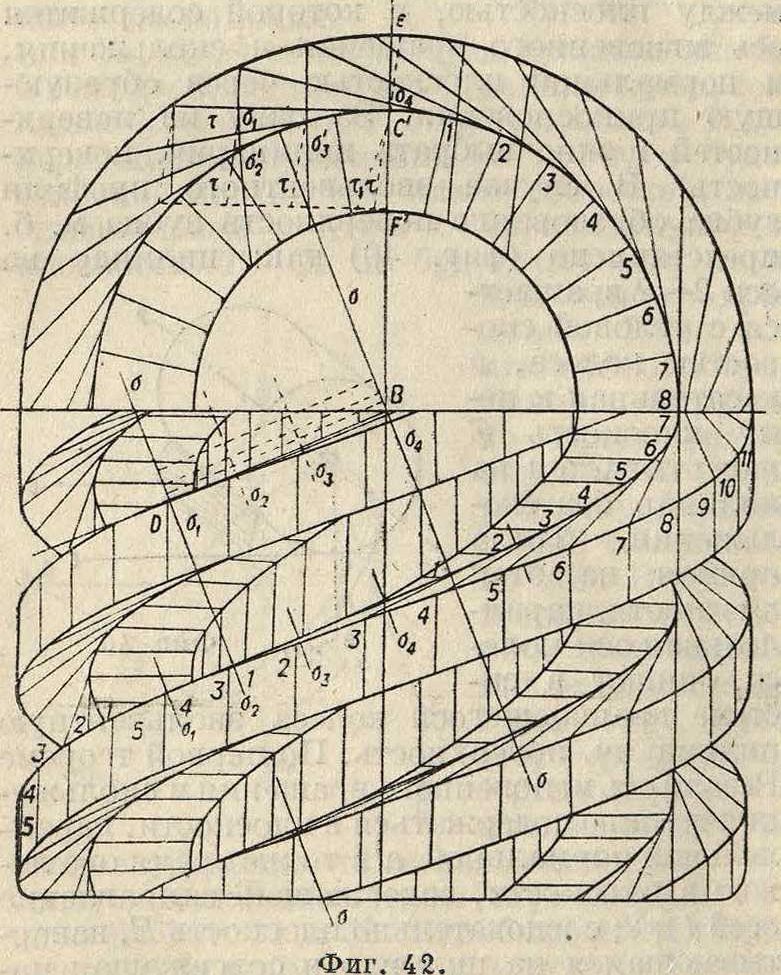
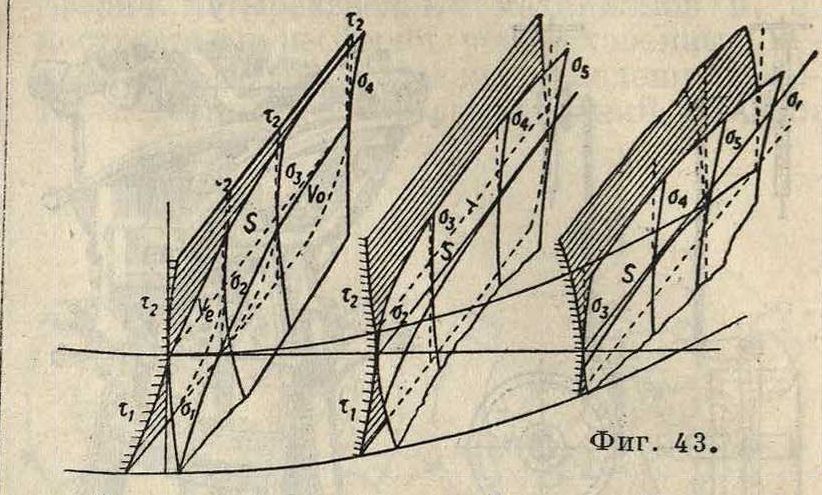
ЗНа фигуре 42 в проекциях Монжа дан винт для передачи 1:8 при шаге t=35,34 миллиметров, при радиусе образующей окружности 180лш. Винт 4-оборотный, радиус основного цилиндра 60 миллиметров. Угол между осями 67° 50. Отрезок BD представляет собой длину зуба, прямая а—σ—ребро возврата. Как уже указывалось, цилиндрич. колесо лежит по одну сторону ребра возврата. Кривые а[, σ₂, ··· и σ, σ₂> ···—проекции эвольвент т, т₂, ., полученных на поверхности зуба сечением, перпендикулярным к оси колеса. На фигуре 43 показаны условия касания трех зубцов в перспективе. Здесь т, т, .—эвольвенты, ап,»,.—кривые сечений винтовых поверхностей, S—линии касания. Поверх-

ность износа этих колес не превышает 6 см². Данная передача между обыкновенным ци-линдрич. колесом с прямыми зубьями и винтом будет необратимой и м. б. применена в грузоподъемных машинах или в сепараторах. В случае расположения колеса не с

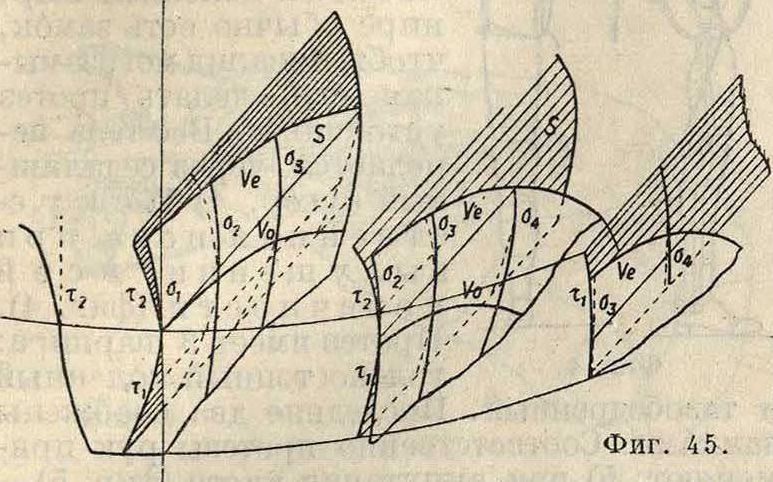
левой стороны (фигура 42), а с правой (фигура 44) соприкосновение будет происходить выпуклой поверхностью по вогнутой. В перспективе это показано на фигуре 45. Нерабочая часть ножки зубца должна быть сильно под-нутрена,.чтобы дать место соответствующему профилю винтовой поверхности.

Передача под прямым углом невозможна при простом цилиндрич. колесе с прямыми зубьями, в этом

Фигура />6.

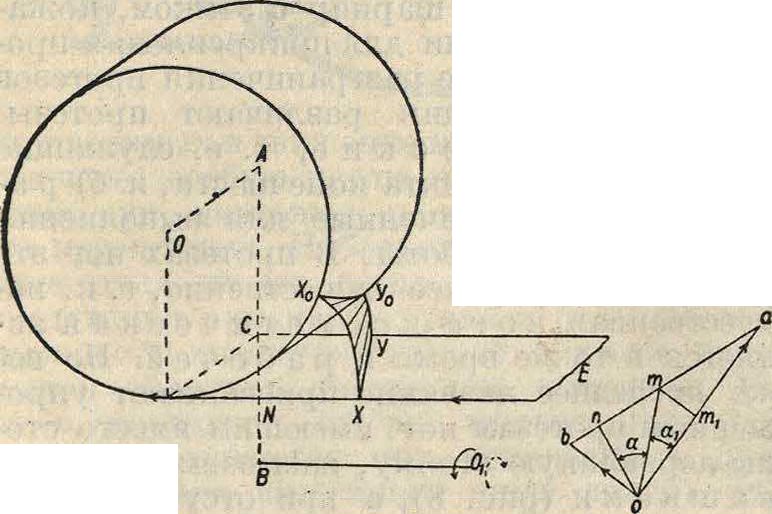
случае зуб колеса должен быть винтовым (фигура 46). Удовлетворяя первой теореме Ре-заля, берем основной цилиндр с радиусом АС и осью АО и проводим к нему касательную плоскость Е. Какая-либо прямая ху на этой плоскости, непараллельная АО,

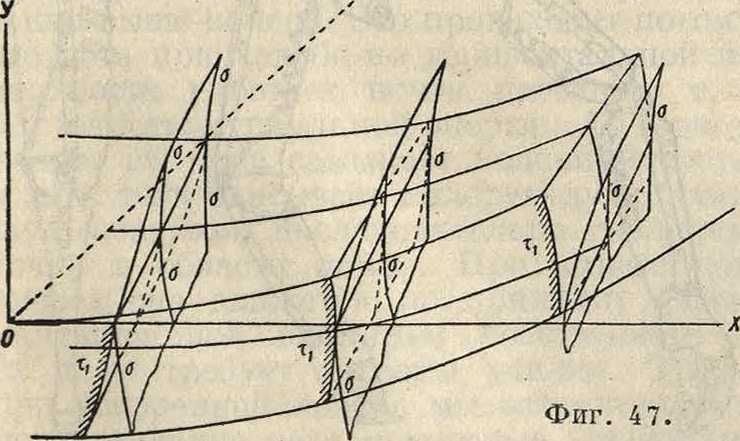
опишет в системе цилиндра при его вращении и наматывании на него плоскости Е линейную эвольвентную поверхность, к которой плоскость Е будет нормальна по образующей ху. Второе соотношение Резаля м. б. найдено из построения скоростного пучка. Построение винта ведется так же, как и для случая непрямоугольной передачи. Колесо располагается по одну сторону от оси винта. Условия соприкосновения даны на фигуре 47. Здесь выпуклая часть зуба работает по выпуклой. В данном случае по существу эта передача является передачей от винта к винту, только колесо будет винтом весьма большого размера и с большим передаточным числом. Передача является необратимой. Подобная же теория дает способы для решения вопроса о касании по линейчатым неразвертывающимся поверхностям.

Передача гибкими тегами в пространстве осуществляется для любого положения осей в пространстве путем применения направляющих шкивов (смотрите Гибкие передачи, Канатная передача). Возможны также передачи при помощи гибких валов (смотрите).

Jlmv.: Артоболевский И., Об ускорении пространственных механизмов, «Сб. тр. Моек. Хи-мико-технологич. ин-та им. Менделеева», М., 1931, вып. 1; Малышев А. II., Анализ и синтез механизмов с точки зрения их структуры, Томск, 1923; Мерцалов Н. И., Зубчатая передача между непе-ресекающимися осями, «Всесоюзный исследоват. ин-т с.-х. мехавики», М., 1932; Верховский А. В. Четырехзвенный пространственный механизм с щлин-дрич. шарнирами, оси которых не параллельны и не пересекаются, Томск, 1925; АртоболевскийИ. И., Синтез и кинематич. исследование сферич.механизмов, «Труды ин-та с.-х. машиностроения», М., 1931; В о с-трокнутовС. П., Теория передачи к ножу в косилках, Горки, 1924; Артоб олевскийС. И., Сбрасывающая грабля лобогрейки (опыт упрощенного исследования П. м.), «Вестник металлопромышленности», М., 1928, 9—10; ГершгоринС. А., К кинематич. исследованию механизма веялок с поперечным движением решет, «Труды Государственного ин-та опытной агрономии, отд. машиноведения», Л., 1929, т. 4, вып. 4; Кузнецов И. Т., Частный случай механизма Горнсби, четырехзвенный сферич. механизм, «Вестник металлопромышленности», М., 1923; R έ s а 1 Н., Traits de kinematique pure, P., 1862; Federhofer

K., Graphische Kinematik u. Kinetostatik des starren raum lichen System es, W., 1928; Thier ing 0., Getriebe d. Textiltechnik, B., 1926; Scbaudt G., Die Schubkurventriebe, Stg., 1927; Muller O., Beschleuningungsverhaltnisse beim spharischen Kur-beltrieb u. verwandten Mechanismen, «Z. d. VDI», 1929, B. 73, 4; R e u 1 e a u x F., Theoretische Kinematik, В. 1, Brschw., 1875; GrashofF., Theoretische Ma-schinenlehre, B. 2, Hamburg, 1883; Crain R.,

S chraub enrader mi t ger ad linigen E ingriff sf la cb en, «W eik-stattstechnik»,B., 19П7, H. 2—3u. ff. И. Артоболевский.