> Техника, страница 74 > Прочность

Прочность

Прочность, способность твердых тел подвергаться в определенных пределах дей-

£

«О

*0

СО Со CQ Со Со

ε ε ε ε

Со <о <6

расст. 1,5м Ι--

2отделЬн. оси

ФФ

ствию внешних сил, не разрушаясь и не получая практически ощутимых остаточных деформаций. П. таким образом харак теризуется теми предельными условиями, которым соответствует или появление первых остаточных деформаций (смотрите Деформация пластическая) или же начало разрушения,

в зависимости от того, какое из этих двух явлений наступит при данных условиях раньше. Весьма часто однако под прочностью понимают только сопротивление раз рушению, а не деформации. Прочность твердых тел является результатом сил сцепления между атомами, составляющими тело. Природа этих сил идентична с природой сил химич. сродства. Однако наблюдаемая в действительности прочность материалов имеет значения во много раз меньшие, чем те, которые следовало бы ожидать, если исходить из теоретически исчисляемых величин междуатомного сцепления, с одной стороны, и величин напряжений, находимых по правилам сопротивления материалов или теории упругости, с другой. Это обстоятельство объясняется в первую очередь тем, что действительное изменение напряженного состояния в деформируемых телах и изменение свойств самого материала тела в значительной мере отлетаются, особенно на границе преодоления П. материала, От той закономерности и постепенности, которая предполагается теорией упругости или строительной механикой. Значения напряжений, получаемые расчетом по методам этих дисциплин, исходящих в своем построении из гипотезы идеальной однородности и упругости тела, должны рассматриваться лишь как некоторые статистич. средние значения действительных напряжений в данном пункте тела. При этом от средних значений возможны весьма большие отклонения или перенапряжения.

Механизм деформации или разрушения, благодаря наличию указанных перенапряжений, заключается в последовательном местном преодолении сил сцепления в наиболее для каждого данного момента времени перенапряженных точках тела. В телах аморфных это нарушение прочности может мыслиться как последовательное преодоление сил· сцеплений между каждыми двумя соседними атомами в отдельности. В отношении моно- или поликристаллич. тел нарушение П. схематически может быть представлено как одновременное массовое на -рушение сил сцепления между атомами, лежащими в двух соседних плоскостях кристаллографии. решетки данного кристалла или кристаллита. Результатом этого нарушения сил сцепления являются сдвиги атомов, лежащих в одной из таких плоскостей, относительно атомов соседней плоскости. При нек-рых условиях нарушение П. в поликрист может произойти и в результате сдвига зерна по зерну. Кроме этих сдвигов для объяснения пластич. деформации кристаллич. тела необходимо допустить и наличие ряда осложняющих явлений (смотрите Деформация пластическая). Кроме деформации или разрушения путем сдвигов или скалываний разрушение может происходить и путем разрыва или расщепления по плоскостям кристаллографии, решетки или по границам зерен. Всякое обстоятельство, увеличивающее неоднородность в распределении напряжений, как то: наличие внешних и внутренних пороков, понижает П. тел, и. наоборот, уменьшение неоднородности в распределении напряжений может значительно повысить П. тела. Есть наир, основание предполагать, что с уменьшением поперечного сечения растягиваемого образца распределение напряжений будет более однородным, соответственно чему следует ожидать и повышение П. Нек-рым подтвержде нием этого предположения могут служить •опыты Гриффита. Этот исследователь, экспериментируя над стеклянными нитями с диам. от 0,04 до 0,00012 дм., получил определенную зависимость между уменьшением диаметра и увеличением врем, сопротивления нити. Экстраполируя эту зависимость до диаметра, равного нулю, Гриффит получил значения временного сопротивления одного порядка с теоретически исчисленной величиной междуатомного сцепления.

Особую роль по гипотезе, выдвинутой тем же Гриффитом, в понижении П. кристалла играет образование на поверхности его микроскопических или субмикроскопических тонких и острых трещин. Перенапряжение на краях таких трещин вызывает их рост, связанный с дальнейшими перенапряжениями, в результате чего имеет место расщепление кристалла уже при сравнительно низком среднем для всего сечения напряжении. Предположение Гриффита было подтверждено рядом опытов. Так, А. Ф. Иоффе, испытывая на растяжение кристаллы каменной соли, погруженные в горячую воду, чем достигалось удаление образующихся поверхностных трещин растворением, фактически получал значения П., определяемые как отношение нагрузки к окончательному •сечению при разрыве, одного порядка с теоретическими величинами междуатомного сцепления в кристалле. В поликристаллич. телах наличие или образование таких понижающих П. трещин следует предполагать в отношении каждого кристаллита, входящего в состав тела, результатом чего и является понижение П. всего тела. Согласно предположению Смекала пониженная П. против теоретически исчисляемых величин может быть объяснена также тем, что в реальных крист вероятно имеются выпадения определенных групп атомов из кристал-.лографич. решетки кристалла. Эти выпадения создают пустоты, являющиеся источниками концентрации напряжений. Такие явления, как фотоэлектрич. эффект и флуоресценция, косвенно подтверждают предположения Смекала. В значительной мере П. тел зависит от величины внутренних напряжений, то есть от напряжений, имеющих ме-сто в теле при отсутствии внешних сил и взаимно уравновешивающихся, или в пределах значительной части объёма тела, наир, по всему поперечному сечению, или же в пределах весьма малых, даже микроскопии, или субмикроскопических зон.

П. аморфных тел в большей степени, чем П. тел кристаллических зависит от длительности приложения нагрузки. Например такое аморфное тело, как вар, находясь под длительным действием сил тяжести, может вытечь сквозь тонкое отверстие сосуда, в к-ром он помещен. Между тем тот же вар обладает сравнительно высоким сопротивлением в -случае,быстрого приложения нагрузки. Влияние на П. изменений ί° в отношении материала в аморфном состоянии как правило является также значительно большим, чем в отношении того яге материала в состоянии кристаллическом. При определенной ί° кри-сталлич. и аморфное состояния являются равнопрочными. Выше этой ί° ббльшую П. дает состояние кристаллическое, ниже этой темп-ры—аморфное. В отношении тел поли кристаллических широкое распространение имеет гипотеза об аморфном или полуаморф-ном состоянии вещества на границах отдельных кристаллов, составляющих тело. Гипотеза эта удовлетворительно объясняет, в связи с разным влиянием t° на П. тел аморфных и кристаллических, тот факт, что как правило у металлов деформация происходит при низких ί° путем сдвигов внутри зерна, а при высоких—путем сдвигов зерна по зерну. В отношении тел кристаллических как правило изменение темп-ры в большей степени отражается на пределе упругости, то есть на величине напряжений, при которых появляются первые сдвиги, чем на величине напряжений, соответствующих моменту разрыва. Ниже определенной t° разрыв происходит до достижения предела упругости, и тело рвется без деформации; выше этой ί° сначала имеет место достижение предела упругости, материал пластически деформируется и затем лишь разрывается. Т. о. в зависимости от t° одно и то же тело может быть и хрупким и пластичным и прочность его в зависимости от условий может определяться как появлением остаточных деформаций, так и разрушением без деформаций.

П. монокристаллич. тел в весьма значительной степени зависит от ориентировки кристаллографических осей тела по отношению к действующим усилиям и является функцией этой ориентировки. При совпадении плоскостей наименьшего сопротивления сдвигу с направлением наибольших тангенциальных напряжений остаточные деформации в кристалле имеют место уже при очень низких значениях действующих сил. По предположениям нек-рых исследователей (Бриджмен и др.) сдвиги в свободном от внутренних напряжений кристалле идеально химически чистого металла должны начинаться при всяком напряжении, отличном от нуля. Такой кристалл по своим свойствам напоминал бы жидкость, атомы которой имели бы лишь строго определенное относительное расположение, обусловленное характером данной кристаллографии, решетки. Наличие в кристаллографической решетке атомов двух разных элементов, затрудняя процесс сдвига, повышает прочность кристаллов. Поэтому П. тела, представляющего твердый раствор одного компонента в другом, всегда выше той, которая имела бы место в том случае, если бы П. подчинялась закону аддитивности свойств компонентов. Нарушение П. путем сдвигов у монокристаллов всегда происходит по сравнительно небольшому, по сравнению с общим, числу плоскостей. Остается еще далеко невыясненным, какие обстоятельства делают эти плоскости плоскостями меньшего сопротивления, чем соседние с ними. Возможно, что здесь играют роль трещины Гриффита или пустоты Смекала. После того как сдвиг по данной плоскости или системе смежных плоскостей достигнет некоторой величины, сдвиг по этим плоскостям прекращается, и сопротивление сдвигу в них делается большим, чем по недеформированным плоскостям. При дальнейшем возрастании нагрузки явление сдвига должно происходить по новым плоскостям со все большим сопротивлением, и требуется все нарастаю щее напряжение, чтобы нарушить П. Явление это называется упрочнением. В результате такого упрочнения П., например кристаллов каменной соли, может возрасти до 12 раз. Природа явлений, обусловливающих упрочнение по той плоскости, по которой начался сдвиг, а равно и общее упрочнение тела, во многом остается еще невыясненной. Ряд выдвинутых для объяснения упрочнения гипотез, как то:предположение об образовании по плоскостям скольжения аморфных прослоек, искажений кристаллография, решетки и возникновения больших внутренних натяжений и т. д., не в состоянии объяснить столь большого упрочнения, как это было например указано для случая каменной соли.

При определенной ориентировке кристалла нарушение П. может произойти и путем разрыва, а не сдвига. Это будет иметь место в том случае, когда кристалл ориентирован так, что нарушение сопротивления разрыву будет превзойдено раньше, чем тангенциальные напряжения в плоскостях, по которым возможен сдвиг, превзойдут сопротивление сдвигу. Так. обр. при одной и той же t° один и тот же кристалл может под нагрузкой, в зависимости от ориентации, вести себя и как пластичное и как хрупкое тело. В телах поликристаллических П. обусловливается не только сопротивлением сдвигу по кристаллографии. плоскостям отдельных кристаллитов, но и сопротивлением сдвигам на границах зерен. Последнее сопротивление объясняется, с одной стороны, различной ориентировкой плоскостей наименьшего сопротивления сдвигу у разных кристаллитов, а с другой,—большей П. вещества в разделяющем два соседних кристаллита слое. Подобно тому как это имеет место в отношении монокристалла, и в поликристалле сдвиги затрагивают в каждом кристаллите сравнительно немного плоскостей или систем смежных плоскостей. Упрочнение, имеющее место и в отношении тел поликристаллических, здесь повидимому объясняется главным образом возрастанием сопротивления сдвигу на границах зерен. П. поликриеталлич. чистых металлов как правило меньше, чем П. твердых растворов, по той же причине, как это указывалось выше в отношении монокристаллов. При уменьшении размеров зерен П. возрастает, ибо параллельно с уменьшением размера зерен и следовательно с увеличением их числа возрастает роль сопротивлений сдвигу на границах зерен. При наличии зерен двух различных типов роль сопротивления сдвигу в результате взаимодействия соседних зерен может еще больше возрасти. В таком агрегатном состоянии наличие более твердой составляющей даже в незначительном проценте может повести к значительному повышению прочности.

Холодная обработка вследствие вызываемого ей упрочнения может значительно повысить П. материала. Однако весьма интенсивная холодная обработка, доведенная до возникновения местных разрушений, может П. материала понизить. Холодная деформация одного знака также как правило понижает П., в частности предел упругости, в отношении напряжений обратного знака. Напр. растяжение, связанное с появлением остаточных деформаций, повышает предел упругости в случае вторичного растяжения, но понижает предел упругости для случая последующего сжатия. Горячая и холодная обработка значительно изменяет П. тела, создавая преимущественную ориентировку кристаллитов тела. Поэтому прочность прокатанных металлов в направлении вдоль прокатки выше, а в направлении поперек прокатки ниже, чем для необработанного металла. Весьма значительное влияние на П. металлов имеет и термическая обработка. В отношении таких тел, как искусственные и естественные камни, на прочность имеют большое влияние не только механич. свойства агрегатов, входящих в состав тела, но и степень сцепления между отдельными составляющими и степень пористости. Увеличением например пористости в значительной мере объясняют понижение прочности бетонов, если при изготовлении их применялся избыток воды против количества, необходимого для завершения химия, процесса твердения раствора. Для тел гигроскопичных, (древесина, ткани и т. д.) особое влияние на П. имеет степень их влажности.

Многообразие причин, обусловливающих П. тел и нарушение этой П., многочисленные аномалии, сопровождающие деформацию и разрушение, как то: упругое последействие, усталость, упругий гистерезис, наличие внутренних напряжений, пороков и тому подобное. обстоятельства, крайне затрудняют создание достаточно простых и вместе с тем общих теорий, одинаково объясняющих прочность тел из различных материалов и в различных случаях напряженного состояния. Строгое рассмотрение результатов эксперимента и наблюдения над работой материала в лабораторных образцах и в действительных сооружениях приводит многих исследователей к мысли о невозможности создания в этой области каких-либо общих теорий и о необходимости каждый частный случай рассматривать и описывать как чисто индивидуальное явление. Несмотря на всю вескость доводов этих исследователей, отвечая потребности практики в методах аналитич. оценки П. и общему стремлению науки объяснять возможно больший круг явлений одного порядка, исходя из возможно меньшего числа основных положений, был создан целый ряд т.н. теорийП. Если эти теории и не в состоянии вместить любой частный случай деформации и разрушения, то все же многие из них дают возможность объяснить и предвидеть значение П. в достаточно широких пределах. Теперешний уровень наших знаний не позволяет построить теорию прочности, основанную на рассмотрении действительного строения твердых тел и действительной природы явлений деформации и разрушения. Современная элек-трич. теория кристаллов разрешает вопрос П. только в отношении кристаллов с простейшего типа решеткой и только в отношении частных случаев напряженного состояния; использовать выводы этой теории для расчетной практики пока не представляется возможным. Поэтому в построении теории П. приходится исходить из чисто формальных предположений, выбираемых т. о., чтобы на основе их можно было обнять все или возможно большее число частных елу-

чаев, уже известных из опыта или эксперимента. Поэтому вновь обнаруживаемые свойства и факты очень часто не укладываются в рамки старых теорий и для объяснения этих фактов приходится старые теории видоизменять или заменять другими.

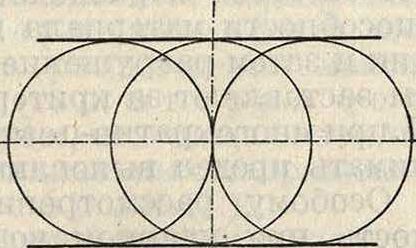
Наиболее ранней из всех теорий П. является теория, основанная на предположении, что пределы П. обусловливаются определенным для данного материала максимальным значением нормального напряжения, при превышении которого начинается деформация или разрушение. Теория эта впервые была выдвинута Галли-леем, затем Лейбницем, Ранкином и др. Согласно этой теории П. определяется только наибольшим по абсолютной величине главным напряжением, и следовательно предельное значение нормальных напряжений для любого случая напряженного состояния то же самое, что и для случая чистого одностороннего растяжения или сжатия. Справедливость этой теории опровергается экспериментом, в частности опытами по всестороннему гидростатич. сжатию. Действительно в случае такого сжатия, при отсутствии пор, тела не деформируются и не разрушаются при сколь* угодно большом значении сжимающих напряжений. Расчеты П. на основе этой теории, за исключением случаев чистого растяжения и сжатия, приводят к неправильным выводам. Второй теорией П. была теория, выдвинутая Мариот-том, Сен-Венаном, Грасгофом, Бахом и по недоразумению довольно широко применяемая и до настоящего времени. Согласно этой теории П. обусловливается некоторой постоянной для данного материала предельной величиной положительного удлинения. Теория эта совершенно не оправдывается опытом. В частности согласно этой теории для металлов, у которых число Пуассона, как известно, колеблется между 7з и */₄, предел упругости при сжатии должен был бы быть в 3—4 раза выше, чем при растяжении, что совершенно противоречит действительности. Для расчетов П. и эта. вторая теория должна считаться неприемлемой. Попытки внести корректив в эту теорию путем предположения, что кроме предельного значения положительного удлинения существует и предельное значение удлинения отрицательного, также оказались безуспешными. С таким коррективом теория Сен-Венана—Ма-риотта не может быть увязана с результатами опытов по всестороннему сжатию. Уже в 1773 г. Кулоном была выдвинута третья гипотеза прочности, заключавшаяся в предположении, что нарушения сил сцепления не происходит, пока нигде и ни в каком направлении величина тангенциального напряжения г не превышает значения τ₀+νσ, где величина т₀ есть некоторая постоянная для данного материала, зависящая от силы сцепления, ν—коэф. внутреннего трения и σ—нормальное напряжение к данной площадке. Теория Кулона учитывает т. о. сопротивление сдвигу в результате как сил сцепления, так и внутреннего трения. Для литой стали коэф. внутреннего трения может быть принят равным нулю. В этом случае условие П. должно определяться предельным значением т_тах, максимального тангенциального напряжения. Т. к. максимальное значение тангенциального напряжения выражается через разность между наибольшим и наименьшим из главных нормальных напряжений, то в отношении тел, для которых ν=0, прочность тела согласно теории Кулона может определяться некоторым постоянным для данного материала предельным значением разности главных напряжений в_х и а_г, где а_х > а_у >сг_г. В такой форме эта теория П. была впервые сформулирована Треска. Весьма часто эту теорию называют английской [по Гесту (Guest)—maximum difference stress theory]. В более общей форме теория П., исходящая из рассмотрения величины тангенциальных напряжений, была развита Отто Мором, который положил в ее основу разработанный им же метод графического изображения напряженного состоянияте-л а (смотрите Напряженное состояние). Согласно предположению Мора прочность каждого· материала определяется некоторым предельным значением тангенциального напряжения, являющимся в свою очередь функцией величины нормального напряжения к данной площадке. При этом согласно теории Мора среднее по величине из главных нормальных напряжений а_у не играет роли в нарушении П., и последняя зависит только от значений двух крайних по величине главных напряжений а_х и а_г. Это допущение равносильно предположению, что остаточная деформация или разрушение в Данной точке может происходить путем сдвигов только по таким плоскостям, в которых лежит средняя по величине главная ось эллипсоида напряжений. Благодаря таким предположениям, предельное значение тангенциального напряжения, определяющее прочность тела для любого пространственного случая напряженного состояния, может быть по Отто Мору представлено некоторой кривой в плоской системе координат. Из трех кругов, необходимых для изображения по методу Мора напряженного состояния; рассмотрению при суждении о прочности подлежит, вследствие указанных выше предпосылок, только внешний, то есть наибольший круг. Каждому частному случаю, определяемому известным соотношением крайних значений главных напряжений σ_χ и а, должно соответствовать свое предельное значение тангенциального напряжения, переход за к-рое вызывает нарушение П. Следовательно различным частным случаям предельного, то есть находящегося на границе П., состояния будут соответствовать разные диаметры внешних кругов Мора. Огибающая семейства таких кругов, построенных при сохранении одного начала координат для различных случаев предельного состояния, и будет представлять собою кривую, определяющую предельное для П. значение тангенциального напряжения в ф-ии нормального напряжения к соответствующей площадке. Для построения этой кривой могут быть использованы результаты эксперимента для различных частных случаев, например для случаев чистого растяжения (а_у=σ_ζ=О, σ_χ >0),*чистого сжатия (<*_х=а_у=0, σ_ζ<0), чистого сдвига (σ_χ=- <“, в_у=<7 и т. д. (фигура 1). Теория Кулона представляет собой частный случай теории Мора, именно тот, когда огибающие кривые Мора превращаются в две прямые (фигура 2). Теория Кулона в отношении тел, для которых коэф-т внутреннего трения равен нулю, представляет собой тот частный случай, когда эти огибаю

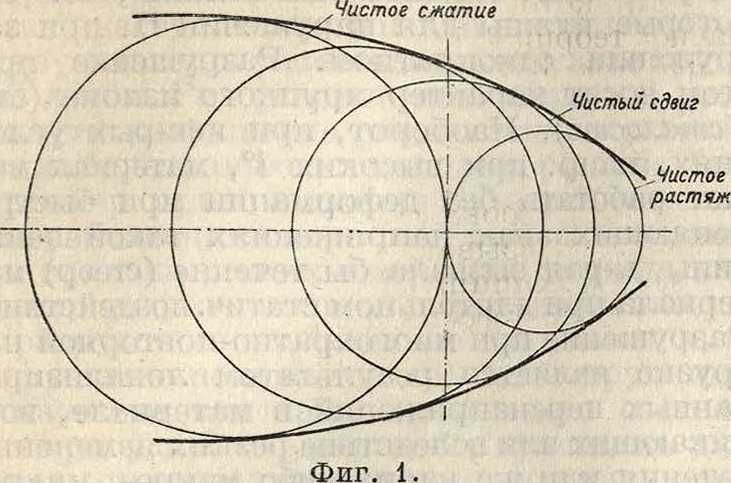
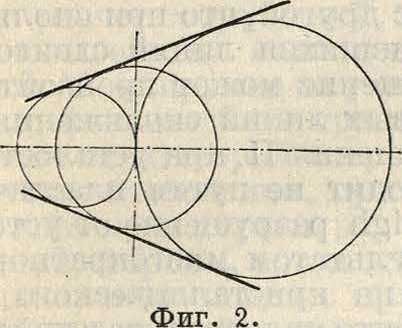
щие кривые превращаются в две параллельные прямые (фигура 3).

Проведенные с большой точностью эксперименты Бекера (Beckker) в 1915 году и Л оде (Lode) в 1926 году показали, что среднее из главных напряжений имеет все же нек-рое, хотя незначительное, влияние на 1Ί. тел и что следовательно теория Мора не вполне точна. Принципиально пользуясь теорией прочности Мора, можно за предельное состояние принимать пределы упругости, равно как и пропорциональности, и текучести, а также и П. при разрыве, определяя ординаты огибающей кривой (Grenzkur-ve) по соответствующим этим пределам данным эксперимента. В частной своей форме, именно для значения коэф. v, равного нулю, теория Мора дает достаточно точные решения для таких металлов, как сталь и медь. В своей общей форме теория Мора дает результаты, удовлетворительно совпадающие с данными эксперимента в отношении таких хрупких ма- Фигура з. териалов, как бетон, мрамор, песчаник и т. д., для тех случаев, когда разрушение этих материалов происходит путем скалывания. Случаи разрушения тел путем хрупкого разрыва (Zerreissungsbruch, Tren-nungsbrueh) выходят за пределы применимости теории Мора. Недостатком теории Мора являются значительные затруднения математич. порядка при ее применении для сложных случаев пространственного напряженного состояния. Рядом авторов были сделаны попытки внести частичные коррективы в вышеприведенные теории П. Так, Бекер указывал, что наиболее справедливым решением будет сочетание первой и третьей теории прочности. Рейто (Reyto) для объяснения того факта, что линии Пио-бера-Людерса-Гартмана имеют разный наклон для случаев сжатия и растяжения, считает необходимым и для мягкой стали учитывать внутреннее трение. Эти поправки

не вошли в виду своей сложности и неопределенности в расчетную практику. В 1885 году итальянский математик Белтрами выдвинул предположение, что остающееся деформирование материала начинается тогда, когда для данного элемента объёма тела будет превзойдено некоторое зависящее от свойств материала предельное значепие энергии упругой деформации. В такой простейшей форме теория Белтрами не может быть увязана с результатами опытов по всестороннему сжатию, так как энергия упругой деформации на единицу объёма тела может в таком случае быть доведенной до любой величины без того, чтобы в-теле появилась остаточная деформация. Так. обр. и теория Белтрами должна признаваться в качестве общей теории неприемлемой. Однако в дальнейшем эта теория была значительно развита и в нынешней ее формулировке теория прочности, основанная на рассмотрении предельного значения энергии деформации, ближе всего отвечает результатам опытов в отношении пластичных металлов.

Для отнесенной к единице объёма энергии или работы деформации А можно дать следующее выражение:

А=+ ^σν + ^σζ) (в_хв_у + σ_χσ_ζ + а_ув_а) +

“Ь 2 О (^τΗ “Ь ^τχζ "Ь ^Tijz) >

или через деформации А=G { 4 + 4 + ^ε1 + Τ^Γμ +

+ I (vly + Y%z + Vyz) } ’

где о—нормальные напряжения, т—касательные напряжения, ε—линейные деформации растяжения или сжатия, а γ—деформация сдвига.

Выбор значения А в качестве критерия для определения предельного для прочности состояния является принципиально весьма удачным. Действительно, в выражение для А (смотрите выше) входят все три нормальные и Есе три тангенциальные напряжения, а также константы, характеризующие свойства материала, именно модули упругости Б, G и коэф. Пуассона μ. Если условно приравнять величину А значению то тогда а_е=]/2 ЕА может рассматриваться как нек-рое приведенное напряжение, величина которого для случая чистого растяжения или сжатия дала бы то же значение энергии деформации, как и данное сочетание напряжений; По предельному значению а_е, полученному экспериментом для случая растяжения, можно следовательно определить и предельное напряженное состояние для любого частного случая. По теории, выдвинутой М. Huber’ом (1908) и затем Henky, следует величину энергии деформации расчленить на две величины, именно на величину энергии А_д, идущей на изменение формы, и величину энергии А_р, идущей на изменение плотности, причем А=А_р + А_д. Согласно теории упругости

А=^{1 + μ}

Р 3 (1 — 2 μ)

где объёмная деформация

6 ε_χ -f- By -j- ε₃

₌ 3 (1 — 2 /t)

E V’

а среднее гидростатическое сжатие

Р= 1 (^ах + °у + ^σζ)

И

Л=IFg {(^σ* - ^σ2/)² + О* - <Κ)² + К - ^σ*)²} +

+ ^ {^τΙ_ν + ^τχζ + ^τ1ζ)

Если е, а следовательно и р больше нуля, то характеризующим П. по теории Huber’a является полное значение А, если же е < О и р < 0, то критерием П. является только значение А_д и за приведенное напряжение а_е следует принимать значение а_е=γ2ΕΑ~_ν.

Опыты Karmen’а и Геста показали, что теория Huber’a тоже не дает безусловного совпадения с данными эксперимента. Согласно Л оде (1926 год) зависимость между началом пластической деформации и энергией деформации м. б. сформулирована след. обр.: «для момента наступления текучести материала значение А_д является величиной постоянной». Mises и Schleicher (1925 год) предложили в качестве кривой, характеризующей предельное для П. состояние, такую кривую, у которой абсциссе х=р=| (<у_х + а_у + + σ_ζ) соответствует значение ординаты у== а_е=]/2ЁА, определяемое подобно тому, как и для кривой Мора, опытом. Если у будет больше ]/2 ЕА при определенном значении р, то в теле должны иметь место неупругие деформации, то есть нарушение П. Дальнейшее развитие и экспериментальное обоснование теорий П., основанных на рассмотрении энергии деформации, дали Ros и Eichinger.

В основе всех вышеизложенных теорий лежит предположение об однородности и непрерывности тела. Общим для всех них является также допущение, что распределение напряжений в предельном состоянии подчиняется тем же законам, как и при упругой деформации. Благодаря таким предположениям, эти теории неприменимы или применимы лишь в качестве некоторого приближения для тел а н и з о-тройных (например монокристаллы) или гетеротропных (например прокатный металл, железобетон и т. д.). Эти теории не могут быть увязаны и с особенностями микроструктуры, хотя эти особенности в значительной мере определяют П. материала. Mesnager сделал интересную попытку распространить теорию П. на тела из материала, хотя и однородного, но не непрерывного, именно содержащего редкие еферич. пустоты. На основании своих рассуждений Mesnager приходит к заключению, что условие П. нельзя выразить одной кривой, как это предлагает Мор, а необходимо ввести в рассмотрение для каждого материала две кривые, определяющие предельное состояние: одну в отношении хрупкого разрушения, другую в отношении пластин, деформации. Это предположение находит свое подтверждение в опытах Karman’a, к-рый показал, что материалы, обычно хрупкие, могут пластически деформироваться при известных сочетаниях напряжений а_х, а_у и σ_ζ.

Все приведенные теории относятся к случаю статической нагрузки. В случае многократно прилагаемой (пульсирующей) на грузки, особенно знакопеременной, условия П. и механизм разрушения коренным образом меняются. Тело может разрушиться при многократно-повторном загружении при напряжениях значительно низших, чем те, которые нужны для нарушения П. при загружении однократном. Разрушение при этом носит характер хрупкого излома (смотрите Усталость). Наоборот, при нек-рых условиях, наир, при высоких ί°, материал может работать без деформации при быстро меняющих знак напряжениях такой величины, которая вызвала бы течение (creep) материала при длительном статич. воздействии. Разрушение при многократно-повторной нагрузке является результатом локализированных перенапряжений в материале, возникающих или вследствие резких изменений сечения или же каких-либо макро-, микро-или ультрамикроскопич. дефектов. Металлография. исследования показали, что при разрушении от усталости наблюдается появление линий сдвигов, иногда переходящих затем в трещины. Однако опыты Gough’a. и Hanson’а выяснили, с одной стороны, что появление сдвигов наблюдалось при напряжении ниже пределавыносливости (смотрите Усталость металлов), а с другой, что при споли-ровании уже появившихся линий сдвигов последующее разрушение может произойти и без появления новых линий скольжения. Т. о. механизм нарушения П. при усталости в основном происходит не путем пластич. деформации.’ По Haigh разрушение от усталости является результатом многократного перехода вещества из кристаллического в аморфное состояние, что является следствием микроскопич. сдвигов в многочисленных изолированных зонах. Объем этих зон настолько мал, что сдвиги эти не вызывают пластич. деформиррвания всего тела. Неоднократный переход из одного состояния в другое, связанный с определенным необратимым термодинамическим процессом, влечет за собой израсходование в этих зонах способности материала к пластич. деформации и затем разрушение. Приведенные факты заставляют за критерий для суждения о П.при многократно-повторной нагрузке принимать предел выносливости.

Особому рассмотрению подлежит прочность при ударном воздействии нагрузки (смотрите Удар). При ударном действии нагрузки разрушение в зависимости от условий может быть связано с определенной пластической деформацией или же быть хрупким. Если разрушение происходит лишь после того, как в деформируемом ударном объёме тела по соседству с изломом будет использована вся способность материала к упрочнению, то излом будет пластичным (Verfes-tigungsbruch, Gleitungsbruch). Наоборот, если разрушение произойдет путем расщепления решетки кристаллитов тела до того, как будут преодолены силы сцепления сдвигу, то разрушениеполучаетсяхрупким(Тгеп-nungsbruch). Тот или иной ход нарушения П. зависит естественно от того, какое из двух сопротивлений—сдвигам или расщеплению—меньше. Как сопротивление сдвигам, так и сопротивление расщеплению увеличиваются в результате упрочнения. Однако упрочнение против сдвига идет как правило быстрее, чем упрочнение против расше-

пления; в результате деформация при ударе начинается и идет путем сдвигов до тех пор, пока в результате большего упрочнения сопротивление сдвигам не станет больше сопротивления расщеплению. После этого только наступит разрушение расщеплением. В результате получается лишь частично хрупкий излом. Ряд условий может однако отодвинуть разрушение расщепления кристаллов на более раннюю стадию деформации. Так например, при понижении t°, при значительном увеличении скорости удара и особенно при наличии резких изменений сечения, например надрезе, степень деформированное™ до разрушения значительно уменьшается, и разрушение получается все более хрупким. В качестве критерия предельного состояния при ударе следовало бы принимать ди-намич. предел упругости и динамич, временное сопротивление. Так как эти величины обычно выше, чем статич. предел упругости и статич. временное сопротивление, то часто в запас П. при расчетах, например рельсов, исходят из свойств, определяющих П. материала при условии неударного загружения.

Те.ория П. в применении к расчетной практике. При всей принципиальной желательности расчет сооружений, машин и их деталей основывать на наиболее совершенных теориях П., например на учете энергии деформации, фактически в практике расчета применение этих теорий встречается только в качестве исключения, притом скорее исследовательского характера. Объясняется это, с одной стороны, трудностями математич. порядка, связанными с применением этих теорий, а с другой,—недостатком необходимых экспериментальных данных; в отношении различных материалов и различных случаев напряженного состояния. В связи с этим в практике расчета в отношении тел, обладающих одинаковыми механич. свойствами при растяжении и при сжатии, применяются только три теории П., именно теория П., основанная на учете главных нормальных напряжений (т.н. первая теория), теория, основанная на рассмотрении максимальных удлинений (т. н. в т о р а я те о-р и я) и наконец теория, исходящая из величины главных тангенциальных напряжений (т. н. третья теория П.).

Наиболее совершенной из них является, как выше было указано, третья теория, особенно, если вопрос касается материала, способного подвергаться пластич. деформации, или материала, разрушающегося путем скалывания. Весьма часто однако взамен этой теории применяют первую из перечисленных теорий. Расчет рельсов например основывают именно на этой первой теории, полагая, что такой подход лучше обеспечивает рельс от хрупкого излома. Такое решение однако не обеспечивает головку рельса от смятия в результате напряжений от изгиба и от смятия бандажом. Весьма часто из осторожности применяют комбинированную проверку и по первой и по третьей теориям П. Наряду с этими двумя теориями до сего времени широко распространена вторая теория П. Применение до сих пор этой теории, не отвечающей данным эксперимента, объясняется тем, что за длительный период ее распространения были выработаны на основе эксплуатонного опыта соответствую щие этой теории допускаемые напряжения. Т. о. несовершенства самой теории до некоторой степени коррегировались для обычных комбинаций сил и размеров нормами допускаемых напряжений. Из этого однако следует, что для случаев, выходящих за рамки типовых, применять вторую теорию П. безусловно не следует.

Т. к. чаще всего механические свойства материалов характеризуются результатами испытаний на сжатие или растяжение, то за исходную данность при расчете по всем трем теориями. принимают допускаемое нормальное напряжение при чистом растяжении; это допускаемое напряжение устанавливают в зависимости от требуемого коэф-та безопасности. Исходя из этого, согласно первой теории И., расчетная величина главного нормального напряжения не должна превосходить допускаемого нормального напряжения при чистом растяжении, по третьей теории наибольшее значение тангенциального напряжения не должно превышать половины допускаемого нормального напряйсения при растяжении, по второй же теории И. максимальное удлинение не должно превышать величины удлинения, соответствующего допускаемому нормальному напряжению при чистом растяжении, или, иначе, приведенное напряжение не должно превышать допускаемого нормального напряжения.

Для сравнения результатов, получаемых согласно различным теориям П., приводим следующие цифровые данные для отдельных частных случаев. Диаметры круглого вала, подверженного чистому кручению, подсчитанные по первой, второй и третьей теориям прочности, относятся, как 0,79:0,87 :1. Соответственно этому погонные веса валов будут относиться, как 0,62:0,76:1. Для случая комбинированного действия изгибающего момента М_х и крутящего момента М₃соотношения диаметров валов и погонных весов, получаемых в результате применения различных теорий прочности, представлены в таблице 1, где диам. и погонный вес вала, подсчитанные по третьей теорииП., принимаются за единицу.

Таблица 1.—С оотношения размеров и весов для вала согласно различным теориям П.

Соотношение между т х и Μζ	По 1-й теории П.		По 2-й теории п.		По 3-й теории П.
	Диам.	Пог. веса	Диам.	Пог. веса	Диам.	Пог. веса
ме=о.	1	1	1	1	1	1
	1	1	1	1	1	1
2 V- 2 — Αΐ х.	0.98	0.9L	0,98	0.93	1	1
мг=ых.	0.95	0.90	0,96	0.92	1.	1
	0,90	0,81	0,93	0,86	1	1
Μ X— 0..	0,79	0,62	0,87	0,76	1	1

Для случая растяжения пластинки в двух взаимноперпендикулярных направлениях, то есть при ffj=£0. ff₃=0, первая и третья теории приводят к идентичным результатам. Разницу же, получающуюся для этого случая в результате применения третьей и второй теорий, показывает табл. 2.

Для случая равномерного всестороннего растяжения, т.е. при σ₁=σ₂=σ₃>0, по третьей теории для однородного и лишенного пустот тела можно допустить бесконечные напря-

Таблица 2 .—С оотношение напряжений для пластинки согласно второй и третьей теориям.

1 Соотношение напряжений .	Допускаемое напряжение
	По второй теории	По третьей теории
<?2 = <г1.	1	1,50
2σζ=σ1.	1	3,20
10σ2=σ1.	1	1,03
σ2=0.	1	1,00

жения, по второй же и первой теориям разрушение должно иметь место уже при напряжениях конечных. Т. о. допускаемые напряжения, исчисленные по второй или по • первой теориям и по третьей теории, будут относиться, как 1: оо. Для различных сочетаний между а_гФа_гФа₃ отношения между допускаемыми напряжениями, исчисленными по третьей и по второй теориям, могут т. о. колебаться в любых пределах.

Эти примеры показывают всю опасность расчета сооружений по первой и второй теориям П., менее отвечающим результатам эксперимента, чем третья теория. Для тел с различными механич. характеристиками при сжатии и при растяжении все три перечисленные теории становятся неприемлемыми. В этом случае следует при расчетах П. базироваться на объёмлющих кривых Мора. Практически часто оказывается возможным эти кривые считать за прямые (фигура 2), что эквивалентно применению теории Кулона. Для чугуна, для которого временные сопротивления при сжатии и растяжении относятся, как 4:1, разрушающее напряжение, определяемое таким путем, для случая чистого сдвига будет равно 0,8 разрушающего напряжения при растяжении, что удовлетворительно согласуется с результатами опыта.

Для тел, П. которых резко различна в различных направлениях, весьма часто решающей является не величина наибольшего напряжения, а величина напряжения по тому направлению, по которому П. является наименьшей. Поэтому, например в отношении древесины, делается проверка не на главные тангенциальные напряжения, а на скалывающие напряжения вдоль волокон. Наконец определение безопасных напряжений на основе той или иной теории П. в отношении таких сооружений, как клепаные конструкции, железобетон и тому подобное., является операцией в значительной мере условной. С одной стороны, это происходит потому, что самое определение напряжений по методам строительной механики или теории упругости само по себе в отношении таких конструкций условно, а с другой—и потому, что такие сооружения в громадном большинстве разрушаются не в результате перехода основных напряжений за предел упругости или временное сопротивление, а в результате возникновения неустойчивых форм деформаций или местных напряжений, не учитываемых обычным расчетом.

Лит.: Тимошенко С. П., Теории прочности, Новые идеи в технике, сборник 1, П., 1915; его же, Курс сопротивления материалов, 9 изд., стр. 97—101, М— Л., 1930; Дав идеи ко в Η. Н., Механич. испытание металлов, стр. 105—144, Л., 1930; П и н е с Б. Я., Новые теории прочности, «Техника и производство», Л., 1927, 3; И о ф ф е А. Ф., Кирпиче- I

в а М. В. и Левит ска я М. А., Деформация и прочность кристаллов, «Труды Ленинградской физико-технич. лаборатории», М., 1925, вып. 1; Ьриджмен Дж., Проблема металлич. состояния, «"Успехи физических наук», М.—Л., 1930, вып. 3; Тимошенко С. П., Формулы сложного сопротивления с точки зрения различных теорий прочности, «Известия СПБ политехнического ин-та», СПБ, 1905; Mohr О., АЬ-handlungen aus d. Gebiete d. technischen Mechanik,

3 Aufl., B., 1928; NSdaiA., Der bildsame Zustand d. Werkstoffe, p. 39—50, B., 1927; TimoshenkoS. a. L e s s e 1 s J., Applied Elasticity, p. 497, Pittsburgh, 1925; Mesnager A., Les pierres, p. 80,130, 134, P., 1923; Mohr O., Ober d. Darstellung d. Spannungs-zustandes u. d. Deformationszustandes eines Korperele-menten, «Civil Ingenieur», Freiberg, 1882; Mohr O., Welehe Umstande bedingen d. Elastizitatsgrenze u. den Bruch eines Materials, «Ζ. d. VDI», 1900, p. 1534; Mesnager A., Limites de rupture et de ddforma-tion permanente, «Congres International pour l’essai des maliriaux, Amsterdam», La Hgye, 1927, t. 1, p. 15—38; Roth, Die Festigkeitstheorien, «Z»-ltschrift f. · Mathematik u. Physik», Leipzig, 1902, v. 48, p, 285; Haigh В. P., The Strainenergy Funktion and the Elastik Limit, «Engineering», L., 1920, v. 109; G r 1 f-1 i t h A. A., The Theory of Rupture, «Proc. of the First Intern. Congress for Applied Mechanics», Delft, 1924; M i s e s K., Mechanik d. festen Korper im plas-tisch deformablen Zustand, «Nachrichten d. Gesellschaft d. Wissenschaften zu Gottingen», Math.-Phys. Klasse, G6ttingen, 1913; H e n k у H., Zur Theorie plastiseher Deformationen, «Ztschr. f. angew. Mathematik u. Mechanik», B., 1924, B. 4, p. 323; KlrmSn Th., Festigkeits-versuche unter allseitigem Druck, «Z. d. VDI», 1911, p. 1749; F o p p 1 A., Bruchgefahr, «Mitteilungen aus demmech.-techn.LaboratoriuminMiinchen», Mch., 1900; Rosenhain W., The Plastic Deformation a. Fracture of Metals, «Congris International pour l’essai des matiriaux, Amsterdam», La Haye, 1928; Set wi nin g, Untersuehungen zur Erforschung d. Kerbschlagprobe, ibid., 1928; Becker, The Strength a. Stiffness of Steel under Bi-axial Loading, «Bulletin of the University of Illinois», 85; Guest, Strength of Materials under Combined Stress, «Philosophical Magazine», L., 1900, July; Ktrmin Th., Festigkeitsprobleme im Maschinenbau, «Enzyklopadie der math. Wissenschaften», B. 4, T. 2, H. 3, B.—Lpz., 1910; LodeW., Ver-suche iiber den Einfluss d. mittleren Hauptspannung auf d. Fliessen d. Metalle, «Ztschr. f. Physik», Berlin, 1926, B. 36; Westergaard, On the Resistance of Ductile Materials to Combined Stresses, «Journal of the Franklin Inst.», Philadelphia, 1920, May; Eos und E 1 c h i n g e r, Versuche zur Klarung der Frage d. Bruchgefahr, «Eidgen. Materialpriifungsamt», Zurich, 1926; Haigh B., Theory of Rupture in Fatigue, «Proc. of the First Intern. Congress of Applied Mechanics», Delft, 1924. H. Щапов.