Прыжок воды

Прыжок воды, такой вид неравномерного движения жидкости в открытом русле, когда наблюдается резкое повышении уровня потока при соответственном уменьшении его скорости. Глубины потока 1ь_г д о и Уь_г после Л. в носят название взаимных или сопряженных глубин и связаны зависимостью, получаемой из выражения для закона количества движения»

+ «>ι4=~ + "₂г₂₎ или f^/ij)=6(ft₂),

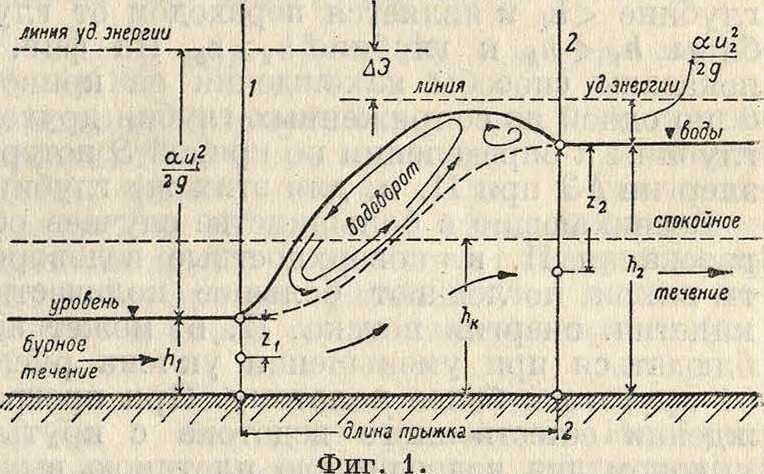
где θ(1ι) при данном расходе и форме русла есть ф-ия от наполнения h, Q—расход водотока, w и г—соответственно площади живых сечений 1—1 до и 2—2 после П. в и глубины погружений их ц. т. (фигура 1), <7=9,81 м/ск²

и а—коэф. перераспределения скоростей, принимаемый в среднем равным 1,1. Приведенная зависимость служит для определения взаимных глубин и fe₂, соответствующих двум одинаковым значениям Θ(Κ), называемой прыжковой функцией. Для случая широкого прямоугольного русла, для которого расход на единицу

ширины русла <?=γ, где I—ширина русла,

взаимные глубины определяются одна относительно другой ур-иями:

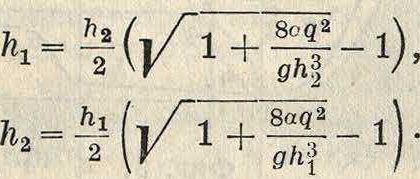
На фигуре 2 приведена кривая в(к) для этого· случая с расходом <7=1 м³/ск на 1 ж ширины русла. На этой фигуре также изображена для тех же условий кривая удельной энергии сечения Э(b). Эта величина, введенная Б. А. Бахметевым, представляет собой отнесенное к уровню дна среднее количество энергии Э, приходящееся на единицу веса жидкости, протекающей через сечение в единицу времени, и выражается ур-ием;

m=h + ^,

где и—средняя скорость потока. Как видно из фигура 2 кривая Э имеет минимум при некоторой глубине h_k, называемой к р и т и ч е-

ской глубиной. Для прямоугольного русла критич. глубина разна:

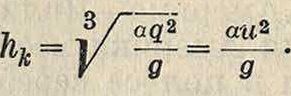
Для данного расхода при наполнении, равном критич. глубине h_k, знаменатель правой части диференциаль-ного ур-ия неравномерного движения жидкости (смотрите Гидравлика) обращается в нуль. В этом случае величина выражающая приращение глубины вдоль водотока, или tg угла на, клона его свободной поверхности, равна со, то есть поверхность воды как бы г а з» мгновенно подымается вверх нормально Фигура 2. к оси водотока,обра зуя П. в Следовательно П. в может возникнуть лишь при глубине < h_k и является переходом от глубины ftj < h_k к глубине h₂> h_k. На фигуре 2 показаны способы нахождения на кривой Θ по одной из сопряженных глубин другой глубины и определения по кривой Э потери •энергии Δ9 при П. в для этих же глубин.

Возникающие в большинстве случаев образования П. в поверхностные водовороты-вихри поглощают большое количество кинетич. энергии потока. П. в может наблюдаться при уменьшении уклона русла от крутого к более пологому. При преграждении естественного водотока с крутым уклоном дна водосливною плотиною выше •ее может образоваться П. в., расстояние которого от плотины определяется высотой последней. П. в может возникнуть при истечении воды из-под щита и при переливе через водосливную плотину или ниспаде-нии струи с перепада и быстротока с большой скоростью в русло с малым уклоном. В последних случаях (фигура 3) различают

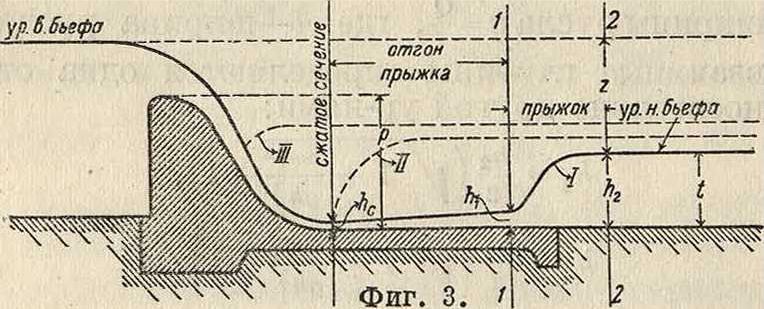
три формы сопряжения ниспадающей струи •с глубиной нижнего бьефа ί: 1) с отогнанным П. в.— I, 2) надвинутым П. в.—II и 3) затопленным П. в.—III. Та или иная •форма сопряжения зависит от соотношения: глубины t, разности уровней бьефов (перепада) г, высоты стенки падения р и энергии сжатого сечения. Если сжатое •сечение h_c сохранить постоянным, а глубину t постепенно уменьшать, начиная с формы III, то при определенной глубине возникнет надвинутый прыжок II, образующийся в месте нахождения сжатой струи. При дальнейшем уменьшении t наступает явление отгона прыжка в положение I, когда,

глубина h₂, взаимная с глубиной h_t ниже сжатого сечения, превышает глубину нижнего бьефа t.

Отогнанный П. в вызывает появление значительных скоростей, распространяющихся подчас на большую длину и крайне разрушительно действующих на ложе потока, а потому вызывающих необходимость солидно укреплять его. Поэтому при устройствах по сопряжению бьефов гидротехнич. сооружений и в других случаях стремятся не допустить образования отогнанного П. в., что достигается или затоплением Л. в или способами беспрыжкэвого соединения двух глубин потока, меньшей и большей критической (смотрите Водобой). Для определения, будет ли П. в отогнан или затоплен при истечении воды через перепады и водосливные плотины, обычно пользуются критерием Б. А. Бахметева, по к-рому отогнанный

П. в получается при условии ^ где

) ₀ есть минимальное(критическое) значение относительного перепада^, при к-ром П. в уже образуется. Для затопления П. в необходимо соблюсти условие > Значения (J^определяются по кривым Бахметева.

Для определения формы П. в при истечении воды из-под щита весьма удобно пользоваться таблицами и кривыми, составленными А. А. Угинчусом.

Лит.: Бахметев Б. /А., О неравномерном движении жидкости в открытом русле, СПБ, 1912; его же, К вопросу о расчете перепадов, «Совещ. по опытностроительному делу», IX., 1916, вып. 1; Чарномский В. И., Задачи на установившееся неравномерное течение воды в открытых прямых руслах с прямоугольным и трапецоидальным поперечным сечеяием, CIIB, 1914; Павловский Н. Н„ Х^идравлич. справочник, стр. 134—138, Ленинград, 1924; Угинчус А. А., Графич. определение взаимных глубин при прыжке воды в прямоугольном русле, «Изв. научно-мелиорационного ин-та», Л., 1926, выд. 11—12; его ж е, К вопросу о расчетево-добойных колодцев, там же, 1929, выя. 19, стр. 158— 293; Рахманов А. Н., Графики критич. и взаимных глубин, гидравлич. показателей, модулей расхода и иек-рых других гидравлич. величин для трапецеидальных русел, там же, 1929, вып. 18; Журив В. Д., Погашение энергии в перепадах и быстротоках, «Вестник ирригации», Ташкент, 1927, 5, стр. 33—53; А х у т и н А. Н., Примеры гидравлич. расчетов в области неравномерного движения воды в открытых руслах, стр. 24—143, М., 1928;

Н i n d s J., The Hydraulic Jump a. Critical Depth in the Design of Hydraulic Structures, «Engineering News-Kecord», N. Y., 1920, v. 85, 22; Cr eager W. P. a. J ustin J.D., Hydro-Electric Handbook, 142—151, New York, 1927; Koch A. und C a r s-tanjen M., Von d. Bewegung des Wassers u. den dabei auftretenden Kralten, p. 83—92, 162—165, Berlin, 1926. С. Каплинсний.