 > Техника, страница 74 > Прямая и обратная геодезическая задача
> Техника, страница 74 > Прямая и обратная геодезическая задача
Прямая и обратная геодезическая задача
Прямая и обратная геодезическая задача. Прямая геодезич. задача заключается в том, что, имея география, широту φ„ и долготу La точки А на местности и длину линии 8 и азимут ее а на другую точку В местности, по этим данным вычисляют география. широту ψι, долготу Lt точки В и обратный азимут а1 с точки В на точку А местности. Эта задача применяется в практике геодезич. работ при вычислении пунктов триангуляции (смотрите) для съемки и составления карт больших площадей. Т. к. земной шар представляет собой сложное тело вращения—геоид, весьма близкое к эллипсоиду вращения, то в зависимости от расстояния между точками А я В приходится применять те или иные ф-льт, принимая при малых расстояниях между точками 1иВ поверхность земли за шаровую или при больших расстояниях за поверхность эллипсоида, причем существуют различные поправочные члены и видоизменения основных ф-л для весьма больших расстояний. Способов решения этой задачи имеется несколько; из них следует отметить формулы, предложенные Шрейбером, Кларком, Гауссом и Бесселем. Ниже приводятся способ и ф-лы Шрейбера, как наиболее употребительные для практич. целей вычисления пунктов триангуляции при расстояниях, не превышающих 60 км.
Даны iра, L„, а и S. Найти: щ, L&, а,.
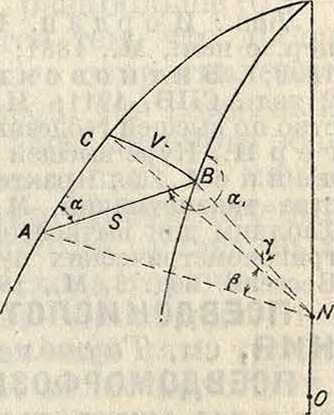
Формулы в окончательном виде следующие (смотрите фигура):
U=S COS а, V — S Sin а,
β=(1)„υ, у=(2)со
lgb=lgJ5-(4)[ + (5)i:2;
lg о=Ig
У-|(5 )U2;
τ=C tg (?>„ + b),
A=c SC (<pa + b),
6=с T,
be
‘ ~ 2e 1 1 lg t=lg τ ·&- ir2 - - iA2,
lg l=lg A - vr2,
lg d=lg <5 - >T2 - V/2.
В результате найдем:
<Гb=?β + i1 - d,
Οι=180° “Ь о-j- t — ε.
Lb — La + l.
(1)
(2)
(3)
Коэф-ты (1), (2), (3), (4), (5) зависят от географической широты места и берутся из специальных таблиц, также и величина v. Таких таблиц имеется несколько и они основываются на различных размерах земного эллипсоида, определенных в разное время отдельными учеными. В производстве в СССР применяются таблицы Шарнгорста, вычисленные по размерам земли, определенным Бесселем.
Обратная геодезич. задача заключается в определении длины 8 и ее прямого а и обратного азимутов по данным географич. координатам ее концов <ра, La точки А и <рь, Ц, точки В. Задача решается по тем же ф-лам, но в обратном порядке при тех же обозначениях:
L — Lb—La, τ=I sin φΐι, lg A=lg l + rr2,
6=(3)bl2 Sin <Pb COS <Pb< lg d=lg <5-
<Ра=’Ра+b =<Pb + d,
c=A COS Oil + b), b=Oa +6)- φ„,
П-Ш
νχ- — V/β,
2 4
tg a =
U’
lg ί=Ig г
(4)
X=С tg Οα + b),
--νλ‘1; S=~-=2 COS a
(2)c ’
1
1. _
2 2 COS a Sill a ’
o.=cl -f-180° ~j~ t — ε,
]§β=^ b+ (4)a U-(b)a ϋ2·
b e
величина^
Q
= sin 1";
(0)
(5)
ρ—радиус круга, выраженный в секундах дуги.
Лит.: Иордан, Руководство высшей геодезии, пер. с нем., М., 1881; К л а р к А., Геодезия, СИБ, 1890; Витковский В., Практич. геодезия, 2 изд., СПБ, 1911; ИвероновИ. А., Руководство по высшей геодезии, ч. 1, 2 изд., М., 1926; Ц Инге р Н., Курс высшей геодезии, СПБ, 1898; Ф и лоне н к о А.’ С., Практич. руководство для производства триангуляции, М., 1927; Шарнгорст К., Таблицы для вычисления широт, долгот и азимутов тригонометрических пунктов 1-го класса насфероиде Бесселя, изд. 3, М., 1927. Н. Веселовский.