> Техника, страница 75 > Пупинизация

Пупинизация

Пупинизация, искусственное увеличение самоиндукции линии (воздушной или кабельной) посредством специальных катушек самоиндукции (катушек Пупина), включаемых в линию через регулярные промежутки последовательно с проводами.

В Ϊ893 году Хивисайд (О. Heaviside) в своих исследованиях о значении самоиндукции при распространении разговорных токов по проводам обратил внимание на то, что затухание, вызываемое линией, м. б. уменьшено путем искусственного увеличения самоиндукции линии. Он указал, что увеличение самоиндукции м. б. произведено при помощи катушек, включаемых в линию на определенном расстоянии. Эта идея получила практич. осуществление в 1900 г. благодаря Пупину, который, исходя из аналогичной механич. проблемы Лагранжа (колебания натянутой струны, масса которой увеличивалась с помощью шаров, подвешиваемых к струне на определенных расстояниях), вывел ур-ие для определения расстояния между катушками и дал расчет катушек!

Возможность уменьшения затухания β {см. Бета) путем увеличения самоиндукции L объясняется тем, что в уравнении

P-Wr + iV%-i + i^z

для телефонных линий первый член значительно больше второго. Если бы было наоборот, то пришлось бы для уменьшения β увеличивать емкость С. Кривая первого R 1 ГС R

члена ~2 у ΙΓ ⁼ 2~ представляет гиперболу; второй же член ~Ζ выражается прямой .линией, проходящей через начало координат. Сумма ординат дает кривую затухания β в зависимости от Ζ она имеет минимум в точке М, соответствующей точке пересечения S (смотрите фигура 1). Если волновое сопротивление какой - либо линии равно отрезку О А, то затухание ее будет равно отрезку АР. Увеличивая волновое сопротивление Ζ этой линии до величины, соответствующей отрезку ОБ, мы достигнем минимального затухания β. Увеличить же *-П мы можем или путем увеличения L или уменьшения С,

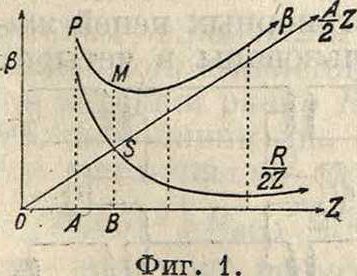
но уменьшение емкости С м. б. достигнуто лишь в весьма, незначительных пределах; следовательно остается одно средство для уменьшения β—увеличение, самоиндукции; Если это увеличение самоиндукции производится при помощи катушек, включаемых в линию, то линия в честь Пупина называется пупинизированной и катушки—пупиновскими.

Пупинизированная линия состоит из ряда последовательно соединенных .звеньев. Каждое из звеньев содержит отрезок однородной линии длиной-5, причем либо в середине этого участка (фигура 2) включена пу-

j	- S -		- S —		— s ------«
-i		s s	—	i=i
2	П5	2 : г		2 2	S 2 ·
		ппгг
Ϊ& ; 2		2 2 _УТЯЯГХ^5У1У -			2 --ои :

Фпг. 2 и з. пиновская катушка с кажущимся сопро-; тивлением W_s=R_s + ia>L_s либо по концам его включены две половины катушки с кажущимся сопротивлением.(смотрите фигура 3). He^J

3 j

трудно убедиться, что пупинизированная линия представляет собой дроссельный фильтрующий контур (смотрите) или 1-го рода (фигура 2) или 2-го рода (фигура 3). Заменяя например на фигуре 2 каждую половину участка линии конденсатором соответствующей емкости и присоединив самоиндукцию линии к самоиндукции катушки, получим схему

j(Lg*L)S

- i : " jCKS —. =	—jCA
I -. ·-· · · »:-1-ггфГОБЯГ-

торая представляет не что иное, как дроссельный фильтр, где iiijiw

L_s — самоиндукция Фигура 4.

катушки, отнесенная на 1 км линии, L—самоиндукция 1 км линии, S—расстояние между пупиновскими катушками, С*—емкость 1 км линии. Тогда собственная частота одного звена пупинизирЬ-ванной линии будет равна:

1 2

си₀= -

V

(.L_s + L)S

CiS J/(L_s + L)C*S3

SV(L_s + L)Ci

Известно, что дроссельный фильтрующий контур пропускает с ничтожным затуханием“ лишь частоты, лежащие ниже соб-_:ственцой частоты звена контура. Следовательно для ω₀ пупинизированной линии мы должны выбрать величину возможно ббль-шую по сравнению с высшими разговорными частотами; в противном случае некоторые разговорные частоты не будут переданы, и речь будет воспринята в б. или м. искаженном виде. В настоящее время пупини-зируются исключительно кабельные линии; П. воздушных линий, имевшая прежде широкое применение в целях уменьшения сечения проводов, в настоящее время, с введе-

17

Т Э. т. XVIII.

нием в экеплоатацию усилителей, потеряла свое практическое значение. П. воздушных проводов имела сомнительную ценность вследствие того, что затухание пупинизиро-ванной линии в сильной степени зависит от проводимости изоляции, колеблющейся в воздушных линиях в больших пределах.

Затухание пупинизированной линии. Исходным ур-ием, служащим для определения затухания пупинизированной линии Ь, служит следующее:

ch3=chyS + H-shy£, (1)

гдед= (5 + га)—постоянная распространения

Таблица 2.—3 н а ч е н

Величина b₀ по уравнению (2) нуждается в некоторой детализации. Во-первых, величина. Rs^S R_s, то есть омич, сопротивление пупи-новской катушки не является постоянной величиной, ибо зависит от частоты переменного тока. Величину R_s можно подразделить на две части: —сопротивление постоянно му и Rp—сопротивление переменному току. Результаты измерений величины Rp в зависимости от круговой частоты для катушек, самоиндукция L_s которых равна: 0,20;” 0,10;. 0,07; 0,14; 0,056 Н, приведены в таблице 2. Во-вторых, проводимость изоляции А_к кабеля обусловливается почти исключительно· (принимая во внимание весьма высокое· ия величин Rp.

	со	Rp		«	Rp		(О	Rp		со	Ир		со	Rp
	1 οου	0,39		1 000	0,37		1 000	0,13		1 000	0,26		1 000	0,104
се	3 000	1,28	со	3 000	1,21	о	3 000	0,43	о	3 000	0,86	о ю	3 000	0,341
	4 000	1,78	—I	4 000	1,69		4 000	0,58	II	4 000	1,16	II	4 000	0.465
If	δ 000	2.32		5 000	2,20	V 8	о 000	0,77	8	5 000	1,54		5 000	0.62
V	7 000	3,51	ад	7 000	3,34	ад	7 000	1,16	ад	7 000	2,34		7 000	0,93
	8 000	4,16	σ>	8 000	3,95	о	8 000	1,38		8 000	2,76	ю	8 000	1,10
C-J	10 000	5,60	£	10 000	5,25		10 000	1,95		10 000	3,90		10 000	1.56
о	12 000	7,15		12 000	6,80		12 000	2,50	И	12 000	5,04		12 000	2,03
у	15 000	9,70	ад	15 000	9,25	ад	15 G00	3,41	05 ад	15 000	6,83	V со ад	15 000	2,75 1

пупинизированной линии; γ=(β + га)—постоянная распространения однородной линии на участке S между пупиновскими катушками; Ζ—волновое сопротивление однородной линии на том же участке; R_s—кажущееся сопротивление пупиновской катушки. После ряда соответствующих преобразований получим:

+ ^:

b-)Vb+^rrV

л. л Г Lg 1 kS

ί C.t. J /ΐ-ηϊ ’

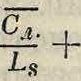
где R_k—омич, сопротивление 1 км кабельной линии; С_л.=C_k + С»—емкость 1 км линии, состоящая из емкости кабеля С_к и емкости C_s между обмотками пупиновской катушки, отнесенной на 1 км линии; L_s— самоиндукция катушки, отнесенная на 1 км линии; А_л= A_k+A_s—проводимость изоляции линии, состоящая из проводимости изоляции кабеля и пупиновской катушки, отнесенной на 1 и линии; η=—, где ю₀—соб-

COq

етвенная круговая частота пупинизированной линии; %—коэф., причем

7,- Г. ^2Ж- -V- γ -^η(1~^η2)·

lx+ ’

^b»^=s[f(¹-l^r2)y^riⁱ‘ +

+уК&-+^а#/Я· ⁽²>

Для определения к, зная х, можно пользоваться табл. 1.

Таблица 1.—Д ачные для определения к о э ф и ц и е н т a h.

X	h	X	k	X	k	X	k	X	k
0,00	0,000	0,30	0,668]	0,70	0,854]	1,60	0,958	6,0	0,997
0,05	0,308	0,35	0,705|	0,80	0,877	1,80	0,966	7,0	0,998
0,10	0,425	0,40	0,736	0,90	0,896	2,00	0,972	8,0	0,998
0,15	0,508	0,45	0,763	1,00,	0,911	3,0	0,986	9,0	0,998
0,20	0,573	0,50	0,789!	1,20	0,93a,	4,0	0,992	10,0	0,999
0,25	0,625	0,60	0,824)	1,40	0,947	5,0	0,996	20,0	1,000

сопротивление изоляции постоянному току) диэлектрич. потерями и выражается следующим образом:

А_к=«>С_к tg <5“,

где <5_&—угол диэлектрич. потерь. Так как для спектра разговорных частот С_к и tg 6_км. б. приняты постоянными величинами, то проводимость изоляции А_к пропорциональна круговой частоте со. Для междугородных кабелей tg 6_к зс 4,8 · 10^_3. В третьих, проводимость изоляции между обмотками пупиновской катушки

as=ω с; tg <5_S,

причем для пупиновской катушки из эмалированных проволок можем принять: C_s== 0,0025 1(Г⁶ F и tg δ_$=0,015; поэтому C_s tg <5_S=37,5 · 10^-12. Следовательно

if (^ι-ι^^,)Κξ+

R 4* R

V

Ao

y 1 — i

(3>

Километрическое же затухание β будет;

β-ί

Ур-ие (3) будет справедливо, если жилы кабеля используются только для образования двухпроводных линий. Если же жилы кабеля используются также иными способами, то в ур-ие (3) надо ввести добавления.

Для образования разговорных цепей жилы кабеля м. б. использованы в четырех комбинациях.1) Одна пара жил кабеля образует двух-проводн. основную линию. 2) Каждые две основные двухпроводные линии образуют четырехпроводную искусственную линию (смотрите), которая следовательно не занимает специальных жил кабеля (фигура 5, Т — телефонный аппарат), причем одна основная двухпроводная линия служит прямым, а другая основ-

4		rtf f
Ίη		/· L·
1?		4 ф
Фигура 5.

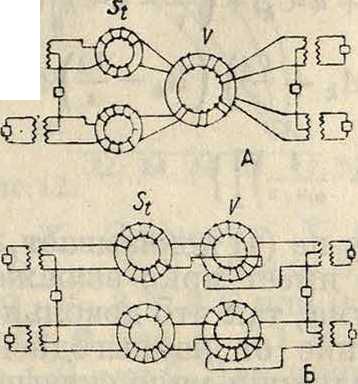
Фигура 7.

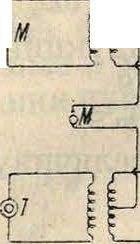
нал двухпроводная линия—ооратным проводом. 3) Две пары жил кабеля (то есть четыре жилы) образуют четырехпроводную основную линию, причем разговор в одну сторону проходит по одной паре, а в другую сторону—по другойХфигура 6, Т—телефон, М—

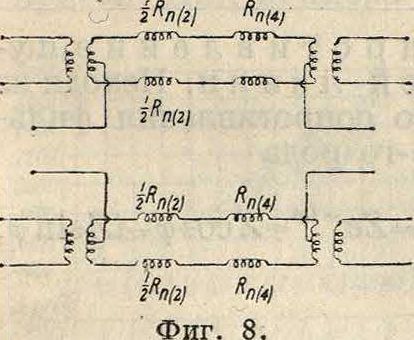
микрофон). 4) Ка-Ьм £П Г|| ^ ждые две четырех проводные основные линии образуют искусственную Ί восьмипроводную - линию, которая еле-довательно не за-^{иг ь}* нимает специаль ных жил кабеля, причем одна основная четырехпроводная линия служит прямым, а другая—обратным проводом. На фигуре 7А показано включение пупиновской катушки как в двухпроводную основную, так и в четырехпроводную искусственную линии. Если принять, что катушки S_t служат ^ для увеличения само-индукции основных (двухпроводных) линий, а катушки V— для искусственной линии, то катушки V надо так включить, чтобы для основных линий они представляли собой только омическое сопротивление, и наоборот, для искусственной линии катушки S_t должны являться только омич, сопротивлением. Из фигура 7А и 7Б видно, что поставленная задача о включении катушек в основную и искусственную линии м. б. решена двумя путями: 1) в искусственную линию включаются две катушки (способ Сименса) п 2) в искусственную линию включается одна катушка (способ Вестерн Электрик К°). Обозначим буквой В_п(2> омич, сопротивление постоянному току катушки основной линии, то есть сопротивление катушки при последовательном соединении обеих обмоток (фигура 8), отнесенное к 1 км линии; таким образом сопротивление каждой обмотки равно 72^«(2>· После этого обозначим через H₂R_nU > омическое сопротивление постоянному току каждой катушки искусственной линии при параллельном включении ее обмоток; следовательно сопротивление каждой обмотки одной катушки равно R_nuy Так. сбр. в искусственной линии две катушки основной линии увеличивают омич, сопротивление на

2 · 4 В_п(о=Q/км; а в основной линии—катушки искусственной линии увеличивают сопротивление на 2 й_7г(4) Q/км. Поэтому километрич. затухание двухпроводной линии будет:

для искусственной же линии:

4) —	iiA<4)(l -fo,
V	Ls(. 4 ) 2

V,

LM 4)

4)

2

(4)

где L_s(2)—самоиндукция катушки основной линии (на 1 км) при последовательном соединении обмоток; I._s(4)—самоиндукция, отнесенная на 1 км и вносимая в искусственную линию двумя последовательно соединенными катушками V (фигура 7А); С_л.₍₂₎— емкость двухпроводной основной линии на 1юн; <7_г.<₄₎—емкость искусственной четырех-нроводной линии на 1 км; j;_<2)=—--для ос-

о ад О)

новнои двухпроводной линии; г₍₄₎=— —

^ω0 (4)

для искусственной четырехпроводной линии;

^ω0(2) ^ω0<4> ⁼

1

S vлХи)

Зависимость между ω₀₍₂₎ и ω₀₍₄₎ определяется: 1) способом свивания жил кабеля и 2) тем требованием, по которому километрич.

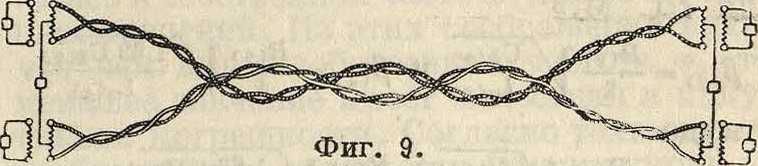
затухание для средних разговорных частот (со s 5 ООО) как искусственной, таки основной линий должны быть между собой равны. Существуют три способа свивания жил междугородного кабеля, которые получили распространение в настоящее время: 1) способ Ди-зельхорст-Мартина (фигура 9), сокращенно «Д. М.»; 2) способ «звездочки» (фигура 10),

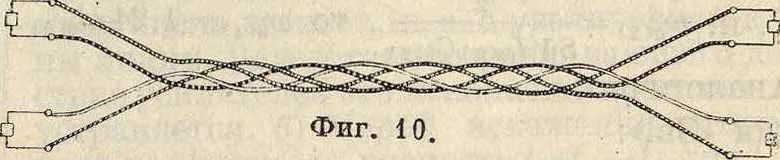
сокращенно «Зв.»; 3) способ «двойной звездочки» (фигура 11), сокращенно «Д. Зв.». Способ «Д. М.» заключается в том, что две жилы, образующие пару, перевиваются между собой в виде винтообразной линии, а каждые две пары, образуя четверку, перевиваются в свою очередь между собой также в виде винтообразной линии, причем шаги винтовой линии пары и четверки должны отличаться друг от друга. Способ «Зв.» состоит в том, что не две, а четыре жилы перевиваются между собой по винтообразной линии, образуя четверку. Способ «Д. Зв.» состоит в том, что сперва две жилы, образующие пару, перевиваются между собой по винтообразной линии; затем такие четыре пары перевиваются между собой по винтообразной

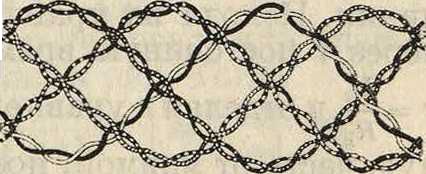
Фигура 11.

C.l.i 2)

V¹

линии, образуя восьмерку (двойную четверку),· причем искусственные лцнии образуются из двух пар, лежащих по диагоналям. Отсюда видно, что расположение жил в кабеле в зависимости от способа свивания различно; это различие обусловливает определенное соотношение между емкостью С_к(а) двухпроводной и емкостью C_k(i) четырехпроводной линии. Согласно измерениям имеем:

1) для «Д.М.»: £«И=1,63,

ЬА(2>

2) для «Зв.»: g^f-2,8,

откуда

ch 2 Ь=ΆΡ +N² + V(M² + N²+ 1)²-4М². Диференпируя это ур-ие по L_s, найдем наи выгоднейшее значение L_s. Из ур-ия дм

Im~ + n

dL dL

)(

dL

dL

dLo dL_s

3) для «Д. Зв.»:=1,2.

Поэтому, принимая во внимание, что β₍₂₎ рав-

получим искомую величину самоиндукции:

γ, _ 2Ζ т п ch 2β S - cos 2α S ^s ~~ co m² + η² n sh 2β S - m sin 2a S и соответствующую минимальную величину затухания:

^ 2Ь — ^{n2 ch cos 2a s}

m² -f-n²

Выражая а и β через R_k, L_k, С_k я A_k и разлагая гиперболические и круговые функции в ряды, получим:

- Jci) t¹ +f

ch 2Ь=1

2S2

ί¹ + Js) {^A* + T+f [²(^β* “ ^(A*^{+ +} (т⁵ ~ ^02C*)^(R*^C*^{+ Al4)}] } ’

V {(4k + Щ) + T[(4 + (й“-т) ^<АЛ-^с_к) +

^)Β·

( (4)

ι +

но /?₍₄₎, приближенно можем положить: для «Д. М.»

О К(2) Л ГC/fC2) „ О 11(2) л/~ 1

63 С/_£(2)

Ls(i)

откуда

#(2) Ί /~С/с(2) -R(2) 1 /"1,

2 У Lg (2) 4 Г

63 СЖ2)

И

-l-si4) 0,406 »

следовательно

^ω0(4> ⁼

S | о",406 L_s(2) · 1,63 Сд(2>

2 2

= 1,24-

S /L_s(₂)C_A(2) К0,406 -1,63 S |/L_s(2) С_Л(2)·

ГГ-1 2

Т. к. О)₀₍₂₎=-

S l^/b_s( 2) С,.(2 >

, то о>₀₍₄₎=1.24 ω₀₍₂₎.

Аналогично:

для «Зв.»:

L_s(i) ⁼ ^ ^s(2, И hi₀₍₄)=0,71 Ct>₀(2),

для «Д. Зв.»:

4>⁼ С,3 J0_S<а) и со₀₍₄₎=1,6э О)₀₍₂₎.

Теоретически наивыгоднейшей величиной самоиндукции пупиновской катушки назовем ту ее величину, которая обусловливает минимальное значение затухания пупинизированной линии. Исходя из уравнения (1), обозначая через т постоянную времени катушки, то есть г=и отделяя в уравнении (1) действитель-

^Rs

яую часть от мнимой, получим:.

ch Ь cos а — ch β S cos a S —

— (иг sh β S cos a S + n ch β S sin a S)=M,

sh b sin a=sh β S sin aiS— AZ (^{m cl1} β ® sin a S — n sh β S cos a S)=N, где

m=— sin w — cos ®;

^τ ωτ

n=cos φ — —sin w: Z =Ζβ^ιφ,

¹ ωτ τι

Ур-ие (4) показывает, что кривая затухания не имеет ярко выраженного, острого минимума, так что довольно значительное отклонение от наивыгоднейшей величины самоиндукции мало сказывается на величине затухания. Но, с другой стороны, из этого уравнения следует, что наивыгоднейшая величина L_s зависит от круговой частоты переменного тока. Как пример в таблице 3 приведены результаты вычислений L_s при ω=5 000 (7?_fc=11,5 Ω; Lfc=7 · 10^-4 H; A_k=1 · 10~⁶ сименс, С_к=41 · io^-8 F) и при ,ω=10 000 (А_к =2 · 10^-6) для различных S.

Таблица 3.—Значения L

S	Ls ПРИ а>=5 000	Ls при «,=10 000
2	0,162	0,0777
: 5	0,069	0,027

Волновое сопротивлениепу-пинизированной линии. Исходя из ур-ия, для волнового сопротивления фильтрующего контура 1-го рода

Ζ=· —р^== =Ζβ~^1φ =Zcos φ—iZsin ?>,

V a y_i+R_a

получим:

Zcos 9-кУс -у^	(5)
	(6)

к-рыми надлежит пользоваться в том случае, если первая пупиновская катушка располо-

жена на расстоянии -₂, равном половине расстояния между катушками (выражения для величин к и b смотрите выше).

Если же первая пупиновская катушка расположена на каком-либо расстоянии X, то для волнового сопротивления служит следующее выражение:

²=УШ^М

-N),

(7)

где Μ =

Vi-

, а N =ιη

1-2-

—ΙΚ)

Ыа фигура 12а и 126 построены действительные и мнимые части волнового сопротивления пупинизированной линии в зависимости

]/£

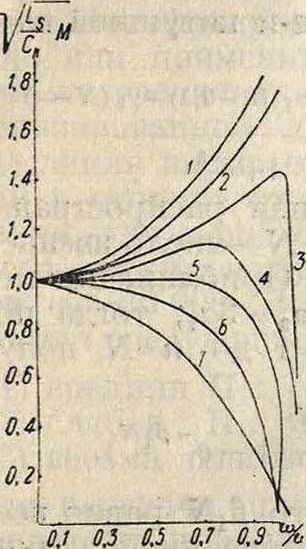
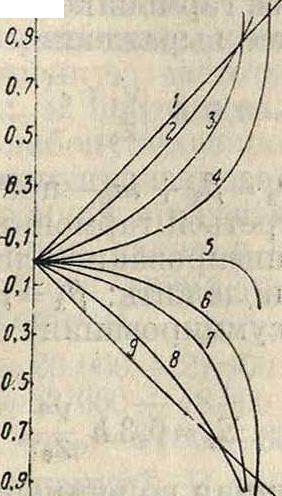
Фигура 12.

02 0.4 0.6

1.0 %.

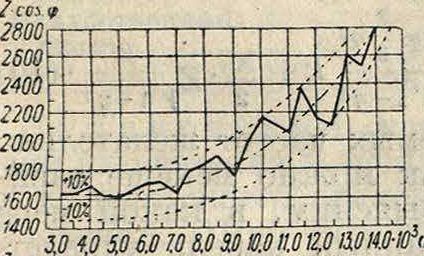
от. η для различных X. Значения×для кривых фигура 12а: 0,5 S для 1, 0,4 S или 0,6 £ для 2, 0,3 S или 0,7 S для 3, 0,2 S или 0,8 S для 4, 0,17 S или 0,83 S для 5, 0,1 S или 0,9 S для 6, 0,0 или 0,1 S для 7. Для кривых фигура 126: 0,0 для 1, 0,17 S для 2, 0,3 S для 3, 0,4 S для 4, 0,5 S для 5, 0,6 S для 6, 0,7 S для 7, 0,83 S для 8,1,0 Ядля 9. Ур-ия волнового сопротивления пупинизированной линии (4), (5) и (6) показывают однообразное изменение в зависимости от частоты, то есть эти ур-ия м. б. построены в виде кривых, имеющих нек-рую плавную закономерную форму. В действительности же волнов.оесо-противление пупинизированной линии очень неравномерно, и кривая его, построенная на основании результатов измерений * имеет неправильную волнистую форму и колеблется около некоторой средней линии, совпадающей с теоретической (вычисленной) кривой. Для примера на фигуре 13 представ-ленытеоретическая и действительная кривые волнового сопротивления пу-пинизирован. кабеля. Так как форма кривой волнового сопротивления, линии имеет весьма важн. значение для настройки промежуточных усилителей, а также и для безискаженной пе-

200

0

200

400

~-+к -101

Я И и Ы 10 М 30 ШМООШ 1.0 Л Фигура 13.

редачи речи, то вопрос об уменьшении или уничтожении волнистости кривой волнового сопротивления и о приближении ее к теоретич. кривой имеет весьма важное значение. Подробные исследования этого вопроса показали, что эта волнистость обусловливается погрешностью как в изготовлении кабеля (неодинаковая величина емкости во всех.звеньях пупинизированной линии), так и пупиновских катушек (неодинаковая само индукция катушек), что вызывает изменение собственной частоты звена пупинизированной линии. Погрешность эта выражается соответственно следующими величинами: для кабеля

ΔΟ/ί 1 —2 b

щ - ---

Ск и для катушек

Vef-

п_п=-

AL

- γ

-2 b

Следовательно погрешность обусловливается: 1) величиной относительной погрешности емкостей и самоиндукций

Wi ^J-‘S

2) расстоянием неоднородного звена от начала линии (затухание b) и 3) отношением При прочих равных условиях волнистость кривой волнового сопротивления имеет наибольшее значение, когда неоднородно первое звено пупинизированной линии. Ф-ия — ¹, определяющая завн-

симость погрешности от частоты, изменяется с возрастанием частоты от 0 (при со — 0) сначала очень медленно, а затем, приближаясь к собственной частоте, достигает больших значений. Из этих соображений видно, что чем выше собственная частота ω₀, тем меньшее значение имеет емкостная и индуктивная погрешности. Согласно техническим требованиям погрешности самоиндукции катушек и емкости участков П. (на длину S) не должны превышать ±1,5% от нормальных значений.

Искажения, вызываемые пупинизированной линией (обискажениях формы кривой разговорного тока см, Телефонная передача). а) Искажение первого рода пупинизированной линии весьма значительно; оно возрастает с увеличением числа звеньев, то есть с увеличением длины линйи. Вследствие выравнивающего действия усилителей это искажение практически устраняется, б) Мерой искажения второго рода принимается разность <=ί₂—где — время, потребное для пробега вдоль линии группе волн самых низких частот, а <₃— время, за которое к концу линии подойдут вбе группы волн, частоты которых образуют передаваемую волну сложной формы. Для пупинизированной линии длиной I км

[——1—— — ιΊ· (8)

_______ Л.

S"0 1 ω 2

ly^u) J

о ур-ие, pa:

)бках в ряд.

Преобразуем это ур-ие, разложив знаменатель дроби в скобках в ряд. Тогда

По постановлению Консультативного международного комитета по дальней телефонной связи для всего спектра частот 300— 2 400 пер/ск. величина t не должна превышать 30-10^-3 ск.

Поэтому

30·10~³<^ί^^

_шз о _ 7 5. ю»=к,

откуда

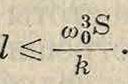
Ур-ие (9) говорит, что при заданных S и к дальность телефонирования по пупинизйро-ванной линии обусловливается собственной частотой линии и при желании увеличить дальность телефонирования (то есть длину линии I) должен быть увеличена собственная частота линии со₀, иными словами, самоиндукция линии (катушек) должна быть уменьшена. В табл. 4 указана численная зависимость (по уравнению 9) между 1_тах и ω₀ при различных величинах S.

Таблица 4 -3 а в и е и м ость м е ж д у 1_твг и ®₀при различных величинах S.

S —	2 км	S =	, 7 КМ
1 max В ИМ	о>0	1-тах В	а>0
700	13 800	600	13 800
900	15 000	760	15 000
1 730	18 200	1 360	18 200
2 600	21 400	2 200	21 400
3 200	23 0СО	2 700	23 000
4 150	25 000	3 500	25 000
5 200	27 000	4 500	27 000
7 200	30 000	6 100	30 000

Итак, для устранения искажений 2-го рода в пупинизированной линии требуется повысить ее собственную частоту со₀, что достигается путем уменьшения ее самоиндукции L_s. Но это средство имеет тот недостаток, что обусловливает собой увеличение затухания, благодаря чему потребуется или укрупнять диаметр жил кабеля или увеличить усиление телефонных токов путем увеличения числа усилителей. Не говоря уже о том, что оба приведенные мероприятия вызовут повышение стоимости первоначального оборудования,.они вызывают совершенно невозможное положение в эксплуатации, так как при дальнейшем увеличении длины линии придется увеличивать число усилите- ; лей в существующей линии, иными словами, | учащать число пунктов, в которых расположены усилители. Поэтому необходимо иметь такое средство, устраняющее искажение 2-го рода, к-рое позволило бы производить увеличение длины линии без каких-либо переделок существующих линий. Очевидно, что в линию должен быть включены какие-то добавочные контуры, которые уравновешивали бы скорости распространения по кабелю различных частот разговорного тока. Такими контурами являются т. н. скрещенные контуры (смотрите Фильтрующие контуры). в) Искажение 3-го рода (нелинейное искажение). Если в начале пупинизированной линии действует синусоидальное напряжение | Vi, то на конце линии, замкнутом далее на ! свое волновое сопротивление, вместе с основной частотой появляются также и ее гармоники, из которых 3-я гармоника имеет наибольшую амплитуду. Если через пупинов-скую катушку проходит ток [Ij sin (o>t — φ), то на зажимах катушки возникает напряжение, содержащее 3°-ю гармонику, равную где

Е=0,6 ii|J|²sin (3ωί — 3φ),

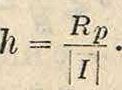
Напряжения E_lt возникающие на клеммах каждой пупиновской катушки, обусловливают в конце линии токи одной и той же частоты, которые складываются между собой. Принимая во внимание, что сила тока в п-м звене пупинизированной линии равна т _ v_t .-Μη-0,δ) ^п Zo ^е

где у_г=β_χ + га_г—постоянная распространения основной частоты на участке линии S между пупиновскими катушками, получим для напряжения в конце линии благодаря третьей гармонике перед п-й катушкой следующее выражение:

E_s =0,6 h

IVjl» e

Zoi

(- 2ft - 3iai) (n - 0,5) - Уз (IV—η)

1+e

где y₃=β₃ + га₃—постоянная распространения третьей гармоники, а N—число звеньев пупинизированной линии. Приближенно можем положить: β₃=β₁ и а₃=Зау, тогда после суммирования от п= 1 до η^Ν полу чим:

уг

-βχΝ

|Ζ„Γ ft

(E

Принимая во внимание, что β_χΝ равно всему затуханию b пупинизированной линии, получим т. н. коэф. «дребезжания»F (Klirr-faktor), то есть отношение амплитуд третьей и основной гармоники

M,3feg,₂f(l —е-^ь).

Для пупинизирования линии в среднем имеем: h sc 1000 Ω/Α; Z„=1 600; Ь=1,3; JST=70 Сдля участка линии между усилителями); V, =5 V; тогда

Чпат

Выбор собственной частоты /₀=~ пупинизированной л и н и и.

Для определения собственной частоты f₀ пупинизированной линии обратимся к ур-шо для километрич. затухания:

Rn -Ь Rj) т /* с

² у r_s +

Перепишем это ур-ие следующим образом:

8 =

¹ 2Z

Ei-»;²

+ ^{Rk т} 2Z

3 ,. Л к

--к+ А»· /------ ·

Ei-»;² 2 Ei-»)²

(10)

В спектре передаваемых частот желательно чтобы затухание как можно меньше зависело от частоты. Выясним, в какой мере может пупинизированный кабель удовлетворить этому требованию. Первый и третий члены ур-ия (10) увеличиваются при увеличении частоты; что же касается второго члена, то он имеет минимум при ч=0,7; сле-

довательно, если например »;= ——=0,7, то вплоть до=2 400 пер/ск. второй член уменьшается и компенсирует в возможной степени увеличение затухания, вызываемое первым и третьим членами. Т. к. для коммерческого телефонного разговора спектр частот сверху может быть ограничен f=2 400,

то /о=ηργ=3410 пер/ск., или ω„=21 400;

если эту величину для ω₀ принять для основной двухпроводной линии, то для четырехпроводной искусственной линии:

при «Д. Μ.»: ω₀₍₄₎=1,24 х 21 430=27 500;

при «Д. Зв.»: а>₀₍₁₎=1,66 х 21 400=35 500.

Из табл. 4 видно, что например при £>=1,7 км •телефонирование по двухпроводной линии ограничено искажением второго рода до 2 200 км, а по искусственной—до 4 500 км («Д. М.») и 6 000 км («Д. Зв.»); фактически эти расстояния приходится .уменьшать вследствие обратной связи в усилителях и явления подслушивания (смотрите Телефонная передача и Усилитель). Если желательно дальность телефонирования увеличить, то можно или применить скрещенные контуры или же увеличить собственную частоту пу-пинизированной линии; в последнем случае линия называется слабопупинизирован-ной в отличие от среднепупинизированной линии, для которой собственная круговая частота двухпроводной линии равна в среднем ω_ο=20 000. В настоящее время применяются следующие «степени» П.

1) средняя Π.: ω₀(₂>=20 000 ~ 21 400

2) слабая П.: ю₀₍₂₎=33 000-Е48 000

3) весьма слабая П.: а>₀₍₂₎=63 000-^82 000 (для передачи широковещания). В табл. 5 приведены примеры П. кабельной линии.

Пупиновекие катушки со времени их введения в эксплуатю претерпели до настоящего времени целый ряд видоизменений. При конструировании первоначальных образцов все усилия были обращены к тому, чтобы уменьшить омич, сопротивление обмоток, иначе говоря—повысить постоянную времени т, т. к., особенно при кабельных жилах большого диаметра, введение омич, сопротивления в линию может свести нанет уменьшение затухания, достигаемое увеличением самоиндукции, причем сразу же стало ясно, что наиболее подходящей формой сердечника катушки является тороидальная форма. Материалом для сердечника сперва предназначалось мягкое железо в виде тонких пластин. Но вследствие больших потерь, обусловливаемых такой конструкцией сердечника, от него пришлось отказаться. После долгих испытаний остановились на сплаве железа с силицием при толщине пластин 0,03 миллиметров, достигнув ; такими сердечниками удовлетворительных результатов. Каждая катушка имела две i обмотки для включения в оба провода линии. Такими катушками была оборудована в 1908 году первая подземная кабельная линия в Германии между Берлином и Потсдамом (40 км). Т. о. первый тип сердечника пу-пиновской катушки был сердечником из пластин. Но скоро были предъявлены новые требования к катушкам, именно когда в 1909 году Эбе линг указал путь для более рационального использования жил кабеля в виде четырехпроводной искусственной линии. Катушка с сердечником из пластин оказалась неподходящей для включения в искусственную и основные линии, т. к. потребовалась бблыдая магнитная стабильность; поэтому остановились на проволоке диам. 0,15 миллиметров из следующего сплава: 3,7% Si; 0,06% С; 0,31% Мп; 0,013% Р;0,14% S;0,065% Си. Катушка с таким сердечником при пропускании через ее обмотки тока силою 200 тА изменяла свою самоиндукцию не более, чем на 2%, в то время как катушка первого типа при пропускании через ее обмотку тока силой 50 тА изменяла свою самоиндукцию более, чем на 5%. Кроме того потери в железе благодаря большему подразделению егопо сравнению с пластинчатым сердечником значительно снизились. Такими катушками (2-го типа) оборудована кабельная линия между Берлином и Рейнской областью. С введе-ниемпромежуточныхуси-лителей благодаря возможности применения кабельных жил более тонкого диам. пришлось в третий раз изменить тип сердечника пупиновской катушки. С одной стороны, стало возможным несколько снизить постоянную времени катушки (с г=0,03 дот=0,014), но, с другой стороны, возросли требования к сердечнику. Мы уже знаем, как влияет изменение самоиндукции кабеля на волновое сопротивление линии, и знаем те требования, какие должен быть предъявлены к равномерности самоиндукции катушек. Этим требованиям катушки с проволочными сердечниками не удовлетворяют. Необходимо иметь катушки, самоиндукция которых отличается еще большим постоянством. Для этой цели был .применен сердечник из прессованного порошкообразного железа, зерна которого имеют такой размер, что проходят через сито, имеющее 10 000 отверстий на 1 см². Этот порошок перемешивается с изолирующей массой, благодаря чему каждое зерно железа обволакивается изолирующим слоем; затем этой тестообразной.

Таблица 5.—С пссобы П. кабельных линий.

Наименование линий	Диам. шил, миллиметров	о 3	Затухание на 1 км при ω=5 000	Волновое сопротив ление	Расстояние между катушками S	Самоинд. катушки Ls		Приме чание
Реннский кабель	3	19 000	0,00314	1 340	1,7	0,15
» »	2	16 500	0,0050	2 150	1,7	0,24
Норм. нем. ка-
бель, двухпро-
водная линия.	1,4	16 700	0,0С96	1 600	2	0,19
Искусственная
линия.	1 ,4	21 600	0,0097	760	2	0,07		Средняя
Двухпроводная								пупини-
линия.	0,9	16 800	0,0189	1 680	2	0,20		зация
Искусственная
линия.	0.9	22 200	0,0196	790	2	0,07
Двухпроводная
линия.	0,9	33 500	0,083	860	2	0,05		Слабая
Искусственная						>		пупини-
линия.	0.9	43 000	0,032	440	2	0,02 J		зация
Двухпроводная
линия.	1,4	21 400	0,0093	1 520	1,7	0,14
Искусственная
линия.	1,4	27 000	0,0093	760	1,7	0,056		Средняя
Двухпроводная								пупини-
линия.	0,9	22 500	0,0195	1 570	1,7	0,14		зация
Искусственная
линия. Ϊ	0,9	28 000	0,0190	780	1,7	0,056

Фигура 14.

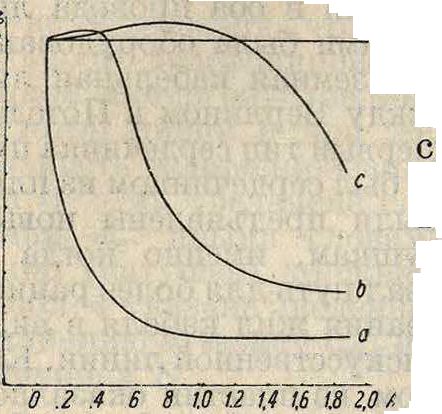
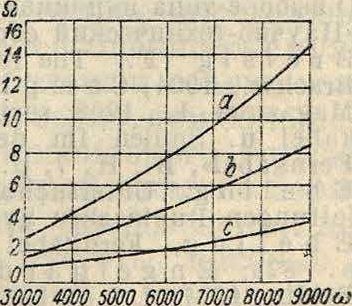
массе придают желаемую форму под прессом. Изготовленные таким образом сердечники выдерживают на изгиб 2 килограмма!мм². На фигуре 14,15 и 16 даны сравни-d тельные данные, характеризующие пу-пиновские катушки различными сердечниками. (На фигуре 14 дана зависимость потерь в железе от ω для различных типов сердечника: а—из пластин, 6— из проволок, с—из

Фигура 15. прессованного по рошка. На фигуре 15—

изменение самоиндукции в зависимости от постоянного тока после предварительного намагничивания: а — сердечник из пластин, Ь—из желез- % ной проволоки, с— ²

из проволоки, пред- & _гставляющей сплав | ₄железа с силицием, I в d—из прессованно- | * го порошка. Фигура 5 ®

16 — изменение са- 1 _пмоиндукции в за- | » висимости от силы з тока: значения а,

Ь, с d те же, что и на фигуре 15; измерение самоиндукции производится при наличии тока в катушке.) Катушки помещаются в специальном ящике (фигура 17), размеры которого конечно различны и зависят от числа катушек,

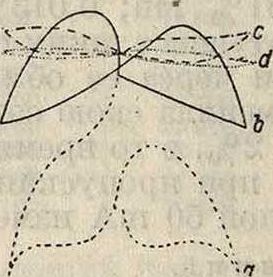
ВО 64 40 20 0 го 40 SO 80 тонн В

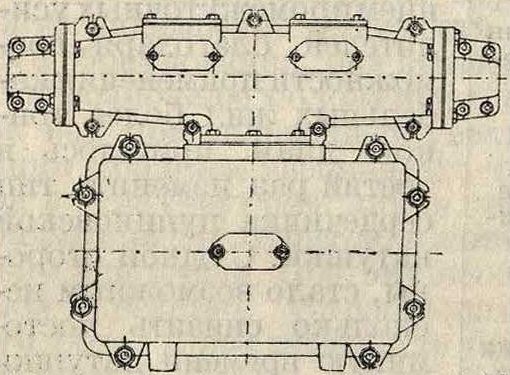
Фигура 17.

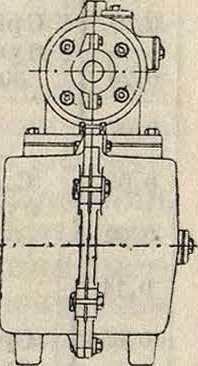
требуемых той или иной конструкцией кабеля. Перед помещением в ящик катушки заключаются в цинковую, наглухо запаянную коробку. В табл. 2 приведены электрич. данные употребляемых катушек.

Лит.: Юрьев М. Ю., Телефонирование по кабелю на далекое расстояние, М., 1927; его же, Первый пуиинизированный кабель в СССР, «Научно-технический сборник НКПиТ», М., 1929, 4—а; его ж е, Теория телефонной передачи, М., 1931; его же, Теория, телефонных цепей, Москва, 1925; его же, О выборе типа пупянизированного кабеля для СССР, «Научно-технический сборник НКПиТ», М., 1928, 1; В г e i s i g Г., The retische Telegraphie, 2 Aufl., Brschw., 1924; Campbell A., «The Philosophical Magazine», L., 1903, series 6; D о h m e η K., Fern-babel u. Spulen im deutschen Fernkabelnetz, «Das Fernkabel», В., H. 7, p. 28; Dolezalek F. und E b e 1 i n g, Untersuchungen liber telephonische Fern-leitungen Pupinschen Systems, «ETZ», 1910, p. 1059; E b e 1 i n g, Fernkabel u. Verstarkung, ibid., 1921, p. 873; Engelhardt V., Fernkabeltelephonie, Berlin, 1927; Llischen P., Berechnung von Fern-spreehleitungen, «Telegraphen- u. Fernspreehtechnik», B., 1919, p. 81; L· u s c h e η P., Ueber die Berechnung v. Pupin-,Doppel- undViererleitungen,ibid.,1918,p, 185; «ETZ», 1923, p. 35; F υ n d i 1 I e r W. u. Martin W. H., Hysteresis Effects with Varying Superposed llagnetising Forces, «JAIEE», 1921, p. 443; Speed

and ElmenS. W., Magnetic Properties of Compressed Powdered, ibid., 1921, p. 596; Ehlers W., Puplnspulen mit Massekernen, «Elektrische Nachrlch-tentechnik», B., 1925, H. 5, p. 121; Ehlers V. u. Falkenberg F., Ueber die Wirkung desPress-drucks auf die Eigenschaiten v,.n Massekernen fiir Pupinspulen, ibid., 1926, p. 281; Heaviside 0., Electromagnetic Theory, v. 1, p. 445, L., 1922; P u-p i η Ы. K., «Transactions of the American Institute of Electric. Eng.», v. 17, p. 445; Campbell A., «The Philosophical Magazine», 1903, v. 5, series 6,. p. 313; E b e 1 i n g, «ΕΤΖ», 1907; Gherardi, «Trans, of the Ameiican Institute of Electric. Eng.», 1911, v. 30, p. 1743; Jordan, «ΕΤΖ», 1918, p. 61; Wagner K.W., «Archiv fiir Elektr.», B., 1919,v.8, p. 62; Carson J., «Trans, of the American Institute of Electrie. Eng.», N. Y., 1918, p. 345; Meyer, «Ztschr. fiir techn. Ihysik», Lpz., 1921, v. 2, p. 306; Kiipfmiiller K., «Telegraphen Fernsprechtech-nlk», B., 1922, p. 45; L (1 s c h e n F. u. K ii p f m ii 1-ler K., «Eur .paischer Fernsprechdienst», B., 1927, v. 4, p. 10; Klein M., Kabeltechnik. Die Theorie, Berechnung u. Herstellung d. elektrischen Kabels,. 1929; Compte rendu des travaux de l’assembiee р]ё-nidre du Comite Consultatif International des communications teldphouiques a grande distance, P., 1910, t. 4; Winzheimer R., Ueber Tragungstechnik, Mch., 1929; H i 1 J. C., Ea transmission te]6nboni-que, P., 1924. M. Юрьев.