Работа

Работа есть количественная мера изменения форм движения материи (Энгельс). Реальные процессы неизбежно сопровождаются постоянным изменением форм движения (превращение одних видов энергии в другие) и следовательно постоянно совершается работа. В идеализированных образах теоретич. механики простейшая форма движения—механич. перемещение тел в пространстве—может оставаться неизменно таковым (инерционное движение, равномерное вращение по кругу), причем работа не производится в соответствии с данным выше определением. Энергия м. б. определена, как способность совершить Р. В абстрактной схеме механики может существовать движение, не сопровождающееся изменением формы и следовательно может существовать энергия, не производящая Р. В действительных процессах природы энергия всегда соответствует движениям с меняющимися формами и тем самым энергия всегда является мерой движения при изменении формы последнего (Энгельс). Принцип неразрушимости движения, находящий конкретное и наиболее общее выражение в законе сохранения энергии, м. б. выражен (как показывает опыт) при переводе различных форм движения в механическую,

mv²

как инвариантность произведения - (для случая «точки» с массой т и скоростью v). Отсюда совершенная Р. определяется как разность У¹ ^^Vi~ ^v‘^>- (v_L, υ., — начальная и конечная скорости). При выборе другой фюрмы движения (тепловой,электрической и т. д.) в качестве стандарта определение Р. соответственно изменилось бы по внешнему виду, оставаясь прежним по существу. Исторически понятие Р. возникло как вспомогательное, вторичное понятие, определяемое в ньютоновской механике через понятие силы. Элементарной Р. силы F называется скалярное произведение век тора силы на вектор пути, причем это определение формально совпадает с данным выше и имеет всеобщее практическое распространение. Поэтому в дальнейшем изложение ведется на основе этого общепринятого определения.

Если точка переместилась на величину df под действием силы F, то энергия, приобретенная телом, т. e. Р. силы F:

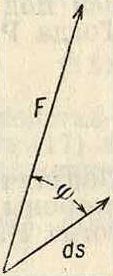
A=F Λγ — F ds cos φ (1)

или в координатах

А —X dx+Y dy+Ζ dz, (2)

где F и ds—длины векторов F и dφ—угол между ними (фигура 1), а X, Υ,Ζ и dx, dy, di—проекции этих векторов. Из (1) видно, что Р. отрицатель-

Л ^

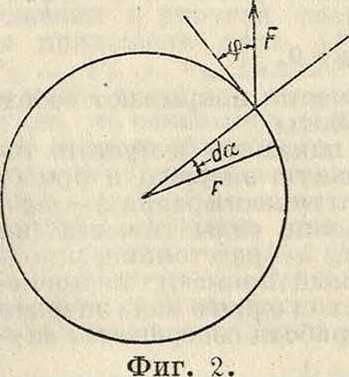
на, если φ > ~ · В механике нередко пользуются и другими системами координат, наир, полярной; тогда вместо (2) получаются другие выражения. Однако всякое выражение работы имеет размерность энергии (смотрите Размерность), так как работа и есть, согласно приведенному определению, энергия.Например при вращении точки по окружности (фигура 2) работа силы F будет

FdrF · г cos φ d<p=М d<p, (3) Фигура 1.

где М—момент силы, имеющий размерность силах длина, а άφ—величина нулевой размерности, тогда как все произведение имеет прежнюю размерность. Если точка движется по инерции, встречая сопротивление/, всегда, как известно, направленное против движения, то cos φ равен -1 и работа отрицательна: энергия, запасенная в точке в виде кинетической энергии, убывает. Для подсчета Р. силы на пути конечной длины складывают Р. на отдельных элементах пути; это следует делать на основании закона сохранения энергии. Согласно этому имеем:

Ь Ь

Λah — s FI ds, cos φ-~ J (X dx + Y dy + Z dz), (4>

a a

где интеграл берется по пути перемещения точки от начального положения а до конечного b (фигура 3). В ме

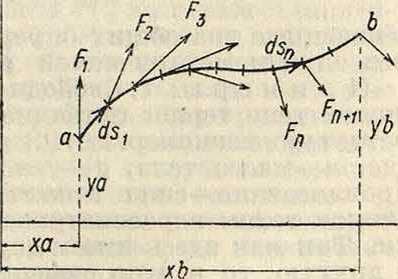
ханике доказывается, что в случае, если сила, действующая на точку, есть градиент скалярного потенциала, то есть удовлетворяет условию:

F=νφ, (5) то работа силы на пути аb не зависит от формы пути, но определяется целиком положением начальной и конечной точек пути. Рассмотрим теперь систему двух точек, связанных теми или иными силами (например положительный и отрицательный электроны, земля и луна). В различных фазах движения система эта обладает одною и тою же полной, но различными количествами частного вида энергии: например в простейшем случае колебания по прямой положительного и отрицательного зарядов при их наибольшем удалении кинетич. энергия системы равна нулю (обе точки неподвижны в этот момент) (фигура 4), а потенциальная имеет максимум;когда обе ? о о точки окажутся в поло-

-^т-¹-^ жении О, кинетич. энер-

⁺ гия достигнет максималь-Фигура 4. ного значения, потенци альная же упадет до нуля (точнее—до минимальной своей величины); следовательно при изменении конфигурации (геометрич. расположения частей) системы один вид энергии переходит в другой, то есть совершается внутренняя работа; для ее подсчета достаточно сложить Р. силы, действующей со стороны точки а на точку Ь, рассматривая эту силу как внешнюю по отношению к точке b, и Р. силы, действующей со стороны точки b на точку а; математически это выразим так:

А=F_ab dsj) + Fba · ds_a, (6)

где F_ab—сила, действующая на точку b, и F/,_a—сила, действующая со стороны точки b на точку а. Согласно закону равенства действия и противодействия F_a&==-Fba- Заметим, что если работа положительна, то кинетическая энергия системы увеличивается, что видно например из фигура 4: для точки а Р. положительная и кинетическая энергия увеличивается; то же и для точки b. Вообще положительная Р. внутренних механич. сил увеличивает кинетич. энергию системы, отрицательна я—у величивает потенциальную энергию. Два разобранных примера показывают, как вычисляется внешняя и внутренняя Р. л в самом общем случае механики системы точек. Назовем через Fi силы, действующие на точки системы со стороны тел, к системе не принадлежащих; через dFi—бесконечно малые перемещения точек под действием этих сил, через п—число точек. Тогда Р. внешних сил

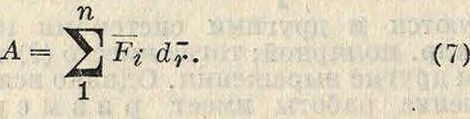
Обозначим далее через F_?;/_f силу, действующую со стороны точки, обозначенной номером г, на точку к; тогда Р. внутренних сил

причем суммирование распространено на все возможные комбинации знаков г и к кроме случая их равенства. Выражение п

2 м

есть очевидно сила, действующая со стороны всех точек системы на точку к, точнее ее компонента по направлению пути. Отсюдавидно, что сумма не должна содержать F*#, так как силы, действующей от точки к на нее самое, нет. Вместо того чтобы упоминать о необходимости вычеркивать члены с равными значками, достаточно поставить—вообще необходимое—условие соблюдения закона равенства действия и противодействия:

Ftk — — Fjd, (9)

т. к. отсюда следует, что

Fkk=~F_kk=0.

Указанные два общих определения покрывают собою все случаи механической работы.

Примеры: 1. Свободно падающее в пустоте тяжелое тело теряет потенциальную энергию и приобретает кинетич. энергию. Р.силы тяжести равна A=mgh, где т—масса тела, д—ускорение силы тяжести (их произведение—сила тяжести), h—расстояние, пройденное телом в рассматриваемый промежуток времени. Так как здесь имеем переход одного вида энергии в другую, то в этом смысле работа совершается внутренней силой.

2. Если свободно падающее тело находится в жидкости, то вследствие сопротивления среды оно через лек-рое время после начала движения начинает двигаться равномерно, т. к. сила тяжести уравновешивается силой сопротивления, направленной п р о т и в движения. Здесь работа будет ! FI · |ds| cos (F, ds)=H F| ·! de|, следовательно тело теряет энергию. В самом деле, опускаясь, оно теряет потенциальную энер м

Фигура 5.

л:

гию, но кинетическая энергия не увеличивается, так как скорость постоянна.

3. Трактор тянет груз с силой F, и движение равномерно. Если мы мысленно обрежем груз и заменим его силой, то, как в предыдущем случае, cos (F, ds)==— 1, и трактор теряет энергию, совершая Р.

4. Двигатель А (фигура 5) при помощи пр^одного ремня вращает машину В. Мысленно разрезав ремень в точке М и заменив его натяжение силой F, имеем снов, cos (F, ds)=-i, таким обр. мотор совершает Р.

5. Сжатая пружина внезапно освобождается. За счет работы внутренних сил ее потенциальная энергия начинает переходить в кинетическую.

6. Газ расширяется (весьма медленно) вследствие нагревания и подымает поршень на высоту c?/i. Если давление па поршень есть Р (фигура 6), то сила, давящая на газ, есть PS (S — площадь сечения поршня), работа отрицательна и равна PS · dh=Р dv, где dv — изменение объёма; газ, совершая работу, теряет свою энергию.

7. Р. электростатич. и магнитных сил ничем по существу от механической не отличается и все приведенные формулы применимы и к этому случаю.

8. Р. электрич. тока см. Топ электрический.

Лит.: Жуковский Η. Е., Аналитическая механика, М.—Л., 1925; Гримзель Э., Курс физики, пер. с нем., т. 1, ч. 1, 4 изд., М.—Л., 1931; И о ф ф е А. Ф., Курс физики, ч. 1, 3 изд., М.—Л., 1931; Энгельс Ф., Диалектика природы, статья: «Мера движения—работа». Н. Андреев.