> Техника, страница 75 > Работа упругих сил

Работа упругих сил

Работа упругих сил, работа сил упругих деформаций. Пусть имеется упругая система, следующая закону Гука (смотрите Сопротивление материалов), свободно опирающаяся на две опоры и подвергающаяся воздействию внешних сил Р_г, Р_г,., Р_п. Допустим далее, что точки приложения этих сил под действием последних перемещаются по направлениям линии действия сил на расстояния, соответственно равныеs_lt s₂, ., s_n.

Фигура б. воздействия на систему возрастают до конечных своих размеров сравнительно медленно, то работа этих сил при деформировании системы до предела упругости последней будет аккумулироваться в ней в виде потенциальной энергии, которая вновь проявится в виде соответствующего количества кинетич. энергии, как только рассматриваемые внешние силы прекратят свое действие.

Работа, совершаемая упругой системой, и называется работою сил упругих деформаций. Из вышесказанного следует, что Р. у. с. определяется величиной работы внешних сил, деформировавших упругую систему и обусловивших в последней наличие определенного запаса потенциальной энергии. Поэтому исследование вопроса о Р. у. с. сводится к исследованию вопроса о потенциальной энергии деформации упругой системы.

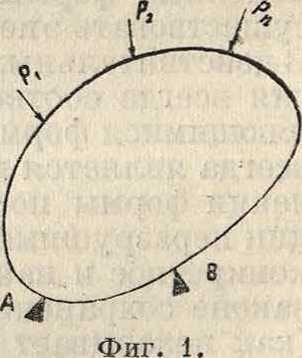
Пусть имеется упругая плоская система, находящаяся под действием внешних сил P_lt Р₂, .,Р»-_еи свободно опирающаяся на опоры А и В (фигура 1). Допустим, что силы Р], Р₂, ···, Рп переменны по величине и возрастают до своих конечных размеров сравнительно медленно, т. ч. динамич. влияния их на упругую систему не сказываются. Рассмотрим в дальнейшем тот частный случай, когда силы Р_г·, возрастая, сохраняют одни и те же отношения. Если материал системы подчиняется закону Гука и если деформация системы не выходит за. предел упругости материала, то существует прямая пропорциональная зависимость между силою Р_г· и соответствующим смещением si

точки приложения силы Р_г· по направлению последней, так что

Р*=As“, (г =1,2, В, ., η), (1)

где А—определенный коэфициент пропорциональности, определяемый свойствами материала упругой системы. Элементарная работа силы Р» при этом (смотрите Работа)·.

dTi=Р idsi As ids{, (2)

а полная работа при изменении s* от 0 до s*

^si

Т J Pid₄=j

•г — б

δί=0

As_?;ds_z=Я -^·

или, так как по равенству (1) то согласно (3) и (4)

_r._^Pi^si ¹ 2

(3)

(4)

(5)

Работа же всех сил, равная накопленной упругой системой потенциальной энергии U, выражается так:

Согласно (1)

^,;i2^ps

г 1

(в)

(7)

вставляя (7) в (6), получаем так же:

г=1 г= 1

Т. о. потенциальная энергия, накопившаяся в упругой системе, как видно из равенства (8), есть однородная квадратная ф-ия внешних сил, действующих на систему. Если, наоборот, в равенство (6) вставить значение Pi, определяемое из (1), то п

^42w-i-2

(9)

г-1

Т. о., как видно из последнего равенства, потенциальная энергия, аккумулированная в упругой системе, есть также однородная квадратная ф-ия смещений точек приложения действующих сил по направлениям действия последних. Этими же свойствами очевидно обладает и работа сил упругих деформаций системы при переходе потенциальной энергии системы в кинетическую. Что же касается реакций опор А и Б, то работа этих двух сил равна нулю, т. к. точки приложения этих сил оставались неподвижными; величины же этих реакций легко определить, исходя из статических условий равновесия (смотрите Механика теоретическая).

В случае, если имеется статически неопределимая система, то действия опор должен быть заменены соответствующими силами реакций R{, работа которых при деформации системы вообще не будет равна нулю, т. ч. правая часть равенства (6) будет содержать члены, зависящие не только^от сил Р_г·, но и от сил реакций Р*·. Пусть к упругой системе вместо сил Р_г· приложен ряд л ар сил, величины моментов которых пусть будут М_г, М₂, ., М_п, причем соответствующие углы закручивания пусть будут ψι, <Р2, ., φ._η. Нетрудно устано-вить, что зависимости, установленные выше между величинами Р_?; и s*·, существуют также и между величинами Mi и (fi. Пусть например к одному из оснований упругого цилиндра, закрепленного другим своим основанием, приложена вращающая пара, момент которой равен Mi- Между М_г· и углом закручивания цилиндра существует линейная зависимость:

Mi=pq>i. (10)

Элементарная работа <1Т_г- рассматриваемой пары при угле закручивания, равном d<p_z, равна произведению Mi на £%, так что

dTi=Mid<Pi. (И)

Полная же работа Т пары при изменении <р₇ от 0 до т выражается так:

Ψί <Р

Тг=J* M{dq>i=μ J nd<Pi=f (¹²)

Ч>%=0 <Pi=0

или, принимая во внимание равенство (10),

Ti= ₂ MiVi.

(13)

ЗЕ-сли приложены п вращающих пар, то потенциаль-адая энергия U* упругой системы

V=2 П=I 2 Мт.

(14)

г=1

Принимая во внимание соотношение (10), получаем и в рассматриваемом случае, аналогично равенствам <S) и (9), равенства:

(15)

(16)

Вследствие аналогии между величинами Pi и М*·, с одной стороны, и величинами s* и <pi—с другой, аналогии, проявляющейся и во многих других случаях, часто понятью силы придают более общий, чем обычно, смысл, подразумевая под термином «сила» не только обычное понятие о ней, но и пару сил, а также совокупность двух равных и противоположных сил, имеющих одну и ту же линию действия и тому подобное. В таких случаях говорят об «обобщенной силе». Т. к. на данную упругую систему могут действовать одновременно обобщенные силы различных типов, то, принимая во внимание аналогию ф-л (8) и (9) с ф-лами (15) и (16), можно вышеприведенные положения обобщить след, обр.: потенциальная энергия упругой системы, подчиняющейся закону у -

"-----V~----тЬ

Гука и подвергающейся воздействию каких угодно обобщенных сил, есть однородная квадратная функция этих сил.Н апример пусть

Фигура 2.

имеется балка, изгибаемая силою Р, приложенной к ее середине, и парой М (фигура 2). Стрела прогиба <5 и угол а согласно выводам сопротивления материалов выражаются следующими равенствами:

. is _п L2

Р + ттг^М, (17)

48 EI

12

16EI ‘ l

ЮЕ1^{Р +} Ш^М-

(18)

Придавая формуле (6) обобщенный смысл, то есть подставляя в нее вместо s*· значения δ и а из равенств (17) и (18), получаем для потенциальной энергии выражение

U=-

12 12. ,48Ё7^{Р +} 16Я7^М)

М I га г

2 (l6E/^{P +} 3EI^M)

(19)

Правая часть последнего равенства и представляет собой однородную квадратную ф-ию обобщенных сил Р и М. Решая совместно уравнения (17) и (18) относительно Р и М и подставляя найденные значения их в уравнение (19), найдем, что U есть также однородная квадратная ф-ия смещений <5 и а, которые поэтому носят название «обобщенных смещений».

Пусть при указанных выше условиях к данной упругой системе приложены обобщенные силы P_ltР 2> ···, Pi у Рп> так что

U-HPu Рг, ·.·, Р_п), (20)

и пусть какая-либо из этих сил, например Р₇, -увеличивается на бесконечно малую величину dP_?·. Потенциальная энергия системы, равная работе сил Р₂, Р₂,., Р_г-+ + dP₇, ., Р_п очевидно равна

^u+w;^ip‘·

(21)

Последняя величина потенциальной энергии системы очевидно не зависит от порядка следования друг за другом рассматриваемых сил в процессе их приложения к упругой системе. Допустим, что сначала приложена сила с£Р_г·, а затем лишь силы Р, Р₂,Р_г·,Р_п- Так как сила dPi вызывает бесконечно малое смещение, то работа dP*· при этом смещении будет, на основании вышесказанного, бесконечно малой величиной второго порядка малости, которою вследствие этого и можно пренебречь.При приложении затем сил Р_1г Р₂,., Рг, ., Рп они совершают работу, равную U, и кроме того сила dP* совершает еще работу, равную <5i dPi, обусловленную смещением ό_ζ·, вызванным силою Р“. Следовательно потенциальную энергию системы можно с точностью до бесконечно малых второго порядка выразить так:

U + didPi. (22)

Из сравнения сумм (21) и (22) следует, что

*-&·

Последнее равенство показывает, что если потенциальная энергия упругих деформаций системы м. б. представлена как однородная квадратная ф-ия при-

ложенных к системе обобщенных сил. то частная производная потенциальной энергии системы по какой-либо из этих сил равняется обобщенному смещению, вызванному этой же силой. Это предложение носит название теоремы Кастильяно. Вышеприведенный пример подтверждает справедливость этой теоремы. Так, беря частную производную по Р от (19), имеем, принимая во внимание (17):

дР 48EI^{Р Ь} 16Е1 ^{м 1}

Точно так же, беря частную производную от (19) по М, имеем, принимая во внимание (18):

¹ _т М ~ а. (95)

дМ 16 EI 3 EI

Пусть далее имеется статически неопределимая система с определенным числом излишних закреплений. Заменив эти закрепления соответствующими силами реакций й_ь Н₂,., К_я> допустим, что закрепления таковы, что перемещения точек приложения сил й,· невозможны по направлению последних. Тогда на основании теоремы Кастильяно имеем:

dU_

Эй,

= 0;

9U

ад₂

= 0;

OU

ад»

= 0.

(26)

Т.к. число неизвестных R^R ₂,., Д„, равно числу ур-ий системы (26), то, решив последнюю систему, можно найти и значения этих неизвестных. Так как U должен быть однородной квадратной ф-ией от Д, Н₂, ., Н», то

+ Пгз Дг Дз +. + &пп Rn>

(27)

где Он, а₂2, ···, о,2, .—нек-рые коэф-ты. В виду того, чтоЕ7>0 при всех значениях Д_1; Д₂, ., Д», то из (27)

следует, что все коэфициенты ay (i=1, 2.п; 3=1,

2,. ,п) д.б. положительны. Взяв вторые производные по Д, Д₂,. Д„ от ?7, имеем из (27):

аги gzu

—я=2ац; —з=2а₂23 ··· дЩ дЩ

aw

эд!

= 2а.цп· (28)

Отсюда следует, что вторые производные функции U по К, Д₂, ., R_n положительны. Наличие последнего обстоятельства вместе с наличием системы ур-ий (26) представляет условие для минимума функции U. Таким образом определение излишних неизвестных сил д_х, д₂.Д_и статически неопределимой системы при помощи системы ур-ий (26) сводится к подысканию для К, Д₂,. Д« таких значений, при которых значе-А и (в ние потенциальной энергии системы становится минном мумом. Это и есть так называемым начало наименьшей работы.

В качестве примера рассмотрим следующий случай. Пусть имеется неразрезная балка, нагруженная равномерно распределенной нагрузкой q и имеющая три опоры (фигура 3), реакции которых суть h, В и M, направленные вертикально снизу вверх. Взяв алгебраические суммы моментов всех сил, приложенных к балке, сначала относительно точки М, а затем относительно точки Я, и приравняв эти суммы нулю, получаем:

_A=ii±b__Bb)

* ^а+Ь (29)

Потенциальная энергия изогнутого стержня согласно выводам сопротивления материалов получает выражение

q(a*b)

Фигура 3.

r₁₌JL Г

¹ 2Е 1,1

М* dx,

(30)

^T=djf {^Ах «f

о

“2ΕΪ (

, „as a<, „ αΛ

AS— -Aq — + q2~J·

Потенциальная энергия Т2 правого пролета получается аналогичным образом:

^Т*=ш{^в2т-^в«т⁺^)·

Т. о. вся потенциальная энергия Т стержня

^т~^:т>^+т>=ш{^А‘т~^А«т^{+<! а}‘

Производная от Т по R из последнего равенства

20

_ Ьз Ь⁴

+ B2—~Bq — -3 4

(33)

(34>

ΘΓ 1 Г i «³ a‘ dA

- дД~2й[ 1^2А 3 ⁹ 4) £ίΐΓ

+

Из равенств (29)

_п Ьз Ь* dBl (^2В 3 ®.4 ) dR J

dA

dR ° dB dR ‘

(35>

(36)

(3 7)

a + b

Подставляя значения (36) и (37) в (35) и принимая во-

дТ а внимание,что при неподвижности средней опоры—=О, .получаем после ряда преобразований, что

R=—^-г (аз + 4а2Ь -ь 4аЬ2 4-Sab

При равных пролетах, то есть при а= b

т> ⁵

R=~aq.

b з). (38>

где М — изгибающий момент для левого пролета, равный

М=Аж-?|². (31)

В рассматриваемом случае потенциальная энергия Τι левого пролета

(39>

Пусть имеется упругая система, подвергающаяся воздействию со стороны двух различных систем нагрузок, СОСТОЯЩИХ ИЗ СИЛ Р_1? Р2, Рг “ СИЛ Pf+1, Pi+2, ., Р_п. Что же касается опор, то допустим, что они м. б. определены из уравнений статики или, в случае статич. неопределимой системы, что излишние закрепления заменены соответствующими излишними силами реакций. Пусть далее под действием первой системы сил точки приложения всех сил смещаются по направлениям последних на расстояния <5_г,<5₂, ., δ,;, <5_г-₊₁, ., δ_η, а под действием второй системы сил— на расстояния <5_Ь <5₂, <5_г·, <5_г+1, ., δ_η. Желая опре делить потенциальную энергию всей упругой системы под действием всех сил Pi, Р₂,., Рг, Р?;+1, · · · > ^рп> допустим, что сначала действовал лишь первый вид нагрузки. Тогда потенциальная энергия системы выражается на основании равенства (5) суммой

Ρ δ_τ Ροδο, РА

2 2 ^ 2

Прилагая затем вторую группу сил, получим следующее выражение для потенциальной энергии системы от действия этих сил

2

, Рг+2^г+2.. Ρηδη

Кроме того под действием 2-й группы сил точки приложения 1-й группы сместятся по направлениям последних сил на <5_Ь до, ., δ,;, т. ч. эти силы совершают работу, равную

Ριδι + Р-А+ .+ ΡΐδΙ

Следовательно упругая система под одновременным действием сил обеих групп будет обладать потенциальной энергией и=-Рг₊Фг.

-¹ + -

Р%1

^:+-

+-

Ρηδη

, РА, Рг+1 δ{~, 2 ‘ 2

+ Ρι<5ι + · · ·+ Ρφ%.

(40>

2 2 С другой стороны, прилагая сначала 2-ю группу сил, а затем 1-ю группу и рассуждая так -же как в первом случае, получаем

U — Pf+^i+i Рг+2^г+2 _

·+-

ρ_Λδ

+ ^1+.

+ Р г+ify+i + *

(32)

2

РА

• + -у- f Ч+Ши Сравнивая (40) и (41), имеем:

Pi<5j + Р2^2 + ·. · -f Рг^г ⁼ РId-Ai+i +

1^1

2

РА

+

+ Рг+2^г+2 + ·

PvAn

(4 1 >

(42>

то есть работа, произведенная силами первого состояния упругой системы при перемещениях второго ее состояния по направлениям сил первого состояния равняется работе сил второго состояния этой же упругой системы при перемещениях первого ее состояния по направлениям сил второго состояния. Это

предложение и составляет т. н. теорему о взаимности перемещений (смотрите); она часто применяется при решении вопросов, связанных со статически неопределимыми системами, подвергающимися воздействиях! каких-либо подвияшых нагрузок (при расчете кранов, мостов и тому подобное.).

О принципе возможных перемещений, или о принципе возможных (виртуальных) работ см. Механика теоретическая.

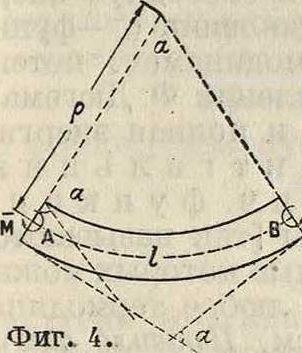
Изложенные выше теоретич. выводы имеют обширное практич. применение, например при расчетахпотенциальной энергии, накапливаемой при деформировании упругих брусов, пластин, пружин, при определении величин прогибов и углов наклона балок, рельс и тому подобное. с различными способами закрепления и видами нагрузок, при расчете изгиба рам, при динамич. исследовании явлений колебаний и вибраций и т. д. В качестве иллюстрации применения вышеприведенных теоретич. выводов рассмотрим следующие примеры. Пусть имеется призматич. стержень АВ, к концам которого приложены две равные и противоположные пары с моментами, равными M и -М (фигура 4), действующие в продольной плоскости, и симметрии стержня. В сопротивлении материалов напряженное состояние стержня при этих условиях получает название чистого изгиба. Если получаемый при этом изгиб не выходит за пределы упругих деформаций материала, то работа Τвнеш-них сил при этом будет равна

(43)

где а—угол наклона плоскости сечения одного конца балки относительно дру го го. Есл к I—длина балки до изгиба, равная длине нейтрального слоя балки после изгиба, то

i

α=,

в где ρ—радиус кривизны нейтрального слоя. Из равенств (43) и (44) получаем следующее выражение для работы Т внешних сил, приложенных к данной упругой системе или, что количественно то же самое, для потенциальной энергии U чистого изгиба:

T=U=f-· (45)

Так как далее е=ТП’ ί⁴⁶)

где Е—модуль упругости, а 1—момент инерции поперечного сечения балки относительно нейтральной оси, то

(⁴Л

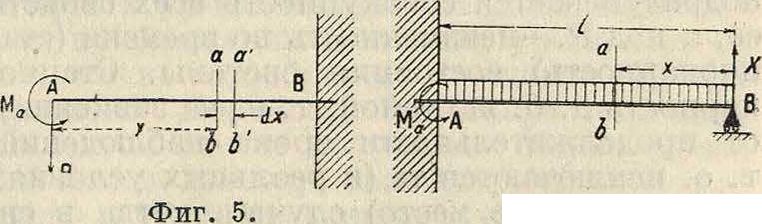
Пусть далее имеется консоль АВ (фигура 5), к концу А которой приложена сила Р и пара, момент которой М„. Для сечения аb, находящегося на расстоянии х от конца А балки, изгибающий момент

(44)

М=— Рх — М_а.

(48)

Потенциальная энергия dU изгиба элемента балки длиною Ах, следующего непосредственно за сечением аb, равна на основании формулы (47):

Проинтегрировав обе части последнего равенства в пределах от 0 до Ϊ, получим потенциальную энергию Ό изгиба всей балки.

U

О

М 2 dx 2 EI

(50)

dU =

Μ 2 dx 2ΕΙ

(49)

Пусть требуется определить прогиб рассматриваемой балки в точке А. Применяя теорему Кастильяно, имеем из (50) и (48)

_f=^aJL₌± f^MX^dx ₌ JL Г JL (Μη dx =

¹ дР дР J 2El 2EI J 6P^{KU L}

0 0 l

= 2Wrf ipl(Px+ M_aY]dx =

0

l

= (Px + M_a)xdx=^ + ^· (51) о

В качестве иллюстрации применения вышеизложенного начала наименьшей работырас-смотрим следующий пример. Пусть имеется балка постоянного сечения, один конец которой А заделан, а другой свободно опирается о подставку В (фигура 6), ипусть балка равномерно нагружена нагрузкою q. Обозначая опорную реакцию конца В балки через Х> а реактивную пару, препятствующую повороту сечения А балки через М_а, принимаем×за лишнюю неизвестную, каковую надлежит определить. Изгибающий момент Ж в сечении аb, отстоящем от В на расстоянии х,

М=Хх-⁹х (52)

Если пренебречь влиянием скалывающих сил, то потенциальная энергия изгиба стержня на основании (50) и (52)

_тг CM*dx с^{{Хх qx2)idx}

“~,!^ЁГ= J--ш--(°³>

о о

На основании начала наименьшей работы:

Ш=2ЕТ Ш [{^Хх - 2 m ^dx =

, ⁰ (54)

= ш f (^Хх -1 νή ^χάχ=Έϊ{^χτ-⁽1 τ) - °>

0

откуда

7С == I ql. (55)

Аналогичным образом м. б. определена и величина М_я. Начало наименьшей работы с большим успехом применяют для определе-

Фигура 6.

ния различных опорных реакций ферм, усилий в лишних стержнях и вообще для определения лишних неизвестных в упругих системах. Что касается теоремы о взаимных перемещениях, то при ее помощи легко разрешаются вопросы, связанные с расчетом неразрезных балок (смотрите Балки неразрезные), в частности определение реакций промежуточных опор этих балок; вообще теорема о взаимных перемещениях имеет весьма важ-

ное значение для теории статически неопределимых СИСТем. М. Серебренников.